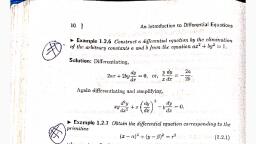Page 1 :
Examples X(C), , ; Find the orthogonal trajectories of the following families of curves (a, and c being the variable parameters):, , y” = 4az. (C.H. 1981], EY = a(x +a). [C.H. 2000], Z + Qy? =e,, , oye? y? —2ax = 0., “ED oy eto oo, , ANT = ad.

Page 2 :
Chapter 10. Geometrical and Physical Applications [ 413, , Tr = acos@., , , , , =a+cosnd,, , ~ Show that the orthogonal trajectories of (c,a, parameters), Lo the family of circles x? + y? — k? = 2cy is a? + y? +k? = Qe., the series of astroids 27/5 4 y?/3 = ¢?/3 jg y4/4 — pA/3 = p8/3, +, “, ( e Boyle’s law curves PV = constant is P? — V? = constant., the family of curves r" sin nf = a” is r” cosn = c., er the system of curves r? = a? cos 26 is r? = c’ sin 20., , series of cardioides r = a(1 — cos) is r = c(1 + cos@)., . ? [C.H. 1984, 2002], Jer toe system of curves r = csin? 6 is r? = acos@., pny the series of logarithmic spirals r = a is r = et/2(c2—8?), prArtie system of curves r” = a” cos7@ is r® = c” sin nd., Air the system of curves r” = a" sin n@ is r" = c” cos né., [C.H. 1993], Ser the system of curves x4/9 4 y4/3 = a4/3 is 27/3 — y?/3 = ¢, {C.H. 2001], 1/3 . 1/3, {Hints: qu = -2ys: Orthogonal trajectory, = = ae, Simplifying «7 !/da — y~!/%dy = 0. Int., a°/¢ — y?/ = ¢*/3], , , , 2/3, , , , , , how that the family of semi-cubical parabolas ay « gives a family, of similar and similarly situated ellipses 3y + 2x” = c?., , “Prove that the equation of the system of orthogonal trajectories of, a series of confocal and co-axial parabolas r = 2a/(1 + cos@) is, r = 2c¢/(1 — cos @)., , Show that the orthogonal trajectories of the system of co-axial circles, , h az? 4 y? + 242 +c = 0 form another system of co-axial circles, x? + y? + 2uy —c¢ = 0 when A and p are parameters and ¢ is a, given constant., , [C.H. 1985], Bron that the orthogonal trajectories of, 2 iz, , y zy, et eea7, , , , , , -d being arbitrary, is 2? + y? +c = 2a” log z., Find also when a? = 1. [C.H. 1994]

Page 3 :
414 ] An Introduction to Differential Equations, , Ki ove the differential equation of the system of confocal conics, , 2, , yo . :, PFA + Prat 1 (Vis a variable parameter), , and hence show that the system is self-orthogonal. (C.H. 1992], \\¢ (py Show that the system of co-axial parabolas y” = 4a(x + a) is, self-orthogonal. [C.H. 2000], [Hints: Diff. 2y4% = 4a, Eliminating @ and writing =p,, y = 2px +p’., For orthogonal trajectories replace p by —1/p and see that the, , resulting equation is also of the same form y = 2pr+p’y. Hence, it becomes y® = 4c(a + c) and they are self-orthogonal.], , Seow the family of confocal conics z?/A+y?/(A—A) = 1, where, A is an arbitrary constant, is self-orthogonal., , 9. Srv the family of curves cutting the family of parabolas y? =, 4az at constant angle 45°. [C.H. 1983], , Loy Fina the 45°-trajectories of the family of concentric circles, , ety =a’., , Fina the equation of the family of curves which cut the members, of the family.of hyperbolas y” + 2ry—a = c, at an angle of 45°., , [C.H. 1996], pre the orthogonal trajectories of the family of curves yore +, , 2xy — 2ax = 0 (a is a parameter). [C.H. 2004], , ind the curves that cut a system of concentric circles x2 +y=, a? at a constant angle a., , Ser Fina the equation of a set of curves, each member of which cuts, every member of the family xy =constant at the angle n/4., , (g) Determine the family of curves which intersect the lemniscate, r” = a" cos 26 at a constant angle a., , 10. Ifu+iv = f(x + iy) where u,v,z and y are all real, prove that the, , families u = constant and v = constant are orthogonal trajectories., Also prove that, , Ou Pu ay | Ov, Bat * Bt =O gaz + Hoy =O