Page 1 :
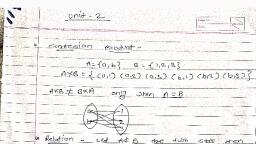
Unit 2, Introduction, In many instances we assign to each element of a set a particular element of a second set (which may be, the same as the first). For example, suppose that each student in a discrete mathematics class is assigned a, letter grade from the set {A,B,C,D, F}. And suppose that the grades are A for Adams, C for Chou, B for, Goodfriend, A for Rodriguez, and F for Stevens. This assignment of grades is illustrated in Figure 1., , DEFINITION, Let A and B be nonempty sets. A function f from A to B is an assignment of exactly one element of B to, each element of A. We write f (a) = b if b is the unique element of B assigned by the function f to the, element a of A. If f is a function from A to B, we write f : A → B., Remark: Functions are sometimes also called mappings or transformations., , DEFINITION 2 If f is a function from A to B, we say that A is the domain of f and B is the codomain of f., If f (a) = b, we say that b is the image of a and a is a preimage of b. The range, or image, of f is the set of, all images of elements of A. Also, if f is a function from A to B, we say that f maps A to B., Figure 2 represents a function f from A to B.

Page 2 :
Types Of Function-, , One to one function(Injective): A function is called one to one if for all, elements a and b in A, if f(a) = f(b),then it must be the case that a = b. It, never maps distinct elements of its domain to the same element of its codomain., , 2. Onto Function (surjective): If every element b in B has a corresponding, element a in A such that f(a) = b. It is not required that a is unique; The, function f may map one or more elements of A to the same element of B., , 3.One to one correspondence function(Bijective/Invertible): A function is, Bijective function if it is both one to one and onto function.

Page 3 :
, , , , , , , , , The range is a subset of the codomain. It is the set of all elements, which are assigned to at least one element of the domain by the, function. That is, the range is the set of all outputs., A function is injective (an injection or one-to-one) if every element, of the codomain is the output for at most one element from the, domain., A function is surjective (a surjection or onto) if every element of the, codomain is the output of at least one element of the domain., A bijection is a function which is both an injection and surjection. In, other words, if every element of the codomain is the output of exactly, one element of the domain., The image of an element xx in the domain is the element yy in the, codomain that xx is mapped to. That is, the image, of xx under ff is f(x)., , Binary Relation, Let P and Q be two non- empty sets. A binary relation R is defined to be a subset of P x Q, from a set P to Q. If (a, b) ∈ R and R ⊆ P x Q then a is related to b by R i.e., aRb. If sets P and, Q are equal, then we say R ⊆ P x P is a relation on P., , e.g, (i) Let A = {a, b, c}, B = {r, s, t}, Then R = {(a, r), (b, r), (b, t), (c, s)}, is a relation from A to B., (ii) Let A = {1, 2, 3} and B = A, R = {(1, 1), (2, 2), (3, 3)}, is a relation (equal) on A., , Domain and Range of Relation, Domain of Relation: The Domain of relation R is the set of elements in P which are, related to some elements in Q, or it is the set of all first entries of the ordered pairs in, R. It is denoted by DOM (R)., Range of Relation: The range of relation R is the set of elements in Q which are, related to some element in P, or it is the set of all second entries of the ordered pairs, in R. It is denoted by RAN (R).

Page 4 :
Let A = {1, 2, 3, 4}, B = {a, b, c, d}, R = {(1, a), (1, b), (1, c), (2, b), (2, c), (2, d)}., Solution:, DOM (R) = {1, 2}, RAN (R) = {a, b, c, d}, , Types of Relations, 1. Reflexive Relation: A relation R on set A is said to be a reflexive if (a, a) ∈ R for, every a ∈ A., Example: If A = {1, 2, 3, 4} then R = {(1, 1) (2, 2), (1, 3), (2, 4), (3, 3), (3, 4), (4, 4)}. Is a, relation reflexive?, Solution: The relation is reflexive as for every a ∈ A. (a, a) ∈ R, i.e. (1, 1), (2, 2), (3, 3),, (4, 4) ∈ R., , 2. Irreflexive Relation: A relation R on set A is said to, be irreflexive if (a, a) ∉ R for every a ∈ A., Example: Let A = {1, 2, 3} and R = {(1, 2), (2, 2), (3, 1), (1, 3)}. Is the relation R reflexive, or irreflexive?, Solution: The relation R is not reflexive as for every a ∈ A, (a, a) ∉ R, i.e., (1, 1) and (3,, 3) ∉ R. The relation R is not irreflexive as (a, a) ∉ R, for some a ∈ A, i.e., (2, 2) ∈ R., 3. Symmetric Relation: A relation R on set A is said to be symmetric iff (a, b) ∈ R ⟺, (b, a) ∈ R., Example: Let A = {1, 2, 3} and R = {(1, 1), (2, 2), (1, 2), (2, 1), (2, 3), (3, 2)}. Is a relation, R symmetric or not?, Solution: The relation is symmetric as for every (a, b) ∈ R, we have (b, a) ∈ R, i.e., (1,, 2), (2, 1), (2, 3), (3, 2) ∈ R but not reflexive because (3, 3) ∉ R., Antisymmetric Relation: A relation R on a set A is antisymmetric iff (a, b) ∈ R and (b,, a) ∈ R then a = b., Example1: Let A = {1, 2, 3} and R = {(1, 1), (2, 2)}. Is the relation R antisymmetric?

Page 5 :
Solution: The relation R is antisymmetric as a = b when (a, b) and (b, a) both belong, to R., Example2: Let A = {4, 5, 6} and R = {(4, 4), (4, 5), (5, 4), (5, 6), (4, 6)}. Is the relation R, antisymmetric?, Solution: The relation R is not antisymmetric as 4 ≠ 5 but (4, 5) and (5, 4) both, belong to R., 5. Asymmetric Relation: A relation R on a set A is called an Asymmetric Relation if, for every (a, b) ∈ R implies that (b, a) does not belong to R., , 6. Transitive Relations: A Relation R on set A is said to be, transitive iff (a, b) ∈ R and (b, c) ∈ R ⟺ (a, c) ∈ R., Example1: Let A = {1, 2, 3} and R = {(1, 2), (2, 1), (1, 1), (2, 2)}. Is the relation, transitive?, Solution: The relation R is transitive as for every (a, b) (b, c) belong to R, we have (a,, c) ∈ R i.e, (1, 2) (2, 1) ∈ R ⇒ (1, 1) ∈ R., , Equivalence Relations, A relation R on a set A is called an equivalence relation if it satisfies following three, properties:, 1. Relation R is Reflexive, i.e. aRa ∀ a∈A., 2. Relation R is Symmetric, i.e., aRb ⟹ bRa, 3. Relation R is transitive, i.e., aRb and bRc ⟹ aRc., Example:, Let A = {1, 2, 3, 4} and R = {(1, 1), (1, 3), (2, 2), (2, 4), (3, 1), (3, 3), (4, 2), (4, 4)}., Show that R is an Equivalence Relation., Reflexive: Relation R is reflexive as (1, 1), (2, 2), (3, 3) and (4, 4) ∈ R., Symmetric: Relation R is symmetric because whenever (a, b) ∈ R, (b, a) also belongs, to R., Example: (2, 4) ∈ R ⟹ (4, 2) ∈ R.

Page 6 :
Transitive: Relation R is transitive because whenever (a, b) and (b, c) belongs to R, (a,, c) also belongs to R., Example: (3, 1) ∈ R and (1, 3) ∈ R ⟹ (3, 3) ∈ R., So, as R is reflexive, symmetric and transitive, hence, R is an Equivalence Relation.