Page 1 :
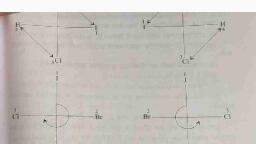
Similarly, meso-1, 2-di-sec.-butyl cyclobutane is optically, Note that the mirror image superimposes on the original, A plane of symmetry. A molecule will be said to possess, of symmetry. If a molecule possesses one or more of the above, elements of symmetrv,it is symmetrical; on the other hand, if it, symmetry, (ii) a centre of symmetry and (iii an alternating axis, phic forms if it is devoid of the etements of sRminetry (however,, tiomorphic formş. Further, a compound can exist in enantiomor-, for internal rotation about single bond), i.e., it must exist in enan-, molecule to show optical activity is that the geometrical structure, of the molecule should not superimpose on its mirror image (allowing, Conditions for Optical Activity (Asymmetric Molecule):, The only necessary inflexible and sufficient condition for a, modification has some physical properties different from those of, produce optically inactive, (±) or racemic (r) lactic acid. Racemic, (+)-lactic acid and (-)-lactic acid are mixed together, it will, pound called racemic, dl or (±)-form. Thus if equal amounts of, quantities, it results in the formation of an optically inactive com-, (iii) When the two enantiomers are mixed in equimolecular, 154, 155, quantities, it results in the formation of an, as a whole is symmetrical and hence its mirror, Stereochemistry, Stereochemistry, optically inactive com-, cause the molecule, OH, the two enantiomers (see example of dl-tartaric acid)., 6-4c. Conditions for Optical Activity (Asymmetric Molecule):, --Coom, -C, for internal rotation about single bond), i.e., it must exist in eng, HOC, COOH,, ÕH, phic forms if it is devoid of the eltements of syimmetry (hower, see allenes, spiro and diphenyl compounds), viz. (i) a plane, symmetry, (ii) a centre of symmetry and (iii) an alternating a, of symmetry. If a molecule possesses one or more of the abo, elements of symmetrv, it is symmetrical; on the other hand e, does not possess either of these elements of symmetry, it is asym, metric. Now let us deal all these elements of symmetry in detail, i A plane of symmetry. A molecule will be said to possess, a plane of syminetry if it can be divided into two_equal halves in onu, plane and tlus the atoms or groups on one side of the plane form, mirror image of those on the other side. For example, a compound, Cabd. Cabd, having the plane diagram' formula I (meso-form), possesses a plane of symmctry, whereas the other two jsomers, II and HI, do-not possess any plane of symmetry ; and hence, compound I is optically inactive (symmetrical); whereas the com, pounds II and III are optically active_(provided they also lack a, centre of symmetry and an alternating axis of symmetry; and, actually they do so)., b., Two superimposable forms of the meso-'artaric acid., S), Citz, be Celye, COHS, the moled, Plane of symmetry, meso-1, 2-di-sec-butyl cyclobutane, 19, an imaginary point in the centre of a molecule from which if lines, ure drawn, on any group, on both the sides to an equal distance, it, "lvides the molecule into two equal halves which are the mirror, avt of each other. For example, 2, 4-dimethylclobutane-1,, 3-dicarboxylic acid possesses a centre of symmetry which is the, A centre (point) of symmetry. A centre of symmetry is, b., a d, centre of the ring., CO, a--d, d-, CH3, a, --plane of symmetry, d--a 1, a--d, 2, a- d., 9., b., meso form, 1, II, III, The three forms of tartaric acid, CH(OH)CCOH.CH(OH}CECH, (discussed later) completely coincide with theset hree forms of the, compound Cabil. Cabd. Phus meso- tartaric acid, although_con-, tains two asymmetric carbon atoms, it is optically inactive be-, CH3, 1. A plane of symmetry may be demonstrated successfully with the help, of both tetrahedral (three dimensional) and plane (two dimensional) formulae., REDMI NOTE 8 PRO, 88, Co AI QUAD CAMERA