Page 1 :
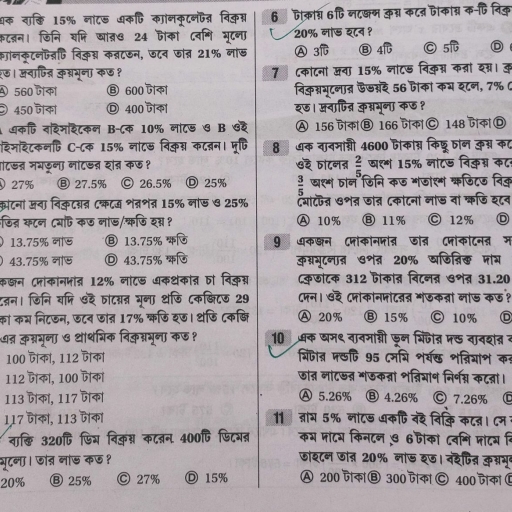
qos re “, , 20 RUDIMENTS OF PHYSICS, , ing with an acceleration, : stand moving, 6. The distance 8 from, res, , € travelled by a particle startin, 4/3 m, , s-?, in the third second is,, , “ [PMT, 08, voy, (b) Pin (c)6m (d) 4m : ], , ay 5, ( i es given below represents, * A body stans moving with an initial velocity. Which of the ihc rereading velco, the variation of velocity with time when the body is moving with.an J ;, oO, , , , , , , , , , ‘@ © (d), TP t Pg. Ee f “ T, ts Cagle yee to . Pub, = 8A particle moves with aaapitial velocity u ait an acceleration f = at. Which of the, ~~ following relations is valid? ~~ 53 ne be wa Oe — . =, (jveu O)vautar. Qs u+ Jat () w= 4 at, 9., , A body travels 200 cm in the first two seconds and 220 cm. in the next four seconds., The velocity of the body at the end of 7th second from the start will be (LLT., 764], , (a) Sem s-!—(b) 10.5 em 57! (orem st (d) 11.Scm gal fe 8, , 10. The ‘time-displacement graph for a, uniform acceleration is given by, , Particle moving with non-uniform velocity but a, , , , , , (a) TI. (b) 7 cae @ Tt, = 2 < 2 |, € g § a, 2 5 5 Z |, 9 ° oO oO, 3 3 ; 8 g, S 2 & e, Z = 3 ~ zu 3, * time() > time (1) =>, , time (1) >, , 11, The time variation of position is shown in the figure given below;, , time (t) >, , (LLT; 79], , In this case, the correct conclusion is, jt can never be observed in nature , (b) it can always happen ih nature, , time () 3, , , , (c) it can occur occasionally in nature, Cc, , , , (d) none of the conclusions is correct,, , P's position) R

Page 2 :
12. A car accelerates from rest.at a const, at a constant rate’ to come to rest. |, , velocity reached by the car is, , +, a a+ ZB, , 13. A particle starts-from the origin, line. At time ¢ = h,, of the motion of th, , (a), , , , 1221, , , , @) (37) (b) (4): () (, , (b), , a, at Bp, , , , CHAPTER THREE O KINEMATICS 7], , ant rate @ for sometime after which it decelerates, f the total time lapsed is ‘rf’ seconds, the maximum, , ee, , (Model question of WBB of JEE; LLT’ 78] , , , , , at time 1 = 0 with'a uniform velocity v in a straight, the velocity suddenly changes to - v. The distance-time (s ~ 1) graph, particle upto to the time ¢ = 2 1, is represented by, , 14, A ball is: projected vertically upwards. Which one of the following graphs ‘represents, the velocity of the ball during its flight when. the air resistance is‘ignored 2°:, , , , mr -19, , (c), , ©) @),, z i 7 i, t Ke ea, wii, , 15. Which of the following ‘position = time graph is not-realistic in natu, , x, , |, , a ie _@), , re?, , , , , , , , , , , , i—, , 1, , —, , sem, , inci

Page 3 :
22 RUDIMENTS OF PHYSICS, , i height h, . 1 a velocity Vp ata at, 16. A ball is relensed from a balloon moving upward with, , time 1 = 0. The speed-time graph is, , (d), (a) (b) ft, It, , locity-time sigh for, , , , ts, 17. Which one of the graphs in the seine is pion meee the ve, 4 the ball ?, , 18. A body starts moving with ani initial velocity and a uniform acceleration. The variation, of velocity(v) with time(s) is represented by the. graph., , ) (b) © @, v v ¥ ¥,, 1 1 1 i, I> I> 19 >., , 19. A small block descends without friction along an inclined plane from rest at time t = 0., If the distances traversed during the time t= 1s to t = 2s be x and from t = 4s to t = 5s, be x’, thén the ratio. x’ : x will be, , (a) 1 (o+)2 (c)3.- (d)4 : [LLT., 2004], 20. The velocity-time graph of an ascending lift is given below. , [v is in m/s & fis in seconds], , , , , , 0 : tro 15 ee . ‘ ;, The maximum height ascended by the lift is, (a) 60m ~ (b) 50m = (c) 4m (d) 30m, , 21. Which one of the Bi) graphs represents the motion of a particle i in one dimension ?, , AWRY

Page 4 :
CHAPTER THREE O KINEMATICS 73, , 22. Acceleration (f) — time (r), , 25. A particle starting from rest moves along a straight line with a uniform acceleration., , 26. The distances traversed by a body in the Sth and ¢l, , 27. If the velocity 4 of a movi, , graph of a particle is s i [rene], , the adjoining figure, are : |, et, , |, , Milt, , —, , , , Which ont oF the fe i, following Tepresents the appropriate velocity (v) - time () graph ?, , (a), t e),. V\ ©), @,, , Ac |, ‘ar runs at a constant speed on a circular track of radius 100m, taking 62.85 for every, , circula i i, = r lop: The average velocity and average speed for each circular loop respectively, , , , 17, , (a) 10ms-!, 10ms-!(b) 10ms!, 0 (©) 0,0 (4) 0, 10ms"!,, , A particle Moves along a straight line OX. At a time:#(in second) the distance x(in metre), of the particle from O is given by x = 40 + 121 - 13, How long would the particle travel |, before coming to rest é, , ‘(a) 56m_—(b) 16m, (c) 24m — (4) 40m. : [PMT, 2006], , The nature of the graph showing the distance(s) traversed by the body with respect to, time(t) is given by [J.E.E., 89], , (a) (b) (c) — (d), s|- / s : : 4, : : t tT T :, : ; pm : i 19 tm, , 1 he 7Fth second of its journey are 25, cm and 33 cm ‘respectively. The velocity of the body at the end of the 9th second from |, the statis . eee ‘, , (a) 40 ‘cm/s . (b) 42 cm/s (c) 43.5 cm/s wey cm/s {H.S., 1995], ing particle. at any distance x satisfies the equation, y2 = 4(x sin x + cosx), then the acceleration is, , (a) 2x cosx (b) 2(x cosx - sinx) (c) 2x sinx (d) 2(x cosx + sinx), , , , r=, , , , 2

Page 5 :
74 RUDIMENTS OF PHYSICS, uniform acceleration. Which, , night tine with a rompect 2 velocity (v) 2, , 28. A body starts moving from rest along @ strat rent(s) with, of the graphs will represent the change of displacen, , d), @) ) © °,, y 3 5 om, 4 io |, 33 s3 ‘i og oe, , 29. In 1.0 sec. a particle goes from point A to point a, , B moving in a semi-circle of radius 1.0.m as, shown in ‘the figure. The magnitude of the, average velocity is :, , (a) 3.14ms-!—(b) 2.0 ms“!, (c) 1.0 ms“! (d) zero. B UIT, 799], 30. A particle starting from the origin (0, 0)-moves in a straight line in the (x, y) plane. Its, , co-ordinates at a later time are (/3, 3). The path of the particle makes with the x-axis, an angle of : ~, , (a) 30° (b) 45° () 60° (d) 0° (AIEEE, °07], , 31. A body starts moving with an initial velocity. If it moves with a gradually decreasing ., acceleration, the time(t) — velocity(u) graph is represented by a, , @ (b) © @® yp., v v " v ¥, T + tT : at, _ t- t~ tim rs ‘, , 32. A body is at rest at x = 0. At? = 0, it starts moving in the positiv, constant acceleration. At the same instant another body passesth ens, -the positive x — direction with a constant speed. The pogj rough x, x, (0) after time ‘1’, , direction with, , ~ *)) as a function of time ‘? 7, , ‘i (x, -x,), aya Oe ) | &1—x), : (c) | 1-2, @)4-x)°