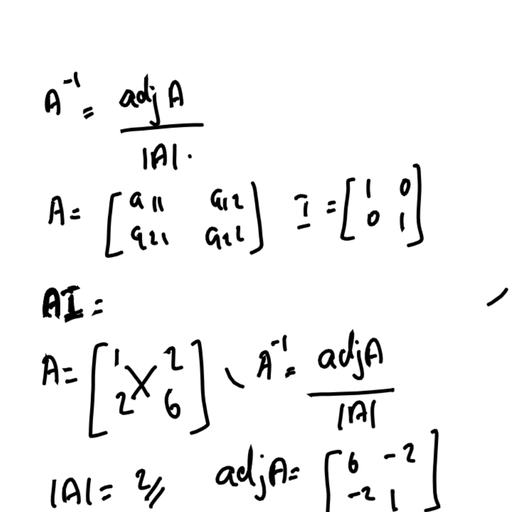Page 1 :
984, , Chapter 12 Vector-Valued Functions, , 12.1, , Vector-Valued Functions and Space Curves, In Section 10.2 we saw that the position of an object such as a boat or a car moving, in the xy-plane can be described by a pair of parametric equations, x � f(t), , y � t(t), , where f and t are continuous functions on a parameter interval I., Using vector notation, we can denote the position of the object in an equivalent, and somewhat abbreviated form via its position vector r as follows: For each t in, I, the position vector r of the object is the vector with initial point at the origin and, terminal point ( f(t), t(t)). In other words,, r(t) � 具 f(t), t(t)典 � f(t)i � t(t)j, , t僆I, , As t takes on increasing values, the terminal point of r(t) traces the path of the object, which is a plane curve C. This is illustrated in Figure 1 for the parameter interval, I � [a, b]., y, C, , ( f(a), g(a)), , ( f(t), g(t)), ( f(b), g(b)), , FIGURE 1, As t increases from a to b, the terminal, point of r traces the curve C., , [, a, , t, , ], b, , r(a), , t, , r(t), , r(b), x, , 0, , Parameter interval [a, b], , Similarly, in 3-space we can describe the position of an object such as a plane or, a satellite using the parametric equations, x � f(t), , y � t(t), , z � h(t), , where f, t, and h are continuous functions on a parameter interval I. Equivalently, we, can describe its position using the position vector r defined by, r(t) � 具 f(t), t(t), h(t)典 � f(t)i � t(t)j � h(t)k, , t僆I, , As t takes on increasing values, the terminal point of r(t) traces the path of the object,, which is a space curve C. (See Figure 2.), z, ( f(t), g(t), h(t)), C, ( f(a), g(a), h(a)), , FIGURE 2, As t increases from a to b, the terminal, point of r traces the curve C., , [, a, , t, , ], b, , r(t), , r(a), t, , 0, , ( f(b), g(b), h(b)), r(b), y, , Parameter interval [a, b], x, , The function r is called a vector-valued function, or vector function, of a real, variable t because its value r(t) is a vector and its domain (parameter interval) is a, subset of the real numbers.
Page 2 :
12.1, , Vector-Valued Functions and Space Curves, , 985, , DEFINITION Vector Function, A vector-valued function, or vector function, is a function r defined by, r(t) � f(t)i � t(t)j � h(t)k, where the component functions f, t, and h of r are real-valued functions of the, parameter t lying in a parameter interval I., , Unless otherwise specified, the parameter interval will be taken to be the intersection of the domains of the real-valued functions f, t, and h., , EXAMPLE 1 Find the domain (parameter interval) of the vector function, 1, r(t) � h , 1t � 1, ln ti, t, Solution The component functions of r are f(t) � 1>t, t(t) � 1t � 1, and, h(t) � ln t. Observe that f is defined for all values of t except t � 0, t is defined for, all t � 1, and h is defined for all t � 0. Therefore, f, t, and h are all defined if t � 1,, and we conclude that the domain of r is [1, ⬁)., , Curves Defined by Vector Functions, As was mentioned earlier, a plane or space curve is the curve traced out by the terminal point of r(t) of a vector function r as t takes on all values in a parameter interval., , EXAMPLE 2 Sketch the curve defined by the vector function, r(t) � 具3 cos t, �2 sin t典, Solution, , 0 � t � 2p, , The parametric equations for the curve are, x � 3 cos t, , and, , y � �2 sin t, , Solving the first equation for cos t and the second equation for sin t and using the identity cos2 t � sin2 t � 1, we obtain the rectangular equation, y2, x2, �, �1, 9, 4, The curve described by this equation is the ellipse shown in Figure 3. As t increases, from 0 to 2p, the terminal point of r traces the ellipse in a clockwise direction., y, 2, , (t � 3π2 ), (3 cos t, �2 sin t), , FIGURE 3, As t increases from 0 to 2p, the, terminal point of the vector r(t) traces, y2, x2, the ellipse, �, � 1 in a clockwise, 9, 4, direction, starting and ending at (3, 0)., , (t � π), �3, [, 0, , ], 2π, , r(t), 0, , t, , Parameter interval [0, 2π], , �2, , (t � 0, 2π), x, , 3, , (t � π2 )
Page 3 :
986, , Chapter 12 Vector-Valued Functions, , EXAMPLE 3 Sketch the curve defined by the vector function, r(t) � (2 � 4t)i � (�1 � 3t)j � (3 � 2t)k, Solution, , 0�t�1, , The parametric equations for the curve are, x � 2 � 4t, , y � �1 � 3t, , z � 3 � 2t, , which are parametric equations of the line passing through the point (2, �1, 3) with, direction numbers �4, 3, and 2. Because the parameter interval is the closed interval, [0, 1], we see that the curve is a straight line segment: Its initial point (2, �1, 3) is the, terminal point of the vector r(0) � 2i � j � 3k, and its terminal point (�2, 2, 5) is, the terminal point of the vector r(1) � �2i � 2j � 5k. (See Figure 4.), z, , (�2, 2, 5), C, , 5, , r(1), (2, �1, 3), , r(t), r(0), , FIGURE 4, As t increases from 0 to 1, the tip of, r(t) traces the straight line segment, from (2, �1, 3) to (�2, 2, 5)., , z, , [, 0, , ], 1, , 1 1, 2, , t, , Parameter interval [0, 1], , 2, , 3, , 3, , y, , x, , EXAMPLE 4 Sketch the curve defined by the vector function, r(t) � 3i � tj � (4 � t 2)k, , 4, , Solution, , r(t), , �2 � t � 2, , The parametric equations for the curve are, x�3, , y�t, , z � 4 � t2, , Eliminating t from the second and third equations, we obtain, 2, (3, �2, 0), x, , 3, , (3, 2, 0), , FIGURE 5, As t increases from �2 to 2, the terminal point of r(t) traces the part of the, parabola lying in the plane x � 3 from, the point (3, �2, 0) to the point, (3, 2, 0)., , z � 4 � y2, , y, , Since the x-coordinate of any point on the curve must always be 3, as implied by the, equation x � 3, we conclude that the desired curve is contained in the parabola, z � 4 � y 2, which lies in the plane x � 3. In fact, as t runs from �2 to 2, the terminal point of r traces the part of the parabola starting at the point (3, �2, 0) [since, r(�2) � 3i � 2j] and ending at the point (3, 2, 0) [since r(2) � 3i � 2j], as shown, in Figure 5., , EXAMPLE 5 Sketch the curve defined by the vector function, r(t) � 2 cos ti � 2 sin tj � tk, Solution, , 0 � t � 2p, , The parametric equations for the curve are, x � 2 cos t, , y � 2 sin t, , z�t
Page 4 :
12.1, z, , From the first two equations we obtain, y 2, x 2, a b � a b � cos2 t � sin2 t � 1, 2, 2, , (2, 0, 2π), (t � 2π), , r(t), , x, , 987, , Vector-Valued Functions and Space Curves, , (0, 2, π_2 ), y, , (2, 0, 0), (t � 0), , FIGURE 6, As t increases from 0 to 2p, the, terminal point of r(t) traces the, helix beginning at (2, 0, 0) and, terminating at (2, 0, 2p) ., , x 2 � y2 � 4, , or, , This says that the curve lies on the right circular cylinder of radius 2, whose axis is, the z-axis. At t � 0, r(0) � 2i, and this gives (2, 0, 0) as the starting point of the curve., Since z � t, the z-coordinate of the point on the curve increases (linearly) as t increases,, and the curve spirals upward around the cylinder in a counterclockwise direction,, terminating at the point (2, 0, 2p) [r(2p) � 2i � 2pk]. The curve, called a helix, is, shown in Figure 6., , EXAMPLE 6 Find a vector function that describes the curve of intersection of the, cylinder x 2 � y 2 � 4 and the plane x � y � 2z � 4. (See Figure 7.), z, , z, , 4, , 4, x2 � y2 � 4, C, , x � y � 2z � 4, , 4, , 4, , y, , x, , FIGURE 7, , 4, , 4, , y, , x, , (a) Intersection of the plane and the cylinder, , (b) Curve of intersection, , Solution If P(x, y, z) is any point on the curve of intersection C, then the x- and, y-coordinates lie on the right circular cylinder of radius 2 and axis lying along the, z-axis. Therefore,, x � 2 cos t, , and, , y � 2 sin t, , To find the z-coordinate of the point, we substitute these values of x and y into the, equation of the plane, obtaining, 2 cos t � 2 sin t � 2z � 4, , or, , z � 2 � cos t � sin t, , So a required vector function is, r(t) � 2 cos ti � 2 sin tj � (2 � cos t � sin t)k, , 0 � t � 2p, , You might have noticed that the space curves in Examples 4, 5, and 6 are relatively, easy to sketch by hand. This is partly because they are relatively simple and partly, because they lie in a plane. For more complicated curves we turn to computers., , EXAMPLE 7 Use a computer to plot the curve represented by, r(t) � (0.2 sin 20t � 0.8) cos ti � (0.2 sin 20t � 0.8) sin tj � 0.2 cos 20tk, 0 � t � 2p
Page 5 :
988, , Chapter 12 Vector-Valued Functions, , Solution, , The curve is shown in Figure 8., 1.0, 0.5, 0.0, , z, , �0.5, �1.0, 0.2, 0.0, , x, , �0.2, �1.0, , FIGURE 8, The curve in Example 7 is, called a toroidal spiral, because it lies on a torus., , �0.5, , 0.0, y, , 0.5, , 1.0, , Limits and Continuity, Because the range of the vector function r is a subset of vectors in two- or threedimensional space, the properties of vectors given in Chapter 11 can be used to study, the properties of vector functions. For example, we add two vector functions componentwise. Thus, if, r1(t) � f1(t)i � t1(t)j � h 1(t)k, , and, , r2(t) � f2 (t)i � t2(t)j � h 2(t)k, , then, (r1 � r2)(t) � r1(t) � r2(t) � [ f1 (t) � f2 (t)]i � [t1(t) � t2(t)]j � [h 1(t) � h 2 (t)]k, Similarly, if c is a scalar, then the scalar multiple of r by c is, (cr)(t) � cr(t) � cf(t)i � ct(t)j � ch(t)k, Next, because the components f, t, and h of the vector function r are real-valued, functions, we can investigate the notions of limits and continuity involving r using the, properties of such functions. As you might expect, the limit of r(t) is defined in terms, of the limits of its component functions., , DEFINITION The Limit of a Vector Function, Let r be a function defined by r(t) � f(t)i � t(t)j � h(t)k. Then, lim r(t) � C lim f(t)D i � C lim t(t)D j � C lim h(t)D k, t→a, , t→a, , t→a, , t→a, , provided that the limits of the component functions exist., , To obtain a geometric interpretation of lim t→a r(t) , suppose that the limit exists., Let lim t→a f(t) � L 1, lim t→a t(t) � L 2, and lim t→a h(t) � L 3, and let L � L 1i � L 2 j �, L 3k. Then, by definition, lim t→a r(t) � L. This says that as t approaches a, the vector, r(t) approaches the constant vector L. (See Figure 9.)
Page 6 :
12.1, , Vector-Valued Functions and Space Curves, , 989, , z, , Historical Biography, Hulton Archive/Getty Images, , r(t), 0, [, t, , ], a, , t, , y, , Parameter interval, , JOSIAH WILLARD GIBBS, (1839–1903), Josiah Willard Gibbs, an American mathematician and physicist, did not attain the, level of fame that his European contemporaries enjoyed until his work was translated into German in 1891. He made many, contributions to the study of vector analysis, thermodynamics, and electromagnetics, and provided a firm mathematical foundation for statistical mechanics. Because of, the depth and application of his work,, Albert Einstein referred to Gibbs as “the, greatest mind in American history.” Gibbs’s, mother was an amateur ornithologist, and, his father was a professor of sacred literature at Yale. Gibbs, who began school at, the age of 9, eventually attended Yale himself. He earned a bachelor’s degree at the, age of 19 and showed promise that he, would follow his father into the area of, philology. At the time, the American academy awarded doctorates in only applied, science and mathematics, yet Gibbs’s doctoral thesis was written on spur gear, design. As a result of this thesis, he was, awarded the first doctorate of engineering, in the United States. In 1866 he embarked, on a three-year trip abroad, where he, attended lectures in physics at many European universities. Upon his return to the, United States, Gibbs was appointed to a, position of professor of mathematical, physics at Yale. He presented his first work, of vector analysis while teaching there., Gibbs’s courses included the first collegelevel vector analysis course. Using Gibbs’s, class notes, Edwin Wilson wrote a textbook,, published in 1901, that was titled Gibbs’, Vector Analysis. This textbook reached a, wider audience than Gibbs’s own publications did, and it led to Gibbs receiving, many awards, including honorary doctor of, science degrees from Erlangen, Williams, College, and Princeton University., , L, , x, , FIGURE 9, lim t→a r(t) � L means that as t approaches a, r(t) approaches L., , EXAMPLE 8 Find lim t→0 r(t), where r(t) � 1t � 2i � t cos 2tj � e�t k., Solution, , lim r(t) � C lim 1t � 2 D i � C lim t cos 2tD j � C lim e�tD k, t→0, , t→0, , t→0, , t→0, , � 12i � k, The notion of continuity is extended to vector functions via the following definition., , DEFINITION Continuity of a Vector Function, A vector function r is continuous at a if, lim r(t) � r(a), t→a, , A vector function r is continuous on an interval I if it is continuous at every, number in I., , It follows from this definition that a vector function is continuous at a if and only, if each of its component functions is continuous at a., , EXAMPLE 9 Find the interval(s) on which the vector function r defined by, r(t) � 1ti � a, , 1, t �1, 2, , bj � ln tk, , is continuous., Solution The component functions of r are f(t) � 1t, t(t) � 1>(t 2 � 1), and, h(t) � ln t. Observe that f is continuous for t � 0, t is continuous for all values of t, except t � �1, and h is continuous for t � 0. Therefore, r is continuous on the intervals (0, 1) and (1, ⬁).
Page 7 :
990, , Chapter 12 Vector-Valued Functions, , 12.1, , CONCEPT QUESTIONS, 3. a. What does it mean for a vector function r(t) to be continuous at a? Continuous on an interval I ?, b. Give an example of a function r(t) that is defined on the, interval (�1, 1) but fails to be continuous at 0., , 1. a. What is a vector-valued function?, b. Give an example of a vector function. What is the, parameter interval of the function that you picked?, 2. Let r(t) be a vector function defined by, r(t) � 具 f(t), t(t), h(t)典., a. Define lim t→a r(t)., b. Give an example of a vector function r(t) such that, lim t→1 r(t) does not exist., , 12.1, , EXERCISES, , In Exercises 1–6, find the domain of the vector function., 1. r(t) � ti �, , (c), , 1, j, t, , (d), z, , z, , 2. r(t) � cos ti � 2 sin tj � 1t � 1 k, 3. r(t) � h 1t,, , 4. r(t) � h, , 1, , ln ti, t�1, , 1, , e�t i, 1t � 1, , 5. r(t) � ln ti � cosh tj � tanh tk, 3, 6. r(t) � 1t i � e1>tj �, , 0, y, , 1, k, t�2, , 0, x, , y, x, (e), , In Exercises 7–12, match the vector functions with the curves, labeled (a)–(f). Explain your choices., , (f ), z, , 7. r(t) � t 2 i � t 2j � t 2 k, , z, , 8. r(t) � 2 cos 2ti � tj � 2 sin 2tk, 9. r(t) � ti � tj � a, , 1, t �1, 2, , bk, , 10. r(t) � t sin ti � t cos tj � tk, 0 � t � 10p, 11. r(t) � 2 cos ti � 3 sin tj � e0.1t k,, , 0, , t�0, , 0, , 12. r(t) � cos ti � sin tj � sin 3tk, (b), , (a), z, , y, , x, , y, x, z, , In Exercises 13–26, sketch the curve with the given vector function, and indicate the orientation of the curve., 13. r(t) � 2ti � (3t � 1)j,, , �1 � t � 2, , 14. r(t) � 1t i � (4 � t)j,, , t�0, , 15. r(t) � 具t , t 典,, 2, , 3, , �1 � t � 2, , 16. r(t) � 2 sin ti � 3 cos tj,, 17. r(t) � e i � e j,, t, , 0, y, , 0, y, x, x, , 2t, , �⬁, , 0 � t � 2p, t, , ⬁, , 18. r(t) � 具1 � 2 cos t, 3 � 2 sin t典,, , 0 � t � 2p, , 19. r(t) � (1 � t)i � (2 � t)j � (3 � 2t)k,, , �⬁, , t, , 20. r(t) � (2 � t)i � (3 � 2t)j � (2 � 4t)k, 0 � t � 1, 21. r(t) � 具t, t 2, t 3典,, , V Videos for selected exercises are available online at www.academic.cengage.com/login., , t�0, , ⬁
Page 8 :
12.1, 22. r(t) � 2 cos ti � 4 sin tj � 3k,, , 0 � t � 2p, , 23. r(t) � 2 cos ti � 4 sin tj � tk,, , 0 � t � 2p, , 24. r(t) � ti � 2tj � sin 2tk,, , �⬁, , 25. r(t) � 具t cos t, t sin t, t典, �⬁, , 42. lim c a, , ⬁, , t, , t→�⬁, , Hint: Show that it lies on a cone., , 26. r(t) � et cos ti � et sin tj � et k,, , �⬁, , t, , ⬁, , cas In Exercises 27–30 use a computer to graph the curve described, , by the function., , t�1, bi � e2t j � tan�1 tkd, 2t � 1, , In Exercises 43–48 find the interval(s) on which the vector function is continuous., 43. r(t) � 1t � 1 i �, , 1, j, t, , 27. r(t) � 2 sin pti � 3 cos ptj � 0.1tk, 0 � t � 10, , 44. r(t) � sin ti � cos tj � tan�1 tk, , 28. r(t) � (t 2 � t � 1)i � (t 2 � 1)j � t 3k,, , 45. r(t) � h, , cos t � 1, 1t, ,, , te�1>t i, t, 1 � 2t, , 46. r(t) � a, , t2 � 4, , 29. r(t) � sin 3t cos ti � sin 3t sin tj �, , �3 � t � 3, , t, k,, 2p, , �2p � t � 2p, , (rotating sine wave), 1, 1, t2, sin ti � cos tj �, k,, 2, 2, 100p2, (Fresnel integral spiral), , 30. r(t) �, , 991, , 1 2t 2, 41. lim h e�t, , 2, i, t→⬁, t t �1, , ⬁, , t, , Vector-Valued Functions and Space Curves, , 0 � t � 10p, , 31. a. Show that the curve, , � 21 � 0.09 cos2 10t sin tj � 0.3 cos 10tk, lies on a sphere., b. Graph the curve described by r(t) for 0 � t � 2p., 32. a. Show that the curve, r(t) � (1 � cos 12t) cos ti � (1 � cos 12t) sin tj, � (1 � cos 12t)k, lies on a cone., b. Graph the curve described by r(t) for 0 � t � 2p., In Exercises 33–36, find a vector function describing the curve, of intersection of the two surfaces., 33. The cylinder x 2 � y 2 � 1 and the plane x � y � 2z � 1, , 3, bi � sin�1 tj � 1, tk, , 47. r(t) � e�t i � cos 14 � t j �, 48. r(t) �, , r(t) � 21 � 0.09 cos2 10t cos ti, , 2t, , 1, t2 � 1, , k, , 1, i � tan tj � e�t cos tk, 1t, , 49. Trajectory of a Plane An airplane is circling an airport in a, holding pattern. Suppose that the airport is located at the, origin of a three-dimensional coordinate system and that, the trajectory of the plane traveling at a constant speed is, described by, r(t) � 44,000 cos 60ti � 44,000 sin 60tj � 10,000k, where the distance is measured in feet and the time is, measured in hours. What is the distance covered by the, plane over a 2-min period?, 50. Temperature at a Point Suppose that the temperature at a, point (x, y, z) in 3-space is T(x, y, z) � x 2 � 2y 2 � 3z 2, and that the position of a particle at time t is described, by r(t) � 具t, t 2, et典. What is the temperature at the point, occupied by the particle when t � 1?, , 35. The cone z � 2x 2 � y 2 and the plane x � y � z � 1, , In Exercises 51–54, suppose that u and v are vector functions, such that lim t→a u(t) and lim t→a v(t) exist and c is a constant., Prove the given property., , 36. The paraboloid z � x 2 � y 2 and the sphere x 2 � y 2 � z 2 � 1, , 51. lim [u(t) � v(t)] � lim u(t) � lim v(t), , In Exercises 37–42, find the given limit., , 52. lim cu(t) � c lim u(t), , 34. The cylinder x 2 � y 2 � 4 and the surface z � xy, , 37. lim [(t � 1)i � cos tj � 3k], 2, , t→0, , 39. lim c 1t i � a, , t2 � 4, t, bkd, bj � a 2, t�2, t �1, , 40. lim� ccos ti �, , tan t, j � t ln tkd, t, , t→0, , t→a, , t→a, , t→a, , t→a, , 53. lim [u(t) ⴢ v(t)] � lim u(t) ⴢ lim v(t), t→a, , sin t, , cos ti, 38. lim he�t,, t→0, t, t→2, , t→a, , 54. lim [u(t), t→a, , t→a, , v(t)] � lim u(t), t→a, , t→a, , lim v(t), , t→a, , 55. a. Prove that if r is a vector function that is continuous at, a, then 冟 r 冟 is also continuous at a., b. Show that the converse is false by exhibiting a vector, function r such that 冟 r 冟 is continuous at a but r is not, continuous at a.
Page 9 :
992, , Chapter 12 Vector-Valued Functions, In Exercises 59–62, determine whether the statement is true or, false. If it is true, explain why. If it is false, explain why or give, an example to show that it is false., , 56. Evaluate, lim h, , h→0, , (t � h) � t cos(t � h) � cos t e, ,, ,, h, h, 2, , 2, , �e, i, h, , t�h, , t, , 59. The curve defined by r1(t) � t 2 i � t 2j � t 2 k is the same as, the curve defined by r2(u) � ui � uj � uk., , 57. Evaluate, lim c, t→0, , 60. If f, t, and h are linear functions of t for t in (�⬁, ⬁), then, r(t) � f(t)i � t(t)j � h(t)k defines a line in 3-space., , ln(1 � t 2), 1 � cos t, sin t, i�, j�, kd, 2, t, t, cos t � e�t, , 61. The curve defined by r(t) � f(t)i � t(t)j � ck, where c is a, constant, is a curve lying in the plane z � c., , 58. a. Find a vector function describing the curve of intersection of the plane x � y � 2z � 2 and the paraboloid, z � x 2 � y 2., b. Find the point(s) on the curve of part (a) that are closest, to and farthest from the origin., , 12.2, , 62. If r is continuous on an interval I and if a is any number in, I, then lim t→a r(t) � r(a)., , Differentiation and Integration of Vector-Valued Functions, The Derivative of a Vector Function, The derivative of a vector function is defined in much the same way as the derivative, of a real-valued function of a real variable., , DEFINITION Derivative of a Vector Function, The derivative of a vector function r is the vector function r¿ defined by, r¿(t) �, , r(t � h) � r(t), dr, � lim, dt, h→0, h, , provided that the limit exists., , To obtain a geometric interpretation of this derivative, let r be a vector function,, and let C be the curve traced by the tip of r. Let t be a fixed but otherwise arbitrary, number in the parameter interval I. If h � 0, then the vector r(t � h) � r(t) lies on, the secant line passing through the points P and Q, the terminal points of the vectors, r(t) and r(t � h), respectively. (See Figure 1.), z, , z, r (t), , r(t � h) � r(t), , P, r(t), , P, Q, , Q, , r(t � h) � r(t), h, , r(t � h), t, , t�h, , Parameter interval, , 0, , t, x, (a), , C, y, , 0, x, , C, y, , (b), , FIGURE 1, r(t � h) � r(t), As h approaches 0, Q approaches P along C, and the vector, approaches the tangent vector r¿(t)., h
Page 10 :
12.2, , Differentiation and Integration of Vector-Valued Functions, , 993, , The vector [r(t � h) � r(t)]>h, which is a scalar multiple of r(t � h) � r(t), also, lies on the secant line. (See Figure 1b.) As h approaches 0, the number t � h approaches, t along the parameter interval, and the point Q, in turn, approaches the point P along, the curve C. As a consequence, the vector [r(t � h) � r(t)]>h approaches the fixed, vector r¿(t), which lies on the tangent line to the curve at P. In other words, the derivative r¿ of the vector r may be interpreted as the tangent vector to the curve defined, by r at the point P, provided that r¿(t) 0. If we divide r¿(t) by its length, we obtain, the unit tangent vector, T(t) �, , r¿(t), 冟 r¿(t) 冟, , which has unit length and the direction of r¿., The following theorem tells us that the derivative r¿ of a vector function can be, found by differentiating the components of r., , THEOREM 1 Differentiation of Vector Functions, Let r(t) � f(t)i � t(t)j � h(t)k, where f, t, and h are differentiable functions of, t. Then, r¿(t) � f ¿(t)i � t¿(t)j � h¿(t)k, , PROOF We compute, r(t � ⌬t) � r(t), ⌬t→0, ⌬t, , We use ⌬t instead of h so as not to confuse the increment, of t with the component function h., , r¿(t) � lim, , � lim c, , f(t � ⌬t)i � t(t � ⌬t)j � h(t � ⌬t)k � [f(t)i � t(t)j � h(t)k], , � lim c, , t(t � ⌬t) � t(t), f(t � ⌬t) � f(t), h(t � ⌬t) � h(t), i�, j�, kd, ⌬t, ⌬t, ⌬t, , ⌬t, , ⌬t→0, , ⌬t→0, , d, , t(t � ⌬t) � t(t), f(t � ⌬t) � f(t), h(t � ⌬t) � h(t), di � c lim, d j � c lim, dk, ⌬t→0, ⌬t, ⌬t→0, ⌬t, ⌬t→0, ⌬t, , � c lim, , � f ¿(t)i � t¿(t)j � h¿(t)k, , EXAMPLE 1, a. Find the derivative of r(t) � (t 2 � 1)i � e�t j � sin 2tk., b. Find the point of tangency and the unit tangent vector at the point on the curve, corresponding to t � 0., Solution, a. Using Theorem 1, we obtain, r¿(t) � 2ti � e�t j � 2 cos 2tk, b. Since r(0) � i � j, we see that the point of tangency is (1, 1, 0). Next, since, r¿(0) � �j � 2k, we find the unit tangent vector at (1, 1, 0) to be, T(0) �, , r¿(0), �j � 2k, 1, 2, �, ��, j�, k, 冟 r¿(0) 冟, 11 � 4, 15, 15
Page 11 :
994, , Chapter 12 Vector-Valued Functions, , y, π, r 3, , ( ), , ( , √3 ), 3, 2, , r (0), , C, 1, , π, r 3, , 0, , r(0), , ( ), , EXAMPLE 2 Find the tangent vectors to the plane curve C defined by the vector function r(t) � 3 cos ti � 2 sin tj at the points where t � 0 and t � p>3. Make a sketch, of C, and display the position vectors r(0) and r(p>3) and the tangent vectors r¿(0), and r¿(p>3)., Solution, , The tangent vector to the curve C at any point is given by, , (3, 0) x, , �2, , FIGURE 2, The vectors r¿(0) and r¿(p>3) are tangent to the curve at the points (3, 0), and 1 32, 13 2 , respectively., , r¿(t) � �3 sin ti � 2 cos tj, In particular, the tangent vectors at the points where t � 0 and t � p>3 are, r¿(0) � 2j, , and, , p, 313, r¿a b � �, i�j, 3, 2, , These vectors are shown emanating from their points of tangency at (3, 0) and, in Figure 2., , 1 32, 13 2, , EXAMPLE 3 Find parametric equations for the tangent line to the helix with parametric equations, x � 3 cos t, , y � 2 sin t, , z�t, , at the point where t � p>6., Solution, , The vector function that describes the helix is, r(t) � 3 cos ti � 2 sin tj � tk, , The tangent vector at any point on the helix is, r¿(t) � �3 sin ti � 2 cos tj � k, In particular, the tangent vector at the point, , p, 1 313, 2 , 1, 6 2 , where t � p>6, is, , p, 3, r¿a b � � i � 13j � k, 6, 2, , p, Finally, we observe that the required tangent line passes through the point 1 313, 2 , 1, 6 2, and has the same direction as the tangent vector r¿(p>6). Using Equation (1) of Section 11.5, we see that the parametric equations of this line are, , x�, , 313, 3, � t,, 2, 2, , y � 1 � 13t,, , and, , z�, , p, �t, 6, , Higher-Order Derivatives, Higher-order derivatives of vector functions are obtained by successive differentiation, of the lower-order derivatives of the function. For example, the second derivative of, r(t) is, r⬙(t) �, , d, r¿(t) � f ⬙(t)i � t⬙(t)j � h⬙(t)k, dt, , EXAMPLE 4 Find r⬙(t) if r(t) � 2e3t i � ln tj � sin tk., Solution, , We have, r¿(t) � 6e3t i �, , 1, j � cos tk, t
Page 12 :
12.2, , Differentiation and Integration of Vector-Valued Functions, , 995, , and, r⬙(t) � 18e3t i �, , 1, t2, , j � sin tk, , Rules of Differentiation, The following theorem gives the rules of differentiation for vector functions. As you, might expect, some of the rules are similar to the differentiation rules of Chapter 2., , THEOREM 2 Rules of Differentiation, Suppose that u and v are differentiable vector functions, f is a differentiable realvalued function, and c is a scalar. Then, 1., 2., 3., 4., 5., 6., , d, dt, d, dt, d, dt, d, dt, d, dt, d, dt, , [u(t) � v(t)] � u¿(t) � v¿(t), [cu(t)] � cu¿(t), [ f(t)u(t)] � f ¿(t)u(t) � f(t)u¿(t), [u(t) ⴢ v(t)] � u¿(t) ⴢ v(t) � u(t) ⴢ v¿(t), [u(t), , v(t)] � u¿(t), , v(t) � u(t), , [u( f(t))] � u¿( f(t))f ¿(t), , v¿(t), , Chain Rule, , We will prove Rule 4 and leave the proofs of the other rules as exercises., , PROOF Let, u(t) � f1 (t)i � t1 (t)j � h 1 (t)k, , and, , v(t) � f2(t)i � t2 (t)j � h 2 (t)k, , Then, u(t) ⴢ v(t) � f1(t)f2(t) � t1(t)t2 (t) � h 1 (t)h 2 (t), Therefore, d, [u(t) ⴢ v(t)] � [f 1œ (t)f2(t) � t1œ (t)t2 (t) � h 1œ (t)h 2 (t)], dt, � [f1(t)f 2œ (t) � t1(t)t2œ (t) � h 1(t)h 2œ (t)], � u¿(t) ⴢ v(t) � u(t) ⴢ v¿(t), , EXAMPLE 5 Suppose that v is a differentiable vector function of constant length c., Show that v ⴢ v¿ � 0. In other words, the vector v and its tangent vector v¿ must be, orthogonal., Solution, , The condition on v implies that, v ⴢ v � 冟 v 冟2 � c2
Page 14 :
12.2, , Differentiation and Integration of Vector-Valued Functions, , 997, , where C1, C2, and C3 are constants of integration. We can rewrite the last expression as, 1, 1, 1, a t 2 � tbi � sin 2tj � e3t k � C1i � C2 j � C3k, 2, 2, 3, or, upon letting C � C1i � C2 j � C3k,, , 冮 r(t) dt � a 2 t, 1, , 2, , � tbi �, , 1, 1, sin 2tj � e3t k � C, 2, 3, , where C is a constant (vector) of integration., Note, , In general, the indefinite integral of r can be written as, , 冮 r(t) dt � R(t) � C, where C is an arbitrary constant vector and R¿(t) � r(t)., , EXAMPLE 8 Find the antiderivative of r¿(t) � cos ti � e�tj � 1tk satisfying the, , initial condition r(0) � i � 2j � 3k., Solution, , We have, , 冮 r¿(t) dt � 冮 (cos ti � e, , r(t) �, , �t, , j � t 1>2 k) dt, , 2 3>2, t k�C, 3, , � sin ti � e�tj �, , where C is a constant (vector) of integration. To determine C, we use the condition, r(0) � i � 2j � 3k to obtain, r(0) � 0i � j � 0k � C � i � 2j � 3k, from which we find C � i � 3j � 3k. Therefore,, 2 3>2, t k � i � 3j � 3k, 3, 2, � (1 � sin t)i � (3 � e�t)j � a3 � t 3>2 bk, 3, , r(t) � sin ti � e�tj �, , 1, , EXAMPLE 9 Evaluate, , 冮 r(t) dt if r(t) � t i � t � 1 j � e, 1, , 2, , �t, , k., , 0, , Solution, , 冮, , 1, , 1, , r(t) dt �, , 0, , 冮 at i � t � 1 j � e, 2, , 1, , �t, , kb dt, , 0, , �c, , 冮, , 0, , 1, , t 2dtdi � c, , 冮, , 0, , 1, , 1, dtd j � c, t�1, , 1, , 冮e, , �t, , 0, , 1 1, 1, 1, � c t 3 d i � Cln(t � 1) D 0 j � C�e�t D 0 k, 3 0, �, , 1, 1, i � ln 2j � a1 � bk, e, 3, , dtdk
Page 15 :
998, , Chapter 12 Vector-Valued Functions, , 12.2, , CONCEPT QUESTIONS, 3. Let r(t) � f(t)i � t(t)j � h(t)k., a. What is the indefinite integral of r with respect to t?, b. What is the definite integral of r over the interval [a, b]?, , 1. a. What is the derivative of a vector function?, b. If r(t) � f(t)i � t(t)j � h(t)k, what is r¿(t)?, c. Give an example of a function r(t) such that r¿(0) does, not exist., 2. If w(t) � u( f(t)) v( f(t)) , what is w¿(t) ? Assume that u, v,, and f are all differentiable., , 12.2, , EXERCISES, 20. r(t) � t sin ti � t cos tj � tk; t �, , In Exercises 1–8, find r¿(t) and r⬙(t)., 1. r(t) � ti � t 2j � t 3 k, , In Exercises 21–26, find parametric equations for the tangent, line to the curve with the given parametric equations at the point, with the indicated value of t., , 1, j � ln tk, t, , 2. r(t) � 1t i �, , 3. r(t) � 具t 2 � 1, 2t 2 � 1典, 5. r(t) � 具t cos t � sin t, t sin t � cos t典, 7. r(t) � e�t sin ti � e�t cos tj � tan�1 tk, 8. r(t) � 具sin�1 t, sec t, ln 冟 t 冟典, In Exercises 9–16, (a) find r(a) and r¿(a) at the given value of a., (b) Sketch the curve defined by r and the vectors r(a) and r¿(a), on the same set of axes., , 10. r(t) � sin ti � cos tj;, , a�2, , 12. r(t) � t 2i � t 3j;, , p, 3, , 14. r(t) � 具e , e, , p, 4, , 25. x � t cos t, y � t sin t, z � tet; t �, , p, 6, , 27., , 冮 (ti � 2t j � 3k) dt, , 28., , 冮 (ti � t j � t k) dt, , a�1, , 29., , 典; a � 0, 30., , p, a�, 4, , 16. r(t) � b cos3 ti � b sin3 tj;, , 2, , 3, , a�, , p, 4, , t�1, , 18. r(t) � 具e , te , (t � 1)e 典;, 2t, , 冮 a 1t i � t j � t, 1, , 冮, , 2, , 1, , In Exercises 17–20, find the unit tangent vector T(t) at the point, corresponding to the given value of the parameter t., �t, , 2, , 1, , �2t, , 17. r(t) � ti � 2tj � 3tk;, , y � t 2, z � 2 sin t;, , 26. x � e�t cos t, y � e�t sin t, z � sin�1t; t � 0, , a�1, , 15. r(t) � sec ti � 2 tan tj;, , t, , t�, , 24. x � 2 cos t,, , 0, , 13. r(t) � (2 � 3t)i � (1 � 2t)j;, t, , 1, 2, , z� 2, ; t�2, t�1, t �4, , In Exercises 27–34, find or evaluate the integral., , p, 4, , 11. r(t) � 具4 cos t, 2 sin t典; a �, , t�1, , 22. x � 1 � t, y � t 2 � 4, z � 1t; t � 4, 23. x � 1t � 2, y �, , 6. r(t) � e�t i � tet j � e�2t k, , a�, , z � t 3;, , 21. x � t, y � t 2,, , 4. r(t) � 具t cos t, t sin t, tan t典, , 9. r(t) � 1t i � (t � 4)j;, , p, 2, , t�0, , c 1t � 1 i �, , 3>2, , kb dt, , 1, j � (2t � 1)5 kd dt, 1t, , 31., , 冮 (sin 2ti � cos 2tj � e, , 32., , 冮 (te i � 2j � sec, , 33., , 冮 (t cos ti � t sin t j � te k) dt, , 34., , 冮 c1 � t, , p, 19. r(t) � 2 sin 2ti � 3 cos 2tj � 3k; t �, 6, , V Videos for selected exercises are available online at www.academic.cengage.com/login., , t, , 2, , 2, , i�, , k) dt, , tk) dt, , 2, , 1, , �t, , t, 1 � 2t 2, , t2, , j�, , 1, 21 � t 2, , kd dt
Page 16 :
12.2, In Exercises 35–40, find r(t) satisfying the given conditions., 35. r¿(t) � 2i � 4tj � 6t k;, , d, [r(t) ⴢ (u(t) v(t))], dt, � r¿(t) ⴢ [u(t) v(t)] � r(t) ⴢ [u¿(t), , 1, 36. r¿(t) � 2 sin 2ti � 3 cos 2tj � tk; r(0) � i � 2j � k, 2, �t, , � r(t) ⴢ [u(t), , 37. r¿(t) � 2e i � 3e j � e k; r(0) � i � j � k, 2t, , 999, , 54. Prove that, , r(0) � i � k, , 2, , Differentiation and Integration of Vector-Valued Functions, , t, , v(t)], , v¿(t)], , 1, k; r(3) � i � j � 2k, t, , In Exercises 55–58, find the indicated derivative., , r¿(0) � i � k,, , 55., , d, 1, cr(�t) � ra b d, dt, t, , 56., , d, [r(2t) ⴢ r(t 2)], dt, , In Exercises 41–46, let u(t) � t 2i � 2tj � 2k,, v(t) � cos ti � sin tj � t 2k, and f(t) � e2t., , 57., , d, [r(t) ⴢ (r¿(t), dt, , 41. Show that, , d, [u(t) � v(t)] � u¿(t) � v¿(t)., dt, , 58., , d, {u(t), dt, , 42. Show that, , d, [3u(t)] � 3u¿(t)., dt, , In Exercises 59 and 60, suppose that u and v are integrable on, [a, b] and that c is a scalar. Prove each property., , 43. Show that, , d, [ f(t)u(t)] � f ¿(t)u(t) � f(t)u¿(t)., dt, , 59., , 38. r¿(t) � 1t � 1 i �, , t, t2 � 1, , j�, , 39. r⬙(t) � 1t i � sec2 tj � et k;, r(0) � 2i � j � k, , 40. r⬙(t) � 3 cos 2ti � 4 sin 2tj � k;, r(0) � 2i � j � k, , r¿(0) � i � 2j,, , r⬙(t))], , [v(t), , w(t)]}, , b, , b, , b, , 冮 [u(t) � v(t)] dt � 冮 u(t) dt � 冮 v(t) dt, a, , a, , b, , a, , b, , 冮 cu(t) dt � c冮 u(t) dt, , 44. Show that, , d, [u(t) ⴢ v(t)] � u¿(t) ⴢ v(t) � u(t) ⴢ v¿(t)., dt, , 60., , 45. Show that, , d, [u(t), dt, , 61. a. Suppose that r is integrable on [a, b] and that c is a constant vector. Prove that, , v(t)] � u¿(t), , v(t) � u(t), , v¿(t)., , a, , a, , 冮, , d, 46. Show that [u( f(t))] � u¿[ f(t)]f ¿(t) ., dt, , b, , b, , c ⴢ r(t) dt � c ⴢ, , a, , a, , b. Verify this property directly for the vector function, , In Exercises 47–52, suppose u and v are differentiable vector, functions, f is a differentiable real-valued function, and c is a, scalar. Prove each rule., d, [u(t) � v(t)] � u¿(t) � v¿(t), 47., dt, , r(t) � sin ti � cos tj � tk,, c � 2i � 3j � k,, , and, , d, [u(t) � v(t)] � u¿(t) � v¿(t), dt, , 49., , d, [cu(t)] � cu¿(t), dt, , 62. If c is a constant vector, then, , 50., , d, [ f(t)u(t)] � f ¿(t)u(t) � f(t)u¿(t), dt, , 63., , 51., , d, [u(t), dt, , v(t) � u(t), , v¿(t), , d, [r(t), dt, , r¿(t)] � r(t), , b�p, , d, (c) � 0., dt, , d, (冟 u 冟2) � 2u ⴢ u¿, dt, , 64. If r¿(t) � 0, then r(t) � c, where c is an arbitrary constant, vector., 65. If r is differentiable and r(t) ⴢ r¿(t) � 0 for all t, then r must, have constant length., , d, [u( f(t))] � u¿( f(t))f ¿(t), 52., dt, 53. Prove that, , a � 0,, , In Exercises 62–65, determine whether the statement is true or, false. If it is true, explain why. If it is false, explain why or give, an example to show that it is false., , 48., , v(t)] � u¿(t), , 冮 r(t) dt, , r⬙(t).
Page 17 :
1000, , Chapter 12 Vector-Valued Functions, , 12.3 Arc Length and Curvature, Arc Length, In Section 10.3 we saw that the length of the plane curve given by the parametric equations x � f(t) and y � t(t), where a � t � b, is, L�, , 冮, , b, , a, , dy 2, dx 2, b � a b dt �, B dt, dt, a, , b, , 冮 2[ f ¿(t)], , 2, , � [t¿(t)]2 dt, , a, , Now, suppose that C is described by the vector function r(t) � f(t)i � t(t)j, instead. Then, r¿(t) � f ¿(t)i � t¿(t)j, and, 冟 r¿(t) 冟 � 2r¿(t) ⴢ r¿(t) � 2[ f ¿(t)]2 � [t¿(t)]2, from which we see that L can also be written in the form, b, , L�, , 冮 冟 r¿(t) 冟 dt, a, , A similar formula for calculating the length of a space curve is contained in the following theorem., , THEOREM 1 Arc Length of a Space Curve, Let C be a curve given by the vector function, r(t) � f(t)i � t(t)j � h(t)k, , a�t�b, , where f ¿, t¿, and h¿ are continuous. If C is traversed exactly once as t increases, from a to b, then its length is given by, L�, , 冮, , b, , b, , 2[ f ¿(t)]2 � [t¿(t)]2 � [h¿(t)]2 dt �, , a, , z, , 冮 冟 r¿(t) 冟 dt, a, , EXAMPLE 1 Find the length of the arc of the helix C given by the vector function, r(t) � 2 cos ti � 2 sin tj � tk, where 0 � t � 2p, as shown in Figure 1., Solution, , We first compute, r¿(t) � �2 sin ti � 2 cos tj � k, , C, , Then, using Theorem 1, we see that the length of the arc in question is, y, , x, , FIGURE 1, The length of the arc of the helix, for 0 � t � 2p is 2 15p., , L�, , 冮, , 2p, , 冮, , 2p, , 冟 r¿(t) 冟 dt �, , 0, , �, , 冮, , 2p, , 24 sin2 t � 4 cos2 t � 1 dt, , 0, , 0, , 15 dt � 215p
Page 18 :
12.3, y, , Arc Length and Curvature, , 1001, , Smooth Curves, , Cusp, , x, , FIGURE 2, The curve defined by r(t) � t 3i � t 2 j, is smooth everywhere except at (0, 0)., , A curve that is defined by a vector function r on a parameter interval I is said to be, smooth if r¿(t) is continuous and r¿(t) 0 for all t in I with the possible exception of, the endpoints. For example, the plane curve defined by r(t) � t 3 i � t 2 j is smooth, everywhere except at the point (0, 0) corresponding to t � 0. To see this, we compute, r¿(t) � 3t 2 i � 2tj and note that r¿(0) � 0. The curve is shown in Figure 2. The point, (0, 0) where the curve has a sharp corner is called a cusp., , Arc Length Parameter, The curve C described by the vector function r(t) with parameter t in some parameter, interval I is said to be parametrized by t. A curve C can have more than one parametrization. For example, the helix represented by the vector function, r1(t) � 2 cos ti � 3 sin tj � tk, , 2p � t � 4p, , with parameter t is also represented by the function, r2 (u) � 2 cos eu i � 3 sin eu j � eu k, , ln 2p � u � ln 4p, , with parameter u, where t and u are related by t � eu., A useful parametrization of a curve C is obtained by using the arc length of C as, its parameter. To see how this is done, we need the following definition., , DEFINITION Arc Length Function, Suppose that C is a smooth curve described by r(t) � f(t)i � t(t)j � h(t)k,, where a � t � b. Then the arc length function s is defined by, t, , s(t) �, , 冮 冟 r¿(u) 冟 du, , (1), , a, , Thus, s(t) is the length of that part of C (shown in red) between r(a) and r(t) . (See, Figure 3.) Because s(a) � 0, we see that the length L of C from t � a to t � b is, b, , s(b) �, , 冮 冟 r¿(t) 冟 dt, a, , z, , C, , r(b), , r(t), , FIGURE 3, The arc length function s(t) gives the, length of that part of C corresponding, to the parameter interval [a, t]., , r(a), [, a, , t, , ], b, , Parameter interval, , 0, t, , y, x
Page 19 :
1002, , Chapter 12 Vector-Valued Functions, , If we differentiate both sides of Equation (1) with respect to t and use the Fundamental Theorem of Calculus, Part 2, we obtain, ds, � 冟 r¿(t) 冟, dt, , (2), , ds � 冟 r¿(t) 冟 dt, , (3), , or, in differential form,, , The following example shows how to parametrize a curve in terms of its arc length., , EXAMPLE 2 Find the arc length function s(t) for the circle C in the plane described, by, r(t) � 2 cos ti � 2 sin tj, , 0 � t � 2p, , Then use your result to find a parametrization of C in terms of s., Solution, , We first compute r¿(t) � �2 sin ti � 2 cos tj, and then compute, 冟 r¿(t) 冟 � 24 sin2 t � 4 cos2 t � 2, , Using Equation (1), we obtain, s(t) �, , 冮, , t, , 冟 r¿(u) 冟 du �, , 0, , t, , 冮 2 du � 2t, , 0 � t � 2p, , 0, , Writing s for s(t), we have s � 2t, where 0 � t � 2p, which when solved for t, yields, t � t(s) � s>2. Substituting this value of t into the equation for r(t) gives, s, s, r(t(s)) � 2 cosa bi � 2 sina bj, 2, 2, Finally, since s(0) � 0 and s(2p) � 4p, we see that the parameter interval for this, parametrization by the arc length s is [0, 4p]. (See Figure 4.), y, , FIGURE 4, The curve C is described by, r(t) � 2 cos ti � 2 sin tj,, where 0 � t � 2p, and, r(t(s)) � 2 cos(s>2)i � 2 sin(s>2)j,, where 0 � s � 4p., , C, [, 0, , ], 2π, , �2, , 2, , x, , [, 0, , t, , Parameter interval for r(t), , ], 4π, , s, , Parameter interval for r(s), , One reason for using the arc length of a curve C as the parameter stems from the, fact that its tangent vector r¿(s) has unit length; that is, r¿(s) is a unit tangent vector., Consider the circle of Example 2. Here,, s, s, r¿(s) � �sina bi � cosa bj, 2, 2, so, 冟 r¿(s) 冟 �, , B, , s, s, sin2 a b � cos2 a b � 1, 2, 2
Page 20 :
12.3, z, , Arc Length and Curvature, , 1003, , Curvature, , C, 0, y, x, , FIGURE 5, The unit tangent vector T(s) turns, faster along the stretch of the path, where the turn is sharper., , Figure 5 depicts the flight path C of an aerobatic plane as it executes a maneuver. Suppose that the smooth curve C is defined by the vector function r(s), where s is the arc, length parameter. Then the unit tangent vector function T(s) � r¿(s) gives the direction of the plane at the point on C corresponding to the parameter value s., In Figure 5 we have drawn the unit tangent vector T(s) to C corresponding to several values of s. Observe that T(s) turns rather slowly along a stretch of the flight path, that is relatively straight but turns more quickly along a stretch of the curve where the, plane executes a sharp turn., To measure how quickly a curve bends, we introduce the notion of the curvature, of a curve. Specifically, we define the curvature at a point on a curve C to be the magnitude of the rate of change of the unit tangent vector with respect to arc length at that, point., , DEFINITION Curvature, Let C be a smooth curve defined by r(s), where s is the arc length of the parameter. Then the curvature of C at s is, k(s) � `, , dT, ` � 冟 T¿(s) 冟, ds, , where T is the unit tangent vector., , Note, , The Greek letter k is read “kappa.”, , Although the use of the arc length parameter s provides us with a natural way for, defining the curvature of a curve, it is generally easier to find the curvature in terms, of the parameter t. To see how this is done, let’s apply the Chain Rule (Rule 6 in Section 12.2) to write, dT, dT ds, �, dt, ds dt, Then, dT, `, `, dT, dt, `�, k(s) � `, ds, ds, ` `, dt, Since ds>dt � 冟 r¿(t) 冟 by Equation (2), we are led to the following formula:, k(t) �, , 冟 T¿(t) 冟, 冟 r¿(t) 冟, , (4), , EXAMPLE 3 Find the curvature of a circle of radius a., Solution Without loss of generality we may take the circle C with center at the origin. This circle is represented by the vector function, r(t) � a cos ti � a sin tj, , 0 � t � 2p
Page 21 :
1004, , Chapter 12 Vector-Valued Functions, , Now, r¿(t) � �a sin ti � a cos tj, so, 冟 r¿(t) 冟 � 2a 2 sin2 t � a 2 cos2 t � a, Therefore,, T(t) �, , r¿(t), � �sin ti � cos tj, 冟 r¿(t) 冟, , Next, we compute, T¿(t) � �cos ti � sin tj, and, 冟 T¿(t) 冟 � 2cos2 t � sin2 t � 1, Finally, using Equation (4), we obtain, 冟 T¿(t) 冟, 1, �, 冟 r¿(t) 冟, a, , k(t) �, , Therefore, the curvature at every point on the circle of radius a is 1>a. This result, agrees with our intuition: A big circle has a small curvature and vice versa., The following formula expresses the curvature in terms of the vector function r and, its derivatives., , THEOREM 2 Formula for Finding Curvature, Let C be a smooth curve given by the vector function r. Then the curvature of, C at any point on C corresponding to t is given by, k(t) �, , 冟 r¿(t), , r⬙(t) 冟, 冟 r¿(t) 冟3, , PROOF We begin by recalling that, T(t) �, , r¿(t), 冟 r¿(t) 冟, , Since 冟 r¿(t) 冟 � ds>dt, we have, r¿(t) �, , ds, T(t), dt, , Differentiating both sides of this equation with respect to t and using Rule 3 in Section 12.2, we obtain, r⬙(t) �, , d 2s, dt, , 2, , T(t) �, , ds, T¿(t), dt
Page 23 :
1006, , Chapter 12 Vector-Valued Functions, , If a plane curve C happens to be contained in the graph of a function defined by, y � f(x), then we can use the following formula to compute its curvature., , THEOREM 3 Formula for the Curvature of the Graph of a Function, If C is the graph of a twice differentiable function f, then the curvature at the, point (x, y) where y � f(x) is given by, k(x) �, , 冟 f ⬙(x) 冟, [1 � [f ¿(x)] ], , 2 3>2, , �, , 冟 y⬙ 冟, , (5), , [1 � (y¿)2]3>2, , PROOF Using x as the parameter, we can represent C by the vector function r(x) �, xi � f(x)j � 0k. Differentiating r(x) with respect to x successively, we obtain, r¿(x) � i � f ¿(x)j � 0k, , r⬙(x) � 0i � f ⬙(x)j � 0k, , and, , from which we obtain, r¿(x), , i, r⬙(x) � † 1, 0, , j, f ¿(x), f ⬙(x), , k, 0 † � f ⬙(x)k, 0, , and, 冟 r¿(x), , r⬙(x) 冟 � 冟 f ⬙(x) 冟, , Also,, 冟 r¿(x) 冟 � 21 � [f ¿(x)]2, Therefore,, k(x) �, , 冟 r¿(x), , 冟 f ⬙(x) 冟, r⬙(x) 冟, �, 3, 冟 r¿(x) 冟, [1 � [f ¿(x)]2]3>2, , EXAMPLE 5, a. Find the curvature of the parabola y � 14 x 2 at the points where x � 0 and x � 1., b. Find the point(s) where the curvature is largest., Solution, a. We first compute y¿ � 12 x and y⬙ � 12. Then using Theorem 3, we find the curvature at any point (x, y) on the parabola y � 12 x 2 to be, k(x) �, , 冟 y⬙ 冟, [1 � (y¿) ], , 2 3>2, , �, , 11 �, , 1, 2, 1 2 3>2, 4x, , 2, , �, , 4, (4 � x 2)3>2, , In particular, the curvature at the point (0, 0) , where x � 0, is, 4, , k(0) �, , (4 � x ), , 2 3>2, , `, , �, x�0, , and the curvature at the point 1 1, 2 , where x � 1, is, , 1, 2, , 1, 4, , k(1) �, , 4, , (4 � x ), , 2 3>2, , `, , �, x�1, , 4, , 53>2, , ⬇ 0.358
Page 24 :
12.3, , b. To find the value of x at which k is largest, we compute, , y, 4, , k¿(x) �, , 3, , 1, �2, , d, 12x, [4(4 � x 2)�3>2] � �6(4 � x 2)�5>2 (2x) � �, dx, (4 � x 2)5>2, , Setting k¿(x) � 0 yields the sole critical point x � 0. We leave it to you to show, that x � 0 does give the absolute maximum value of k(x)., , 2, , �4, , 1007, , Arc Length and Curvature, , 0, , 2, , FIGURE 6, The graph of y � 14 x 2, , 4, , x, , The graph of y � 14 x 2 is shown in Figure 6., , Radius of Curvature, Suppose that C is a plane curve with curvature k at the point P. Then the reciprocal of, the curvature, r � 1>k, is called the radius of curvature of C at P. The radius of curvature at any point P on a curve C is the radius of the circle that best “fits” the curve, at that point. This circle, which lies on the concave side of the curve and shares a common tangent line with the curve at P, is called the circle of curvature or osculating, circle. (See Figure 7.), The center of the circle is called the center of curvature. As an example, the curvature of the parabola y � 14 x 2 of Example 5 at the point (0, 0) was found to be 12., Therefore, the radius of curvature of the parabola at (0, 0) is r � 1>(1/2) � 2. The circle of curvature is shown in Figure 8. Its equation is x 2 � (y � 2)2 � 4., y, , y, C, P, ®, , 3, 2, 1, , 0, , x, , FIGURE 7, The radius of curvature at P is the, radius of the circle that best fits the, curve C at P., , 12.3, , �4, , �2, , 0, , 2, , 4, , x, , FIGURE 8, The circle of curvature is tangent to the, parabola., , CONCEPT QUESTIONS, , 1. Give the formula for finding the arc length of the curve C, defined by r(t) � 具 f(t), t(t), h(t)典 for a � t � b. What condition, if any, must be imposed on C?, 2. a. What is a smooth curve?, b. Give an example of a curve in 3-space that is not, smooth., 3. a. What is the arc length function associated with, r(t) � 具 f(t), t(t), h(t)典, where a � t � b?, b. If a curve is parametrized in terms of its arc length, what, is the unit tangent vector T(s)? What is T(t), where t is, not the arc length parameter?, , 4. a. What is the curvature of a smooth curve C at s, where s, is the arc length parameter?, b. If t is not the arc length parameter, what is the curvature, of C at t?, c. What is the radius of curvature of a curve C at a point P, on C ?
Page 25 :
1008, , Chapter 12 Vector-Valued Functions, , 12.3, , EXERCISES, In Exercises 29–32, find the point(s) on the curve at which the, curvature is largest., , In Exercises 1–8, find the length of the curve., 1. r(t) � ti � 2tj � 3tk, 0 � t � 4, 2. r(t) � 具5t, 3t 2, 4t 2典,, , 0�t�2, , 3. r(t) � 4 sin ti � 3tj � 4 cos tk,, , 0 � t � 2p, , 4. r(t) � a cos ti � a sin tj � btk, 0 � t � 2p, 5. r(t) � 具et cos t, et sin t, et典,, , 0 � t � 2p, , 6. r(t) � t 2 i � t cos tj � t sin tk,, 7. r(t) � 2ti � t j � ln tk,, 2, , 0�t�1, , 29. y � ex, , 30. y � ln x, , 31. xy � 1, , 32. 4x 2 � 9y 2 � 36, , In Exercises 33–36, match the curve with the graph of its curvature y � k(x) in (a)–(d)., 33., , 1�t�e, , 8. r(t) � (cos t � t sin t)i � (sin t � t cos t)j � t 2 k,, 0 � t � p2, In Exercises 9 and 10, use a calculator or computer to graph the, curve represented by r(t), and find the length of the curve for t, defined on the indicated interval., 9. r(t) � t sin ti � t cos tj � tk;, , 10. r(t) � 2 sin ti � 2 cos tj � 12 t 2 k;, , �4, , �2, , 13. r(t) � e cos ti � e sin tj � e k,, , t�0, , 14. r(t) � a cos3 ti � a sin3 tj � k,, , 0 � t � p2, , t, , t, , 36., , �1, , (a), , 0, , 2 x, , 1, , �4, , �2, , (b), , y, , 0, , 4 x, , 2, , 4 x, , y, 1.0, 0.8, 0.6, 0.4, , �2 �1 0, , 18. r(t) � (1 � t)i � (1 � t)j � 3t 2 k, , (c), , 1, , 2, , x, , 20. r(t) � 具et cos t, et sin t, et典, In Exercises 21–26, use Theorem 3 to find the curvature of the, curve., , �4, (d), , y, , 19. r(t) � 2 sin ti � 2 cos tj � 2tk, , 24. y � ln x, , 2, , 4, , 2, , 17. r(t) � ti � 12 t 2 j � t 2 k, , 23. y � sin 2x, , 10 x, , 3, , 16. r(t) � ti � j � t 2 k, , 22. y � x 4, , 5, , y, 8, , 1, , 21. y � x 3 � 1, , 0, , 1, �2, , 15. r(t) � 2ti � 2tj � k, , 25. y � e, , 4 x, , 2, , 1, , In Exercises 15–20, use Theorem 2 to find the curvature of the, curve., , �x2, , 1, , 0, , 2, , t�0, t�0, , t, , 2, , 3, , In Exercises 11–14, find the arc length function s(t) for the curve, defined by r(t). Then use this result to find a parametrization of, C in terms of s., 12. r(t) � 4 sin ti � 4 cos tj � 3tk,, , 3, , y, , [0, 2p], , 11. r(t) � (1 � t)i � (1 � 2t)j � 3tk,, , y, 4, , �10 �5, , 35., , [0, 2p], , 34., , y, 5, 4, 3, 2, 1, , �2, , 0, y, , 8, , 8, , 6, , 6, , 4, , 4, , 2, �3 �2 �1 0, , 26. y � sec x, , 1, , 2, , 3 x, , �3 �2 �1 0, , 1, , 2, , 3 x, , 2, , 27. Find the point(s) on the graph of y � e�x at which the, curvature is zero., 28. Find an equation of the circle of curvature for the graph of, f(x) � x � (1>x) at the point (1, 2) . Sketch the graph of f, and the circle of curvature., , In Exercises 37 and 38, find the curvature function k(x) of the, curve. Then use a calculator or computer to graph both the, curve and its curvature function k(x) on the same set of axes., 37. y � e�x, , V Videos for selected exercises are available online at www.academic.cengage.com/login., , 2, , 38. y � ln(1 � x 2)
Page 26 :
12.3, 39. Suppose that C is a smooth curve with parametric equations, x � f(t), y � t(t). Using Theorem 2, show that the curvature, at the point (x, y) corresponding to any value of t is, k(t) �, , Arc Length and Curvature, , 1009, , of cornu makes the curve useful in highway design: It provides, a gradual transition from a straight road (zero curvature) to a, curved road (with positive curvature), such as an exit ramp., , 冟 f ¿(t)t⬙(t) � t¿(t)f ⬙(t) 冟, , y, , {[f ¿(t)]2 � [t¿(t)]2}3>2, , In Exercises 40 and 41, use the formula in Exercise 39 to find, the curvature of the curve., 40. x � cos t,, , y � t sin t, , 41. x � t � sin t,, , x, , y � 1 � cos t, , 42. a. The curvature of the curve C at P shown in the figure is, 2. Sketch the osculating circle at P. (Use the tangent line, shown at P as an aid.), b. What is the curvature of C at Q?, 46. Suppose that the curve C is described by a polar equation, r � f(u). Show that the curvature at the point (r, u) is, given by, , y, 5, 8 in., , P, , k(u) �, , C, , 冟 2(r¿)2 � rr ⬙ � r 2 冟, [(r¿)2 � r 2]3>2, , Hint: Represent C by r(u) � r cos ui � r sin uj., Q, 0, , x, , 43. a. Find the curvature at the point (x, y) on the ellipse, , x � a cos t, , b. Find the curvature and the equation of the osculating, circle at the points (3, 0) and (0, 2)., c. Sketch the graph of the ellipse and the osculating circles, of part (b)., 44. Find the curvature k(t) for the curve with parametric, equations, , What happens to k(t) as t approaches 0?, Note: The curve is not smooth at t � 0., , 45. The spiral of cornu is defined by the parametric equations, x�, , 冮, , 0, , t, , cosa, , pu 2, b du, 2, , y�, , 48. r � eu, , 冮, , t, , 0, , sina, , y � a sin t, , z � bt, , where a � 0, is given by k(t) � a>(a � b 2)., 2, , 50. Find the curvature at the point (x, y, z) on an elliptic helix, with parametric equations, x � a cos t, , y � b sin t, , where a, b, and c are positive and a, , z � ct, b., , 51. Find the arc length of r(t) � t cos ti � t sin tj � tk, where, 0 � t � 2p., , y � t3, , and, , 47. r � 1 � sin u, , 49. Show that the curvature at every point on the helix, , y2, x2, �, �1, 9, 4, , x � t2, , In Exercises 47 and 48, use the formula in Exercise 46 to find, the curvature of the curve., , pu 2, b du, 2, , and was encountered in Exercise 45 of Section 10.3. Its, graph follows., dy, d 2y, a. Find, and 2 ., dx, dx, b. Find the curvature of the spiral., Note: The curvature k(t) increases from 0 at a constant rate with, respect to t as t increases from t � 0. This property of the spiral, , 52. Find the curvature of the graph of x 3 � y 3 � 9xy (folium, of Descartes) at the point (2, 4) accurate to four decimal, places., In Exercises 53–58, determine whether the statement is true or, false. If it is true, explain why. If it is false, explain why or give, an example to show that it is false., 53. If C is a smooth curve in the xy-plane defined by, r(t) � x(t)i � y(t)j on a parameter interval I, then, dy>dx is defined at every point on the curve., 54. The curve defined by r(t) � 具t, 冟 t 冟典 is smooth.
Page 27 :
1010, , Chapter 12 Vector-Valued Functions, 57. The radius of curvature of the plane curve y � 2a 2 � x 2 is, constant at each point on the curve., , 55. If the graph of a twice differentiable function f has an inflection point at a, then the curvature at the point (a, f(a)) is, zero., , 58. If r¿(t) is continuous for all t in an interval I, then r defines, a smooth curve., , 56. If C is the curve defined by the parametric equations, x � 1 � 2t, , y � 2 � 3t, , z � 4t, , then d T>ds � 0, where T is the unit tangent vector to C., , 12.4, , Velocity and Acceleration, Velocity, Acceleration, and Speed, The curve C in Figure 1 is the flight path of a fighter plane. We can represent C by the, vector function, r(t) � f(t)i � t(t)j � h(t)k, , t僆I, , where we think of the parameter interval I as a time interval and use r(t) to indicate, the position of the plane at time t., z, P, r (t), , FIGURE 1, The position vector r(t) gives, the position of a fighter plane at, time t, and its derivative r¿(t) gives, the plane’s velocity at time t., , C, [, a, , t, , ], b, , Parameter interval (time interval), , r(t), 0, , t, , y, x, , From Sections 12.2 and 12.3 we know that the vector r¿(t) has the following properties:, 1. r¿(t) is tangent to C at the point P corresponding to time t., ds, 2. 冟 r¿(t) 冟 � ., dt, Since ds>dt is the rate of change of the distance (measured along the arc) with respect, to time, it measures the speed of the plane. Thus, the vector r¿(t) gives both the speed, and the direction of the plane. In other words, it makes sense to define the velocity vector of the plane at time t to be r¿(t), the rate of change of its position vector with respect, to time. Similarly, we define the acceleration vector of the plane at time t to be r⬙(t),, the rate of change of its velocity vector with respect to time., To gain insight into the nature of the acceleration vector, let’s refer to Figure 2., Here, t is fixed, and h is a small number. The vector r¿(t) is tangent to the flight path, at the tip of the position vector r(t), and r¿(t � h) is tangent to the flight path at the, tip of r(t � h) . The vector, r¿(t � h) � r¿(t), h
Page 28 :
12.4, , Velocity and Acceleration, , 1011, , points in the general direction in which the plane is turning. Therefore, the acceleration vector, r⬙(t) �, , r¿(t � h) � r¿(t), d, r¿(t) � lim, dt, h→0, h, , points toward the concave side of the flight path as long as the direction of r¿(t) is, changing, in agreement with our intuition., z, , C, , r_______, (t � h) �____, r (t), h, , r (t � h), r (t � h) � r (t), , r(t � h), r (t), r(t), 0, , FIGURE 2, To find r¿(t � h) � r¿(t),, translate r¿(t � h) so that, its tail is at the tip of r(t)., , y, x, , Let’s summarize these definitions., , DEFINITIONS Velocity, Acceleration, and Speed, Let r(t) � f(t)i � t(t)j � h(t)k be the position vector of an object. If f, t, and, h are twice differentiable functions of t, then the velocity vector v(t), acceleration vector a(t), and speed 冟 v(t) 冟 of the object at time t are defined by, v(t) � r¿(t) � f ¿(t)i � t¿(t)j � h¿(t)k, a(t) � r⬙(t) � f ⬙(t)i � t⬙(t)j � h⬙(t)k, 冟 v(t) 冟 � 冟 r¿(t) 冟 � 2[ f ¿(t)]2 � [t¿(t)]2 � [h¿(t)]2, , EXAMPLE 1 The position of an object moving in a plane is given by, r(t) � t 2 i � tj, , t�0, , Find its velocity, acceleration, and speed when t � 2. Sketch the path of the object and, the vectors v(2) and a(2)., Solution, , The velocity and acceleration vectors of the object are, v(t) � r¿(t) � 2ti � j, , and, a(t) � r⬙(t) � 2i
Page 29 :
1012, , Chapter 12 Vector-Valued Functions, , Therefore, its velocity, acceleration, and speed when t � 2 are, v(2) � 4i � j, a(2) � 2i, , y, v(2), , and, 冟 v(2) 冟 � 116 � 1 � 117, , C, , 2, , a(2), , 1, 0, , 1, , 2, , 3, , x, , 4, , FIGURE 3, The path of the object C and the, vectors v(2) and a(2), , respectively., To sketch the path of the object, observe that the parametric equations of the curve, described by r(t) are x � t 2 and y � t. By eliminating t from these equations, we obtain, the rectangular equation x � y 2, where y � 0, which tells us that the path of the object, is contained in the graph of the parabola x � y 2. This path together with the vectors, v(2) and a(2) is shown in Figure 3., , EXAMPLE 2 Find the velocity vector, speed, and acceleration vector of an object that, moves along the plane curve C described by the position vector, y, , r(t) � 3 cos ti � 2 sin tj, , v(t), , 2, , Solution, , The velocity vector is, , a(t), �3, , 0, , v(t) � �3 sin ti � 2 cos tj, 3, , x, , The speed of the object at time t is, 冟 v(t) 冟 � 29 sin2 t � 4 cos2 t, , �2, , Finally, the acceleration vector is, FIGURE 4, The acceleration vector a points toward, the origin., , a(t) � �3 cos ti � 2 sin tj � �r(t), which shows the acceleration is directed toward the origin (see Figure 4)., , EXAMPLE 3 Find the velocity vector, acceleration vector, and speed of a particle, with position vector, r(t) � 1ti � t 2 j � e2t k, Solution, , t�0, , The required quantities are, v(t) � r¿(t) �, , 1 �1>2, 1, t, i � 2tj � 2e2t k �, i � 2tj � 2e2t k, 2, 21t, , 1, 1, a(t) � r⬙(t) � � t �3>2 i � 2j � 4e2t k � �, i � 2j � 4e2t k, 4, 42t 3, and, 冟 v(t) 冟 �, , 1, 21 � 16t 3 � 16te4t, � 4t 2 � 4e4t �, B 4t, 21t, , Suppose that we are given the velocity or acceleration vector of a moving object., Then it is possible to find the position vector of the object by integration, as is shown, in the next example.
Page 30 :
12.4, , Sueddeutsche Zeitung Photo/, The Image Works, , Historical Biography, , Velocity and Acceleration, , 1013, , EXAMPLE 4 A moving object has an initial position and an initial velocity given, by the vectors r(0) � i � 2j � k and v(0) � i � 2k. Its acceleration at time t is, a(t) � 6ti � j � 2k. Find its velocity and position at time t., Solution Since v¿(t) � a(t), we can obtain v(t) by integrating both sides of this equation with respect to t. Thus,, v(t) �, , HERMANN GÜNTHER GRASSMANN, , 冮 a(t) dt � 冮 (6ti � j � 2k) dt � 3t i � tj � 2tk � C, 2, , Letting t � 0 in this expression and using the initial condition v(0) � i � 2k, we obtain, , (1809–1877), A productive scholar whose work spanned, mathematics, linguistics, theology, and, botany, Hermann Günther Grassmann did, not focus his attention on mathematics, until the age of 31. As a student at the University of Berlin, he took courses in theology, classical languages, and literature, but, he appears not to have taken any courses, in mathematics or physics. After completing his university studies in 1830, Grassmann spent a year undertaking research in, mathematics and preparing himself to, teach in gymnasiums (secondary schools)., He did not do well on the exams and was, qualified to teach only at the lower levels., However, during this time he had made significant mathematical discoveries that, would eventually appear in his 1844 work, Die Lineale Ausdehnungslehre. This was a, truly groundbreaking work. In it he introduced many concepts and techniques that, are of central importance in contemporary, mathematics, such as n-dimensional vector, spaces and multilinear algebra. However,, this work was far ahead of its time, and, Grassmann’s writing style was not clear or, well polished. The mathematical community dismissed Die Lineale Ausdehnungslehre. In spite of this, Grassmann continued to work on his ideas about geometric, calculus and republished the paper in 1862., Still not understood by others, he turned, to studies in linguistics and other areas of, science. Before his death in 1877 he had, written a third version of his paper. It was, published after his death, and it was then, that Grassmann’s discoveries were recognized. Today, Grassmann is credited with, the invention of linear algebra., , v(0) � C � i � 2k, Therefore, the velocity of the object at any time t is, v(t) � (3t 2 i � tj � 2tk) � i � 2k, � (3t 2 � 1)i � tj � 2(t � 1)k, Next, integrating the equation r¿(t) � v(t) with respect to t gives, r(t) �, , 冮 v(t) dt � 冮 [(3t, , 2, , � 1)i � tj � 2(t � 1)k] dt, , � (t 3 � t)i �, , 1 2, t j � (t 2 � 2t)k � D, 2, , Letting t � 0 in r(t) and using the initial condition r(0) � i � 2j � k, we have, r(0) � D � i � 2j � k, Therefore, the position of the object at any time t is, r(t) � (t 3 � t)i �, , 1 2, t j � (t 2 � 2t)k � (i � 2j � k), 2, , 1, � (t 3 � t � 1)i � a t 2 � 2bj � (t 2 � 2t � 1)k, 2, 1, � (t 3 � t � 1)i � a t 2 � 2bj � (t � 1)2 k, 2, , Motion of a Projectile, A projectile of mass m is fired from a height h with an initial velocity v0 and an angle, of elevation a. If we describe the position of the projectile at any time t by the position vector r(t), then its initial position may be described by the vector, r(0) � hj, and its initial velocity by the vector, v(0) � v0 � (√0 cos a)i � (√0 sin a)j, (See Figure 5.), , √0 � 冟 v0 冟, , (1)
Page 31 :
1014, , Chapter 12 Vector-Valued Functions, y, , v0 � (√0 cos å)i � (√0 sin å)j, , √0 sin å, , å, , FIGURE 5, The initial position of the projectile, is r(0) � hj, and its initial velocity, is v0 � (√0 cos a)i � (√0 sin a)j., , h, , �mgj, , r(t), , √0 cos å, , r(0) � hj, x, , 0, , If we assume that air resistance is negligible and that the only external force acting on the projectile is due to gravity, then the force acting on the projectile during its, flight is, F � �mtj, where t is the acceleration due to gravity (32 ft/sec2 or 9.8 m/sec2). By Newton’s, Second Law of Motion this force is equal to ma, where a is the acceleration of the projectile. Therefore,, ma � �mtj, giving the acceleration of the projectile as, a(t) � �tj, To find the velocity of the projectile at any time t, we integrate the last equation with, respect to t to obtain, v(t) �, , 冮 �tj dt � �ttj � C, , Setting t � 0 and using the initial condition v(0) � v0, we obtain, v(0) � C � v0, Therefore, the velocity of the projectile at any time t is, v(t) � �ttj � v0, Integrating this equation then gives, r(t) �, , 冮 (�ttj � v ) dt � �2 tt j � v t � D, 1, , 2, , 0, , 0, , Setting t � 0 and using the initial condition r(0) � hj, we obtain, r(0) � D � hj, Therefore, the position of the projectile at any time t is, 1, r(t) � � tt 2 j � v0t � hj, 2, or, upon using Equation (1),, 1, r(t) � � tt 2 j � [(√0 cos a)i � (√0 sin a)j]t � hj, 2, � (√0 cos a)ti � ch � (√0 sin a)t �, , 1 2, tt d j, 2
Page 32 :
12.4, , Velocity and Acceleration, , 1015, , DEFINITION Position Function for a Projectile, The trajectory of a projectile fired from a height h with an initial speed √0 and, an angle of elevation a is given by the position vector function, r(t) � (√0 cos a)ti � ch � (√0 sin a)t �, , 1 2, tt d j, 2, , (2), , where t is the constant of acceleration due to gravity., , EXAMPLE 5 Motion of a Projectile A shell is fired from a gun located on a hill, 100 m above a level terrain. The muzzle speed of the gun is 500 m/sec, and its angle, of elevation is 30°., a. Find the range of the shell., b. What is the maximum height attained by the shell?, c. What is the speed of the shell at impact?, Solution Using Equation (2) with h � 100, √0 � 500, a � 30°, and t � 9.8, we see, that the position of the shell at any time t is given by, r(t) � (500 cos 30°)ti � [100 � (500 sin 30°)t � 4.9t 2]j, � 25013ti � (100 � 250t � 4.9t 2)j, The corresponding parametric equations are, x � 25013t, , and, , y � 100 � 250t � 4.9t 2, , a. We first find the time when the shell strikes the ground by solving the equation, 4.9t 2 � 250t � 100 � 0, obtained by setting y � 0. Using the quadratic formula, we have, t�, , 250 � 162,500 � 1960, ⬇ 51.4, 9.8, , We reject the, negative root., , or 51.4 sec. Substituting this value of t into the expression for x we find that the, range of the shell is approximately, 25013 (51.4) ⬇ 22,257, or 22,257 m., b. The height of the shell at any time t is given by, y � 100 � 250t � 4.9t 2, To find the maximum value of y, we solve, y¿ � 250 � 9.8t � 0, to obtain t ⬇ 25.5. Since y⬙ � �9.8 0, the Second Derivative Test implies that, at approximately 25.5 sec into flight, the shell attains its maximum height, y`, or 3289 m., , ⬇ 100 � 250(25.5) � 4.9(25.5) 2 ⬇ 3289, t⬇25.5
Page 33 :
1016, , Chapter 12 Vector-Valued Functions, , c. By differentiating the position function, r(t) � 25013ti � (100 � 250t � 4.9t 2)j, we obtain the velocity of the shell at any time t. Thus,, , y (m), , v(t) � r¿(t) � 25013i � (250 � 9.8t)j, , 3500, 3000, 2500, , From part (a) we know that the time of impact is t ⬇ 51.4. So at the time of, impact the velocity of the shell is, , 2000, 1500, 1000, , v(51.4) ⬇ 25013i � [250 � 9.8(51.4)] j, � 25013i � 253.7j, , 500, 0, , 5,000 10,000 15,000 20,000 x (m), , FIGURE 6, The trajectory of the shell, , 12.4, , Therefore, its speed at impact is, 冟 v(51.4) 冟 � 2(250 13)2 � (253.7)2 ⬇ 502, or 502 m/sec. The trajectory of the shell is shown in Figure 6., , CONCEPT QUESTIONS, , 1. a. What are the velocity, acceleration, and speed of an, object with position vector r(t)?, b. Give the expressions for the quantities in part (a) if the, position vector has the form r(t) � f(t)i � t(t)j � h(t)k., , 12.4, , 2. A projectile of mass m is fired from a height h with an initial velocity v0 and an angle of elevation a. Write a vector, representing, a. Its initial position., b. Its initial velocity in terms of √0 � 冟 v0 冟 and a., c. Its velocity at time t., d. Its position at time t., , EXERCISES, , In Exercises 1–6, find the velocity, acceleration, and speed of an, object with the position function for the given value of t. Sketch, the path of the object and its velocity and acceleration vectors., 1. r(t) � ti � (4 � t 2)j;, 2. r(t) � 具t 2 � 4, 2t典;, , t�1, , t�1, , 3. r(t) � cos ti � 3 sin tj;, �t, , 4. r(t) � e i � e j;, t, , 6. r(t) � 具t, t , t 典;, 2, , 3, , p, 2, , t�1, , 7. r(t) � ti � t j � (t � 4)k, 8. r(t) � 具1t, 1 � 1t, t典, 1, 9. r(t) � ti � t 2 j � k, t, , v(0) � i � 2j,, , 14. a(t) � 2i � tk,, , t�0, , 2, , 12. r(t) � t cos ti � t sin tj � t 2 k, , 13. a(t) � �32k,, , In Exercises 7–12, find the velocity, acceleration, and speed of, an object with the given position vector., 2, , 11. r(t) � et具cos t, sin t, 1典, , In Exercises 13–18, find the velocity and position vectors of an, object with the given acceleration, initial velocity, and position., , p, t�, 4, , 5. r(t) � cos ti � sin tj � tk; t �, , 10. r(t) � et i � e�t j � t 2 k, , v(0) � k,, , 15. a(t) � i � tj � (1 � t)k,, 16. a(t) � 具et, 0, e�t典,, , r(0) � 128k, , r(0) � 0, v(0) � i � k, r(0) � j � k, , v(0) � 具1, 2, 0典,, , 17. a(t) � �cos ti � sin tj � k,, , r(0) � 具3, 1, 2典, , v(0) � 2k, r(0) � i, , 18. a(t) � 具cosh t, sinh t, 0典, v(0) � 具0, 1, 1典, r(0) � 具1, 0, 0典, 19. An object moves with a constant speed. Show that the, velocity and acceleration vectors associated with this motion, are orthogonal., Hint: Study Example 5 in Section 12.2., , 20. Suppose that the acceleration of a moving object is always, 0. Show that its motion is rectilinear (that is, along a straight, line)., , V Videos for selected exercises are available online at www.academic.cengage.com/login.
Page 34 :
12.4, 21. A particle moves in three-dimensional space in such a way, that its velocity is always orthogonal to its position vector., Show that its trajectory lies on a sphere centered at the, origin., , 1017, , Velocity and Acceleration, , √0 ft/sec, determine the range of values of √0 that will allow, the man to land on the net. Neglect air resistance., y, , 22. A particle moves in three-dimensional space in such a way, that its velocity is always parallel to its position vector., Show that its trajectory lies on a straight line passing, through the origin., 23. Motion of a Projectile A projectile is fired from ground level, with an initial speed of 1500 ft/sec and an angle of elevation, of 30°., a. Find the range of the projectile., b. What is the maximum height attained by the projectile?, c. What is the speed of the projectile at impact?, 24. Motion of a Projectile Rework Exercise 23 if the projectile is, fired with an angle of elevation of 60°., , 60°, 0, , x, 150 ft, , 32. Cycloid Motion A particle of charge Q is released at rest from, the origin in a region of uniform electric and magnetic fields, described by E � Ek and B � Bi., z, , 25. Motion of a Projectile Rework Exercise 23 if the projectile, is fired with an angle of elevation of 30° from a height of, 200 ft above a level terrain., , E � Ek, , 26. Motion of a Projectile A shell is fired from a gun situated on, a hill 500 ft above level ground. If the angle of elevation, of the gun is 0° and the muzzle speed of the shell is, 2000 ft/sec, when and where will the shell strike the, ground?, 27. Motion of a Projectile A mortar shell is fired with a muzzle, speed of 500 ft/sec. Find the angle of elevation of the mortar, if the shell strikes a target located 1200 ft away., 28. Path of a Baseball A baseball player throws a ball at an angle, of 45° with the horizontal. If the ball lands 250 ft away,, what is the initial speed of the ball? (Ignore the height of, the player.), 29. An object moves in a circular path described by the position, vector, r(t) � a cos vti � a sin vtj, where v � du>dt is the constant angular velocity of the, object., a. Find the velocity vector, and show that it is orthogonal, to r(t)., b. Find the acceleration vector, and show that it always, points toward the center of the circle., c. Find the speed and the magnitude of the acceleration, vector of the object., 30. An object located at the origin is to be projected at an initial, speed of √0 m/sec and an angle of elevation of a so that it, will strike a target located at the point (r, 0). Neglecting air, resistance, find the required angle a., 31. Human Cannonball The following figure shows the trajectory, of a “human cannonball” who will be shot out of a cannon, located at ground level onto a net. If the angle of elevation, of the cannon is 60° and the initial speed of the man is, , 30 ft, , 0, y, , B � Bi, x, , a. Use the Lorentz Force Law, F � Q[E � (v B)] where, v is the velocity of the particle, to show that, F � QB, , dy, dz, j � QaE � B bk, dt, dt, , b. Use the result of part (a) and Newton’s Second Law of, Motion to show that the equations of motion of the particle take the form, d 2x, dt, , 2, , d 2y, , �0, , dt, , 2, , �v, , dz, dt, , d 2z, dt 2, , � va, , dy, E, � b, B, dt, , QB, and m is the mass of the particle., m, c. Show that the general solution of the system in part (b), is x(t) � C1t � C2, y(t) � C3 cos vt � C4 sin vt �, (E>B)t � C5, and z(t) � C4 cos vt � C3 sin vt � C6., d. Use the initial conditions, where v �, , x(0) �, , dx, (0) � 0,, dt, and, , z(0) �, , y(0) �, , dy, (0) � 0,, dt, , dz, (0) � 0, dt, , to determine C1, C2, p , C6 and hence show that the, trajectory of the particle is the cycloid x(t) � 0, y(t) �, (E>(vB))(vt � sin vt), and z(t) � (E(vB))(1 � cos vt)., (See Section 10.2.)
Page 35 :
1018, , Chapter 12 Vector-Valued Functions, , 33. Newton’s Law of Inertia As a model train moves along a, straight track at a constant speed of √0 ft/sec, a ball, bearing is ejected vertically from the train at an initial, speed of √1 ft/sec. Show that at some later time the ball, bearing will return to the location on the train from which, it was released., , 36. Motion of a Projectile Suppose that a projectile is fired from, the origin of a two-dimensional coordinate system at an, angle of elevation of a and an initial speed of √0., a. Show that the position function r(t) of the projectile is, equivalent to the parametric equations x(t) � (√0 cos a)t, and y(t) � (√0 sin a)t � (1>2)tt 2., b. Eliminate t in the equations in part (a) to find an equation in x and y describing the trajectory of the projectile., What is the shape of the trajectory?, , Note: This experiment demonstrates Newton’s Law of Inertia., , 34. Let r(t) be the position vector of a moving particle and let, r(t) � 冟 r(t) 冟., a. Show that r ⴢ r¿ � rr¿., b. What can you say about the orbit of the particle if v � r¿, is perpendicular to r?, c. What can you say about the relationship between the, velocity vector and the position vector of the particle if, the orbit is circular?, , In Exercises 37–38, determine whether the statement is true or, false. If it is true, explain why. If it is false, explain why or give, an example to show that it is false., 37. If r(t) gives the position of a particle at time t, then, r¿(t) � 冟 r¿(t) 冟T(t), where T(t) is the unit tangent vector, to the curve described by r at t and r¿(t) 0., , 35. A particle has position given by r(t) � 具t, t 2, t 3典 at time t for, 0 � t � 1. At time t � 1 the particle departs the curve and, flies off along the line tangent to the curve at r(1). If the, particle maintains a constant speed given by 冟 v(1) 冟, what is, the trajectory of the particle for t � 1? What is its position, at t � 2?, , 12.5, , 38. If a particle moves in such a way that its speed is always, constant, then its acceleration is zero., , Tangential and Normal Components of Acceleration, The Unit Normal, Suppose that C is a smooth space curve described by the vector function r(t). Then,, as we saw earlier,, , z, , N(t), , T(t) �, , C, T(t), , r(t), 0, y, x, , FIGURE 1, At each point on the curve C, the unit, normal vector N(t) is orthogonal to, T(t) and points in the direction the, curve is turning., , r¿(t), 冟 r¿(t) 冟, , r¿(t), , 0, , is the unit tangent vector to the curve C at the point corresponding to t. Since 冟 T(t) 冟 � 1, for every t, the result of Example 5 in Section 12.2 tells us that the vector T¿(t) is, orthogonal to T(t). Therefore, if r¿ is also smooth, we can normalize T¿(t) to obtain a, unit vector that is orthogonal to T(t). This vector, N(t) �, , T¿(t), 冟 T¿(t) 冟, , is called the principal unit normal vector (or simply the unit normal) to the curve, C at the point corresponding to t. (See Figure 1.), , EXAMPLE 1 Let C be the helix defined by, r(t) � 2 cos ti � 2 sin tj � tk, , t�0, , Find T(t) and N(t). Sketch C and the vectors T(p>2) and N(p>2)., Solution, , Since, r¿(t) � �2 sin ti � 2 cos tj � k, , and, 冟 r¿(t) 冟 � 24 sin2 t � 4 cos2 t � 1 � 15
Page 36 :
12.5, , Tangential and Normal Components of Acceleration, , 1019, , we have, T(t) �, , r¿(t), 1, �, (�2 sin ti � 2 cos tj � k), 冟 r¿(t) 冟, 15, , Next, differentiating T, we obtain, T¿(t) �, , 1, 2, (�2 cos ti � 2 sin tj) � �, (cos ti � sin tj), 15, 15, , Since, 2, 2, 2 cos2 t � sin2 t �, 15, 15, , 冟 T¿(t) 冟 �, it follows that, N(t) �, z, , T¿(t), � �(cos ti � sin tj), 冟 T¿(t) 冟, , In particular, at t � p>2 we have, , π, N __, 2, , (), , p, 1, 2, 1, Ta b �, (�2 sin ti � 2 cos tj � k) `, ��, i�, k, 2, 15, 15, 15, t�p>2, , π, T __, 2, , (), and, , p, Na b � �(cos ti � sin tj) `, � �j, 2, t�p>2, C, y, x, , FIGURE 2, The unit vectors T(p>2) and, N(p>2) at the point 1 0, 2, p2 2, on the helix, , The curve C and the unit vectors T(p>2) and N(p>2) are shown in Figure 2. Note, that, in general, the principal normal vector N(t) is parallel to the xy-plane and points, toward the z-axis., , Tangential and Normal Components of Acceleration, Let’s return to the study of the motion of an object moving along the curve C described, by the vector function r defined on the parameter interval I. Recall that the speed √ of, the object at any time t is √ � 冟 v(t) 冟 � 冟 r¿(t) 冟. But, T�, , r¿(t), 冟 r¿(t) 冟, , so we can write, v(t) � r¿(t) � 冟 r¿(t) 冟 T � √T, , (1), , which expresses the velocity of the object in terms of its speed and direction. (See, Figure 3.), z, √, v(t) � √T, T, r(t), , FIGURE 3, The velocity of the object, at time t is v(t) � √T., , 0, [, a, , t, , ], b, , t, , y, x
Page 37 :
1020, , Chapter 12 Vector-Valued Functions, , The acceleration of the object at time t is, a � v¿ �, , d, (√T) � √¿T � √T¿, dt, , To obtain an expression for T¿, recall that, N�, , T¿, 冟 T¿ 冟, , so T¿ � 冟 T¿ 冟 N. Now we need an expression for 冟 T¿ 冟. But from Equation (4) in Section, 12.3 we have, 冟 T¿ 冟, k�, 冟 r¿ 冟, where k is the curvature of C. This gives, 冟 T¿ 冟 � k冟 r¿ 冟 � k√, so T¿ � 冟 T¿ 冟 N � k√N., Therefore,, a � √¿T � √(k√N), , z, , a, , aN, , N, T, , aT, , 0, x, , � √¿T � k√2 N, , C, , y, , FIGURE 4, The acceleration a has a component, aTT in the tangential direction and, a component aNN in the normal, direction., , (2), , This result shows that the acceleration vector a can be resolved into the sum of two, vectors—one along the tangential direction and the other along the normal direction., The magnitude of the acceleration along the tangential direction is called the tangential scalar component of acceleration and is denoted by aT, whereas the magnitude, of the acceleration along the normal direction is called the normal scalar component, of acceleration and is denoted by aN. Thus,, a � aTT � aNN, , (3), , where, aT � √¿, , and, , aN � k√2, , (4), , (See Figure 4.), The following theorem gives formulas for calculating aT and aN directly from r and, its derivatives., , THEOREM 1 Tangential and Normal Components of Acceleration, Let r(t) be the position vector of an object moving along a smooth curve C., Then, a � aTT � aNN, where, aT �, , r¿(t) ⴢ r⬙(t), 冟 r¿(t) 冟, , and, , aN �, , 冟 r¿(t) r⬙(t) 冟, 冟 r¿(t) 冟, , PROOF If we take the dot product of v and a as given by Equations (1) and (2), we, obtain, v ⴢ a � (√T) ⴢ (√¿T � k√2 N), � √√¿T ⴢ T � k√3 T ⴢ N
Page 38 :
12.5, , Tangential and Normal Components of Acceleration, , 1021, , But T ⴢ T � 冟 T 冟2 � 1, since T is a unit vector, and T ⴢ N � 0, since T and N are orthogonal. Therefore,, v ⴢ a � √√¿, or, in view of Equation (4),, aT � √¿ �, , r¿(t) ⴢ r⬙(t), vⴢa, �, 冟 r¿(t) 冟, √, , Next, using Equation (4) and the formula for curvature (Theorem 2 in Section 12.3),, we have, aN � k√2 �, , 冟 r¿(t), , 冟 r¿(t) r⬙(t) 冟, r⬙(t) 冟, 冟 r¿(t) 冟2 �, 3, 冟 r¿(t) 冟, 冟 r¿(t) 冟, , EXAMPLE 2 A particle moves along a curve described by the vector function, r(t) � ti � t 2 j � t 3 k. Find the tangential scalar and normal scalar components of, acceleration of the particle at any time t., Solution, , We begin by computing, r¿(t) � i � 2tj � 3t 2 k, r⬙(t) � 2j � 6tk, , Then, using Theorem 1, we obtain, aT �, , r¿(t) ⴢ r⬙(t), 4t � 18t 3, �, 冟 r¿(t) 冟, 21 � 4t 2 � 9t 4, , Next, we compute, r¿(t), , i, r⬙(t) � † 1, 0, , j, 2t, 2, , k, 3t 2 † � 6t 2 i � 6tj � 2k, 6t, , Then, using Theorem 1, we have, aN �, , 冟 r¿(t) r⬙(t) 冟, 236t 4 � 36t 2 � 4, 9t 4 � 9t 2 � 1, �, 2, �, 冟 r¿(t) 冟, B 9t 4 � 4t 2 � 1, 21 � 4t 2 � 9t 4, , EXAMPLE 3 Motion of a Projectile, tion function of a shell is given by, , Refer to Example 5 in Section 12.4. The posi-, , r(t) � 250 13ti � (100 � 250t � 4.9t 2)j, a. Find the tangential and normal scalar components of acceleration of the shell at, any time t., b. Find aT(t) and aN (t) for t � 0, 12.75, 25.5, and 38.25., c. Is the shell accelerating or decelerating in the tangential direction at the values of, t specified in part (b)?, Solution, a. r¿(t) � 250 13i � (250 � 9.8t)j, r⬙(t) � �9.8j
Page 39 :
1022, , Chapter 12 Vector-Valued Functions, , The tangential scalar component acceleration of the shell is, aT (t) �, , �9.8(250 � 9.8t), r¿(t) ⴢ r⬙(t), �, 冟 r¿(t) 冟, 296.04t 2 � 4900t � 250,000, , Next, r¿(t), , i, j, r⬙(t) � † 25013 250 � 9.8t, 0, � 9.8, , k, 0 † � �245013k, 0, , So the normal scalar component of acceleration of the shell is, aN(t) �, , 冟 r¿(t) r⬙(t) 冟, 245013, �, 2, 冟 r¿(t) 冟, 296.04t � 4900t � 250,000, , b. The values of aT(t) and aN(t) for the specified values of t are shown in Table 1., TABLE 1, t, , 0, , 12.75, , aT(t), , �4.9, , �2.7, , aN(t), , 8.5, , 9.4, , 25.5, , 38.25, , 0, , 2.7, , 9.8, , 9.4, , c. Since aT(0) � �4.9 0, the shell is decelerating at t � 0. Since aT(12.75) ⬇, �2.7 0, the shell is decelerating at t � 12.75 but not by as much as it was at, t � 0. Since aT(25.5) ⬇ 0, the shell is neither accelerating nor decelerating at, t � 25.5 (when the shell is at its maximum height). Finally, since aT(38.25) ⬇, 2.7 � 0, the shell is accelerating at t � 38.25 as it continues to plunge toward, the earth., , Kepler’s Laws of Planetary Motion, We close this chapter by demonstrating how calculus can be used to derive Kepler’s, Laws of Planetary Motion. After laboring for more than 20 years analyzing the empirical data obtained by the Danish astronomer Tycho Brahe, the German astronomer, Johannes Kepler (1571–1630) formulated the following three laws describing the, motion of the planets around the sun., , Kepler’s Laws, 1. The orbit of each planet is an ellipse with the sun at one focus. (See, Figure 5a.), 2. The line joining the sun to a planet sweeps out equal areas in equal intervals of time. (See Figure 5b.), 3. The square of the period of revolution T of a planet is proportional to the, cube of the length of the major axis a of its orbit; that is, T 2 � ka 3, where, k is a constant.
Page 40 :
12.5, , Tangential and Normal Components of Acceleration, , Planet, , r(t2), , r(t3), Focus, , Focus, Sun, , A2, , A1, , 1023, , r(t1), Planet, , Sun, , r(t4), (a) The orbit of a planet is an ellipse., , (b) If the time intervals [t1, t2] and [t3, t4] are of equal, length, then the area of A1 is equal to the area of A2., , FIGURE 5, , Sir Isaac Newton proved these laws approximately 50 years after they were formulated. He showed that they were consequences of his own Law of Universal Gravitation and the Second Law of Motion. We will prove Kepler’s First Law and leave the, derivation of the other two laws as exercises. (See Exercises 37 and 38.), , Derivation of Kepler’s First Law, We begin by showing that the orbit of a planet lies in a plane. Let’s place the sun at, the origin of a coordinate system. By Newton’s Law of Gravitation the force F of gravitational attraction exerted by the sun on the planet is given by, F��, , GMm, r2, , u, , where M and m are the masses of the sun and the planet, respectively; r is the position, vector of the planet; G is the gravitational constant; r � 冟 r 冟; and u � r> 冟 r 冟 is the unit, vector having the same direction as r. This force, which is always directed toward a, fixed point O, is an example of a central force. But by Newton’s Second Law of Motion, the acceleration, a, of the planet is related to the force, F, to which it is subjected by, F � ma, Equating these two expressions for F gives, ma � �, , GMm, , u, , r2, , or, upon dividing through by m,, a��, , GM, r2, , u, , Next, we will show that for any central force, r and a satisfy r, we compute, r, , a�, , a�r, ��, , GM, r, , 2, , GM, r, , ar, , 2, , ub � �, , GM, r2, , (r, , r, GM, b � � 3 (r, 冟r冟, r, , a � 0. To see this,, , u), r) � 0, , Using this result, we have, d, (r, dt, , v) � r¿, , v�r, , v¿ � v, , v�r, , a�0�0�0
Page 41 :
1024, , Chapter 12 Vector-Valued Functions, , Integrating both sides of this equation with respect to t yields, v�c, , r, , where c is a constant vector. By the definition of the cross-product, c is orthogonal to, both r and v, and we conclude that both r(t) and v(t) lie in a fixed plane containing, the point O. This shows that the orbit of the planet is a plane curve, as was claimed, earlier. (See Figure 6.), , v, , c, , FIGURE 6, The orbit of the planet lies in, the plane passing through the, origin and orthogonal to c., , r, O, , To show that this curve is an ellipse with the sun at one focus, we observe that, c�r, , v�r, , r¿ � (ru), , (ru)¿, , � (ru), , (ru¿ � r¿u) � r 2(u, , � r (u, , u¿), , 2, , u¿) � rr¿(u, , u), , u � 0., , u, , Therefore,, a, , c � a�, , GM, r2, , [r 2(u, , ub, , u¿)] � �GM[u, , � �GM[(u ⴢ u¿)u � (u ⴢ u)u¿], , (u, , u¿)], , See Theorem 3 in Section 11.4., , 冟2, , Since u ⴢ u � 冟 u � 1, we see that u ⴢ u¿ � 0. (See Example 5 in Section 12.2.) So, the last equation reduces to, , But a, , a, , c � GMu¿, , c � v¿, , c�, , c can also be written as, a, , d, (v, dt, , Remember that c is a, constant vector., , c), , Therefore,, d, (v, dt, , c) � GMu¿ �, , d, (GMu), dt, , Integrating both sides of this equation with respect to t gives, v, , c � GMu � b, , (5), , where b is a constant vector that depends on the initial conditions. If we take the dot, product of both sides of the last equation with r, we have, r ⴢ (v, , c) � r ⴢ (GMu � b) � GMr ⴢ u � r ⴢ b, � GM(ru ⴢ u) � r ⴢ b � GMr � r ⴢ b, , But, r ⴢ (v, , c) � c ⴢ (r, , v), , � c ⴢ c � 冟c, , 冟2, , See Theorem 3 in Section 11.4.
Page 42 :
12.5, , Tangential and Normal Components of Acceleration, , 1025, , So, GMr � r ⴢ b � 冟 c 冟2 � c2, , (6), , where c � 冟 c 冟. If b � 0, then Equation (6) reduces to, GMr � c2, or, r�, , c2, GM, , and the orbit of the planet is a circle. Note that none of the orbits of the planets in our, solar system has such an orbit. So we may assume that b 0 for planets in our solar, system. In this case, letting u be the angle between r and b and writing 冟 c 冟 � c, we, can write Equation (6) in the form, GMr � 冟 r 冟冟 b 冟 cos u � c2, GMr � rb cos u � c2, or, r�, , c2, GM � b cos u, , (7), , Dividing both the numerator and denominator of Equation (7) by GM, we obtain, c2, ec2, GM, b, r�, �, b, 1 � e cos u, 1�a, b cos u, GM, where e � b>GM. Finally, if we write d � c2>b, we obtain the equation, , c, , r�, b, , ¨, , r, v, P(r, ¨), , FIGURE 7, In the plane determined by r and, c, r and u are polar coordinates., , 12.5, , ed, 1 � e cos u, , (8), , Since v c and r are both orthogonal to c, we see from Equation (5) that b is orthogonal to c. Therefore, in the plane determined by b and r (see Figure 7), we can regard, r and u as polar coordinates of a point P on the orbit of the planet. Comparing Equation (8) with that of Theorem 2 in Section 10.6, we see that it is the polar equation of, a conic section with focus at the origin and eccentricity e. Since the orbit of the planet, is a closed curve, we know that the conic must be an ellipse. This completes the proof, of Kepler’s First Law., , CONCEPT QUESTIONS, , 1. a. What are the unit tangent and the unit normal vectors at, a point on a curve? Illustrate with a sketch., b. Suppose that a curve is described by the vector function, r(t). Give formulas for computing the quantities in, part (a)., , 2. a. What are the tangential and normal components of acceleration of an acceleration vector? Illustrate with a sketch., b. Write expressions for the quantities in part (a) in terms, of r(t) and its derivatives.
Page 43 :
1026, , Chapter 12 Vector-Valued Functions, , 12.5, , EXERCISES, , In Exercises 1–4, find the unit tangent and unit normal vector, T(t) and N(t) for the curve C defined by r(t). Sketch the graph, of C, and show T(t) and N(t) for the given value of t., 1. r(t) � ti � 2t 2 j;, , t�1, , 2. r(t) � t i � 2tj;, , t�1, , 3. r(t) � t 2 i � t 3 j;, , t�1, , 2, , 4. r(t) � (2 � cos t)i � (3 � sin t)j;, , t�, , p, 4, , In Exercises 5–10, find the unit tangent and unit normal vectors, T(t) and N(t) for the curve C defined by r(t)., 6. r(t) � ti � t 2 j �, , 5. r(t) � i � tj � t 2 k, , 2 3, t k, 3, , 7. r(t) � 具sin 2t, cos 2t, 3t典, 8. r(t) � 2 cos ti � j � 2 sin tk, 9. r(t) � et具cos t, sin t, 1典, , 10. r(t) � 2ti � t 2 j � ln tk, , In Exercises 11–18, find the scalar tangential and normal components of acceleration of a particle with the given position vector., 12. r(t) � (2t 2 � 1)i � 2tj, , 11. r(t) � ti � (t 2 � 4)j, 13. r(t) � ti � t 2 j � t 3 k, 14. r(t) � t 2 i � t 3 j � t 2 k;, , t�0, , 16. r(t) � cos2 ti � sin2 tj � tk, 18. r(t) � 具t cos t, t sin t, 4典, , 19. The accompanying figure shows the path of an object moving in the plane and its acceleration vector a, its unit tangent, vector T, and its unit normal vector N at the points A and B., a. Sketch the vectors aTT and aNN at A and B., b. Is the particle accelerating or decelerating at A? At B?, y, , T, B, T, , 22. At a certain instant of time, the velocity and acceleration of, a particle at that time are v � 具2, 3, 6典 and a � 具�6, �4, 3典,, respectively., a. Find aT and aN., b. Is the particle accelerating or decelerating?, 23. The position of a particle at time t is r(t) � 具cos t 2, sin t 2典., a. Show that the path of the particle is a circular orbit with, center at the origin., b. Show that r ⴢ a � 0, where a is the acceleration vector, of the particle., Hint: Show that a ⴢ r � v ⴢ v � 0., , 24. Trajectory of a Shell A shell is fired from a howitzer with a, muzzle speed of √0 m/sec at angle of elevation of a. What, are the scalar tangential and normal components of acceleration of the shell?, 25. A particle moves along a curve C with a constant speed. Show, that the acceleration of the particle is always normal to C., 26. An object moves along a curve C with a constant speed., Show that the magnitude of the acceleration of the object is, directly proportional to the curvature of C., , 15. r(t) � 2 sin ti � 2 cos tj � tk, 17. r(t) � et具cos t, sin t, 1典, , 21. At a certain instant of time, the velocity and acceleration of, a particle are v � 2i � 3j � 6k and a � �6i � 4j � 3k,, respectively., a. Find aT and aN., b. Is the particle accelerating or decelerating?, , N, , C, , 27. Suppose that a particle moves along a plane curve that is the, graph of a function f whose second derivative exists. Show, that its normal component of acceleration is zero when the, particle is at an inflection point of the graph of f., Let C be a smooth curve defined by r(t), and let T(t) and N(t), be the unit tangent vector and unit normal vector to C corresponding to t. The plane determined by T and N is called the, osculating plane. In Exercises 28 and 29, find an equation of, the osculating plane of the curve described by r(t) at the point, corresponding to the given value of t., z, , a, , A, , Osculating plane, C, , a, N, , 0, , x, , 20. At a certain instant of time, the position, velocity, and acceleration of a particle moving in the plane are r � 4i � 2j,, v � 3i � 4j, and a � 5i � 5j, respectively., a. Sketch r, v, and a., b. Is the particle accelerating or decelerating at that instant, of time? Explain., c. Verify your assertion by computing aT., , T, , N, r, 0, , y, x, , 28. r(t) � ti � 2t 2 j � t 3 k;, , t�1, , 29. r(t) � 具et, e�t, 12t典; t � 0, , V Videos for selected exercises are available online at www.academic.cengage.com/login.
Page 44 :
12.5, Let C be a smooth curve defined by r(t), and let T(t) and N(t), be the unit tangent vector and unit normal vector to C corresponding to t. The vector B defined by B � T N is orthogonal, to T and N and is called the unit binormal vector. The vectors,, T, N, and B form a right-handed set of orthogonal unit vectors., In Exercises 30 and 31, find B for the curve described by r(t)., z, , Tangential and Normal Components of Acceleration, , 1027, , (See the figure below.), du, du, k, so r 2, � c., b. Show that c � r 2, dt, dt, dA, 1, � c, so the rate at which the area is, c. Conclude that, dt, 2, swept out is constant. This is precisely Kepler’s Second, Law., y, , N, , B, , C, , r(t), A(t), , T, r, , r(t0), x, , 0, y, x, , 30. r(t) � ti � 2t 2 j � t 3 k, 31. r(t) � 2 cosh ti � 2 sinh tj � 2tk, 32. Refer to Exercises 30 and 31. Show that B can be expressed, in terms of r and its derivatives by the formula, B�, , r¿, 冟 r¿, , r⬙, r⬙ 冟, , 33. Rework Exercise 30 using the formula for B in Exercise 32., 34. Let T, N, and B be the unit tangent, unit normal, and unit, binormal, respectively, associated with a smooth curve C, described by r(t)., a. Show that dB>ds is orthogonal to T and to B., b. Use the result of part (a) to show that dB>ds � tN for, some scalar t(t). (The number t(t) is called the torsion, of the curve. It measures the rate at which the curve, twists out of its osculating plane (the definition of an, osculating plane is given on page 1026). We define t to, be equal to 0 for a straight line.), c. Use the result of part (b) to show that the torsion of a, plane curve is zero., The torsion of a curve defined by r(t) is given by, t�, , (r¿ r⬙) ⴢ r‡, 冟 r¿ r⬙ 冟2, , In Exercises 35 and 36, find the torsion of the curve defined, by r(t)., 35. r(t) � cos ti � sin tj � tk, 36. r(t) � (t � sin t)i � (1 � cos t)j � tk, 37. Kepler’s Second Law Prove Kepler’s Second Law using the following steps. (All notation is the same as that used in the text)., a. Show that if A(t) is the area swept out by the radius, vector r(t) in the time interval [t 0, t], then, dA, 1 du, � r2, dt, 2, dt, , 38. Kepler’s Third Law Prove Kepler’s Third Law by using the following steps. In addition, suppose that the lengths of the, major and minor axes of the elliptical orbit are 2a and 2b,, respectively. (All notation is the same as that used in the, text.), a. Use the result of part (c) Exercise 37 and the fact that the, area of the ellipse is pab square units to show that, T � 2pab>c., b. Show that c2>(GM) � ed � b 2>a., c. Using the result of parts (a) and (b), show that T 2 � ka 3,, where k � 4p2>(GM)., 39. Period of the Earth’s Orbit The period of the earth’s orbit about, the sun is approximately 365.26 days. Also, the mass of the, sun is approximately 1.99 1030 kg, and the gravitational, constant is G � 6.67 10�11 Nm2/kg2. Find the length of, the major axis of the earth’s orbit., 40. Artificial Satellites A communications relay satellite is to be, placed in geosynchronous orbit; that is, its circular orbit, about the earth is to have a period of revolution of 24 hr so, that the satellite appears to be stationary in the sky. Use the, fact that the moon has a period of 27.32 days in a circular, orbit of radius 238,850 mi from the center of the earth to, determine the radius of the satellite’s orbit., 41. Motion of a Projectile A projectile is fired from a height h with, an initial speed √0 and an angle of elevation a., a. What are the scalar tangential and normal components of, acceleration of the projectile?, b. What are the scalar tangential and normal components of, acceleration of the projectile when the projectile is at its, maximum height?, 42. Trajectory of a Shell A shell is fired from a gun located on a, hill 50 m above a level terrain. The muzzle speed of the gun, is 500 m/sec, and its angle of elevation is 45°., a. Find the scalar tangential and normal components of, acceleration of the shell., Hint: Use the result of Exercise 41., , b. When is the shell accelerating, and when is it decelerating?
Page 45 :
1028, , Chapter 12 Vector-Valued Functions, , 43. Derive the following formula for calculating the, radius of curvature r of a curve C represented by, r(t) � x(t)i � y(t)j � z(t)k:, r�, , (x¿(t))2 � (y¿(t))2 � (z¿(t))2, 2(x⬙(t))2 � (y⬙(t))2 � (z⬙(t))2 � (√¿(t))2, , 44. Use the result of Exercise 43 to find the radius, of curvature of the space curve with position vector, r(t) � ti � sin tj � cos tk., , In Exercises 45–48, determine whether the statement is true or, false. If it is true, explain why it is true. If it is false, explain why, or give an example to show why it is false., 45. If 冟 r¿(t) 冟 � c, where c is a nonzero constant, then the unit normal to the curve C defined by r(t) is given by N � r⬙> 冟 r⬙ 冟., 46. If motion takes place along the x-axis, then aT � d 2x>dt 2., 47. If r(t) is the position vector of a particle with respect to, time t and r(s) is the position vector of the particle with, respect to arc length, then r⬙(t) is a scalar multiple of r⬙(s) ., 48. If r(t) is the position vector of a particle moving along a, smooth curve C, then a � √¿T � (√2>r)N, where r is the, radius of curvature., , CHAPTER, , 12, , REVIEW, , CONCEPT REVIEW, In Exercises 1–11, fill in the blanks., 1. a. A vector function is a function of the form r(t) �, , where f, t, and h are, functions, of a variable, , called a, ., b. The domain of r(t) , called the, is a, subset of the, ., 2. a. A space curve is traced out by the, point of r(t), as t takes on all values in the, interval [a, b]., b. The terminal point of r(a) corresponds to the, point of the curve, and the terminal point of r(b) gives, the, point of the curve., 3. a. If r(t) � 具 f(t), t(t), h(t)典, then lim t→a r(t) exists if and, only if, ,, , and, exist., b. A vector function r is continuous at a if lim t→a r(t) �, . The function is, on I if it is continuous at each point in I., 4. a. The derivative of r is r¿(t) �, , provided that the, limit exists., b. If r(t) � 具 f(t), t(t), h(t)典, then r¿(t) �, ., 5. a. If u and v are differentiable, then, , d, [u(t) ⴢ v(t)] �, dt, , d, , and [u(t) v(t)] �, ., dt, b. If u is differentiable and f is differentiable, then, d, ., [u( f(t))] �, dt, 6. If f, t, and h are integrable and r(t) � 具 f(t), t(t), h(t)典, then, a. 兰 r(t) dt �, ., b. 兰ab r(t) dt �, ., 7. The length of the curve C, r(t) � 具 f(t), t(t), h(t)典, where, ., a � t � b, is given by L �, , 8. a. A curve C described by r(t) with parameter t is said to, be, by t., b. The arc length function s associated with a smooth curve, ., C described by r(t) is s(t) �, c. The curve C has arc length parametrization if it is parametrized by the, function s(t)., 9. a. If a smooth curve C is described by r(s), where s is the, arc length parameter, then the curvature of C is k(s) �, ., b. If C is parametrized by t, then k(t) �, ., c. The curvature of C is also given by k(t) �, ., d. If C is a plane curve, then k(x) �, ., e. For a plane curve C, the reciprocal of the curvature at, the point P is called the, of C at P, and the circle with this, that shares, a common, with the curve at P is, called the, ., 10. If the position vector of a particle is r(t), then its velocity, is, , its speed is, , and its acceleration, is, . The acceleration vector points toward the, side of the trajectory of the particle., 11. a. If C is a smooth curve described by the vector function, ,, r(t), then the unit tangent vector is T(t) �, and the principal unit normal vector is N(t) �, ., b. The acceleration of a particle can be resolved into the, sum of two vectors—one along the direction of, and the other along the direction of, ., In fact, a � aTT � aNN, where aT �, and, ; the former is called the scalar, aN �, component of acceleration, and the latter is called the, scalar, component of acceleration., c. In terms of r and its derivatives, aT �, , and, ., aN �
Page 46 :
1034, , Chapter 13 Functions of Several Variables, , 13.1, , Functions of Two or More Variables, Functions of Two Variables, Up to now, we have dealt only with functions of one variable. In practice, however, we, often encounter situations in which one quantity depends on two or more quantities., For example, consider the following:, The volume V of a right circular cylinder depends on its radius r and its height, h (V � pr 2h)., The volume V of a rectangular box depends on its length l, width w, and height, h (V � lwh)., The revenue R from the sale of commodities A, B, C, and D at the unit prices of, 10, 14, 20, and 30 dollars, respectively, depends on the number of units x, y, z,, and w of commodities A, B, C, and D sold (R � 10x � 14y � 20z � 30w)., Just as we used a function of one variable to describe the dependency of one variable on another, we can use the notion of a function of several variables to describe, the dependency of one variable on several variables. We begin with the definition of a, function of two variables., , DEFINITION Function of Two Variables, Let D � {(x, y) 冟 x, y 僆 R} be a subset of the xy-plane. A function f of two variables is a rule that assigns to each ordered pair of real numbers (x, y) in D a, unique real number z. The set D is called the domain of f, and the set of corresponding values of z is called the range of f., , The number z is usually written z � f(x, y) . The variables x and y are independent, variables, and z is the dependent variable., As in the case of a function of a single variable, a function of two or more variables can be described verbally, numerically, graphically, or algebraically., , EXAMPLE 1 Home Mortgage Payments In a typical housing loan, the borrower, makes periodic payments toward reducing indebtedness to the lender, who charges, interest at a fixed rate on the unpaid portion of the debt. In practice, the borrower is, required to repay the lender in periodic installments, usually of the same size over a, fixed term, so that the loan (principal plus interest charges) is amortized at the end, of the term. Table 1 gives the monthly loan repayment on a loan of $1000, f(t, r),, where t is the term of the loan in years and r is the interest rate per annum (%/year), compounded monthly. Referring to the table, we see that the monthly installment, for a 30-year loan of $1000 when the current interest rate is 7%/year is given by, f(30, 7) � 6.6530 (dollars). Therefore, if the amount borrowed is $350,000, the monthly, repayment is 350(6.6530), or $2328.55.
Page 47 :
13.1, , 1035, , Functions of Two or More Variables, , TABLE 1, Interest rate %/year, , Term of the loan (years), , t, , r, , 6, , 6 14, , 6 12, , 6 34, , 7, , 7 14, , 7 12, , 7 34, , 8, , 5, , 19.3328, , 19.4493, , 19.5661, , 19.6835, , 19.8012, , 19.9194, , 20.0379, , 20.1570, , 20.2764, , 10, , 11.1021, , 11.2280, , 11.3548, , 11.4824, , 11.6108, , 11.7401, , 11.8702, , 12.0011, , 12.1328, , 15, , 8.4386, , 8.5742, , 8.7111, , 8.8491, , 8.9883, , 9.1286, , 9.2701, , 9.4128, , 9.5565, , 20, , 7.1643, , 7.3093, , 7.4557, , 7.6036, , 7.7530, , 7.9038, , 8.0559, , 8.2095, , 8.3644, , 25, , 6.4430, , 6.5967, , 6.7521, , 6.9091, , 7.0678, , 7.2281, , 7.3899, , 7.5533, , 7.7182, , 30, , 5.9955, , 6.1572, , 6.3207, , 6.4860, , 6.6530, , 6.8218, , 6.9921, , 7.1641, , 7.3376, , 35, , 5.7019, , 5.8708, , 6.0415, , 6.2142, , 6.3886, , 6.5647, , 6.7424, , 6.9218, , 7.1026, , 40, , 5.5021, , 5.6774, , 5.8546, , 6.0336, , 6.2143, , 6.3967, , 6.5807, , 6.7662, , 6.9531, , Although the monthly installments based on a $1000 loan are displayed in the form, of a table for selected values of t and r in Example 1, an algebraic expression for computing f(t, r) also exists:, f(t, r) �, , 10r, 12c1 � a1 �, , 0.01r �12t, b, d, 12, , But as in the case of a single variable, we are primarily interested in functions that can, be described by an equation relating the dependent variable z to the independent, variables x and y. Also, as in the case of a single variable, unless otherwise specified,, the domain of a function of two variables is the set of all points (x, y) for which, z � f(x, y) is a real number., , EXAMPLE 2 Let f(x, y) � x 2 � xy � 2y. Find the domain of f, and evaluate f(1, 2),, , f(2, 1), f(t, 2t), f(x 2, y) , and f(x � y, x � y)., , Solution Since x 2 � xy � 2y is a real number whenever (x, y) is an ordered pair of, real numbers, we see that the domain of f is the entire xy-plane. Next, we have, f(1, 2) � 12 � (1)(2) � 2(2) � 3, f(2, 1) � 22 � (2)(1) � 2(1) � 4, f(t, 2t) � t 2 � (t)(2t) � 2(2t) � �t 2 � 4t, f(x 2, y) � (x 2)2 � (x 2)(y) � 2y � x 4 � x 2y � 2y, and, f(x � y, x � y) � (x � y)2 � (x � y)(x � y) � 2(x � y), � x 2 � 2xy � y 2 � x 2 � y 2 � 2x � 2y, � 2(y 2 � xy � x � y)
Page 48 :
1036, , Chapter 13 Functions of Several Variables, y, , EXAMPLE 3 Find and sketch the domain of the function:, Test point (1, 0), , 1, 0, �1, , x, , 1 2 3, , x � y2, , a. f(x, y) � 2y 2 � x, , b. t(x, y) �, , ln(x � y � 1), y�x, , Solution, a. f(x, y) is a real number provided that y 2 � x � 0. Therefore, the domain of f is, D � {(x, y) 冟 y 2 � x � 0}, , (a) The domain of f(x, y) � √ y 2 � x, y, y�x, 1, , Test point (1, 0), 0, , �1, , x, , 1, , x � y � 1 � 0 �1, , (b) The domain of g(x, y) �, , ln(x � y � 1), y�x, , To sketch the region D, we first draw the curve y 2 � x � 0, or y 2 � x, which, is a parabola (Figure 1a). Observe that this curve divides the xy-plane into two, regions: the points satisfying y 2 � x � 0 and the points satisfying y 2 � x � 0., To determine the region of interest, we pick a point in one of the regions, say,, the point (1, 0). Substituting the coordinates x � 1 and y � 0 into the inequality, y 2 � x � 0, we obtain 0 � 1 � 0, which is false. This shows that the test point, is not contained in the required region. Therefore, the region that does not contain, the test point together with the curve x � y 2 is the required domain (Figure 1a)., b. Because the logarithmic function is defined only for positive numbers, we must, have x � y � 1 � 0. Furthermore, the denominator of the expression cannot be, zero, so y � x � 0, or y � x. Therefore, the domain of t is, D � {(x, y) 冟 x � y � 1 � 0 and, , FIGURE 1, , y � x}, , To sketch the domain of D, we first draw the graph of the equation, x�y�1�0, which is a straight line. The dashed line is used to indicate that points on the line, are not included in D. This line divides the xy-plane into two half-planes. If we, pick the test point (1, 0) and substitute the coordinates x � 1 and y � 0 into, the inequality x � y � 1 � 0, we obtain 2 � 0, which is true. This computation, tells us that the upper half-plane containing the test point satisfies the inequality, x � y � 1 � 0. Next, because y � x, all the points lying on the line y � x in this, half-plane must be excluded from D. Again, we indicate this with a dashed line, (Figure 1b)., , z, , (x, y, z), , z � f (x, y), , Graphs of Functions of Two Variables, Just as the graph of a function of one variable enables us to visualize the function, so, too does the graph of a function of two variables., , S, , 0, , DEFINITION Graph of a Function of Two Variables, y, x, , (x, y), , D, , FIGURE 2, The graph of f is the surface, S consisting of all points (x, y, z),, where z � f(x, y) and (x, y) 僆 D., , Let f be a function of two variables with domain D. The graph of f is the set, S � {(x, y, z) 冟 z � f(x, y), (x, y) 僆 D}, , Since each ordered triple (x, y, z) may be represented as a point in threedimensional space, R3, the set S is a surface in space (see Figure 2).
Page 49 :
13.1, , Functions of Two or More Variables, , 1037, , EXAMPLE 4 Sketch the graph of f(x, y) � 29 � x 2 � y 2. What is the range of f ?, Solution The domain of f is D � {(x, y) 冟 x 2 � y 2, tered at the origin. Writing z � f(x, y), we have, , 9}, the disk with radius 3, cen-, , z � 29 � x 2 � y 2, z2 � 9 � x 2 � y2, or, x 2 � y2 � z2 � 9, The last equation represents a sphere of radius 3 centered at the origin. Since z � 0,, we see that the graph of f is just an upper hemisphere (Figure 3). Furthermore, z must, be less than or equal to 3, so the range of f is [0, 3]., z, (0, 0, 3), , 0, V, , FIGURE 3, The graph of f(x, y) � 29 � x 2 � y 2, is the upper hemisphere of radius 3,, centered at the origin., , (0, 3, 0), , (3, 0, 0), , y, , x, , Computer Graphics, The graph of a function of two variables can be sketched with the aid of a graphing, utility. In most cases the techniques that are used involve plotting the traces of a surface in the vertical planes x � k and y � k for equally spaced values of k. The program uses a “hidden line” routine that determines what parts of certain traces should, be eliminated to give the illusion of the surface in three dimensions. In the next example we sketch the graph of a function of two variables and then show a computergenerated version of it., , EXAMPLE 5 Let f(x, y) � x 2 � 4y 2., a. Sketch the graph of f., , b. Use a CAS to plot the graph of f., , Solution, a. We recognize that the graph of the function is the surface z � x 2 � 4y 2, which is, the elliptic paraboloid, x2, �, 1, , y2, 1 2, a b, 2, , �z, , Using the drawing skills developed in Section 11.6, we obtain the sketch shown, in Figure 4a.
Page 50 :
1038, , Chapter 13 Functions of Several Variables, , b. The computer-generated graph of f is shown in Figure 4(b)., z, z, , 4, 1, , 1, , 2, , 2, , 1, , 1, , 2, V, FIGURE 4, The graph of f(x, y) � x 2 � 4y 2, , 2, , y, , y, , x, , x, , (a), , (b), , Figure 5 shows the computer-generated graphs of several functions., z, , z, , y, , x, , y, , x, , cos (x 2 � 2y 2), (b) f (x, y) � ___________, 1 � x 2 � 2y 2, , (a) f (x, y) � x 3 � 3y 2x, z, , z, , y, , FIGURE 5, Some computer-generated, graphs of functions of, two variables, , x, , y, x, 2, , (c) f (x, y) � x 2y 2e �x � y, , 2, , (d) f (x, y) � ln ( x 2 � 2y 2 � 1)
Page 51 :
13.1, , Functions of Two or More Variables, , 1039, , Level Curves, We can visualize the graph of a function of two variables by using level curves. To, define the level curve of a function f of two variables, let z � f(x, y) and consider the, trace of f in the plane z � k (k, a constant), as shown in Figure 6a. If we project this, trace onto the xy-plane, we obtain a curve C with equation f(x, y) � k, called a level, curve of f (Figure 6b)., y, , z, z � f (x, y), , f (x, y) � k, C, , z�k, 0, f (x, y) � k, , x, , y, 0, , C, , FIGURE 6, , (a) The level curve C with equation f(x, y) � k, is the projection of the trace of f in the, plane z � k onto the xy-plane., , x, , (b) The level curve C, , DEFINITION Level Curves, The level curves of a function f of two variables are the curves in the xy-plane, with equations f(x, y) � k, where k is a constant in the range of f., Notice that the level curve with equation f(x, y) � k is the set of all points in the, domain of f corresponding to the points on the surface z � f(x, y) having the same, height or depth k. By drawing the level curves corresponding to several admissible values of k, we obtain a contour map. The map enables us to visualize the surface represented by the graph of z � f(x, y): We simply lift or depress the level curve to see the, “cross sections” of the surface. Figure 7a shows a hill, and Figure 7b shows a contour, map associated with that hill., y, , z, , 800, 600, 400, 200, 0, , 400, , 600, , 200, 0, , y, x, , FIGURE 7, , (a) A hill, , 0, (b) A contour map of the hill, , x
Page 52 :
1040, , Chapter 13 Functions of Several Variables, , EXAMPLE 6 Sketch a contour map for the surface described by f(x, y) � x 2 � y 2,, , using the level curves corresponding to k � 0, 1, 4, 9, and 16., , Solution The level curve of f corresponding to each value of k is a circle x 2 � y 2 � k, of radius 1k, centered at the origin. For example, if k � 4, the level curve is the circle with equation x 2 � y 2 � 4, centered at the origin and having radius 2. The required, contour map of f comprises the origin and the four concentric circles shown in Figure 8a., The graph of f is the paraboloid shown in Figure 8b., z, , y, , z � x 2 � y2, , k�0, k�1, k�4, k�9, k � 16, x, , 0, y, x, V, , (a) Contour map for f (x, y) � x 2 � y2, , FIGURE 8, , (b) The graph of z � x 2 � y2, , EXAMPLE 7 Sketch a contour map for the hyperbolic paraboloid defined by, f(x, y) � y 2 � x 2., Solution The level curve corresponding to each value of k is the graph of the equation y 2 � x 2 � k. For k � 0 the level curves have equations, y2, x2, �, �1, k, k, or, y2, ( 1k)2, , �, , x2, ( 1k)2, , �1, , These curves are a family of hyperbolas with asymptotes y � x and vertices, (0, 1k). For example, if k � 4, then the level curve is the hyperbola, y2, x2, �, �1, 4, 4, with vertices (0, 2)., If k � 0, the level curves have equations y 2 � x 2 � k or x 2 � y 2 � �k, which can, be put in the standard form, x2, ( 1�k)2, , �, , y2, ( 1�k)2, , �1, , and represent a family of hyperbolas with asymptotes y � x. The contour map comprising the level curves corresponding to k � 0, 2, 4, 6, and 8 is sketched in, Figure 9a. The graph of z � y 2 � x 2 is shown in Figure 9b.
Page 53 :
13.1, , y, , Functions of Two or More Variables, , 1041, , z, , k�0, , 0, x, y, x, , k�0, V, , FIGURE 9, , (a) Contour map for f (x, y) � y2 � x 2, , (b) The graph of z � y2 � x 2, , Figure 10 shows some computer-generated graphs of functions of two variables and, their corresponding level curves., , z, , z, , z, , x, y, y, y, , x, x, x 2 � 2y 2, (a) Graph of f (x, y) � cos ________, 4, , (, , ), , 2, , (c) Graph of f (x, y) � �xye �x � y, , (b) Graph of f (x, y) � y 4 � 8y 2 � 4x 2, , y, , y, , y, , x, , x 2 � 2y 2, (d) Level curves of f (x, y) � cos ________, 4, , (, , ), , FIGURE 10, The graphs of some functions and their level curves, , 2, , x, , x, , (e) Level curves of f (x, y) � y 4 � 8y 2 � 4x 2, , 2, , (f) Level curves of f (x, y) � �xye �x � y, , 2
Page 54 :
1042, , Chapter 13 Functions of Several Variables, , Aside from their use in constructing topographic maps of mountain ranges, level, curves are found in many areas of practical interest. For example, if T(x, y) denotes the, temperature at a location within the continental United States with longitude x and latitude y at a certain time of day, then the temperature at the point (x, y) is the height, (or depth) of the surface with equation z � T(x, y). In this context the level curve, T(x, y) � k is a curve superimposed on the map of the United States connecting all, points that have the same temperature at a given time (Figure 11). These level curves, are called isotherms. Similarly, if P(x, y) measures the barometric pressure at the location (x, y), then the level curves of the function P are called isobars. All points on an, isobar P(x, y) � k have the same barometric pressure at a given time., 50, , 40, , 30, 30, , 60, , 40, 70, , 50, 60, , 80, , 70, 80, , FIGURE 11, Isotherms: level curves connecting, points that have the same temperature, , 70, , 80, , 80, , Functions of Three Variables and Level Surfaces, A function f of three variables is a rule that assigns to each ordered triple (x, y, z) in a, domain D � {(x, y, z) 冟 x, y, z 僆 R} a unique real number w denoted by f(x, y, z). For, example, the volume V of a rectangular box of length x, width y, and height z can be, described by the function f defined by f(x, y, z) � xyz., , EXAMPLE 8 Find the domain of the function f defined by, f(x, y, z) � 1x � y � z � xeyz, Solution f(x, y, z) is a real number provided that x � y � z � 0 or, equivalently,, z x � y. Therefore, the domain of f is, D � {(x, y, z) 冟 z, , x � y}, , This is the half-space consisting of all points lying on or below the plane z � x � y., , Since the graph of a function of three variables is composed of the points, (x, y, z, w), where w � f(x, y, z), lying in four-dimensional space, we cannot draw the, graphs of such functions. But by examining the level surfaces, which are the surfaces, with equations, f(x, y, z) � k, , k, a constant, , we are often able to gain some insight into the nature of f.
Page 55 :
13.1, , Functions of Two or More Variables, , 1043, , EXAMPLE 9 Find the level surfaces of the function f defined by, , z, , f(x, y, z) � x 2 � y 2 � z 2, , k�1, k�4, k�9, , Solution The required level surfaces of f are the graphs of the equations, x 2 � y 2 � z 2 � k, where k � 0. These surfaces are concentric spheres of radius 1k, centered at the origin (see Figure 12). Observe that f has the same value for all points, (x, y, z) lying on any such sphere., y, , x, , FIGURE 12, The level surfaces of, f(x, y, z) � x 2 � y 2 � z 2, corresponding to k � 1, 4, 9, , 13.1, , CONCEPT QUESTIONS, 4. What is a level surface of a function of three variables? If, w � T(x, y, z) gives the temperature of a point (x, y, z) in, three-dimensional space, what does the level surface w � k, describe?, , 1. What is a function of two variables? Give an example of, one by stating its rule, domain, and range., 2. What is the graph of a function of two variables? Illustrate, with a sketch., 3. What is a level curve of a function of two variables? Illustrate with a sketch., , 13.1, , EXERCISES, , 1. Let f(x, y) � x 2 � 3xy � 2x � 3. Find, a. f(1, 2), b. f(2, 1), c. f(2h, 3k), d. f(x � h, y), e. f(x, y � k), 2. Let t(x, y) �, , 2xy, 2x � 3y 2, 2, , 9. t(x, y) � 24 � x 2 � y 2, 2, , x, y�z, , 12. t(x, y, z) �, , . Find, , a. t(�1, 2), c. t(u, �√), e. t(u � √, √), , 10. h(x, y) � ln(xy � 1), , 11. f(x, y, z) � 29 � x � y � z 2, 2, , 13. h(u, √, w) � tan u � √ cos w, , b. t(2, �1), d. t(2, a), , 1, , 14. f(x, y, z) �, , 24 � x � y 2 � z 2, 2, , 3. Let f(x, y, z) � 2x 2 � 2y 2 � 3z 2. Find, a. f(1, 2, 3), b. f(0, 2, �1), c. f(t, �t, t), d. f(u, u � 1, u � 1), e. f(�x, x, �2x), , In Exercises 15–22, find and sketch the domain of the function., , 4. Let t(r, s, t) � res>t. Find, a. t(2, 0, 3), c. t(�1, �1, �1), e. t(r � h, s � k, t � l), , 17. f(u, √) �, b. t(1, ln 3, 1), d. t(t, t, t), , 15. f(x, y) � 1y � 1x, , 7. f(u, √) �, , u√, u�√, , u � √2, , 20. h(x, y) �, , ln(y � x), 1x � y � 1, , 6. t(x, y) � x � 2y � 3, , 21. f(x, y, z) � 29 � x 2 � y 2 � z 2, , 8. h(x, y) � 1x � 2y, , 22. t(x, y, z) �, , 2, , 2, , V Videos for selected exercises are available online at www.academic.cengage.com/login., , 24 � x 2 � y 2, z�3, , xy, 2x � y, , 18. h(x, y) � 1xy � 1, , 19. f(x, y) � x ln y � y ln x, , In Exercises 5–14, find the domain and the range of the function., 5. f(x, y) � x � 3y � 1, , u√, 2, , 16. t(x, y) �
Page 56 :
1044, , Chapter 13 Functions of Several Variables, , In Exercises 23–30, sketch the graph of the function., 23. f(x, y) � 4, , In Exercises 33–38, match the function with one of the graphs, labeled a through f., (a), , 24. f(x, y) � 6 � 2x � 3y, , (b), z, , 25. f(x, y) � x 2 � y 2, , z, , 26. t(x, y) � y 2, 27. h(x, y) � 9 � x 2 � y 2, 28. f(x, y) � 2x 2 � y 2, 29. f(x, y) �, , 1, 236 � 9x 2 � 36y 2, 2, , y, , y, x, , 30. f(x, y) � cos x, , x, , 31. The figure shows the contour map of a hill. The numbers in, the figure are measured in feet. Use the figure to answer the, questions below., , (d), , (c), , z, , z, , N, W, , E, , C, , S, 500, , 400, , S, , y, , 300, 200, , B, , x, y, , 100, x, , A, (e), , (f), z, , z, , a. What is the altitude of the point on the hill corresponding to the point A? The point B?, b. If you start out from the point on the hill corresponding, to point A and move north, will you be ascending or, descending? What if you move east from the point on the, hill corresponding to point B?, c. Is the hill steeper at the point corresponding to A or at, the point corresponding to C? Explain., 32. A contour map of a function f is shown in the figure. Use it, to estimate the value of f at P and Q., y, , 4, , Q, 3, , 23.5, 18.4, 12.5, 8.0, , 35. f(x, y) � cos, , x, cos y, 2, , 2�y2, , 36. f(x, y) � (x 2 � y 2)e�x, , 0, , 38. f(x, y) � �, , graph of the function., x, , 39. f(x, y) � 3x 2 � 3y 2 � 2, 2�y2, , 40. f(x, y) � (4x 2 � 9y 2)e�x, , P, , �2, , 34. f(x, y) � cos(x 2 � y 2), , 33. f(x, y) � 2x 2 � y 3, , 41. f(x, y) � cos x � cos y, , �19.9, , 42. f(x, y) �, 2, , x, 2(x 2 � y 2), , cas In Exercises 39–42, use a computer or calculator to plot the, , �3.8, �3.6, �9.3, �14.5, �26.7, , y, , x, , 2�y2, , 0, , �4, �4, , x, , 37. f(x) � e�x, , 2, , �2, , y, , 4, , 1 � 2 sin(x 2 � y 2), x 2 � y2
Page 57 :
13.1, In Exercises 43–52, sketch the level curves f(x, y) � k of the, function for the indicated values of k., , 1045, , Functions of Two or More Variables, , (e), , (f), y, , y, , 43. f(x, y) � 2x � 3y; k � �2, �1, 0, 1, 2, 44. f(x, y) � x 2 � 4y 2; k � 0, 1, 2, 3, 4, 45. f(x, y) � xy; k � �2, �1, 0, 1, 2, 46. f(x, y) � 216 � x 2 � y 2;, , k � 0, 1, 2, 3, 4, , 48. f(x, y) � y 2 � x 2;, , k � �2, �1, 0, 1, 2, , 49. f(x, y) � ln(x � y);, , k � �2, �1, 0, 1, 2, , 2�4y2, , 57. f(x, y) � e1�2x, , x, 50. f(x, y) � ; k � �2, �1, 0, 1, 2, y, 51. f(x, y) � y � x 2;, 52. f(x, y) � x � sin y;, , x, , x, , x�y, 47. f(x, y) �, ; k � �2, 0, 1, 2, x�y, , z, , k � �2, �1, 0, 1, 2, k � �2, �1, 0, 1, 2, , In Exercises 53–56, describe the level surfaces of the function., 53. f(x, y, z) � 2x � 4y � 3z � 1, 54. f(x, y, z) � 2x 2 � 3y 2 � 6z 2, 55. f(x, y, z) � x 2 � y 2 � z 2, 56. f(x, y, z) � �x 2 � y 2 � z � 2, y, , In Exercises 57–62, match the graph of the surface with one of, the contour maps labeled a through f., , x, , 58. f(x, y) � x � y, , (b), , (a), y, , 2, , z, , y, , x, , (c), , x, , (d), , y, y, , y, , x, , 59. f(x, y) � cos2x � y, 2, , x, , 2, , z, , x, y, , x
Page 58 :
1046, , Chapter 13 Functions of Several Variables, , 60. f(x, y) � sin x � sin y, , 68. Find an equation of the level surface of f(x, y, z) � 2x 2 �, 3y 2 � z that contains the point (�1, 2, �3)., , z, , 69. Can two level curves of a function f of two variables x and y, intersect? Explain., 70. A level set of f is the set S � {(x, y) 冟 f(x, y) � k, where k is, in the range of f}. Let, y, , f(x, y) � e, , 0, x 2 � y2 � 1, , if x 2 � y 2 � 1, if x 2 � y 2 � 1, , Sketch the level set of f for k � 0 and 3., 71. Refer to Exercise 70. Let, , x, , 61. f(x, y) � sin(x � y), , f(x, y) � e, , z, , 1 � 2x 2 � y 2, x 2 � y2 � 1, , if x 2 � y 2 � 1, if x 2 � y 2 � 1, , (a) Sketch the graph of f and (b) describe the level set of f, for k � 0, 12, 1, and 3., 72. Body Mass The body mass index (BMI) is used to identify,, evaluate, and treat overweight and obese adults. The BMI, value for an adult of weight w (in kilograms) and height h, (in meters) is defined to be, M � f(w, h) �, , y, x, , 62. f(x, y) � ln(2x 2 � y 2), , z, , w, h2, , According to federal guidelines, an adult is overweight if he, or she has a BMI value between 25 and 29.9 and is “obese”, if the value is greater than or equal to 30., a. What is the BMI of an adult who weighs in at 80 kg and, stands 1.8 m tall?, b. What is the maximum weight of an adult of height 1.8 m, who is not classified as overweight or obese?, 73. Poiseuille’s Law Poiseuille’s Law states that the resistance R,, measured in dynes, of blood flowing in a blood vessel of, length l and radius r (both in centimeters) is given by, R � f(l, r) �, , y, , x, cas In Exercises 63–66, (a) use a computer or calculator to plot the, , graph of the function f, and (b) plot some level curves of f and, compare them with the graph obtained in part (a)., 63. f(x, y) � 冟 x 冟 � 冟 y 冟, 65. f(x, y) �, , 64. f(x, y) �, , xy, 2x � y, 2, , 2, , xy(x 2 � y 2), x 2 � y2, 2�y2, , 66. f(x, y) � ye1�x, , 67. Find an equation of the level curve of f(x, y) � 2x 2 � y 2, that contains the point (3, 4)., , kl, r4, , where k is the viscosity of blood (in dyne-sec/cm2). What is, the resistance, in terms of k, of blood flowing through an, arteriole with radius 0.1 cm and length 4 cm?, 74. Surface Area of a Human Body An empirical formula by, E.F. Dubois relates the surface area S of a human body (in, square meters) to its weight W (in kilograms) and its height, h (in centimeters). The formula, given by, S � 0.007184W 0.425H 0.725, is used by physiologists in metabolism studies., a. Find the domain of the function S., b. What is the surface area of a human body that weighs, 70 kg and has a height of 178 cm?, 75. Cobb-Douglas Production Function Economists have found that, the output of a finished product, f(x, y), is sometimes, described by the function, f(x, y) � ax by 1�b
Page 59 :
13.1, where x stands for the amount of money expended for labor,, y stands for the amount expended on capital, and a and b, are positive constants with 0 � b � 1., a. If p is a positive number, show that f( px, py) � pf(x, y)., b. Use the result of part (a) to show that if the amount of, money expended for labor and capital are both increased, by r percent, then the output is also increased by r percent., 76. Continuous Compound Interest If a principal of P dollars is, deposited in an account earning interest at the rate of r/year, compounded continuously, then the accumulated amount at, the end of t years is given by, A � f(P, r, t) � Pert, dollars. Find the accumulated amount at the end of 3 years, if $10,000 is deposited in an account earning interest at the, rate of 10%/year., 77. Home Mortgages Suppose a home buyer secures a bank loan, of A dollars to purchase a house. If the interest rate charged, is r/year and the loan is to be amortized in t years, then the, principal repayment at the end of i months is given by, B � f(A, r, t, i) � A c, , 1 1 � 12r 2 i � 1, d, 1 1 � 12r 2 12t � 1, , 0, , i, , 12t, , Suppose the Blakelys borrow $280,000 from a bank to, help finance the purchase of a house and the bank charges, interest at a rate of 6%/year, compounded monthly. If the, Blakelys agree to repay the loan in equal installments over, 30 years, how much will they owe the bank after the sixtieth, payment (5 years)? The 240th payment (20 years)?, 78. Wilson Lot-Size Formula The Wilson lot-size formula in economics states that the optimal quantity Q of goods for a, store to order is given by, Q � f(C, N, h) �, , 2CN, B h, , where C is the cost of placing an order, N is the number of, items the store sells per week, and h is the weekly holding, cost for each item. Find the most economical quantity of, ten-speed bicycles to order if it costs the store $20 to place, an order and $5 to hold a bicycle for a week and the store, expects to sell 40 bicycles a week., 79. Force Generated by a Centrifuge A centrifuge is a machine, designed for the specific purpose of subjecting materials to a, sustained centrifugal force. The magnitude of a centrifugal, force F in dynes is given by, F � f(M, S, R) �, , p2S 2MR, 900, , where S is in revolutions per minute (rpm), M is the mass in, grams, and R is the radius in centimeters. Find the centrifugal force generated by an object revolving at the rate of, 600 rpm in a circle of radius 10 cm. Express your answer, as a multiple of the force of gravity. (Recall that 1 gram of, force is equal to 980 dynes.), , Functions of Two or More Variables, , 1047, , 80. Temperature of a Thin Metal Plate A thin metal plate located in, the xy-plane has a temperature of, T(x, y) �, , 120, 1 � 2x 2 � y 2, , degrees Celsius at the point (x, y). Describe the isotherms, of T, and sketch those corresponding to T � 120, 60, 40,, and 20., 81. International America’s Cup Class Drafted by an international, committee in 1989, the rules for the new International, America’s cup class includes a formula that governs the, basic yacht dimensions. The formula f(L, S, D) 42,, where, f(L, S, D) �, , L � 1.25S 1>2 � 9.80D 1>3, 0.388, , balances the rated length L (in meters), the rated sail area S, (in square meters) and the displacement D (in cubic meters)., All changes in the basic dimensions are tradeoffs. For, example, if you want to pick up speed by increasing the, sail area, you must pay for it by decreasing the length or, increasing the displacement, both of which slow the boat, down. Show that yacht A of rated length 20.95 m, rated sail, area 277.3 m2, and displacement 17.56 m3, and the longer, and heavier yacht B with L � 21.87, S � 311.78, and, D � 22.48 both satisfy the formula., 82. Ideal Gas Law According to the ideal gas law, the volume V, of an ideal gas is related to its pressure P and temperature T, by the formula, V�, , kT, P, , where k is a positive constant. Describe the level curves of, V, and give a physical interpretation of your result., 83. Newton’s Law of Gravitation According to Newton’s Law of, Gravitation a body of mass m 1 located at the origin of an, xyz-coordinate system attracts another body of mass m 2, located at the point (x, y, z) with a force of magnitude, given by, F�, , Gm 1m 2, x � y2 � z2, 2, , where G is the universal constant of gravitation. Describe, the level surfaces of F, and give a physical interpretation of, your result., 84. Equipotential Curves Consider the crescent-shaped region R (in, the following figure) that lies inside the disk, D1 � {(x, y) 冟 (x � 2)2 � y 2, , 4}, , and outside the disk, D2 � {(x, y) 冟 (x � 1)2 � y 2, , 1}
Page 60 :
1048, , Chapter 13 Functions of Several Variables, y, , where c is the speed of sound in still air, about 1100 ft/sec., (This phenomenon is called the Doppler effect.) Suppose, a railroad train is traveling at 100 ft/sec (approximately, 68 mph) in still air and the frequency of a note emitted by, the locomotive whistle is 500 Hz. What is the frequency of, the note heard by a passenger in a train moving at 50 ft/sec, in the opposite direction to the first train?, , 2, D1, ƒ � 50, , 1, , ƒ � 100, , R, , D2, 0, , 1, , 2, , 3, , x, , 4, , 86. A function f(x, y) is homogeneous of degree n if it satisfies, the equation f(tx, ty) � t nf(x, y) for all t. Show that, , �1, �2, , xy � y 2, 2x � y, , f(x, y) �, , If the electrostatic potential along the inner circle is kept at, 50 volts and the electrostatic potential along the outer circle, is kept at 100 volts, then the electrostatic potential at any, point (x, y) in the region R is given by, f(x, y) � 150 �, , 200x, x 2 � y2, , Show that the equipotential curves of f are arcs of circles, that have their centers on the positive x-axis and pass, through the origin. Sketch the equipotential curve corresponding to a potential of 75 volts., 85. The Doppler Effect Suppose that a sound with frequency f is, emitted by an object moving along a straight line with speed, u and that a listener is traveling along the same line in the, opposite direction with speed √. Then the frequency F heard, by the listener is given by, F�a, , is homogeneous of degree 1., In Exercises 87–90, determine whether the statement is true or, false. If it is true, explain why it is true. If it is false, give an, example to show why it is false., 87. f is a function of x and y if and only if for any two, points P1(x 1, y1) and P2 (x 2, y2) in the domain of f,, f(x 1, y1) � f(x 2, y2) implies that P1 (x 1, y1) � P2(x 2, y2)., 88. The equation x 2 � y 2 � z 2 � 4 defines at least two functions of x and y., 89. The level curves of a function f of two variables, f(x, y) � k,, exist for all values of k., 90. The level surfaces of the function f(x, y, z) � ax � by �, cz � d consist of a family of parallel planes that are orthogonal to the vector n � ai � bj � ck., , c�√, bf, c�u, , 13.2 Limits and Continuity, An Intuitive Definition of a Limit, Figure 1 shows the graph of a function f of two variables. This figure suggests that, f(x, y) is close to the number L if the point (x, y) is close to the point (a, b)., z, f (x, y), L, (x, y, f (x, y)), , z � f (x, y), , FIGURE 1, The functional value f(x, y) is close, to L if (x, y) is close to (a, b)., , 0, x, , (a, b), , (x, y), , y
Page 61 :
13.2, , Limits and Continuity, , 1049, , DEFINITION Limit of a Function of Two Variables at a Point, Let f be a function that is defined for all points (x, y) close to the point (a, b), with the possible exception of (a, b) itself. Then the limit of f(x, y) as (x, y), approaches (a, b) is L, written, lim, , (x, y)→(a, b), , f(x, y) � L, , if f(x, y) can be made as close to L as we please by restricting (x, y) to be sufficiently close to (a, b)., , y, , (a, b), , 0, , FIGURE 2, There are infinitely many paths the, point (x, y) could take in approaching, the point (a, b)., , x, , At first glance, there appears to be little difference between this definition and the, definition of the limit of a function of one variable, with the exception that the points, (x, y) and (a, b) lie in the plane. But there are subtle differences. In the case of a function of one variable, the point x can approach the point x � a from only two directions: from the left and from the right. As a consequence, the function f has a limit L, as x approaches a if and only if f(x) approaches L from the left (lim x→a� f(x) � L) and, from the right (lim x→a� f(x) � L), a fact that we observed in Section 1.1., The situation is a little more complicated in the case of a function of two variables, because there are infinitely many ways in which we can approach a point (a, b) in the, plane (Figure 2). Thus, if f has a limit L as (x, y) approaches (a, b) , then f(x, y) must, approach L along every possible path leading to (a, b)., To see why this is true, suppose that, f(x, y) → L 1, , as, , (x, y) → (a, b), , f(x, y) → L 2, , as, , (x, y) → (a, b), , along a path C1 and that, along another path C2, where L 1 � L 2. Then no matter how close (x, y) is to (a, b),, f(x, y) will assume values that are close to L 1 and also values that are close to L 2 depending on whether (x, y) is on C1 or on C2. Therefore, f(x, y) cannot be made as close as, we please to a unique number L by restricting (x, y) to be sufficiently close to (a, b);, that is, lim (x, y)→(a, b) f(x, y) cannot exist., An immediate consequence of this observation is the following criterion for demonstrating that a limit does not exist., , Technique for Showing That lim (x, y)→(a, b) f(x, y) Does Not Exist, If f(x, y) approaches two different numbers as (x, y) approaches (a, b) along two, different paths, then lim (x, y)→(a, b) f(x, y) � L does not exist., , EXAMPLE 1 Show that, , lim, , (x, y)→(0, 0), , x 2 � y2, x 2 � y2, , does not exist., , Solution The function f(x, y) � (x 2 � y 2)>(x 2 � y 2) is defined everywhere except at, (0, 0). Let’s approach (0, 0) along the x-axis (see Figure 3). On the path C1, y � 0, so, lim, (x, y)→(0, 0), along C1, , f(x, y) � lim f(x, 0) � lim, x→0, , x→0, , x2, x2, , � lim 1 � 1, x→0
Page 62 :
1050, , Chapter 13 Functions of Several Variables, , Next, let’s approach (0, 0) along the y-axis. On the path C2, x � 0 (Figure 3), so, , y, , lim, (0, y), , (x, y)→(0, 0), along C2, , C2, , y→0, , FIGURE 3, A point on C1 has the form (x, 0), and, a point on C2 has the form (0, y)., , EXAMPLE 2 Show that, , � lim (�1) � �1, y→0, , xy, , lim, , (x, y)→(0, 0), , x � y2, 2, , does not exist., , Solution The function f(x, y) � xy>(x 2 � y 2) is defined everywhere except at (0, 0)., Let’s approach (0, 0) along the x-axis (Figure 4). On the path C1, y � 0, so, lim, (x, y)→(0, 0), along C1, , y, , f(x, y) � lim f(x, 0) � lim, x→0, , x→0, , (x, x), C2, C3, , lim, , C1, (x, 0), , 0, x2, , � lim 0 � 0, x→0, , Similarly, you can show that f(x, y) also approaches 0 as (x, y) approaches (0, 0) along, the y-axis, path C2 (Figure 4)., Now consider yet another approach to (0, 0), this time along the line y � x (Figure 4). On the path C3, y = x, so, , y�x, , 0, , y2, , x, , (x, 0), , (0, y), , y→0, , �y 2, , Since f(x, y) approaches two different numbers as (x, y) approaches (0, 0) along two, different paths, we conclude that the given limit does not exist., , C1, 0, , f(x, y) � lim f(0, y) � lim, , x, , FIGURE 4, f(x, y) → 0 as (x, y) → (0, 0) along, C1 and C2, but f(x, y) → 12 as, (x, y) → (0, 0) along C3, so, lim (x, y)→(0, 0) f(x, y) does not exist., , (x, y)→(0, 0), along C3, , f(x, y) � lim f(x, x) � lim, x→0, , x→0, , x2, x2 � x2, , � lim, , x→0, , 1, 1, �, 2, 2, , Since f(x, y) approaches two different numbers as (x, y) approaches (0, 0) along two, different paths, we conclude that the given limit does not exist., The graph of f shown in Figure 5 confirms this result visually. Notice the ridge that, occurs above the line y � x because f(x, y) � 12 for all points (x, y) on that line except, at the origin., z, y, , x, , FIGURE 5, xy, The graph of f(x, y) � 2, x � y2, , Although the method of Examples 1 and 2 is effective in demonstrating when a, limit does not exist, it cannot be used to prove the existence of the limit of a function, at a point. Using this method, we would have to show that f(x, y) approaches a unique, number L as (x, y) approaches the point along every path, which is clearly an impossible task. Fortunately, the Limit Laws for a function of a single variable can be extended, to functions of two or more variables. For example, the Sum Law, the Product Law,, the Quotient Law, and so forth, all hold. So does the Squeeze Theorem.
Page 63 :
13.2, , Limits and Continuity, , 1051, , EXAMPLE 3 Evaluate, a. lim (x, y)→(1, 2) (x 3y 2 � x 2y � x 2 � 2x � 3y), b. lim (x, y)→(2, 4), , 8xy, B 2x � y, 3, , Solution, a. We have, lim, , (x, y)→(1, 2), , (x 3y 2 � x 2y � x 2 � 2x � 3y) � (1)3(2)2 � (1)2(2) � (1)2 � 2(1) � 3(2), �7, , b. We have, 8xy, 8xy, � 3, lim, (x, y)→(2, 4) B 2x � y, B (x, y)→(2, 4) 2x � y, 3, , lim, , �, , 8(2)(4), 3, �1, 8�2, B 2(2) � 4, 3, , The next example utilizes the Squeeze Theorem to show the existence of a limit., , EXAMPLE 4 Find, , 2x 2y, , lim, , x 2 � y2, , (x, y)→(0, 0), , if it exists., , Solution Observe that the numerator of the rational function has degree 3, whereas, the denominator has degree 2. This suggests that when x and y are both close to zero,, the numerator is much smaller than the denominator, and we suspect that the limit, might exist and that it is equal to zero., To prove our assertion, we observe that y 2 � 0, so x 2>(x 2 � y 2) 1. Therefore,, `, , 0, Let f(x, y) � 0, t(x, y) � `, lim, , (x, y)→(0, 0), , f(x, y) �, , 2x 2y, x2 � y, , 2x 2y, x 2 � y2, , lim, , (x, y)→(0, 0), , `�, 2, , 2x 2 冟 y 冟, , 2冟y冟, , x 2 � y2, , ` , and h(x, y) � 2 冟 y 冟. Then, , 0�0, , and, , lim, , (x, y)→(0, 0), , h(x, y) �, , lim, , (x, y)→(0, 0), , 2冟y冟 � 0, , By the Squeeze Theorem,, lim, , (x, y)→(0, 0), , t(x, y) �, , lim, , (x, y)→(0, 0), , `, , 2x 2y, x 2 � y2, , `�0, , and this, in turn, implies that, lim, , (x, y)→(0, 0), , 2x 2y, x 2 � y2, , �0, , Continuity of a Function of Two Variables, The definition of continuity for a function of two variables is similar to that for a function of one variable.
Page 64 :
1052, , Chapter 13 Functions of Several Variables, , DEFINITION Continuity at a Point, Let f be a function that is defined for all points (x, y) close to the point (a, b)., Then f is continuous at the point (a, b) if, lim, , (x, y)→(a, b), , f(x, y) � f(a, b), , Thus, f is continuous at (a, b) if f(x, y) approaches f(a, b) as (x, y) approaches (a, b), along any path. Loosely speaking, a function f is continuous at a point (a, b) if the graph, of f does not have a hole, gap, or jump at (a, b). If f is not continuous at (a, b), then f, is said to be discontinuous there. For example, the functions f, t, and h whose graphs, are shown in Figure 6 are discontinuous at the indicated points., z, , z, , z, (c, d, g(c, d)), , 0, , FIGURE 6, , 0, , 0, y, , (a, b), , x, , z � h(x, y), , z � g(x, y), , z � f (x, y), , (c, d), , x, , (a) f is not defined at (a, b)., , (b), , lim, , (x, y) → (c, d), , g(x, y) � g(c, d), , y, , y, x, (c), , lim, , (x, y) → (0, 0), , h(x, y) does not exist., , y, , Continuity on a Set, , ∂, (a, b), , N∂, , Let’s digress a little to introduce some terminology. We define the D-neighborhood, about (a, b) to be the set, Nd � {(x, y) 冟 2(x � a)2 � (y � b)2 � d}, x, , 0, , FIGURE 7, The d-neighborhood about (a, b), y, Interior, point, Boundary, point, , Thus, Nd is just the set of all points lying inside the circle of radius d centered at (a, b), (see Figure 7)., Let R be a plane region. A point (a, b) is said to be an interior point of R if there, exists a d-neighborhood about (a, b) that lies entirely in R (Figure 8). A point (a, b) is, called a boundary point of R if every d-neighborhood of R contains points in R and, also points not in R., A region R is said to be an open region if every point of R is an interior point of, R. A region is closed if it contains all of its boundary points. Finally, a region that contains some but not all of its boundary points is neither open nor closed. For example,, the regions, , R, 0, , x, , FIGURE 8, An interior point and a boundary point of R, , A � e(x, y) `, , y2, x2, �, � 1f ,, 9, 4, , B � e(x, y) `, , y2, x2, �, 9, 4, , 1f, , and, C � e(x, y) `, , y2, x2, �, 9, 4, , y2, x2, 1; y � 0f d e(x, y) `, �, � 1; y � 0f, 9, 4
Page 65 :
13.2, , C, , B, , A, x, , x, , 0, , 0, , x, , (c) C is neither open nor closed., , (b) B is closed., , (a) A is open., , 1053, , y, , y, , y, , 0, , Limits and Continuity, , FIGURE 9, Every point in A is an interior point; B contains all of its boundary points;, C contains some but not all of its boundary points., , shown in Figure 9a–c are open, closed, and neither open nor closed, respectively., As we mentioned in Section 1.3, continuity is a “local” concept. The following definition explains what we mean by continuity on a region., , DEFINITION Continuity on a Region, Let R be a region in the plane. Then f is continuous on R if f is continuous at, every point (x, y) in R. If (a, b) is a boundary point, the condition for continuity is modified to read, lim, , (x, y)→(a, b), , f(x, y) � f(a, b), , where (x, y) 僆 R, that is, (x, y) is restricted to approach (a, b) along paths lying, inside R., , EXAMPLE 5 Show that the function f defined by f(x, y) � 29 � x 2 � y 2 is contin-, , uous on the closed region R � {(x, y) 冟 x 2 � y 2 9}, which is the set of all points lying, on and inside the circle of radius 3 centered at (0, 0) in the xy-plane., Solution Observe that the set R is precisely the domain of f. Now, if (a, b) is any interior point of R, then, lim, , (x, y)→(a, b), , f(x, y) �, , lim, , (x, y)→(a, b), , �2, , lim, , 29 � x 2 � y 2, , (x, y)→(a, b), , (9 � x 2 � y 2), , � 29 � a 2 � b 2, � f(a, b), This shows that f is continuous at (a, b)., Next, if (c, d) is a boundary point of R and (x, y) is restricted to lie inside R, we, obtain, lim, , (x, y)→(c, d), , f(x, y) � f(c, d), , as before, thus showing that f is continuous at (c, d) as well., The graph of f is the upper hemisphere of radius 3 centered at the origin together, with the circle in the xy-plane having equation x 2 � y 2 � 9. (See Figure 10.)
Page 66 :
1054, , Chapter 13 Functions of Several Variables, , z, 3, , z � f (x, y), , 0, , 3, , 3, , FIGURE 10, The graph of f(x, y) � 29 � x 2 � y 2, has no holes, gaps, or jumps., , y, , x, , The following theorem summarizes the properties of continuous functions of, two variables. The proofs of these properties follow from the limit laws and will be, omitted., , THEOREM 1 Properties of Continuous Functions of Two Variables, If f and t are continuous at (a, b) , then the following functions are also continuous at (a, b)., a. f, , b. ft, , t, , c. cf, , c, a constant, , d. f>t t(a, b) � 0, , A consequence of Theorem 1 is that polynomial and rational functions are continuous., A polynomial function of two variables is a function whose rule can be expressed, as a finite sum of terms of the form cx my n, where c is a constant and m and n are nonnegative integers. For example, the function f defined by, f(x, y) � 2x 2y 5 � 3xy 3 � 8xy 2 � 3y � 4, is a polynomial function in the two variables x and y. A rational function is the quotient of two polynomial functions. For example, the function t defined by, t(x, y) �, , x 3 � xy � y 2, x 2 � y2, , is a rational function., , THEOREM 2 Continuity of Polynomial and Rational Functions, A polynomial function is continuous everywhere (that is, in the whole plane)., A rational function is continuous at all points in its domain (that is, at all points, where its denominator is defined and not equal to zero)., , EXAMPLE 6 Determine where the function is continuous:, a. f(x, y) �, , xy(x 2 � y 2), x �y, 2, , 2, , b. t(x, y) �, , 1, y � x2
Page 67 :
13.2, , Limits and Continuity, , 1055, , Solution, a. The function f is a rational function and is therefore continuous everywhere, except at (0, 0) , where its denominator is equal to zero (Figure 11)., b. The function t is a rational function and is continuous everywhere except along, the curve y � x 2, where its denominator is equal to zero (Figure 12)., z, , y, , x, , 0, , y, , x, , FIGURE 11, The graph of f has a hole at the origin., , xy (x 2 � y 2_), (b) The graph of z � _________, x2 � y2, , (a) The domain of f, , z, y, , y � x2, y, , FIGURE 12, As (x, y) approaches the curve y � x 2, from the region y � x 2, z � f(x, y), approaches infinity; as (x, y), approaches the curve y � x 2 from, the region y � x 2, z approaches, minus infinity., , x, , 0, , x, 1, (b) The graph of z � _______2, y�x, , (a) The domain of t, , The next theorem tells us that the composite function of two continuous functions, is also a continuous function., , THEOREM 3 Continuity of a Composite Function, If f is continuous at (a, b) and t is continuous at f(a, b), then the composite function h � t ⴰ f defined by h(x, y) � t( f(x, y)) is continuous at (a, b)., , EXAMPLE 7 Determine where the function is continuous:, a. F(x, y) � sin xy, , b. G(x, y) �, , 1, 2, , cos(2x 2 � y 2), 1 � 2x 2 � y 2
Page 68 :
1056, , Chapter 13 Functions of Several Variables, , Solution, a. We can view the function F as the composition t ⴰ f of the functions f and t, defined by f(x, y) � xy and t(t) � sin t. Thus,, F(x, y) � t( f(x, y)) � sin ( f(x, y)) � sin xy, Since f is continuous on the whole plane and t is continuous on (�⬁, ⬁), we conclude that F is continuous everywhere. The graph of F is shown in Figure 13a., b. The function G is the quotient of p(x, y) � 12 cos(2x 2 � y 2) and q(x, y) �, 1 � 2x 2 � y 2. The function p in turn involves the composition of t(t) � 12 cos t, and f(x, y) � 2x 2 � y 2. Since both f and t are continuous everywhere, we, see that p is continuous everywhere. The function q is continuous everywhere, as well and is never zero. Therefore, by Theorem 3, G is continuous everywhere., The graph of G is shown in Figure 13b., z, , z, , y, y, x, , x, , FIGURE 13, , cos (2x 2 � y 2), (b) G(x, y) � ____________, is continuous everywhere., 1 � 2x 2 � y 2, 1_, 2, , (a) F(x, y) � sin xy is continuous everywhere., , Functions of Three or More Variables, The notions of the limit of a function of three or more variables and that of the continuity of a function of three or more variables parallel those of a function of two variables. For example, if f is a function of three variables, then we write, lim, , (x, y, z)→(a, b, c), , f(x, y, z) � L, , to mean that there exists a number L such that f(x, y, z) can be made as close to L as, we please by restricting (x, y, z) to be sufficiently close to (a, b, c)., , EXAMPLE 8 Evaluate, , limp, , e2y(sin x � cos y), , (x, y, z)→( 2 , 0, 1), , 1 � y2 � z2, , Solution, limp, , (x, y, z)→( 2 , 0, 1), , e2y(sin x � cos y), 1�y �z, 2, , 2, , �, , ., , e0[sin (p>2) � cos 0], 1�0�1, , A function f of three variables is continuous at (a, b, c) if, lim, , (x, y, z)→(a, b, c), , f(x, y, z) � f(a, b, c), , �, , 2, �1, 2
Page 69 :
13.2, , Limits and Continuity, , 1057, , ln z, , EXAMPLE 9 Determine where f(x, y, z) �, , is continuous., 21 � x 2 � y 2 � z 2, Solution We require that z � 0 and 1 � x 2 � y 2 � z 2 � 0; that is, z � 0 and, x 2 � y 2 � z 2 � 1. So f is continuous on the set {(x, y, z) 冟 x 2 � y 2 � z 2 � 1 and, z � 0}, which is the set of points above the xy-plane and inside the upper hemisphere, with center at the origin and radius 1., , The E-D Definition of a Limit (Optional), The notion of the limit of a function of two variables given earlier can be made more, precise as follows., , DEFINITION Limit of f(x, y), Let f be a function of two variables that is defined for all points (x, y) on a disk, with center at (a, b) with the possible exception of (a, b) itself. Then, lim, , (x, y)→(a, b), , f(x, y) � L, , if for every e � 0, there exists a d � 0 such that, 冟 f(x, y) � L 冟 � e, , Geometrically speaking, f has the limit L at (a, b) if given any e � 0, we can find, a circle of radius d centered at (a, b) such that L � e � f(x, y) � L � e for all interior points (x, y) � (a, b) of the circle (Figure 14)., , z, L+´, f(x, y), , L, (x, y, f(x, y)), , L−´, , EXAMPLE 10 Prove that lim (x, y)→(a, b) x � a., Solution, , Let e � 0 be given. We need to show that there exists a d � 0 such that, , z � f(x, y), 0, y, x, , 0 � 2(x � a)2 � (y � b)2 � d, , whenever, , ∂, (a, b), , FIGURE 14, f(x, y) lies in the interval, (L � e, L � e) whenever, (x, y) � (a, b) is in the, d-neighborhood of (a, b)., , 冟 f(x, y) � a 冟 � e, whenever (x, y) � (a, b) is in the d-neighborhood about (a, b). To find such a d, consider, 冟 f(x, y) � a 冟 � 冟 x � a 冟 � 2(x � a)2, , (x, y), , 2(x � a)2 � (y � b)2, , Thus, if we pick d � e, we see that d � 0 and that 2(x � a)2 � (y � b)2 � d implies, that 冟 f(x, y) � a 冟 � e as was to be shown. Since e is arbitrary, the proof is complete., , EXAMPLE 11 Prove that, Solution, , lim, , (x, y)→(0, 0), , 2x 2y, x 2 � y2, , � 0. (See Example 4.), , Let e � 0 be given. Consider, 冟 f(x, y) � 0 冟 � `, , 2x 2y, x2 � y, , ` � 2 冟 y 冟a, 2, , 2 冟 y 冟 � 22y 2, , x2, x 2 � y2, , b, , (x, y) � (0, 0), , 22x 2 � y 2, , If we pick d � e>2, then d � 0, and 2x 2 � y 2 � d implies that 冟 f(x, y) � 0 冟 � e., Since e is arbitrary, the proof is complete.
Page 70 :
1058, , Chapter 13 Functions of Several Variables, , 13.2, , CONCEPT QUESTIONS, , 1. a. Explain what it means for a function f of two variables to, have a limit at (a, b)., b. Describe a technique that you could use to show that the, limit of f(x, y) as (x, y) approaches (a, b) does not exist., 2. Explain what it means for a function of two variables to be, continuous (a) at a point (a, b) and (b) on a region in the, plane., 3. Determine whether each function f is continuous or discontinuous. Explain your answer., a. f(P, T ) measures the volume of a balloon ascending into, the sky as a function of the atmospheric pressure P and, the air temperature T., , 13.2, , EXERCISES, , In Exercises 1–12, show that the limit does not exist., x �y, 2, , 1., , lim, , (x, y)→(0, 0), , 3., , lim, , (x, y)→(0, 0), , 5., , lim, , (x, y)→(0, 0), , 7., , lim, , (x, y)→(1, 0), , 8., , lim, , (x, y)→(0, 0), , 9., , 3x � y, 2, , 17., , 2x � 3xy � 4y, 2, , (x, y)→(0, 0), , 2xy, 2x � y, , lim, , 4., , lim, , 6., , 4, , (x, y)→(0, 0), , 2, , x �y, 2, , 23., 25., , x �y �z, , 2, , 22., , lim, , lim, , e�x sin�1(y � x), , lim, , e2x, , (x, y)→(0, 1), , ln(x 2 � 3y), , lim, , 24., , x 2 sin p(2x � y), x, sin�1 a b, y, x, 1�, y, , (x, y)→(0, 1), , cos�1(x � 2y), , lim, , x � 2y 2 � z 4, 2, , x � t 2, y � t 2, z � t., , 27., , lim, , (x, y)→(0, 0), , 29., , lim, , (x, y)→(0, 0), , xy, , lim, , lim, , (x, y)→11, 12 2, , 2, , �y2, , (x, y)→(3, 4), , xy � yz � xz, xyz � 3, [esin px � ln(cos p(y � z))], , In Exercises 27–30, use polar coordinates to find the limit. Hint:, If x � r cos u and y � r sin u, then (x, y) → (0, 0) if and only if, r → 0�., , x � y3 � z3, 3, , Hint: Approach (0, 0, 0) along the curve with parametric equations, , (x, y, z)→(0, 0, 0), , lim, , 20., , x, tan�1 a b, y, , (x, y, z)→(0, 3, 1), , xz 2 � 2y 2, , lim, , e, x�y�1, , (x, y, z)→(1, 2, 3), , 26., , 2xyz, , lim, , lim, , (x, y)→(2, 1), , xy � yz � xz, , (x, y, z)→(0, 0, 0), , 12., , 21., , (x, y)→(1, 1), , 2x 2 � y 6, , 18., , 2x � y 2, , sin xy, x 2 � y2, , xy 3 cos x, , 2, , lim, , (x, y)→(0�, 0�), , 4, , x 2 � y 2 � 2x � 1, , 2, , (x, y)→(1, �2), , 2, , 1x�y, , 19., , xy 2, , 2xy � 2y, , lim, , 3xy, , lim, , 2x 2 � 3y 2, , (x, y)→(0, 0), , 2, , 4, , lim, , 2., , 3xy, , (x, y, z)→(0, 0, 0), , 11., , 2, , 2x 2 � y 2, , (x, y, z)→(0, 0, 0), , 10., , b. f(H, W) measures the surface area of a human body as a, function of its height H and weight W., c. f(d, t) measures the fare as a function of distance d and, time t for taking a cab from O’Hare Airport to downtown, Chicago., d. f(T, P) measures the volume of a certain mass of gas as a, function of the temperature T and the pressure P., 4. Suppose f has the property that it is not defined at the point, (1, 2) but lim (x, y)→(1, 2) f(x, y) � 3. Can you define f(1, 2) so, that f is continuous at (1, 2)? If so, what should the value of, f(1, 2) be?, , x 2 � y2 � z2, , 30., , lim, , (x, y)→(0, 0), , x 3 � y3, , 28., , x 2 � y2, , lim, , (x, y)→(0, 0), , sin(2x 2 � 2y 2), x 2 � y2, , (x � y ) ln(x � y ), 2, , 2, , 2, , 2, , tan(2x 2 � 2y 2), tanh(3x 2 � 3y 2), , In Exercises 13–26, find the given limit., 13., , lim, , (x, y)→(1, 2), , 14., 15., , lim, , (x 2 � 2y 2), , (x, y)→(1, �1), , lim, , (x, y)→(1, 2), , In Exercises 31–40, determine where the function is continuous., 31. f(x, y) �, , (2x � xy � 3y � 1), 2, , 2x 2 � 3y 3 � 4, 3 � xy, , 16., , lim, , (x, y)→(�1, 3), , x � 2y 2, (x � 1)(y � 1), , 2xy, 2x � 3y � 1, , 32. f(x, y) �, , x 3 � xy � y 3, x 2 � y2, , 33. t(x, y) � 1x � y � 1x � y, 34. h(x, y) � sin(2x � 3y), , V Videos for selected exercises are available online at www.academic.cengage.com/login., , 35. F(x, y) � 1xex>y
Page 71 :
13.3, , 2, , 48. f(x, y) � y ln x, t(t) � et, , xyz, x 2 � y2 � z2 � 4, , 49. Use the precise definition of a limit to prove that, lim (x, y)→(a, b) c � c where c is a constant., , 38. t(x, y, z) � 1x � cos 1y � z, 39. h(x, y, z) � x ln(yz � 1), 40. F(x, y, z) � x tan, , 1059, , 47. f(x, y) � x tan y, t(t) � cos t, , 36. G(x, y) � ln(2x � y), 37. f(x, y, z) �, , Partial Derivatives, , 50. Use the precise definition of a limit to prove that, lim (x, y)→(a, b) y � b., , y, z, , 51. Use the precise definition of a limit to prove that, , 41. Let, sin xy, f(x, y) � • xy, 1, , lim, , if xy � 0, if xy � 0, , a. Determine all the points where f is continuous., , (x, y)→(0, 0), , 3xy 3, x 2 � y2, , �0, , 52. Use the precise definition of a limit to prove that if, lim (x, y)→(a, b) f(x, y) � L and c is a constant, then, lim (x, y)→(a, b) cf(x, y) � cL., , cas b. Plot the graph of f. Does the graph give a visual confir-, , In Exercises 53–58, determine whether the statement is true or, false. If it is true, explain why it is true. If it is false, give an, example to show why it is false., , mation of your conclusion in part (a)?, 42. Let, x, �y, f(x, y) � • sin x, 1�y, , if x � 0, if x � 0, , a. Determine all the points where f is continuous., cas b. Plot the graph of f. Does the graph give a visual confir-, , mation of your conclusion in part (a)?, In Exercises 43–48, find h(x, y) � t( f(x, y)), and determine, where h is continuous., 43. f(x, y) � x � xy � y , t(t) � t cos t � sin t, 2, , 2, , 44. f(x, y) � x � xy � xy � y , t(t) � te, 3, , 2, , 45. f(x, y) � 2x � y, t(t) �, , 3, , 54. If lim (x, y)→(a, b) f(x, y) � L and f is defined at (a, b) , then, f(a, b) � L., 55. If f(x, y) � t(x)h(y) , where t and h are continuous at a and, b, respectively, then f is continuous at (a, b) ., 56. If f(1, 3) � 4, then lim (x, y)→(1, 3) f(x, y) � 4., 57. If f is continuous at (3, �1) and f(3, �1) � 2, then, lim (x, y)→(3, �1) f(x, y) � 2., 58. If f is continuous at (a, b) and t is continuous at f(a, b) ,, then lim (x, y)→(a, b) t( f(x, y)) � t( f(a, b)) ., , t�2, t�1, , 46. f(x, y) � x � 2y � 3, t(t) � 1t �, , �t, , 53. If lim (x, y)→(a, b) f(x, y) � L, then, lim (x, y)→(a, b) along C f(x, y) � L, where C is any path leading, to (a, b) ., , 1, t, , 13.3 Partial Derivatives, Partial Derivatives of Functions of Two Variables, For a function of one variable x, there is no ambiguity when we speak of the rate of, change of f(x) with respect to x. The situation becomes more complicated, however,, when we study the rate of change of a function of two or more variables. For example, for the function of two variables defined by the equation z � f(x, y), both the independent variables x and y may be allowed to vary in some arbitrary fashion, thus making it unclear what we mean by the phrase “the rate of change of z with respect to x, and y.”, One way of getting around this difficulty is to hold one variable constant and consider the rate of change of f with respect to the other variable. This approach might be, familiar to anyone who has used the expression “everything else being equal” while, debating the merits of a complicated issue.
Page 72 :
1060, , Chapter 13 Functions of Several Variables, , Specifically, suppose that (a, b) is a point in the domain of f. Fix y � b. Then the, function that is defined by z � f(x, b) is a function of the single variable x. Its graph, is the curve C formed by the intersection of the vertical plane y � b and the surface, z � f(x, y) (Figure 1)., Therefore, the quantity, , z, T, C, (a, b, f (a, b)), z � f (x, y), , f(a � h, b) � f(a, b), h→0, h, lim, , 0, y�b, , y, (a, b), , x, , FIGURE 1, f(a � h, b) � f(a, b), lim, measures, h→0, h, the slope of T and the rate of change, of f(x, y) in the x-direction when, x � a and y � b., z, , (a, b, f(a, b)), , if it exists, measures both the slope of the tangent line T to the curve C at the point, (a, b, f(a, b)) as well as the rate of change of f(x, y) with respect to x (in the xdirection) with y held constant when x � a and y � b., Similarly, the quantity, f(a, b � h) � f(a, b), h→0, h, lim, , x�a, , T, , 0, , x, , DEFINITIONS Partial Derivatives of a Function of Two Variables, Let z � f(x, y). Then the partial derivative of f with respect to x is, , y, (a, b), , FIGURE 2, f(a, b � h) � f(a, b), lim, measures, h→0, h, the slope of T and the rate of change, of f(x, y) in the y-direction when, x � a and y � b., , (2), , if it exists, measures the slope of the tangent line T to the curve C (formed by the intersection of the vertical plane x � a and the surface z � f(x, y) at (a, b, f(a, b)), and the, rate of change of f(x, y) with respect to y (in the y-direction) with x held constant when, x � a and y � b (Figure 2)., In expressions (1) and (2) the point (a, b) is fixed but otherwise arbitrary. Therefore, we may replace (a, b) by (x, y), leading to the following definitions., , z � f (x, y), C, , (1), , f, f(x � h, y) � f(x, y), � lim, x h→0, h, and the partial derivative of f with respect to y is, f, f(x, y � h) � f(x, y), � lim, y h→0, h, provided that each limit exists., , Computing Partial Derivatives, The partial derivatives of f can be calculated by using the following rules., , Computing Partial Derivatives, To compute f> x, treat y as a constant and differentiate in the usual manner, with respect to x (an operation that we denote by > x)., To compute f> y, treat x as a constant and differentiate in the usual manner with respect to y (an operation that we denote by > y).
Page 73 :
13.3, , Partial Derivatives, , 1061, , f, f, and, if f(x, y) � 2x 2y 3 � 3xy 2 � 2x 2 � 3y 2 � 1., x, y, , EXAMPLE 1 Find, , Solution To compute f> x, we think of the variable y as a constant and differentiate with respect to x. Let’s write, f(x, y) � 2x 2y 3 � 3xy 2 � 2x 2 � 3y 2 � 1, where the variable y to be treated as a constant is shown in color. Then, f, � 4xy 3 � 3y 2 � 4x, x, To compute f> y, we think of the variable x as a constant and differentiate with, respect to y. In this case,, f(x, y) � 2x 2y 3 � 3xy 2 � 2x 2 � 3y 2 � 1, and, f, � 6x 2y 2 � 6xy � 6y, y, Before looking at more examples, let’s introduce some alternative notations for the, partial derivatives of a function. If z � f(x, y), then, x, , f(x, y) �, , f, � fx � z x, x, , and, , y, , f(x, y) �, , f, � fy � z y, y, , EXAMPLE 2 Find fx and fy if f(x, y) � x cos xy 2., Solution To compute fx, we think of the variable y as a constant and differentiate with, respect to x. Thus,, f(x, y) � x cos xy 2, and, fx �, , x, , (x cos xy 2) � x, , � x(�sin xy 2), , x, , x, , (cos xy 2) � (cos xy 2), , (xy 2) � cos xy 2, , x, , (x), , Use the Product Rule., , Use the Chain Rule on the first term., , � �xy 2 sin xy 2 � cos xy 2, Next, to compute fy, we treat x as a constant and differentiate with respect to y., Thus,, f(x, y) � x cos xy 2, and, fy �, , y, , (x cos xy 2) � x, , � x(�sin xy 2), , y, , y, , (cos xy 2) � (cos xy 2), , (xy 2) � 0 � �2x 2y sin xy 2, , y, , (x)
Page 74 :
1062, , Chapter 13 Functions of Several Variables, , EXAMPLE 3 Let f(x, y) � 4 � 2x 2 � y 2. Find the slope of the tangent line at the, , point (1, 1, 1) on the curve formed by the intersection of the surface z � f(x, y) and, a. the plane y � 1, , b. the plane x � 1, , Solution, a. The slope of the tangent line at any point on the curve formed by the intersection, of the plane y � 1 and the surface z � 4 � 2x 2 � y 2 is given by, f, �, (4 � 2x 2 � y 2) � �4x, x, x, In particular, the slope of the required tangent line is, f, `, � �4(1) � �4, x (1, 1), b. The slope of the tangent line at any point on the curve formed by the intersection, of the plane x � 1 and the surface z � 4 � 2x 2 � y 2 is given by, f, �, (4 � 2x 2 � y 2) � �2y, y, y, In particular, the slope of the required tangent line is, f, `, � �2(1) � �2, y (1, 1), (See Figure 3.), z, , z, T, T, C, x�1, , y�1, , C, (1, 1, 1), , (1, 1, 1), , 0, , 0, y, , y, , x, , x, , (a) The slope of the tangent line is −4., , FIGURE 3, , (b) The slope of the tangent line is −2., , EXAMPLE 4 Electrostatic Potential Figure 4 shows a crescent-shaped region, R that lies inside the disk D1 � {(x, y) 冟 (x � 2)2 � y 2 4} and outside the disk, D2 � {(x, y) 冟 (x � 1)2 � y 2 1}. Suppose that the electrostatic potential along the, inner circle is kept at 50 volts and the electrostatic potential along the outer circle is, kept at 100 volts. Then the electrostatic potential at any point (x, y) in R is given by, U(x, y) � 150 �, volts., , 200x, x 2 � y2
Page 75 :
13.3, y, , 1063, , a. Compute Ux(x, y) and Uy(x, y)., b. Compute Ux(3, 1) and Uy(3, 1) and interpret your results., U � 50, D2, , 0, , Partial Derivatives, , U � 100, D1, , 2, , 4, , x, , Solution, a. Ux(x, y) �, , x, , c150 �, , 200x, x �y, 2, , (x 2 � y 2), , x, , ��, FIGURE 4, The electrostatic potential inside the, crescent-shaped region is U(x, y)., , ��, Uy(x, y) �, , 2, , d��, , 200x, , x x � y2, 2, , (200x) � 200x, , x, , b, , (x 2 � y 2), , (x 2 � y 2)2, 200(x 2 � y 2) � 200x(2x), , y, , (x 2 � y 2)2, c150 �, , � �200x, , y, , 200x, x �y, 2, , 2, , d��, , � 200x(x 2 � y 2)�2(2y) �, 200(9 � 1), (9 � 1)2, , �, , 200(x 2 � y 2), (x 2 � y 2)2, , 200x, a, b, y x 2 � y2, , (x 2 � y 2)�1, , � �200x(�1)(x 2 � y 2)�2, , b. Ux(3, 1) �, , a, , � 16, , y, , (x 2 � y 2), , 400xy, (x � y 2)2, , and, , 2, , Uy(3, 1) �, , 400(3)(1), (9 � 1)2, , � 12, , This tells us that the rate of change of the electrostatic potential at the point (3, 1), in the x-direction is 16 volts per unit change in x with y held fixed at 1, and the, rate of change of the electrostatic potential at the point (3, 1) in the y-direction, is 12 volts per unit change in y with x held fixed at 3., , EXAMPLE 5 A Production Function The production function of a certain country is, given by, f(x, y) � 20x 2>3y 1>3, billion dollars, when x billion dollars of labor and y billion dollars of capital are spent., a. Compute fx(x, y) and fy(x, y)., b. Compute fx(125, 27) and fy(125, 27) , and interpret your results., c. Should the government encourage capital investment rather than investment in, labor to increase the country’s productivity?, Solution, a. fx(x, y) �, fy(x, y) �, , 2, 40 y 1>3, (20x 2>3y 1>3) � (20) a x �1>3 b (y 1>3) �, a b, x, 3, 3 x, 1, 20 x 2>3, (20x 2>3y 1>3) � (20x 2>3) a y �2>3 b �, a b, y, 3, 3 y
Page 76 :
1064, , Chapter 13 Functions of Several Variables, , b. fx(125, 27) �, , 40 27 1>3 40 3, a, b �, a b�8, 3 125, 3 5, , This says that the production is increasing at the rate of $8 billion per billion dollar increase in labor expenditure when the labor expenditure stands at $125 billion (capital expenditure held constant at $27 billion)., Next,, fy(125, 27) �, , 20 125 2>3 20 25, 14, a, b �, a b � 18, 3 27, 3 9, 27, , This tells us that production is increasing at the rate of approximately $18.5 billion per billion dollar increase in capital outlay when the capital expenditure, stands at $27 billion (with labor expenditure held constant at $125 billion)., c. Yes. Since a unit increase in capital expenditure results in a greater increase in, production than a unit increase in labor, the government should encourage spending on capital rather than on labor., Sometimes we have available only the contour map of a function f. In such instances, we can use the contour map to help us estimate the partial derivatives of f at a specified point, as the following example shows., , EXAMPLE 6 Figure 5 shows the contour map of a function f. Use it to estimate, fx(3, 1) and fy(3, 1) ., y, , 8, �1, , 2, 0, , 6, , 10, , 2, 12, , 4, 0, , 2, , 4 14, , 6, , x, , 16, , FIGURE 5, A contour map of f, , Solution To estimate fx(3, 1), we start at the point (3, 1), where the value of f at (3, 1), can be read off from the contour map: f(3, 1) � 8. Then we proceed along the positive x-axis until we arrive at the point on the next level curve whose location is approximately (3.8, 1). Using the definition of the partial derivative, we find, fx(3, 1) ⬇, , f(3.8, 1) � f(3, 1), 10 � 8, �, � 2.5, 3.8 � 3, 0.8, , Similarly, starting at the point (3, 1) and moving along the positive y-axis, we find, fy(3, 1) ⬇, , f(3, 3) � f(3, 1), 6�8, �, � �1, 3�1, 2
Page 77 :
13.3, , Partial Derivatives, , 1065, , Implicit Differentiation, EXAMPLE 7 Suppose z is a differentiable function of x and y that is defined implicitly by x 2 � y 3 � z � 2yz 2 � 5. Find z> x and z> y., Solution, , Differentiating the given equation implicitly with respect to x, we find, x, , (x 2 � y 3 � z � 2yz 2) �, , 2x �, , x, , (5), , z, z, � 2ya2z b � 0, x, x, , Remember that y is, treated as a constant., , z, (4yz � 1) � 2x � 0, x, and, z, 2x, �, x, 1 � 4yz, Next, differentiating the given equation with respect to y, we obtain, y, 3y 2 �, , (x 2 � y 3 � z � 2yz 2) �, , (5), , z, z, � 2ya2z b � 2z 2 � 0, y, y, , 3y 2 �, and, , y, , z, (1 � 4yz) � 2z 2 � 0, y, 3y 2 � 2z 2, z, �, y, 1 � 4yz, , Partial Derivatives of Functions of More Than Two Variables, The partial derivatives of a function of more than two variables are defined in much, the same way as the partial derivatives of a function of two variables. For example,, suppose that f is a function of three variables defined by w � f(x, y, z). Then the partial derivative of f with respect to x is defined as, f, f(x � h, y, z) � f(x, y, z), w, �, � lim, x, x h→0, h, where y and z are held fixed, provided that the limit exists. The other two partial derivatives, f> y and f> z, are defined in a similar manner., , Finding the Partial Derivative of a Function of More Than Two Variables, To find the partial derivative of a function of more than two variables with respect, to a certain variable, say x, we treat all the other variables as if they are constants and differentiate with respect to x in the usual manner.
Page 78 :
1066, , Chapter 13 Functions of Several Variables, , EXAMPLE 8 Find, a. fx if f(x, y, z) � x 2y � y 2z � xz, , b. h w if h(x, y, z, w) �, , xw 2, y � sin zw, , Solution, a. To find fx, we treat y and z as constants and differentiate f with respect to x to, obtain, fx �, , x, , (x 2y � y 2z � xz) � 2xy � z, , b. To find h w, we treat x, y, and z as constants and differentiate h with respect to w,, obtaining, xw 2, b, w y � sin zw, a, , hw �, , (y � sin zw), , w, , �, , �, �, , (xw 2) � xw 2, , w, , (y � sin zw), Use the Quotient Rule., , (y � sin zw)2, (y � sin zw)(2xw) � xw 2 c0 � cos zw ⴢ, , w, , (zw)d, Use the Chain Rule., , (y � sin zw)2, 2xw(y � sin zw) � xw 2z cos zw, (y � sin zw)2, , xw(2y � 2 sin zw � wz cos zw), , �, , (y � sin zw)2, , Higher-Order Derivatives, Consider the function z � f(x, y) of two variables. Each of the partial derivatives f> x, and f> y are functions of x and y. Therefore, we may take the partial derivatives of, these functions to obtain the four second-order partial derivatives, 2, , f, , x, , 2, , �, , x, , a, , 2, , f, b,, x, , f, , y x, , �, , y, , a, , f, b,, x, , 2, , f, , x y, , �, , x, , a, , f, b,, y, , and, , 2, , f, , y, , 2, , �, , y, , a, , f, b, y, , (See Figure 6.), , ∂, ∂x, , ∂f, ∂x, , f, ∂, ∂y, , FIGURE 6, The differential operators are shown, on the limbs of the tree diagram., , ∂f, ∂y, , ∂, ∂x, , ∂ ∂f, ∂2f, = 2, ∂x ∂x, ∂x, , ∂, ∂y, , ∂ ∂f, ∂2f, =, ∂y ∂x, ∂y ∂x, , (, (, (, (, , ∂, ∂x, , ), ), ), ), , ∂ ∂f, ∂2f, =, ∂x ∂y, ∂x ∂y, ∂ ∂f, ∂2f, = 2, ∂y ∂y, ∂y, , ∂, ∂y, , Before we turn to an example, let’s introduce some additional notation for the, second-order partial derivatives of f :, 2, , f, , x, , 2, , 2, , � fxx, , f, , y x, , 2, , � fxy, , f, , x y, , 2, , � fyx, , f, , y2, , � fyy
Page 79 :
13.3, , Partial Derivatives, , 1067, , Note the order in which the derivatives are taken: Using the notation 2f>( y x), we, differentiate first with respect to x—the independent variable that appears first when, read from right to left. In the notation fxy we also differentiate first with respect to x—, the independent variable that appears first when read from left to right. The derivatives, fxy and fyx are called mixed partial derivatives., Note If f is defined by the equation z � f(x, y), then the four partial derivatives of f, are also written, z xx z xy z yx, , and, , z yy, , EXAMPLE 9 Find the second-order partial derivatives of f(x, y) � 2xy 2 � 3x 2 � xy 3., Solution, , We first compute the first-order partial derivatives, fx �, , Historical Biography, , x, , (2xy 2 � 3x 2 � xy 3) � 2y 2 � 6x � y 3, , SPL/Photo Researchers, Inc., , and, fy �, , y, , (2xy 2 � 3x 2 � xy 3) � 4xy � 3xy 2, , Then differentiating each of these functions, we obtain, fxx �, , ALEXIS CLAUDE CLAIRAUT, (1713–1765), Alexis Claude Clairaut was one of twenty, children born to his mother but the only to, survive to adulthood. His father, a mathematics teacher in Paris, educated his son, at home with very high standards: Alexis, was taught to read using Euclid’s Elements., As a result of both nature and nurture,, Clairaut turned out to be a very precocious, mathematician. He studied calculus by the, age of 10 and wrote an original mathematical paper at 13. At 18 he published his first, paper; he also became the youngest member ever admitted to the prestigious Academie des Sciences. Clairaut excelled in, many areas of mathematics, including, geometry, calculus, and celestial mechanics. He was the first to prove the prediction, by Isaac Newton and the astronomer Christiaan Huygens that the earth is an oblate, ellipsoid. Clairaut also accurately predicted, the return of Halley’s comet in 1759, a prediction that made him famous. Clairaut, developed the notation for partial derivatives that we still use today, and he was, the first to prove that mixed second-order, partial derivatives of a function at a point, are equal if the derivatives are continuous, at that point., , fxy �, fyx �, fyy �, , x, y, x, y, , fx �, fx �, fy �, fy �, , x, y, x, y, , (2y 2 � 6x � y 3) � �6, (2y 2 � 6x � y 3) � 4y � 3y 2, (4xy � 3xy 2) � 4y � 3y 2, (4xy � 3xy 2) � 4x � 6xy, , Notice that the mixed derivatives fxy and fyx in Example 9 are equal. The following, theorem, which we state without proof, gives the conditions under which this is true., , THEOREM 1 Clairaut’s Theorem, If f(x, y) and its partial derivatives fx, fy, fxy, and fyx are continuous on an open, region R, then, fxy(x, y) � fyx(x, y), for all (x, y) in R., , A function u of two variables x and y is called a harmonic function if u xx � u yy � 0, for all (x, y) in the domain of u. Harmonic functions are used in the study of heat conduction, fluid flow, and potential theory. The partial differential equation u xx � u yy � 0, is called Laplace’s equation, named for Pierre Laplace (1749–1827).
Page 81 :
13.3, , 13.3, , 1069, , CONCEPT QUESTIONS, , 1. a. Define the partial derivatives of a function of two variables, x and y, with respect to x and with respect to y., b. Give a geometric and a physical interpretation of fx(x, y)., 2. Let f be a function of x and y. Describe a procedure for finding fx and fy., , 13.3, , Partial Derivatives, , 3. Suppose F(x, y, z) � 0 defines x implicitly as a function of y, and z; that is, x � f(y, z). Describe a procedure for finding, x> z. Illustrate with an example of your choice., 4. If f is a function of x and y, give a condition that will guarantee that fxy(x, y) � fyx(x, y) for all (x, y) in some open region., , EXERCISES, , 1. Let f(x, y) � x 2 � 2y 2., a. Find fx(2, 1) and fy(2, 1)., b. Interpret the numbers in part (a) as slopes., c. Interpret the numbers in part (a) as rates of change., 2. Let f(x, y) � 9 � x 2 � xy � 2y 2., a. Find fx(1, 2) and fy(1, 2)., b. Interpret the numbers in part (a) as slopes., c. Interpret the numbers in part (a) as rates of change., , (b), , 2, 2.0, 1.5, 1.0, 0.5, 0.0, �2, , 3. Determine the sign of f> x and f> y at the points P, Q,, and R on the graph of the function f shown in the figure., , 1, , 0, , z, , x, , �1, , 0, y, , (c), z, 1, , 2, , �1 �2, , 0, , 1, , 2, , �1 �2, , Q, , P, , 2, R, , z, 0, �2, , y, �2, , x, , 4. The graphs of a function f and its partial derivatives fx and fy, are labeled (a), (b), and (c). Identify the graphs of f, fx, and, fy, and give a reason for your answer., (a), 2, , 1, , 0 �1, , �2, , 0, y, , 1, , 2, , 5. The figure below shows the contour map of the function T, (measured in degrees Fahrenheit) giving the temperature at each, point (x, y) on an 8 in. 5 in. rectangular metal plate. Use it, to estimate the rate of change of the temperature at the point, (3, 2) in the positive x-direction and in the positive y-direction., y (in.), 5, , 0.5, z, 0, , 4, 75, , 80, , 3, , 105, , 110, , �0.5, �2, , x, , �1, , 100 95, , 85, , 90, , 2, x, , �1, , 0, y, , 1, , 2, , V Videos for selected exercises are available online at www.academic.cengage.com/login., , 1, 0, , 1, , 2, , 3, , 4, , 5, , 6, , 7, , 8, , x (in.)
Page 82 :
1070, , Chapter 13 Functions of Several Variables, In Exercises 46–49, show that the mixed partial derivatives fxy, and fyx are equal., , In Exercises 6–29, find the first partial derivatives of the, function., 7. f(x, y) � 2x 2 � 3xy � y 2, , 6. f(x, y) � 3x � 4y � 2, 8. z � 2x 3 � 3x 2y 3 � xy 2 � 2x, 9. z � x 1y, , 10. f(x, y) � (2x 2 � y 3)4, , 46. f(x, y) � x 2 � 2x 2y � y 3, , 47. f(x, y) � x sin2 y � y 2 cos x, , 48. f(x, y) � e�2x cos 3y, , 49. f(x, y) � tan�1(x 2 � y 3), , In Exercises 50–53, show that the mixed partial derivatives fxyz ,, fyxz , and fzyx are equal., , 11. t(r, s) � 1r � s 2, , 12. h(u, √) � ln(u 2 � √2), , 13. f(x, y) � xey>x, , 14. f(x, y) � ex cos y � ey sin x, , 50. f(x, y, z) � x 2y 3 � y 2z 3, , 16. f(x, y) � 23 � 2x � y, , 51. f(x, y, z) � 29 � x 2 � 2y 2 � z 2, , �1, , 15. z � tan (x � y ), 17. t(u, √) �, , 2, , 2, , 2, , 52. f(x, y, z) � ln(x � 2y � 3z), , u√, u 2 � √3, , 18. f(x, y) � sinh xy, , x, 19. t(x, y) � x cosh, y, , 20. z � ln(e � y ), , 21. f(x, y) � y, , x, , 53. f(x, y, z) � e�x cos yz, , 2, , 2, , y, , 22. f(x, y) �, , 2, , 54. The figure shows the contour map of a function f. Use it to, determine the sign of (a) fx, (b) fy, (c) fxx, (d) fxy, and (e) fyy, at the point P., , x, y, , 冮 cos t dt, , 23. f(x, y) �, , x, , 冮 te, , �t, , dt, , y, , x, , 2, , 24. f(x, y, z) � 2x 3 � 3xy � 2yz � z 2, 25. t(x, y, z) � 1xyz, , 26. f(u, √, w) � ue � √e � we, , 27. u � xey>z � z 2, , 28. u � x sin, , u, , √, , u, , y, x�z, , P, , 4, 6, 8, 10, , 29. f(r, s, t) � rs ln st, 0, , x, , In Exercises 30–33, use implicit differentiation to find z> x and, z> y., 31. xey � ye�x � ez � 10, , 30. x 2y � xz � yz 2 � 8, , 32. 2 cos(x � 2y) � sin yz � 1 � 0, 33. ln(x 2 � z 2) � yz 3 � 2x 2 � 10, , 55. u � e�t sin, , In Exercises 34–39, find the second partial derivatives of the, function., 34. f(x, y) � x � 2x y � y � 3x, 4, , 2 3, , 4, , x, c, , 2k2t, , 56. u � e�c, , In Exercises 57 and 58, show that the function satisfies the, one-dimensional wave equation u tt � c2u xx., 58. u � sin(kct) sin(kx), , 36. z � xe2y � ye2x, 37. w � cos(2u � √) � sin(2u � √), 39. h(x, y) � tan�1, , y, x, , In Exercises 59–64, show that the function satisfies the, two-dimensional Laplace’s equation u xx � u yy � 0., , 40. f(x, y) � x 3 � y 3 � 3x 2y 2 � 2x � 3y � 4;, 42. f(x, y, z) � ln(x 2 � y 2 � z 2);, , fyxz, , 3, , 43. z � x cos y � y sin x;, 3, , 44. p � eu√w;, , z, x y x, , p, u w √, , 45. h(x, y, z) � e cos(y � 2z);, x, , fxyx, , fxxx, , 60. u �, , 61. u � ln2x 2 � y 2, , 62. u � e�x cos y � e�y cos x, , 63. u � tan�1, , x 2 � y2, , y, x, , 64. u � cosh y sin x � sinh y cos x, In Exercises 65 and 66, show that the function satisfies the, three-dimensional Laplace’s equation u xx � u yy � u zz � 0., 65. u � x 2 � 3xy � 2y 2 � 3z 2 � 4xyz, , h zzy, , x, , 59. u � 3x 2y � y 3, , In Exercises 40–45, find the indicated partial derivative., 41. f(x, y) � x 4 � 2x 2y 2 � xy 3 � 2y 4;, , cos kx, , 57. u � cos(x � ct) � 2 sin(x � ct), , 35. t(x, y) � x 3y 2 � xy 3 � 2x � 3y � 1, , 38. z � 2x 2 � y 2, , In Exercises 55 and 56, show that the function satisfies the, one-dimensional heat equation u t � c2u xx., , 66. u � (x 2 � y 2 � z 2)�1>2
Page 83 :
13.3, y, 67. Show that the function z � 2x 2 � y 2 tan�1 satisfies the, x, z, z, equation x, �y, � z., x, y, y, 68. Show that the function u � 20x 2 cos satisfies the equation, x, u, u, �y, � 2u., x, x, y, , a. Compute Tx 1 12, 12 2 , and interpret your result., b. Find the rate of change of the temperature at the point, P 1 12, 12 2 in the y-direction., y, , T � 100, , 69. According to the ideal gas law, the volume V (in liters), of an ideal gas is related to its pressure P (in pascals) and, temperature T (in kelvins) by the formula, V�, , kT, P, , where k is a constant. Compute V> T and V> P if, k � 8.314, T � 300, and P � 125, and interpret your, results., 70. Refer to Exercise 69. Show that, T, P, V, ⴢ, ⴢ, � �1, T, P, V, 71. The total resistance R (in ohms) of three resistors with, resistances of R1, R2, and R3 ohms connected in parallel, is given by the formula, 1, 1, 1, 1, �, �, �, R, R1, R2, R3, Find R> R1 and interpret your result., 72. The height of a hill (in feet) is given by, h(x, y) � 20(16 � 4x 2 � 3y 2 � 2xy � 28x � 18y), where x is the distance (in miles) east and y the distance, (in miles) north of Bolton. If you are at a point on the hill, 1 mile north and 1 mile east of Bolton, what is the rate of, change of the height of the hill (a) in a northerly direction, and (b) in an easterly direction?, 73. Profit Versus Inventory and Floor Space The monthly profit (in, dollars) of the Barker Department Store depends on its level, of inventory x (in thousands of dollars) and the floor space y, (in thousands of square feet) available for display of its merchandise, as given by the equation, P(x, y) � �0.02x 2 � 15y 2 � xy � 39x � 25y � 15,000, Find P> x and P> y when x � 5000 and y � 200, and, interpret your result., 74. Steady-State Temperature Consider the upper half-disk, H � {(x, y) 冟 x 2 � y 2 1, y � 0} (see the figure). If the, temperature at points on the upper boundary is kept at, 100°C and the temperature at points on the lower boundary, is kept at 50°C, then the steady-state temperature at any, point (x, y) inside the half-disk is given by, T(x, y) � 100 �, , 1 � x 2 � y2, 100, tan�1, p, 2y, , 1071, , Partial Derivatives, , �1 T � 50, , 0, , x, , 1, , 75. Electric Potential A charge Q (in coulombs) located at the origin of a three-dimensional coordinate system produces an, electric potential V (in volts) given by, V(x, y, z) �, , kQ, 2x � y 2 � z 2, 2, , where k is a positive constant and x, y, and z are measured, in meters. Find the rate of change of the potential at the, point P(1, 2, 3) in the x-direction., 76. Surface Area of a Human The formula, S � 0.007184W 0.425H 0.725, gives the surface area S of a human body (in square meters), in terms of its weight W (in kilograms) and its height H (in, centimeters). Compute S> W and S> H when W � 70, and H � 180, and interpret your results., 77. Arson Study A study of arson for profit conducted for a, certain city found that the number of suspicious fires is, approximated by the formula, N(x, y) �, , 12021000 � 0.03x 2y, (5 � 0.2y)2, 0 x, , 150,, , 5, , y, , 35, , where x denotes the number of persons per census tract and, y denotes the level of reinvestment in conventional mortgages by the city’s ten largest banks measured in cents per, dollars deposited. Compute N> x and N> y when, x � 100 and y � 20, and interpret your results., 78. Production Functions The productivity of a Central American, country is given by the function, f(x, y) � 20x 3>4y 1>4, when x units of labor and y units of capital are used., a. What are the marginal productivity of labor and the, marginal productivity of capital when the amounts, expended on labor and capital are 256 units and, 16 units, respectively?, b. Should the government encourage capital investment, rather than increased expenditure on labor at this time, to increase the country’s productivity?
Page 84 :
1072, , Chapter 13 Functions of Several Variables, , 79. Wind Chill Factor A formula that meteorologists use to, calculate the wind chill temperature (the temperature that, you would feel in still air that is the same as the actual, temperature when the presence of wind is taken into consideration) is, T � f(t, s) � 35.74 � 0.6125t � 35.75s 0.16 � 0.4275ts 0.16, s�1, where t is the air temperature in degrees Fahrenheit and s is, the wind speed in mph., a. What is the wind chill temperature when the actual air, temperature is 32°F and the wind speed is 20 mph?, b. What is the rate of change of the wind chill temperature, with respect to the wind speed if the temperature is 32°F, and the wind speed is 20 mph?, 80. Wind Chill Factor The wind chill temperature is the temperature that you would feel in still air that is the same as the, actual temperature when the presence of wind is taken into, consideration. The following table gives the wind chill temperature T � f(t, s) in degrees Fahrenheit in terms of the, actual air temperature t in degrees Fahrenheit and the wind, speed s in mph., , Wind speed (mph), , Actual air, temperature (ºF), , t, , s, , 30, , 10, , 15, , 20, , 25, , 30, , 35, , 40, , 21.2, , 19.0, , 17.4, , 16.0, , 14.9, , 13.9, , 13.0, , 32, , 23.7, , 21.6, , 20.0, , 18.7, , 17.6, , 16.6, , 15.8, , 34, , 26.2, , 24.2, , 22.6, , 21.4, , 20.3, , 19.4, , 18.6, , 36, , 28.7, , 26.7, , 25.2, , 24.0, , 23.0, , 22.2, , 21.4, , 38, , 31.2, , 29.3, , 27.9, , 26.7, , 25.7, , 24.9, , 24.2, , 40, , 33.6, , 31.8, , 20.5, , 29.4, , 28.5, , 27.7, , 82. a. Use the result of Exercise 81 to find fx 1 1, p2 2 if, f(x, y) � x 2 cos xy., b. Verify the result of part (a) by evaluating fx(x, y) at 1 1, p2 2 ., cas In Exercises 83 and 84, use the result of Exercise 81 and a cal-, , culator or computer to find the partial derivative., 83. fx(2, 1) if f(x, y) � ln 1 exy � cos2x 2 � y 2 2, sin pxy, , 1 1 � 2x 2 � y 3 2 3>2, , 84. fy(2, 1) if f(x, y) �, , 85. Cobb-Douglas Production Function Show that the Cobb-Douglas, production function P � kx ay 1�a, where 0 � a � 1, satisfies the equation, x, , P, P, �y, �P, x, y, , Note: This equation is called Euler’s equation., , 86. Let S be the surface with equation z � f(x, y), where f has, continuous first-order partial derivatives and P(x 0, y0, z 0) is, a point on S (see the figure). Let C1 and C2 be the curves, obtained by the intersection of the surface S with the planes, x � x 0 and y � y0, respectively. Let T1 and T2 be the tangent, lines to the curves C1 and C2 at P. Then the tangent plane to, the surface S at the point P is the plane that contains both, tangent lines T1 and T2., z, T1, v1, , n, , v2, , P, , T2, S, , 26.9, , C2, , C1, 0, , y0, , x0, , a. Estimate the rate of change of the wind chill temperature, T with respect to the actual air temperature when the, wind speed is constant at 25 mph and the actual air, temperature is 34°F., Hint: Show that it is given by, , f(36, 25) � f(34, 25), T, (34, 25) ⬇, t, 2, b. Estimate the rate of change of the wind chill temperature, T with respect to the wind speed when the actual air, temperature is constant at 34°F and the wind speed is, 25 mph., Source: National Weather Service., , 81. Let f be a function of two variables., a. Put t(x) � f(x, b) , and use the definition of the derivative of a function of one variable to show that, fx(a, b) � t¿(a) ., b. Put h(y) � f(a, y), and show that fy(a, b) � h¿(b)., , x, , (x0, y0), , y, , a. Show that the vectors v1 � i � fx(x 0, y0)k and, v2 � j � fy(x 0, y0)k are parallel to T1 and T2, respectively., b. Using the result of part (a), find a vector n that is normal, to both v1 and v2., c. Use the result of part (b) to show that an equation of the, tangent plane to S at P is, z � z 0 � fx(x 0, y0)(x � x 0) � fy(x 0, y0)(y � y0), 87. Use the result of Exercise 86 to find an equation of the tangent plane to the paraboloid z � x 2 � 14 y 2 at the point, (1, 2, 2) ., 88. Engine Efficiency The efficiency of an internal combustion, engine is given by, E � a1 �, , √ 0.4, b, V
Page 85 :
13.4, where V and √ are the respective maximum and minimum, volumes of air in each cylinder., a. Show that E> V � 0, and interpret your result., b. Show that E> √ � 0, and interpret your result., 89. A semi-infinite strip has faces that are insulated. If the edges, x � 0 and x � p of the strip are kept at temperature zero, and the base of the strip is kept at temperature 1, then the, steady-state temperature (that is, the temperature after a long, time) is given by, T(x, y) �, Find, , T, x, , 1 p2 , 1 2 and, , T, y, , 1073, , a. Find fx(x, y) and fy(x, y) for (x, y) � (0, 0)., b. Use the definition of partial derivatives to find fx(0, 0), and fy(0, 0) ., c. Show that fxy(0, 0) � �1 and fyx(0, 0) � 1., d. Does the result of part (c) contradict Theorem 1? Explain., 91. Does there exist a function f of two variables x and y, with continuous second-order partial derivatives, such that fx(x, y) � e2x(2 cos xy � y sin xy) and, fy(x, y) � �ye2x sin xy? Explain., 92. Show that if a function f of two variables x and y has continuous third-order partial derivatives, then fxyx � fyxx � fxxy., , 2, sin x, tan�1, p, sinh y, , 1 p2 , 1 2 , and interpret your results., , y, , In Exercises 93–96, determine whether the statement is true or, false. If it is true, explain why it is true. If it is false, give an, example to show why it is false., 93. If z � f(x, y) has a partial derivative with respect to x at the, point (a, b) , then, , T�0, , T�0, , π, , x, , 90. Let, xy(x 2 � y 2), x 2 � y2, 0, , f(x, b) � f(a, b), f, (a, b) � lim, x�a, x, x→a, 94. If f> y (a, b) � 0, then the tangent line to the curve, formed by the intersection of the plane x � a and the, surface z � f(x, y) at the point (a, b, f(a, b)) is horizontal;, that is, it is parallel to the xy-plane., , T�1, 0, , f(x, y) � •, , Differentials, , if (x, y) � (0, 0), if (x, y) � (0, 0), , 95. If fxx(x, y) is defined for all x and y and fxx(a, b) � 0 for, all x in the interval (a, b), then the curve C formed by the, intersection of the plane y � b and the surface z � f(x, y), is concave downward on (a, b)., 96. If f(x, y) � ln xy, then fxy(x, y) � fyx(x, y) for all (x, y) in, D � {(x, y) 冟 xy � 0}., , 13.4 Differentials, Increments, Recall that if f is a function of one variable defined by y � f(x), then the increment in, y is defined to be, ⌬y � f(x � ⌬x) � f(x), where ⌬x is an increment in x (Figure 1a). The increment of a function of two or more, variables is defined in an analogous manner. For example, if z is a function of two variables defined by z � f(x, y), then the increment in z produced by increments of ⌬x, and ⌬y in the independent variables x and y, respectively, is defined to be, ⌬z � f(x � ⌬x, y � ⌬y) � f(x, y), (See Figure 1b.), , (1)