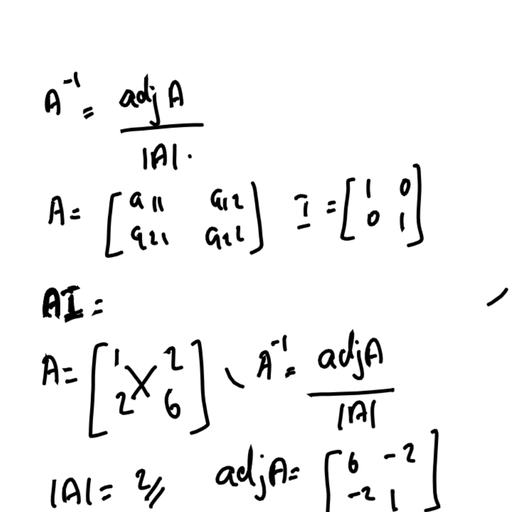Page 1 :
Chapter 1, , Derivatives and, Limits, Differentiation is one of the two fundamental operations of calculus., , Differential calculus describes and analyzes change. The position of a moving, object, the population of a city or a bacterial colony, the height of the sun in, the sky, and the price of cheese all change with time. Altitude can change with, position along a road; the pressure inside a balloon changes with temperature., To measure the rate of change in all these situations, we introduce in this, chapter the operation of differentiation., , 1 ."0,lntrodiaaetlon to the, , Derivative, Velocities and slopes are both derivatives., , This section introduces the basic idea of the derivative by studying two, problems. The first is the problem of finding the velocity of a moving object,, and the second is the problem of finding the slope of the line tangent to a, graph., To analyze velocity, imagine a bus which moves due east on a straight, highway. Let x designate the time in seconds that has passed since we first, observed the bus. (Using "x" for time rather than the more common "t" will, make it easier to compare velocities with slopes.) Suppose that after x seconds, the bus has gone a distance y meters to the east (Fig. 1.1.1). Since the distance, y depends on the time x, we have a distance function y = f(x). For example, if, Figure 1.1.1. What is the, velocity of the bus in terms, of its position?, , .r = time in seconds, , 20, , 40, , -b, , 20, , 40, , y m, , r, , t, , e, , r, , s, , A, , Starting position, , Copyright 1985 Springer-Verlag. All rights reserved.

Page 2 :
50, , Chapter 1 Derivatives and Limits, , f(x) happens to be f(x) = 2x2 for 0 < x ,< 5, then the bus has gone 2 - (3)*, = 18 meters after 3 seconds and 2 . (512 = 50 meters after 5 seconds., The velocity of the bus at any given moment, measured in meters per, second, is a definite physical quantity; it can be measured by a speedometer, on the bus or by a stationary radar device. Since this velocity refers to a single, instant, it is called the instantaneous velocity. Given a distance function such as, y = f(x) = 2x2, how can we calculate the instantaneous velocity at a specific, time x,, such as x, = 3 seconds? To answer this question, we will relate the, instantaneous velocity to the average velocity during short time intervals., Suppose that the distance covered is measured at time x, and again at a, later time x; these distances are yo = f(x,) and y = f(x). Let Ax = x - x,, designate the time elapsed between our two measurements.' Then the extra, distance covered is y -yo, which we designate by Ay = y -yo. The average velocity during the time interval Ax is defined simply as the distance, travelled divided by the elapsed time; that is, average velocity = Ay/Ax =, [ f(x) - f(xo)]/Ax. Since x = x, + Ax, we can also write, average velocity =, , f(x0 + Ax) - f(x0), Ax, , Example I, , A bus travels 2x2 meters in x seconds. Find Ax, Ay and the average velocity, during the time interval Ax for the following situations: (a) x, = 3, x = 4;, ( b ) x 0 = 3 , x =3.1; (c)x,= 3, x =3.01., , Soiiletlon, , (a) Ax = x - x, = 4 - 3 = 1 second, Ay = f(x, + Ax) - f(x,) = f(4) - f(3), = 2 .4' - 2 - 3' = 14 meters, average velocity = Ay/Ax = 14 meters per second; (b) Ax = 0.1, Ay = 1.22, average velocity = 12.2; (c) Ax = 0.01, Ay =, .1202, average velocity = 12.02 meters per second. A, If we specify the accuracy to which we want to determine the instantaneous, velocity, we can expect to get this accuracy by calculating the average velocity, Ay/Ax for Ax sufficiently small. As the desired accuracy increases, Ax may, need to be made even smaller; the exact velocity may then be described as the, number v which Ay/Ax approximates as Ax becomes very small. For instance, in Example 1, you might guess that the instantaneous velocity at, xo = 3 seconds is v = 12 meters per second; this guess is correct, as we will see, shortly., Our description of v as the number which Ay/Ax approximates for Ax, very small is a bit vague, because of the ambiguity in what is meant by, "approximates" and "very small." Indeed, these ideas were the subject of, controversy during the early development of calculus around 1700. It was, thought that Ax ultimately becomes '6infinitesimal,"and for centuries people, argued about what, if anything, "infinitesimal" might mean. Using the notion, of "limit," a topic taken up in the next section, one can resolve these, difficulties. However, if we work on an intuitive basis with such notions as, "approximates," "gets close to," "small," "very small," "nearly zero," etc., we, can solve problems and arrive at answers that will be fully justified later., , Example 2, , The bus has gone f(x) = 2x2 meters at time x (in seconds). Calculate its, instantaneous velocity at x, = 3., , ', , A is the capital Greek letter "delta," which corresponds to the Roman D and stands for, difference. The combination "Ax", read "delta-x", is not the product of A and x but rather a, single quantity: the difference between two values of x., , Copyright 1985 Springer-Verlag. All rights reserved.

Page 3 :
1.1 Introduction to the Derivative, , Solution, , 51, , We choose Ax arbitrarily and calculate the average velocity for a time interval, Ax starting at time x , = 3 :, , aY- - f ( 3, Ax, , + Ax) -f(3), Ax, , -, , 2(3 +, , AX)^ - 2 .3', Ax, , If we let Ax become very small in this last expression, 2 A x becomes small as, well, and so A y / A x = 12 -k 2 A x approximates 12. Thus the required instantaneous velocity at x, = 3 is 12 meters per second. Note how nicely the 18's, cancelled. This allowed us to divide through by Ax and avoid ending up with, a zero in the denominator. A, Warning, , In calculating what A y / A x approximates for Ax nearly zero, it usually does, no good to set Ax = 0 directly, for then we merely get 0 / 0 , which gives us no, information., The following more general procedure is suggested by Example 2., , To calculate the instantaneous velocity at x , when the position at time x, , 1. Form the average velocity over the interval from x , to x,, , + Ax:, , -2. Simplify your expression for A y / A x as much as possible, cancelling, Ax from numerator and denominator wherever you can., 3. Find the number v that is approximated by A y / A x for Ax small., , Example 3, , The position of a bus at time x is y = 3 x 2 + 8 x for x > 0 . (a) Find the, instantaneous velocity at an arbitrary positive time x,. (b) At what time is the, instantaneous velocity 1 1 meters per second?, , Solution, , (a) The calculation is similar to that of Example 2, except that x , no longer, has the specific value x , = 3. The average velocity for a time interval Ax, starting at x , is, , f ( x o + Ax> - f (xo), Ax, Ax, where f ( x ) = 3 x 2 + 8 x . Thus, Ay -, , As Ax gets close zero, the term 3 Ax gets close to zero as well, so A y / A x gets, close to (that is, approximates) 6 x o + 8. Thus our instantaneous velocity is, v = 6 x 0 + 8 meters per second at the positive time x,., , Copyright 1985 Springer-Verlag. All rights reserved.

Page 4 :
52, , Chapter "Ierivatives, , and Limits, , (b) We set the velocity equal to 11: 6x0 + 8 = 11. Solving for xo gives, x, = 4 second. A, The second problem we study is a geometric one-to find the slope of the line, tangent to the graph of a given function. We shall see that this problem is, closely related to the problem of finding instantaneous velocities., To solve the slope problem for the function y = f(x), we begin by, drawing the straight line which passes through the points (x,, f(x,)) and, (x, + Ax, f(xo + Ax)), where Ax is a positive number; see Fig. 1.1.2. This, straight Iine is called a secant line, and Ay/Ax = [f(xo + Ax) - f(xo)]/Ax is, its slope., As Ax becomes small, x, being fixed, it appears that the secant line comes, close to the tangent line, so that the slope Ay/Ax of the secant line comes, close to the slope of the tangent line. See Fig. 1.1.3., Figure 1.1.2. AylAx is the, slope of the secant line., , Figure 1.1.3. The secant, line comes close to the, tangent line as the second, point moves close to xo., , Given a functiony = f(x), the slope rn of the line tangent to its graph at, (x,, yo) is calculated as follows:, 1. Form the slope of the secant line:, , f (xo + Ax) - f (xo), , Example 4, , Solullon, , Calculate the slope of the tangent line to the graph of f(x) = x2 + 1 at, x, = - 1. Indicate your result on a sketch., We form the slope of the secant line:, , For Ax small, this approximates - 2, so the required slope is - 2. Figure 1.1.4, , Copyright 1985 Springer-Verlag. All rights reserved.

Page 5 :
I.I, Introduction to the Derivative, , Figure 1.1.4. The tangent, line toy = x2 + 1 at, x, = - 1 has slope - 2., , 53, , Y = x ~ +1, , shows the graph of the parabola y, line through the point (- 1,2). A, , =, , x2, , + 1. We have sketched the tangent, , We define the slope of the graph of the function f at (x,, f(xo)) to be the slope, of the tangent line there., Up to this point, we have drawn all the pictures with Ax positive., However, the manipulations in Examples 2, 3, and 4 are valid if Ax has any, sign, as long as Ax f 0. From now on we will allow Ax to be either positive or, negative., Comparing the two previous boxes, we see that the procedures for, calculating instantaneous velocities and for calculating slopes are actually, identical; for example, the velocity calculation of Example 2 also tells us the, slope m of y = 2 x 2 at (3,181, namely m = 12. We will later find that the same, procedure applies to many other situations. It is thus convenient and economical to introduce terms which apply to all the different situations: instead of, calling A y / A x an average velocity or the slope of a secant, we call it a, dvference quotient; we call the final number obtained a derivative rather than, an instantaneous velocity or a slope. We use the notation f'(xo) to designate, the derivative off at x,., , The Derivative, To calculate the derivative f'(xo) of a function y = f(x> at x,:, 1. Form the difference quotient, , Ay--, , f (xo + A x ) - f ( x o ), , Ax, Ax, 2. Simplify A y / A x , cancelling Ax if possible., 3. The derivative is the number f'(x,) that Ay/Ax approximates for A x, small., , This operation of finding a derivative is called dqferentiation., The reader should be aware that the precise version of Step 3 involves the, notion of a limit, which is discussed in the next section., Example 5, Solution, , Suppose that m is a constant. Differentiate f ( x ) = mx, , + 2 at x, = 10., , Here the function is linear, so the derivative should be equal to the slope:, f'(10) = rn. To see this algebraically, calculate, , Copyright 1985 Springer-Verlag. All rights reserved.

Page 6 :
54, , Chapter 1 Derivatives and Limits, , This approximates (in fact equals) m for Ax small, so f'(10) = m. A, Glancing back over our examples, we notice that all the functions have been, either linear or quadratic. By treating a general quadratic function, we can, check our previous results and point the way to the goal of developing general, rules for finding derivatives., , Let f(x) = ax2 + bx + c, where a , b, and c are constants, and let x, be, any real number. Then f'(x,) = 2ax0 b., , +, , To justify the quadratic function rule, we form the difference quotient, , -, , -, , a(x,, , + 4x12 + b(xo + Ax) + c - ax:, , -, , bx, - c, , Ax, , 2sx, Ax, , = 2ax0, , +a(, , +b +, , 4 ~ +) b~Ax, , Ax, a Ax., , As Ax approaches zero, a Ax approaches zero, too, so Ay/Ax approximates, 2ax, b. Therefore 2a.xo h is the derivative of ax2 + hx c at x = x,., , +, , Example 6, , +, , Find the derivative of f(x), , = 3x2, , +, , + 8x at (a) x, = - 2, , and (b) x,, , =, , Solution (a) Applying the quadratic function rule with a, , = 3, b = 8, c = 0, and x, =, -2, we find f'(-2) = 2(3)(-2), 8 = -4., (b) Taking a = 3, b = 8, c = 0 and x, = 5, we get f '(4) = 2 - 3 . (4) 8 = 11,, which agrees with our answer in Example 3(b). A, , +, , +, , If we set a = 0 in the quadratic function rule, we find that the derivative of, any linear function bx + c is the constant b, independent of x,: the slope of a, linear function is constant. For a general quadratic function, though, the, derivative f'(x,) does depend upon the point x, at which the derivative is, taken. In fact, we can considerf' as a new function; writing the letter x instead, of x,, we have f'(x) = 2ax b. We can rephrase the quadratic function rule, with x, replaced by x as in the following box, which also summarizes the, special cases a = 0 and a = 0 = b., , +, , The derivative of the linear function f(x) = bx, , +c, , The derivative of the constant function f ( x ), , is the zero function, , =c, , is the constant, , Copyright 1985 Springer-Verlag. All rights reserved.

Page 7 :
1.9 Introduction to the Derivative, , 55, , The next example illustrates the use of thinking of the derivative as a function., , +, , Example 7, , There is one point on the graph of the parabola y = f(x) = x 2 - 4x 5 where, the slope is zero, so that the tangent line is horizontal (Fig. 1.1.5). Find that, point using: (a) derivatives; and (b) algebra., , Solution, , (a) By the quadratic function rule with a = 1, b = -4, c = 5, the derivative, function is f'(x) = 2x - 4. For zero slope we have 0 = f'(x) = 2x - 4, i.e.,, x = 2. Then y = I, so our point is (2,l). This point is called the vertex of, the parabola., (b) Completing the square gives f(x) = x 2 - 4x + 4 1 = (x - 2)2 1. Now, (x - 212 is zero for x = 2 and positive othemise, so the parabola has its, lowest point at x = 2. It is plausible from the figure, and true, that this low, point is the point where the slope is zero. A, , " = x * -4x+5, , +, , I, , +, , ', , We conclude this section with some examples of standard terms and notations. When we are dealing with functions given by specific formulas, we often, omit the function names. Thus in Example 7(a) we can say "the derivative of, x2 - 4x + 5 is 2x - 4." Another point is that we can use letters different from, x, y, and f. For example, the area A of a circle depends on its radius r ; we can, write A = g(r) = ar2. The quadratic function rule with a = a , b = 0 = c, with f, replaced by g and with x replaced by r, tells us that g'(r) = 2ar. Thus for a, circle the derivative of the area function is the circumference function-a fact, whose geometric interpretation will be discussed in Section 2.2. Similarly, the, time is often denoted by t in velocity problems., , Example 8, , A stunt woman is on a moving passenger train. Her distance function is, 3t2 + t. On the adjacent track is a long moving freight train. The distance, function for the center of this freight train is t2 72. She must jump to the, freight train. What time is best?, , Figure 1.1.5. The vertex of, is the point, the, where its slope is zero., , +, , Solution, , The safest time to jump is when the stunt woman has the same velocity as the, freight train (see Fig. 1.1.6). Her instantaneous velocity u is the derivative of, , Figure 1.1.4. The stunt, woman should jump when, she has the same velocity as, the freight train., , +, , 3t2 t . By the quadratic function rule, v = 6t + 1; similarly the instantaneous, velocity of the freight train is 2t + 7. The velocities are equal when 21 + 7, = 6t + 1, i.e., t = 2 . That is the safest time. A, In this section, we have discussed the derivative, one of the two most basic, concepts of calculus. We showed how to find derivatives in some cases and, , Copyright 1985 Springer-Verlag. All rights reserved.

Page 8 :
58, , Chapter 1 Derivatives and Limits, , indicated a few of their applications. Before we can usefully discuss other, applications of derivatives, we need to develop efficient techniques for calculating them. The next section begins that task., , Exercises for Section 1.I, In Exercises 1-4, y represents the distance a bus has, travelled after x seconds. Find Ay and the average, velocity during the time interval Ax for the following, situations., (b) xo = 2, Ax = 0.01, (a) x, = 2, Ax = 0.5, (d) x, = 4, Ax = 0.01, (c) xo = 4, Ax = 0.1, 2. y = 3 x 2 + x, 1. y = x 2 + 3 x, 3. y = x 2 + l o x, 4. y = 2 x, In Exercises 5-8, f ( x ) is the number of meters a bus has, gone at a time x (in seconds). Find the instantaneous, velocity at the given time xo., 6. x 2 3 x ; xo = 4, 5. x 2 + 3 x ; xo = 2, 8. 3 x 2 + x ; x0 = 4, 7. 3 x 2 x ; x0 = 2, In Exercises 9-12, y is the position (measured in meters) of a bus at time x (in seconds). (a) Find the, instantaneous velocity at an arbitrary (positive) time x,., (b) At what time is the instantaneous velocity 10 meters, per second?, 10. y = 3x1 + x, 9. y = x 2 + 3 x, 12. y = 2 x, 11. y = ~ 2 +, lox, In Exercises 13-16, use the A y / A x method of Example, 4 to find the slope of the tangent line to the graph of, the given function at the given point. Sketch., 13. y = x 2 ; xo = 1, 14. y = - x 2 ; x o = 2, 15. y = 5 x 2 - 3 x 1 ; xo = O, 16. y = x + 1 - x 2 ; x, = 2, In Exercises 17-20 use the A y / A x method of Example, 5 to compute the derivative of f ( x ) at x,; a is a constant, in each case., 17. f ( x ) = a x 2; xo=O, 18. f ( x ) = 2x + a ; xo = 0, 19. f ( x ) = ax2; x, = 1, 20. f ( x ) = 8 x 2 a ; x, = 2, In Exercises 21-24, use the quadratic function rule to, find the derivative of the given function at the indicated, point., 21. f ( x ) = x 2 X - 1 ; X o = 1, 22. f ( x ) = x 2 - x ; x, = 2, 23. f ( x ) = 3 x 2 + x - 2; x, = - 2, 24. f ( x ) = - 3 x 2 - x + l ; x o = - 1, In Exercises 25-28, find the vertex of the given parabola using (a) derivatives and (b) algebra., 25. y = x 2 - 16x 2, 26. y = x 2 8 x 2, 27. y = - 2 x 2 - 8 x - 1, 28. y = - 2 x 2 - 3 x + 5, Gifferentiate the functions in Exercises 29-36 using the, quadratic function rule., 29.f(x)=x2+3x-1, 30. f ( x ) = - 3 x + 4, 31. f ( x ) = ( x - l)(x 1) 32. f ( x ) = (9 - x)(l - x ), 33. g(r) = -4t2 + 3t + 6 34. g(r) = ?rr2+ 3, 35. g(s) = 1 - s2, 36. h ( t ) = 3 t 2 - . S t + 9, , +, , +, , +, , +, , +, , +, , +, + +, , +, , 37. Inspector Clumseaux is on a moving passenger, train. His distance function is 2t2 31. On the, adjacent track is a long moving freight train; the, distance function for the center of the freight, train is 3t2 + t. What is the best time for him to, jump to the freight train?, 38. Two trains, A and B, are moving on adjacent, tracks with positions given by the functions A ( t ), = t 2 + t + 5 and B ( t ) = 3t + 4. What is the best, time for a hobo on train B to make a moving, transfer to train A?, 39. An apple falls from a tall tree toward the earth., After t seconds, it has fallen 4.9t2 meters. What, is the velocity of the apple when t = 3?, 40. A rock thrown down from a bridge has fallen, 4t + 4.9t2 meters after t seconds. Find its velocity at t = 3., 41. f ( x ) = x 2 - 2; find f'(3), 42. f ( x ) = - 13x2 - 9 x + 5; find f'(1), 43. f ( x ) = 1 ; find f'(7), 44. g ( s ) = 0 ; find g'(3), 45. k ( y ) = ( y + 4 ) ( y - 7 ) ; find k ' ( - 1), 46. x ( f ) = 1 - f 2 ; find xl(0), 47. f ( x ) = - x + 2; find f'(3.752764), 48. g(a) = 10a - 8; find g'(3.1415), In Exercises 49-54, find the derivative of each of the, given functions by finding the value approximated by, A y / A x for Ax small:, 49. 4 x 2 3 x 2, 50. ( x - 3)(x + I ), 51. 1 - x 2, 52. - x 2, 53. - 2 x 2 + 5 x, 54. 1 - x, 55. Let f ( x ) = 2 x 2 3 x + 1 . (a) For which values of, x is f'(x) negative, positive, and zero? (b) Identify these points on a graph off., 56. Show that two quadratic functions which have, the same derivative must differ by a constant., 57. Let A ( x ) be the area of a square of side length x ., Show that A ' ( x ) is half the perimeter of the, square., 58. Let A ( r ) be the area of a circle of radius r. Show, that A f ( r ) is the circumference., 59. Where does the line tangent to the graph of, y = x 2 at x, = 2 intersect the x axis?, 60. Where does the line tangent to the graph of, y = 2 x 2 - 8x 1 at x, = 1 intersect they axis?, 61. Find the equation of the line tangent to the, graph of f ( x ) = 3x2 + 4 x + 2 at the point where, xo = 1. Sketch., 62. Find the tangent line to the parabola y = x 2 3 x + 1 when x, = 2. Sketch., *63. Find the lines through the point (4,7) which are, tangent to the graph of y = x2. Sketch. (Hint:, Find and solve an equation for the x coordinate, of the point of tangency.), , +, , + +, , +, , +, , Copyright 1985 Springer-Verlag. All rights reserved.

Page 9 :
1.2 Limits, , s64. Given a point (x,y), find a general rule for, determining how many lines through the point, are tangent to the parabola y = x2., r65. Let R be any point on the parabola y = x2., Draw the horizontal line through R and draw the, perpendicular to the tangent line at R. Show that, the distance between the points where these lines, cross the y axis is equal to 4, regardless of the, value of x. (Assume, however, that x + 0.), r66. If j(x) = ax2 + bx + c = a(x - r)(x - s) ( r and, s are the roots off), show that the values of f'(x), at r and s are negatives of one another. Explain, this by appeal to the symmetry of the graph., s67. Using your knowledge of circles, sketch the, Use this to guess the, graph of f(x) = JGf., values of f'(0) and f'(Q)., *68. A trained flea crawls along the parabola y = x 2, in such a way that its x coordinate at time t is, 2t + 1. The sun is shining from the east (positive, x axis) so that a shadow of the flea is projected, , 57, , on a wall built along the y axis. m a t is the, velocity of this shadow when t = 3?, r69. A ball is thrown upward at r = 0; its height in, meters until it strikes the ground is 24.5t - 4.9t2, when the time is t seconds. Find:, (a) The velocity at t = 0,1,2,3,4,5., (b) The time when the ball is at its highest, point., (c) The time when the velocity is zero., (d) The time when the ball strikes the ground., *70. A toolbox falls from a building, its height y in, feet from the ground after t seconds being given, by y q 100 - 16t2., (a) Find the impact time t*, i.e., the positive, time for which y = 0., (b) Find the impact velocity, i.e., the velocity, at t * ., (c) The momentum p is defined by p = Wu/32,, where W is the weight in pounds, and u is, the velocity in feet per second. Find the, impact momentum for a 20-lb toolbox., , The limit of a function f ( t ) at a point x = x , is the value which f ( x ) approximates fir x close to x,,., In this section, we introduce limits and study their properties. In the following, sections, we will use limits to clarify statements such as " A y / A x approximates, f'(x,) for Ax small," and to systematize the computing of derivatives. Some, technical points in the theory of limits have been deferred to Chapter 11,, where limits are needed again for other purposes. Readers who wish to see, more of the theory now can read Section 11.1 together with the present, section., We illustrate the idea of a limit by looking at the function, , which is defined for all real numbers except 3. Computing values of f ( x ) for, some values of x near 3, we obtain the following tables:, , It appears that, as x gets closer and closer to x , = 3 , f ( x ) gets closer and closer, to 5, i.e., f ( x ) approximates 5 for x close to 3. As in our discussion of the, derivative, it does no good to set x = 3, because f ( 3 ) is not defined. In the, , Copyright 1985 Springer-Verlag. All rights reserved.

Page 10 :
58, , Chapter 1 Derivatives and Limits, , special case we are considering, there is another way to see that f ( x ) approximates 5:, , The cancellation of ( x - 3 ) is valid for x # 3. Now for x close to 3 , 2 x - 1, approximates 2 . 3 - 1 = 5. Note that after cancelling x - 3 , the function, becomes defined at x, = 3., In general, suppose that we have a function f ( x ) and are interested in its, behavior near some value x,. Assume that f ( x ) is defined for all x near x,, bui, not necessarily at x = x , itself. If the value f ( x ) off approximates a number I, as x gets close to a number xo, we say that " I is the limit of f ( x ) as x, , Figure 1.2.1. The notion of, limit: as x approaches x,, f(x) gets near to I., , approaches x," or " f ( x ) approaches 1 as x approaches x,." See Fig. 1.2.1. Two, usual notations for this are, , f(x)-+I, lim f ( x ), , X--SXi,, , as x + x ,, , =, , I., , For example, the discussion above suggests that, , 2x2-7x+3+5, x-3, that is, lim 2 x 2 - 7 x + 3, x -3, , as x + 3 ;, , = 5., , x-3, , Example 1, , Solullon, , Using numerical computations, guess the value of limx,,[l/(4x - 2)]., We make a table using a calculator and round off to three significant figures:, , It appears that the limit is a number which, when rounded to three decimal, places, is 0.071. In addition, we may notice that as x + 4 , the expression, 4 x - 2 in the denominator of our fraction approaches 14. The decimal, expansion of & is 0.071428 . . . , so we may guess that, , We summarize the idea of limit in the following display., , Copyright 1985 Springer-Verlag. All rights reserved.

Page 11 :
1.2 Limits, , 59, , If the value of f(x) approximates the number I for x close to x,, then we, say that f approaches the limit I as x approaches x,, and we write, f(x)+l, , as x+x,,, , or, , limf(x)=I., , X--fX',, , The following points should be noted., 1. The quantity limx,,o f(x) depends upon the values of f(x) for x near x,,, but not for x equal to x,. Indeed, even if f(x,) is defined, it can be changed, arbitrarily without affecting the value of the limit., 2. As x gets nearer and nearer to x,, the values of f(x) might not approach, any fixed number. In this case, we say that f(x) has no limit as x + x,, or, that lim,,xo f(x) does not exist., , 3. In determining limx,xo f(x), we must consider values of x on both sides of, xo., , 4. Just as in our discussion of the derivative, one can still legitimately, complain that the definition of limit given in the preceding display is too, vague. Readers who wish to see an air-tight definition should now read the, first few pages of Section 11.1. (Section 11.1 is needed for other theoretical, points in Chapter 11 and for proofs, but not for what follows here.), Example 2, , Reading the graph in Fig. 1.2.2, find lim,,,g(t), and 5., , if it exists, for b = 1, 2, 3, 4,, , Figure 1.2.2. Find the, limits of g at the indicated, points. A small circle, means that the indicated, point does not belong to, the graph., , Solution, , Notice first of all that we have introduced new letters; lim,+,g(t) means the, value approached by g(t) as t approaches b., b = 1: lim,+, g(t) = 0.5. In this case, g(b) is defined and happens to be, equal to the limit., b = 2: lim,,,g(t) = 1. In this case, g(b) is defined and equals 1.5, which, is not the same as the limit., b = 3: lim,,,g(t) does not exist. For t near 3, g(t) has values near 0.5, (for t < 3) and near 1 (for t > 3). There is no single number, approached by g(t) as t approaches 3., b = 4: lim,+,g(t) = 1. In this case, g(b) is not defined., b = 5: lim,,,g(t) does not exist. As t approaches 5, g(t) grows larger and, larger and does not approach any limit. A, The computation of limits is aided by certain properties, which we list in the, following display. We will make no attempt to prove them until Chapter 11., Instead, we will present some remarks and graphs which suggest that they are, reasonable., , Copyright 1985 Springer-Verlag. All rights reserved.

Page 12 :
80, , Chapter I Derivatives and Limits, , Assume that limx,xo f(x) and limx,xog(x) exist:, , Constant function rule:, , Identity function rule:, , Replacement rule: If the functions f and g have the same values for all x, near x,, but not necessarily including x = x,, then, , The sum and product rules are based on the following observation: If we, replace the numbers y , and y2 by numbers z , and z2 which are close toy, and, y,, then z , 2, and z ,z, will be close to y , + y2 and y , y2, respectively., Similarly, the reciprocal rule comes from such common sense statements as, "1/14.001 is close to 1/14.", The constant function rule says that if f(x) is identically equal to c, then, f(x) is near c for all x near x,. This is true because c is near c., The identity function rule is true since it merely says that x is near x, if x, is near x,. Illustrations of the constant function rule and the identity function, rule are presented in Fig. 1.2.3., , +, , Fiyre 1.23. In (a), lirn,,,nc, = c and in (b), , Finally, the replacement rule folIows from the fact that Iim,,,of(x), depends only on the values of f(x) for x near x,, and not at x, nor on values, of x far away from x,. The situation is illustrated in Fig. 1.2.4., Example 3, , Use the basic properties of limits: (a) to find lim,,,(x2 + 2x + 5); (b) to show, lim,-,[(2x2 - 7x + 3)/(x - 3)J = 5 as we guessed in the introductory calculation at the start of this section, and (c) to find lim,+,[(8u2 + 2)/(u - I)]., , Copyright 1985 Springer-Verlag. All rights reserved.

Page 13 :
1.2 Limits, , Figure 1.2.4. If the graphs, , 61, , Y, , off and g are identical near, x,, except possibly at the, single point where x = xo,, then lirn,,,o f(x), = lirnx-+xog(x)., Solution, , (a) Common sense suggests that the answer should be 32 + 2 . 3 + 5 = 20. In, fact this is correct., By the product and identity function rules,, lim x2= lim (x . x) =, , x+3, , x-3, , By the product, constant function, and identity function rules,, , By the sum rule,, , Finally, by the sum and constant function rules,, , (b) We cannot use common sense or the quotient rule, since, l i m ( x - 3 ) = limx- l i m 3 = 3 - 3 = 0 ., x+3, , x-3, , x+3, , Since substituting x = 3 into the numerator yields zero, x - 3 must be a, factor; in fact, 2x2 - 7x + 3 = (2x - l)(x - 3), and we have, , For x # 3, we can divide numerator and denominator by x - 3 to obtain, 2x - 1. Now we apply the replacement rule, with, f ( x ) = 2x2 - 7x, and g(x) = 2x - 1, x-3, since these two functions agree for x # 3. Therefore, +, , lim 2 x 2 - 7 x f, = lim(2x- 1 ) = 2, - I = 2 . 3 - 1=5., x -3, x-3, (c) Here the letter "24" is used in place of "x," but we do not need to change, our procedures. By the sum, identity, and constant function rules, we get, lim,,,(u - 1) = limU,,u - lim,,,l = 2 - 1 = 1. Similarly,, x+3, , lim (8u2 + 2), , u-2, , = lim8u2+ lim2, u-2, , u-2, , (sum rule), (product and constant function rules), (product and constant function rules), , =8.2-2+2=34, , (identity function rule)., , Copyright 1985 Springer-Verlag. All rights reserved.

Page 14 :
62, , Chapter 1 Derivatives and Limits, , Thus, by the product and reciprocal rules,, , lim, , u+2, , 8uifZ, = lim, u-1, u-t2, =, , (8u2+ 2) -, , lirn (8 u2 + 2) ., , ~ + 2, , -, , ( U- 1), 1, , I, , =3, , lim (u - 1), , 4 . 1 = 34., 1, , u-+2, , This agrees with the common sense rule obtained by substituting u = 2. g, As you gain experience with limits, you can eliminate some of the steps used, in the solution of Example 3. Moreover, you can use some further rules which, can be derived from the basic properties., , Assume that the limits on the right-hand sides below exist. Then we, Extended sum rule:, , Extended product rule:, , Constant mubiple rule:, , (n, , = 0,, , + I, + 2, + 3, . . . and x, .f 0 if n is not positive)., , We outline how these derived properties can be obtained from the basic, properties. To prove the extended sum rule with three summands from the, basic properties of limits, we must work out lim,,,o( f,(x) f2(x) +f3(x)), when lim,,xoj(x) is known to exist. The idea is to use the basic sum rule for, two summands. In fact fl(x) f2(x) + f3(x) = f 1 ( ~+) g(x), where g(x), = f2(x) + f3(x). Note that lim,,,og(x), = limx-txo, f2(x) + limx,,o f,(x) by the, basic sum rule. Moreover lim,,x~f,(x) + g(x)) = lirnx,,o f,(x) limx,,og(x), by the same rule. Putting these results together, we have, , +, , +, , +, , + hlo g(x), = lirn f,(x) + lim f2(x) + lirn f3(x),, x9xo, = lirn fl(x), x3xo, , x-X,,, , X-JX,,, , as we set out to show. The extended sum rule with more than three terms is, now plausible; it can be proved by induction (see Exercise 65). The extended, , Copyright 1985 Springer-Verlag. All rights reserved.

Page 15 :
1.2 Limits, , 83, , product rule can be proved by very similar arguments. To get the constant, multiple rule, we may start with the basic product rule lim,,,Jf(x)g(x)], = [lim,+,o f(~)][lim,,,~g(x)]. Let g(x) be the constant function g(x) = c;, = [lim,,,,c][lim,+,J(x)], =, the constant function rule gives lim,,,Jcf(x)], c lim,,,o f(x), as we wanted to show. Similarly, the quotient rule follows from, the basic product rule and the reciprocal rule by writing f / g = f - I/g. The, power rule follows from the extended product rule with f,(x) = x, . . . ,, f,(x) = x and the identity function rule. The next example illustrates the use, of the derived properties., Example 4, Solution, , Find lim x 3 - 3x2 + 14x, + I, x 6 + x3+ 2, Common sense correctly suggests that the answer is (13 - 3 . l2 + 14 - 1)/, (16 l 3 + 2) = 3. To get this answer systematically, we shall write f(x) = x3 3x2 14x, g(x) = x6 + x3 2, and use the quotient rule. First of all,, lim,,,x6 = l6 = 1 and limx,,x3 = 1 by the power rule; lim,,,2 = 2 by the, constant function rule; since all three limits exist, lim,,, g(x) = 1 + 1 + 2 = 4, by the extended sum rule. Similarly, lim,,, f(x) = 12. Since limx,, g(x) # 0,, the quotient rule applies and so lim,,,[f(x)/g(x)] = 9 = 3, as we anticipated. A, , +, +, , +, , Clearly the common sense method of just setting x = 1 is far simpler when it, works. A general term to describe those situations where it does work is, "continuity.", , Deflrritron of Continuity, A function f(x) is said to be continuous at x, , = x,, , if lim,,,o, , f(x), , = f(xo)., , Thus if f(x) is continuous at x,, two things are true: (1) limx+,of(x) exists and, (2) this limit can be calculated by merely setting x = x, in f(x), much as in, Example 4. The geometric meaning of continuity will be analyzed extensively, in Section 3.1., We now discuss certain functions which are continuous at many or all, values of x,. Instead of the specific function (x3 - 3x2 14x)/(x6 x3 + 2),, we consider more generally a ratio r(x) = f(x)/g(x) of two polynomials. Such, a ratio is called a rational function, just as a ratio of integers is called a rational, number. Note that a polynomial f(x) is itself a rational function--we can, simply choose the denominator g(x) in the ratio r(x) to be g(x) = 1. Suppose, that we are interested in the rational function r(x) = f(x)/g(x) for values of x, near x,. Moreover, suppose that g(x,) # 0 so that r(x,) is defined; for, instance, in Example 4 we had g(x,) = 4 + 0 at x, = I . Using the limit rules in, almost exactly the same way as we did in Example 4 leads to the conclusion, that the common sense approach works for the rational function r(x). We, summarize in the following box., , +, , +, , Continuity of Rational Functions, If f(x) is a polynomial or a ratio of polynomials and f(x,) is defined,, then, lim f(x) = f(x0)., , x j x o, , Copyright 1985 Springer-Verlag. All rights reserved.

Page 16 :
64, , Chapter 1 Derivatives and Limits, , As an example of the use of the continuity of rational functions, note that, to calculate limX,,[l/(4x - 2 ) ] , we can now just set x = 4 to get &, as we, guessed in Example 1 above. Indeed, students seduced by the simplicity of this, rule often believe that a limit is nothing more than a value. The next example, should help you avoid this trap., Example 5, , Find, , and, (b), , lim, Ax-+o, , + 2 Ax, AX)^ + Ax, , ', , where Ax is a variable., Solution, , (a) The denominator vanishes when x = 2, so we cannot use the continuity of, rational functions as yet. Instead we factor. When the denominator is not zero, we have, , Thus, x+3, lim x2 + x - 6 =, x-2 X + 4, x2 + 2 X - g, , (by the replacement rule), , x-2, , ---- +, , 2+4, , (by the continuity of rational functions)., , 6, , (b) The denominator vanishes when Ax = 0, so again we use the replacement, rule:, + 2 Ax, lim, = lim A X - (replacement rule), Ax40, + Ax Ax-0 AX + 1, +, , =2, , (continuity of rational functions). A, , There are many limits that cannot be dealt with by the laws of limits we have, so far. For example, we claim that if x , is positive, then, lim, , x+x0, , G=&,, , i.e., the function f(x) = & is continuous at x,. To make this result plausible,, assume that l i m X j x o ~= I exists. Then by the product rule,, , Now I must be positive since & > 0 for all x which are positive, and all x, which are close enough to x , are positive. Hence, I =&. This limit is, consistent with the appearance of the graph of y =, (See Fig. 1.2.5.), In Section 11.1, we give a careful proof of the continuity of, , 6., , 6., , Copyright 1985 Springer-Verlag. All rights reserved.

Page 17 :
1.2 Limits, , Figure 1.2.5. The graph of, y = 6 suggests that, lirnx++,6 = 6 ., , 65, , J., , Example 6, , Find, 8x2 ., lim ----x - 9 3 1 +6, By using the properties of limits and the continuity of &, we get, lim,,,(l, i-6) = lim,,,l, + lim,,,& = 1 +& # 0. Thus, , Solution, , lim 8x2, 8x2 =, x+3, lim ---x-3, 1 + 6, lim(l+&), x-3, , - 8 .3*, -, , 1i-\15, , =, , 72, , I+-\15, , .A, , Sometimes limits can fail to exist even when a function is given by a simple, formula; the following is a case in point., Does lim,,,(l, , Example 7, , Solullon, , x l/x) exist?, , The function in question has the value 1 for x > 0 and - 1 for x < 0. For, x = 0, it is undefined. (See Fig. 1.2.6.)-There is no number 1 which is, , Figure 1.2.6. The graph of, the function Ixl/x., , approximated by Ixl/x as x +O, since Ixl/x is sometimes 1 and sometimes, - 1, according to the sign of x. We conclude that lim,,,(lx)/x), does not exist., , A, It is possible to define a notion of one-sided limit so that a function like Ixl/x, has limits from the left and right (see Section 11.1 for details). Since the, one-sided limits are different, the lirnit per se does not exist. The reader might, wonder if any function of interest in applications actually shows a jump, similar to that in Fig. 1.2.6. The answer is "yes." For example, suppose that a, ball is dropped and, at t = 0, bounces off a hard floor. Its velocity will change, very rapidly from negative (that is, downward) to positive (that is, upward). It, is often convenient to idealize this situation by saying that the velocity, function jumps from a negative to a positive value exactly at t = 0, much as in, Fig. 1.2.6., We conclude this section with some limits involving + oo. We shall be, quite informal and emphasize examples, again leaving a more careful discussion to Chapter 1 1 . First, it is often useful to consider limits of the form, lim,,,, j(x). This symbol refers to the value approached by j(x) as x becomes, arbitrarily large. Likewise, lim,,-,, f(x) is the value approached by f(x) as x, gets large in the negative sense. Limits as x -+ + oo obey similar rules to those, with x -+ x,., , Copyright 1985 Springer-Verlag. All rights reserved.

Page 18 :
66, , Chapter 1 Derivatives and Limits, , Example 8, , Find, ("), , 1 ;, lim -, , x i m X, , 2x+1., lim ---3x 1 ', , (b), , +, , x+m, , and, , Solution, , As x gets very large, 1/x gets very small. Thus, 1 = 0., lim (a) x + m X, We shall do (b) and (c) by writing the given expression in terms of l / x ., 2 x + ' = lim --Iim --3~ 1 X-)m 3 + I / x, , (b), , Example 9, , +, , x+m, , Find lim,-,,, , f(x) and Iim,,, , _, , ,, f(x), , 3 +O, , 3 ', , for the function f in Figure I .2.7., , Figure 1.2.7. Find, lim,,,, f ( x ) and, lim,+ - ,, f(x)., , Solution, , Assuming that the ends of the graph continue as they appear to be going, we, conclude that lim,,,, f(x) = 2 and limx,_, f(x) = 0. A, Another kind of limit occurs when the value of f(x) becomes arbitrarily large, and positive as x approaches x,. We then write lim,,xo f(x) = oo. In this case, limx+xof(x) does not, strictiy speaking, exist (infinity is not a real number)., SimilarIy lim,,,of(x) = - w is read "the limit of f(x) as x approaches x, is, minus infinity," which means that while lim,,,,, f(x) does not exist, as x, approaches x, from either side f(x) becomes arbitrarily large in the negative, sense., , Example 10, , Find, (a), , lim, , x+2, , - 3x, x2 - 4x + 4, , and, (b), Solution, , 3x+2 ., 1im -, , x+o, , X, , (a) The denominator vanishes when x = 2, so the quotient rule does not apply., We may factor the denominator to get - 3x/(x2 - 4x 4) = - 3x/(x - 212., , +, , Copyright 1985 Springer-Verlag. All rights reserved.

Page 19 :
1.2 Limits, , 67, , For x near 2, the numerator is near - 6 , while the denominator is small and, positive, so the quotient is large and negative. Thus,, lim, x-2, , -3x, =-m., ( x - 212, , (See Fig. 1.2.8(a).), (b) We write (3x 2)/x = 3 2/x. When x is near 0, 2/x is either large and, positive or large and negative, according to the sign of x (Fig. 1.2.8(b)). Hence, limx,0[(3x + 2)/x] does not have any value, finite or infinite. (To get + oo or, - oo, one-sided limits must be used.) A, , +, , +, , Figure 1.2.8. In (a) the limit, is - oo and in (b)it does, not exist., lim, x-2, , - 3x, x2- 4x, , + 4 =-co, , Exercises for Section 1.2, 1. Guess lim,+,[(x3 - 3 x 2 + 5 x 3 ) / ( x, , - I)] by, doing numerical calculations. Verify your guess, by using the properties of limits., 2. Find limx,_ , [ 2 x / ( 4 x 2 + 5)], first by numerical, calculation and guesswork, then by the basic, properties of limits, and finally by the continuity, of rational functions., Refer to Fig. 1.2.9 for Exercises 3 and 4., 3. Find lim,,-3 f ( x ) and lim, f ( x ) if they exist., 4. Find lim,,-, f ( x ) and lim,,, f ( x ) if they exist., , +,, , 3x, , y, , +, , =, , x, , is infinitely schizophrenic near x, , =0, , Use the basic properties of limits to find the limits in, Exercises 5-8., 6. lim x 2, 5. lim (17 + x ), x+3, , x+3, , u+ l, 7. lirn u+-1, u-1, , s2- 1, 8. lirn s+2, , S, , Use the basic and derived properties of limits to find, the limits in Exercises 9-12., x2- 9, , 9. lirn x+3 x 2 + 3, 10. lirn, x, , 2, , 11. lim, , + 3 x - 10), ( x + 2), xI0 + 8 x 3 - 7 x 2 - 2, (x2, , x + !, , x +I, , 12. lim, x-2, , (x2, , + 3x - 9), x +2, , Use the continuity of rational functions and the replacement rule, if necessary, to evaluate the limits in, Exercises 13-22., u--0, t-Js, 14. lirn 13. lirn ,+&, t2- 5, .+A u2 - 3, x, 2-3, x -2, 16. lirn 15. lirn x+3 x 2 - 3, x+2 X - 2, Figure 1.2.9. Find the limits at x = - 3 , - 1, 1, and 3 if, they exist. A small circle means that the indicated point, does not belong to the graph., , 17. lirn, x+3, , 19. lim, Ax+0, , x2 - 4x, x 2 - 2x, , +3, , 3, + 3(Ax), -, , AX, , lim, x+-5, , 20. lim, Ax-0, , +, , x 2 x - 20, x2+6x+ 5, (AX)', AX)^, , +, , AX, , Copyright 1985 Springer-Verlag. All rights reserved.

Page 20 :
68, , Chapter IDerivatives and Limits, , 21. lirn, Ax+O, , 22. lirn, , AX)' +, , Refer to Fig. 1.2.12 for Exercises 39 and 40 (assume, that the functions keep going as they appear to)., f(x) and limx,_, f(x)., 39. Find lim,,,, 40. Find lim,,,, g(x) and lim,,-,, g(x)., , AX), , Ax, , AX)^ + AX)' +, , A AX), , Ax-0, AX, Find the limits in Exercises 23-26 using the continuity, of 6 ., 2x2 - X, 2x, 24. lirn 23. lim x-9, x+4 1 - 6, 6, , 25. limx,3(1 - &)(2 + 6 ) 26. limx,2(x2 + 2 x ) a, Find the limits in Exercises 27-30 if they exist. Justify, your answer., , Ix - 11, Ix - 21, 29. lirn 30. lirn x-tl X - 1, x+2 x - 2, Find the limits in Exercises 3 1-36 as x + -t oo., 2x2 1, x-1, 32. lim 31. lirn x + m 2x + 1, x + m 3x2 2, 3x3 + 2x2 1, 34. X +lim, 33. x!jmm 2x - m 4x3 - x 2 + X + 2, 1x1, X, 35. lim 36. lim x-+m x, x-t-m, 1x1, 37. For the function in Fig. 1.2.10, find lim,,,f(x), for a = 0, 1,2,3,4 if it exists. In each case, tell, whether lim,,, f(x) = f(a)., , +, +, , +, , Figure 1.2.12. Find the, limits at t oo., Find the limits in Exercises 41-44. If the limit is, give that as your answer., Y-4, 42. lim, Y-3 y 2 - 6y + 9, 2, 43. lim 44. lim x 2 5x, x+6x 2 - 5, x-to, x2, Find the limits in Exercises 45-58 if they exist., u3 + 2u2 + U, 45. lim, u-to, u, x, 3, +, 2, 46. lim X + m 3x3 + X, 2x, 47. lirn x+2 ( x - 2)2, , + oo,, , +, , 49. lim x 2 - 5x + 6, x+2 x 2 - 6x + 8, 50. lim x 2 - 5x + 6, x+4 x 2 - 6x + 8, t2 2 4, 51. lim -, , +, , F i w e 1.2.10. Find the, limits at 0, 1,2,3,4., , t+4, , It(, , 38. Find lim,,,f(x),, where a = -2, 0, and 1 for f, sketched in Fig. 1.2.1 1., , 54. lirn, , (Ax14, , + 2 AX)^ + 2 Ax, AX, , dx+O, , 3(x3 - 1), 55. lim, x+l, X-1, 56. lirn, q+3, , 57. lirn 3s2 - 2s - 21, s-3, ( s - 3)2, , Figure 1.2.11. Find, limx,,f(x) at the indicated, points., , 58., , lim, , x+-00, , fi, , -, , x2+ 1, , 59. How should f(x) = (xS - I)/(x - I ) be defined, at x = 1 in order that lim,,, f(x) = f(l)?, , Copyright 1985 Springer-Verlag. All rights reserved.

Page 21 :
1.3 The Derivative as a Limit and the Leibniz Notation, 60. I-Iow should g ( t ) = (t2 + 4t)/(t2 - 4t) be defined, at t = 0 to make lim,,,g(t) = g(O)?, a61. A block of ice melts in a room held at 75OF. Let, f(t) be the base area of the block and g(t) the, height of the block, measured with a ruler at, time t ., (a) Assume that the block of ice melts completely at time T. What values would you, assign to f ( T ) and g(T)?, (b) Give physical reasons why lim,,,f(t), =, f ( T ) and lim,,,g(t) = g ( T ) need not both, hold. What are the limits?, (c) The limiting volume of the ice block at time, T is zero. Write this statement as a limit, formula., (d) Using (b) and (c), illustrate the product rule, for limits., s62. A thermometer is stationed at x centimeters from, a candle flame. Let f(x) be the Celsius scale, reading on the thermometer. Assume that the, glass in the thermometer will crack upon contact, with the flame., (a) Explain physically why f(O) doesn't make, any sense., (b) Describe in terms of the thermometer scale, the meaning of lim,,o+ f(x) (i.e., the limit, of f(x) as x approaches zero through positive values)., (c) Draw a realistic graph of f ( x ) for a scale, with maximum value 200°C. (Assume that, the flame temperature is 400°C.), , s63., , k64., , +65., , 69, , (d) Repeat (c) for a maximum scale value of, 500°C., Suppose that f(x) # 0 for all x # xo and that, lim,,,o f ( x ) = oo. C a n you conclude that, lim,,,O[l /f(x)] = O? Explain., Draw a figure, similar to Figs. 1.2.3 and 1.2.4,, which illustrates the sum rule in our box on basic, properties of limits., (a) Prove the extended sum rule in the box on, derived properties of limits for the case, n = 4 by using the basic sum rule and using, the extended sum rule for the case n = 3, proved in the text., (b) Assume that the extended sum rule holds, when n = 16; prove from your assumption, that it holds when n = 17., (c) Assume that the extended sum rule holds for, some given integer n > 2; prove that it holds, for the integer n + 1., (d) According to the principle of induction, if a, statement is true for n 1 whenever it is, true for n, and is true for some specific, integer, m, then the statement is also true for, rn + 1, m + 2,m + 3, . . . , i.e., it is true for, aii integers larger than m. Use induction and, the basic sum rule to prove the extended, sum rule., Prove the extended product rule for limits by, induction (see Exercise 65) and the basic properties of limits., , +, , *66., , 1.3 The Derivative as a Limit, and the Leibnlz Notation, The derivative is the limit o j a difSerence quotienl, , We are now ready to tie together the discussion of the derivative in Section 1.1, with the discussion of limits in Section 1.2., Let f ( x ) be a function such as the one graphed in Fig. 1.3.1. Recall the, following items from Section 11.1: If ( x , , f(xo)) and ( x , + Ax, f ( x o A x ) ) are, two points on the graph, we write Ay = f(xo + A x ) - f(x,) and call A y / A x the, , +, , t, , /, , Slope = f " ( x o ), , Figure 1.3.1. The limit of, Ay/Ax as Ax -+ 0 isf(xo)., , Copyright 1985 Springer-Verlag. All rights reserved.

Page 22 :
70, , Chapter 1 Derivatives and Limits, , difference quotient. This difference quotient is the slope of a secant line, as, shown in the figure; moreover, if f(x) is distance as a function of time, then, Ay/Ax is an average velocity. If Ax is small, then Ay/Ax approximates the, derivative f'(xo). Using these ideas, we were led to conclude that f'(xo) is the, slope of the tangent line; moreover if f(x) represents distance as a function of, time, f'(x,) is the instantaneous velocity at time x,. We can now make our, discussion of f'(x,) more precise using the language of limits., Suppose that the domain of a function f(x) contains an open interval, about a given number x,. (For example, we might have x, = 3, and f(x) might, be defined for all x which obey I < x < 4.) Consider the difference quotient, , as a function of the variable Ax. The domain of the difference quotient then, consists of those Ax, positive or negative, which are near enough to zero so, that f(x, + Ax) is defined. Since Ax appears in the denominator, Ax = O is not, in the domain of the difference quotient. (For instance, in the example just, mentioned with x, = 3 and 1 < x < 4, Ay/Ax would be defined for -2 < Ax, < 0 and O < Ax < I.) As the examples in Section 1.1 indicated, we should, look at the limit of Ay/Ax as Ax + O . This leads to the following definition of, the derivative in terms of limits., , Let f(x) be a function whose domain contains an open interval about x,., We say that f is differentiable at x, when the following limit exists:, , f'(x,) is then called the derivative of f(x) at x,., , Example 1, , Solullon, , Suppose that f(x) = x2. Then f'(3) = 6 by the quadratic function rule with, a = 1, b = O = c and x, -. 3. Justify that f'(3) = 6 directly from the formal, definition of the derivative and the rules for limits., We write the difference quotient and simplify:, -=, , f(x,, , + Ax) - f(x,), , 6Ax +, - (3 + Ax)' - 3', -, , Ax, Ax, Ax, Ax, The independent variable is now Ax, but, of course, we can still use the rules, for limits given in the previous section. By the replacement rule, we can, cancel:, 6 Ax, , +, , = lim (6 + Ax),, AX, Ax+O, provided the latter limit exists. However, 6 + Ax is a polynomial in the, variable Ax and is defined at Ax = 0, so by the continuity of rational, functions, limA,,,(6 + Ax) = 6 + O = 6. A, , lim, , Ax+O, , Example 2, , Use the formal definition of the derivative and the rules for limits to differentiate x3., , Copyright 1985 Springer-Verlag. All rights reserved.

Page 23 :
1.3 The Derivative as a Limit and the Leibniz Notation, , Solution, , Lettingf(x), , = x3, we, , Y(xo) =, , have, , ~ ( X+OAx) - f(xo), ~~~,, Ax, , = lim, , xi, , lim, , lim, Ax+,, , + AX)^ - x i, Ax, (expanding the cube), , Ax, 3x:Ax, , + 3x,(Ax)* +, Ax, , Ax+,, , =, , (x,, =, , + 3x02 A X + 3x0(AX)*+ AX)^ - x i, , Ax+O, , =, , 71, , lim (3x02 + 3x,Ax, , Ax+,, , + AX)^), , (by the replacement rule), , (using the continuity of rational functions and setting Ax, The derivative of x3 at x, is therefore 3x;. A, , = 0)., , As the next example shows, we can write x instead of x, when differentiating, by the limit method, as long as we remember that x is to be held constant, when we let Ax +0., Example 3, Solullon, , If f(x) = I/x, find f ( x ) for x # 0., The difference quotient is, , ay--, , a/(x, , Ax, , + AX)- I / X, Ax, , -, , x - ( X + AX), Ax, = x(x + AX)AX, x (x + Ax) Ax, , Here x is being held constant at some nonzero value, and Ay/Ax is, considered as a function of Ax. Note that Ax is in the domain of the, difference quotient provided that Ax # 0 and Ax # -x., For Ax # 0, A y/Ax equals - l/x(x Ax), so, by the replacement rule,, , +, , - - -1, , x, , (by the continuity of rational functions)., , Thus, f'(x) = - 1/x2. A, If we look back over the examples we have done, we may see a pattern. The, derivative of x3 is 3x2 by Example 2. The derivative of x2 is given by the, quadratic function rule as 2x' = 2x. The derivative of x x ' is 1 . xo = 1 ,, and the derivative of 1/ x = x - is ( - 1 ) ~ by, - ~Example 3. In each case,, when we differentiate xn, we get nxn-'. This general rule makes it unnecessary to memorize individual cases. In the next section, we will prove the rule, for n a positive integer, and eventually we will prove it for all numbers n. For, now, let us see how to prove the rule for x'12 = fi.We should get + x ( ' / ~ ) - ', = ix-'/2 = 1 / 2 6 ., , ', , Example 4, , Solullon, , Differentiate, , -, , 6 (x > 0)., , The difference quotient is, , Copyright 1985 Springer-Verlag. All rights reserved.

Page 24 :
72, , Chapter I Derivatives and Limits, , In order to cancel Ax, we perform a trick: rationalize by multiplying numerator and denominator by I/=, + 6:, , (x, , -, , + Ax) - x, , -, , ~x(Jxax+G), , 1, , JX+6, , Notice that this trick enabled us to cancel Ax in the numerator and, denominator., Now recall from the previous section that limx,xofi =&. Thus,, lim,,,,{~, = 6.Hence, by the quotient rule for limits,, , AY =, lim Ax, lim, , AX-0, , Ax+O, , 1, , + 6), , ({=, , (sum rule), , 1, , -, , + Ax+O, lim 6, , lim, , Ax-0, , -, , 1, , =-, , 6+6, , 1, , (continuity of 6 ) ., , 2 6, , Thus, the derivative is indeed 1 / 2 6 . A, Next, let us establish a general relationship between differentiability and, continuity., , Proof, , We first note that lim,,xo f(x) = f(xO)is the same as lim,,,n( f(x) - f(xo)) = 0, (by the sum rule and then the constant function rule applied to the constant, f(xo)). With Ax = x - xo, and Ay = f(xo + Ax) - f(xo), this is, in turn, the, same as limA,,oAy = 0. Now we use again the trick of multiplying numerator, and denominator by an appropriate factor:, , lim ~, , y lim, = (&.ax), , Ax+O, , Ax-0, , =, , AX, , (replacement rule), , ', , (product rule), ( )!mo g)(dirqo, Ax), lim, (since Ax-+,, , Ax = 0, , = 0., This proves our claim. adll, , The converse theorem is not true; the following is a counterexample., Example 5, , Show that f(x) = 1x1 has no derivative at x,, Section R.2 for a review of absolute values.), , = 0,, , yet is continuous. (See, , Copyright 1985 Springer-Verlag. All rights reserved.

Page 25 :
1.3 The Derivative as a Limit and the Leibniz Notation, , Solullon, , F i p e 13.2. As x 3 0 from, either direction, 1x1 +0, so, f(x) = 1x1 is continuous at 0., , 73, , The difference quotient at x, = 0 is (10 + Ax1 - lQl)/Ax = lAxl/Bx, which is 1, for Ax > 0 and - 1 for Ax < 0. As we saw in Example 7 of Section 1.2, the, function lbxl/Ax has no limit at Ax = 0, so the derivative of 1x1 at x, = 0 does, not exist., , (x,, , Ixi), , =, , --, , On the other hand, as x+O, f(x), lim,,,lxl, = 101; 1x1 is continuous at 0. A, , =:, , lxl-+0 as well (see Fig. 1.3.21, so, , We have seen that the derivative f'(x,) of y = f(x) at x, is approximated by, the difference quotient Ay/Ax, where Ax = x - x,., In the view of Gottfried WilheIm von Leibniz (1646-17161, one of the, founders of calculus, one could think of Ax as becoming "infinitesimal." The, resulting quantity he denoted as dx, the letters d and A being the Roman and, Greek equivalents of one another. When Ax became the infinitesimal dx, Ay, simultaneously became the infinitesimal dy and the ratio Ay/Ax became, dy/dx, which was no longer an approximation to the derivative but exactly, equal to it. The notation dy/dx has proved to be extremely convenient-not, as a ratio of infinitesimal quantities but as a synonym for f ' ( ~ ) . ~, , If y = f(x), the derivative f'(x) may be written, , This is just a notation and does not represent division. If we wish to, denote the value f'(x,) off' at a specific point x,, we may write, , dy/dx is read "the derivative of y with respect to x" or "dy by dx.", , Of course, we can use this notation if the variables are named other than x, and y. For instance, the area A of a square of side 1 is A = l 2 SO we can write, dA/d1= 21., In the f' notation, if f(x) = 3x2 + 2x, then f'(x) = 6x + 2. 'Using the, Leibniz notation we may write:, d~ = 6x + 2., then if y = 3x2 + 2x,, dx, Modern developments in mathematics have made it possible to give rigorous definitions of dx, and dy. The earlier objections to infinitesimals as quantities which were supposed to be smaller, than any real number but still nonzero have been circumvented through the work of the logician, Abraham Robinson (1918-1974). A calculus textbook based upon this approach is H. J. Keisler,, Elementary Calculus, Prindle, Weber, and Schmidt, Boston (1976)., , Copyright 1985 Springer-Verlag. All rights reserved.

Page 26 :
74, , Chapter 1 Derivatives and Limits, , We can also use the even more compact notation, , Here the d/dx may be thought of as a symbol for the operation of differentiation. It takes the place of the prime (') in the functional notation., Example 6, , Solution, , (a) Find the slope rn of the graph y, bus whose distance function is t3., , =, , 6 at x = 4. (b) Find the velocity v of a, , (a) The slope is a derivative. The derivative of 6 is dy/dx = d(&)/dx, = 1/(2\/;r) by Example 4. Evaluating at x = 4 gives rn = 1/(2@) =, (b) v = (d/dt)(t3) = 3t2. A, , a., , Supplement to Section 1.3, Filling a Pond, We conclude this section with a harder and perhaps more interesting application that previews some important topics to be considered in detail later: rates, of change (Section 2.1) and integration (Chapter 4)., Suppose that a mountain brook swells from a trickle to a torrent each, year as the snows melt. At the time t (days after midnight on March 31), the, flow rate is known to be 3t2 thousand liters per day. We wish to build a large, pond which holds the runoff for the entire month of April. How big must the, pond be?, The main difficulty here is that a flow rate of, say 3 . (5)' at midnight of, April 5 does not tell us directly how much water will be in the pond on April, 5, but merely how fast water will be pouring in at that moment. Let's see if we, can somehow handle that difficulty., Designate the unknown amount of water in the pond at time t by, A = f(t). During a short time interval At starting at t, the amount of water, ~., entering the pond will be at least 3t2At and no more than 3(t A E ) ~ AThus,, AA = A(t At) - A(t) is slightly larger than 3t2 At. For At very small, we, can presumably take AA w3t2At, i.e., AA/At w3t2. However, for At very, small, AA /At approximates the derivative dA / dt. Thus our problem becomes, the following. Find the "amount" function f(t), given that the derivative obeys, f ( t ) = 3t2., Now, turning Example 2 around, we know one function which obeys, f ( t ) = 3t2, namely f(t) = t3. This solution is reasonable in the sense that, f(0) = 0,i.e., the pond is empty at midnight of March 31. Could there also be, a different amount function that works? Not really. If a capacity of t 3, thousand liters is exactly right to accommodate all the influx up to time t , no, other capacity will be exactly right. We thus have our answer: at midnight on, April 30, A = f(30) = (30)3; our pond must hold 27,000 thousand liters., , +, , +, , Exercises for Section 1.3, Use the formal definition of the derivative and the rules, for limits to find the derivatives of the functions in, Exercises 1- 12., 1. f(x)=x2+x, , Copyright 1985 Springer-Verlag. All rights reserved.

Page 27 :
1.4 Differentiating Polynomials, , Show that the functions in Exercises 13 and 14 have no, derivative at xo, yet are continuous., 13. f ( x ) = 1 + 1x1; x0 = 0, 14. g ( x ) = Ix 11; xo = - 1., Find dy/dx in the Exercises 15-18., 16. y = x - 5x2, 15. y = x 2 - x, 17. y = 3x3 + x, 18. y = x2 - x 3, In Exercises 19 and 20, find the slope o f the line, tangent to the given graph at the given point., 19. y = 8 & ; x o = 9, 20. y = 2 x 2 - J ; ; + l / x ; x o = 1, In Exercises 21 and 22, f ( t ) is the position o f a car on a, straight road at time t. Find its velocity at the given, time., 22. f ( t ) = t 2 - t3; t = 4, 21. f ( t ) = 5t3; t = 1, In Exercises 23-26, evaluate the derivatives., , 75, , ( b ) Show from the rules for limits that i f f ( x ), and g ( x ) are differentiablefunctions, then, , +, , 27. Using the'-hiit method, find the derivative of, I, 2 ~ +3 ~ 2 3- at xo= I ., 28. (a) Expand ( a + b14. ( b ) Use the limit method to, differentiate x4., Use limits to find the derivatives o f the functions in, Exercises 29-32., 29. f ( x ) = 1 / x 2, 30. 3fi, 31. f ( x ) = ( x 2+ x ) / ~ x 32. f ( x ) = x / ( l + x2), *33. Find an example o f a function which is continuous everywhere and which is differentiableeverywhere except at two points., +34. (a) Show by the quadratic function rule that i f, f ( x ) = ax2 + bx + c , g ( x ) = dx2 + ex + f ,, and h ( x ) = f ( x ) + g ( x ) , then h f ( x )=, f ' ( x ) + g r ( x ) ; i.e., ( d / d x ) [ f ( x ) + g ( x ) l, = ( d / d x ) f ( x ) + ( d / d x ) g(x)., , and, , ( c ) Argue geometrically, using graphs and, slopes, that a function C ( x )for which C ' ( x ), = 0 must be a constant function., ( d ) Combining (b) and (c), show that if f'(x), = g l ( x ) , then there is some constant C such, that f ( x ) = g ( x ) + C. Illustrate your result, graphically., (e) In (d) show that i f f(0) = 0 = g(O), then f ( x ), = g ( x ) for all x., ( f ) Use (e) to argue that in the pond example, discussed in the Supplement, A ( t ) = r3 is the, only appropriate solution o f A1(t)= 3t2., *35. (a) Do some calculator experiments to guess, limx,o(sin x / x ) and limx,o[(l - cos x ) / x ] ,, where the angle x is measured in radians., ( b ) Given the facts that limx,o(sinx/x) = 1 and, lim,,o[(l - c o s x ) / x ]= 0, use trigonometric, identities to show:, d(sin x ), dx, , = cos X,, , *36. Suppose that the mountain brook in the Supplement has a flow rate o f t2/12 2t thousand, liters per day t days after midnight on March 3 1 ., What is the runoff for the first 15 days o f April?, The entire month?, , +, , 1.4 Differentiating, Polynomials, Polynomials can be dflerentiated using the power rule, the sum rule, and the, constant multiple rule., , In Section 1.3, we learned how to compute derivatives of some simple, functions using limits. Now we shall use the limit method to find a general, rule for differentiating polynomials like f(x) = 3x5 - 8x4 4x + 2. To do this, systematically, we shall break apart a polynomial using two basic operations., First, we recognize that a polynomial is a sum of monomials: for, example, f(x) = 3 x 5 - 8x4 + 4 x + 2 is the sum of 3x5, - 8x4, 4 x and 2., Second, a monomial is a product of a constant and a power of x. For, example, 3 x 5 is the product of 3 and x5., , +, , Copyright 1985 Springer-Verlag. All rights reserved.

Page 28 :
78, , Chapter 1 Derivatives and Limits, , Let us work backward, starting with powers of x. Thus our first goal is to, differentiate x", where n is a positive integer. We have already seen that for, n = 1,2, or 3 (as well as n = - 1 or +), the derivative of x" is nxn-'., We can establish this rule for any positive integer n by using limits. Let, f(x) = x". To compute f'(x), we must find the limit, lim, , f (X + Ax) - f (x), , AX, Now f(x) = (x + Ax)" = (X + Ax)(x + Ax) . . . (x + Ax), n times. To expand, a product like this, we select one term from each factor, multiply these n, terms, and then add all such products. For example,, Ax+O, , (X + Ax)(x + Ax) = x2 + x AX, (X + Ax)(x + Ax)(x + Ax) = x3 + X, , + (Ax)x +, , + x (Ax)x -t ( A X ) X+~( 8 x 1 ~ ~, + (Ax) x (Ax) + AX)^, , ~ A X, , +x, , For (x + Ax)", notice that the coefficient of Ax will be nxn-' since there will, be exactly n terms which contain n - 1 factors of x and one of Ax. Thus, , (x, , + AX)"=x" + n x n 'Ax + (terms involving (AX)', AX)^, . . . , (Ax)")., , If you are familiar with the binomial theorem, you will know the remaining, terms; however, their exact form is not needed here. For Ax f 0, dividing out, Ax now gives, , -, , nxn-' Ax, , + (terms involving AX)^, . . . , (Ax)"), Ax, , = nx "-, , ' + (terms involving (Ax), . . . , (Ax)"-, , I)., , The terms involving Ax, . . . , (Ax)"-' add up to a polynomial in Ax, so the, limit as Ax -+O is obtained by setting Ax = 0 and by using the 'continuity of, rational functions (Section 1.2). Therefore,, , To differentiate a power x", bring down the exponent as a factor and, then reduce the exponent by 1., If f(x) = x", then f'(x) = nxn- that is, , ';, , -(x") = nxn-I,, , n = 1,2,3, . . . ., , Example I Compute the derivatives of x8, xk2,and x99., Solutlon, , (d/dx)x8 = 8x7, (d/dx)xt2 = 12x", and ( d / d ~ ) x, =~, 9 ~9 ~ A~ ~ ., Next, we consider the constant multiple rule, stated in the following box., , Copyright 1985 Springer-Verlag. All rights reserved.

Page 29 :
4 -4Differentiating Polynomials, , 79, , T o differentiate the product of a number k with f ( x ) , multiply the, number k by the derivative j"'(x):, ( k S ) ' ( x )= kS'(x),, , Proof of the, Constant, Multiple Rule, , Example 2, , Let h ( x )= k f ( x ) . By the definition of the derivative and the basic properties, of limits, we get, h ( x A X )- h ( x ), h l ( x )= lim, Ax+O, AX, kf ( x + A x ) - kf ( x ) = lim k ( f ( +~A X ) f ( x ), = lim, A.x-0, Ax, Ax-0, AX, , +, , Differentiate, (a), , Solution, , (b) 5 6, , -3x7, , (c), , 8, , and, , X, , (d), , -6ax2., , (a) By the constant multiple and power rules,, -d( - 3 x 7 ), dx, , = ( - 3 ) - xd7, , dx, , = ( - 3 ) ( 7 ) x 6=, , ( b ) From Example 4, Section 1.3, ( d / d x ) &, multiple rule,, , =, , -21x6, , 1/2&., , Thus, by the constant, , (c) By Example 3, Section 1.3, ( d / d x )( I / x ) = - 1 / x 2 . Thus, , (d) Although it is not explicitly stated, we assume that a is constant (letters, from the beginning of the alphabet are often used for constants). Thus, by, the constant multiple rule, , The final basic technique we need is the sum rule., If f and g are two functions, the sum f + g is defined by the formula, ( f + g>(x)= f ( x ) + g(x)., Example 3, , Let f ( x ) = 3x2 + 5x + 9 and g ( x ) = 2x2 + 5x. Use the quadratic function rule, g'., to verify that ( f g)' = f ', , Solution, , By the quadratic function rule, f ' ( x ) = 6x 5 and g'(x) = 4 x 5 , thus, f ' ( x ) g'(x) = 10x 10. On the other hand, f ( x ) g ( x ) = 5x2 lox 9, so, (f + g)'(x)= lox + 10 = f ' ( x ) + gl(x). A, , +, , +, , +, , +, , +, , +, , +, , +, , +, , Copyright 1985 Springer-Verlag. All rights reserved.

Page 30 :
78, , Chapter 1 Derivatives and Limits, , To differentiate a sum, take the sum of the derivatives:, , To be convinced that a mathematical statement such as the sum rule is true,, one should ideally do three things:, , I. Check some simple examples directly., 2. Have a mathematical justification (proof)., 3. Have a simple physical model, application, or diagram that makes the, result plausible., In Example 3 we checked the sum rule in a simple case. In the next paragraph, we give a mathematical justification for the sum rule. In the Supplement at the, end of the section, we give a simple physical model., Proof of the, Sum Rule, , By the definition of the derivative as a limit, ( f, lim, , ( f + gX.0, , + Ax> -, , + g)'(xo)is equal to, , ( f + g)(xo), , Ax40, Ax, (if this limit exists). We can rewrite the limit as, , lim, , Ax-0, , f(x0 + Ax) + g(x0 + a x >-f(xo> - g(xo>, AX, f(x0 + Ax) - f(x0), g(xo + Ax) - g(xo>, - +, = lim, Ax+O, Ax, , By the sum rule for limits, this is, lim, , Ax+O, , f(x0 + Ax) - f(x0), AX, , +, , Ax-0, , g(xo + Ax) - g(x0), AX, , I f f and g are differentiable at x,, these two limits are just f'(x,) and gf(x0)., Thus f + g is differentiable at xo, and (f + g)'(xo)= j-'(xo) + g1(x0)., The sum rule extends to several summands. For example, to find a formula, for the derivative of f ( x ) + g ( x ) + h(x), we apply the sum rule twice:, , Example 4, Solution, , Find the formula for the derivative 8 f ( x )- lOg(x)., We use the sum and constant multiple rules:, , Copyright 1985 Springer-Verlag. All rights reserved.

Page 32 :
80, , Chapter I Derivatives and Limits, , The differentiation rules we have learned can be applied to the problems of, finding slopes and velocities., (a) Find the slope of the tangent line to the graph of, , Example 8, , (b) A train has position x, train at t = 2., Solution, , = 3t2, , + 2 - fi at time t . Find the velocity of, , (a) The slope is the derivative at x, , =, , the, , 1. The derivative is, , + 1) = 4x3 - 6x2., dx, 1, this is 4 . l 3 - 6 - l 2 = -2, the required slope., , dy = d (x4 - 2x3, dx, , At x, , =, , (b) The velocity is, , At t = 2, we get, , Supplement ts Section 1.41, A Physical Model lor the Sum Rule, Imagine a train, on a straight track, whose distance at time x from a fixed, reference point on the ground is f(x). There is a runner on the train whose, distance from a reference point on the train is g(x). Then the distance of the, runner from the fixed reference point on the ground is f(x) g(x). (See Fig., 1.4.1.) Suppose that, at a certain time x,, the runner is going at 20 kilometers, , +, , Figure 1.4.1. The sum rule, illustrated in terms of, velocities., , per hour with respect to the train while the train is going at 140 kilometers per, hour-that is, f'(x,) = 140 and g'(x,) = 20. What is the velocity of the runner, as seen from an observer on the ground? It is the sum of 140 and 20-that is,, 160 kilometers per hour. Considered as the sum of two velocities, the number, gt(x0); considered as the velocity of the runner with respect to, 160 is f'(x,), gf(x0), the ground, the number 160 is (f g)'(x,). Thus we have f'(x,), = (f + g > ' ( ~ o > . ~, , +, , +, , +, , The fact that one does not add velocities this way in the theory of special relativity does not, violate the sum rule. In classical mechanics, velocities are derivatives, but in relativity, velocities, are not simply derivatives, so the formula for their combination is more complicated., , Copyright 1985 Springer-Verlag. All rights reserved.

Page 33 :
"1.4 DiNerentiating Polynomials, , 81, , Exercises for Seelion 1.4, Differentiate the functions in Exercises 1- 12., 1. xI0, 2. x14, 3. ~3~, 4. x S, 5. -5x4, 6. -53x20, 7. 3x1°, 8. 8x'O0, 9. 3 6, 10. 2 / x, 11. - 8 6, 12. - 6 / x, In Exercises 13-16, verify the sum rule for the given, pair of functions., 13. f ( x ) = 3 x 2 6, g ( x ) = x 7, 14. f ( x ) = 8 x 9, g ( x ) = x 2 - 1, 15, f ( x ) = x 2 x 1 , g ( x ) = - 1, 16. f ( x ) = 2 ~ ~ - 3 ~ + 6 , ~ (- xx 2) +, =8x-9, , +, +, + +, , +, , 17. Find a formula for the derivative of f ( x ) 2g(x)., 18. Find a formula for the derivative of 3f ( x ) +, 2g(x)., Differentiate the functions in Exercises 19-22., 19. x 5 8 x, 20. 5 x 3, 21. t 5 + 6t2 8t 2, 22. sI0 8s9 + 5s8 + 2, Differentiate the functions in Exercises 23-34., 23. f ( x ) = x4 - 7 x 2 - 3 x + 1, 24. h ( x ) = 3x" + 8 x 5 - 9 x 3 - x, 25. g ( s ) = sI3 12s' - as7 s4 0s', 26. f ( y ) = -y3 - gY2 - 14y - 4, 27. f ( x ) = x4 - 3x3 2 x 2, 28. f ( t ) = t4 4t3, 29. g ( h ) = 8hI0 h9 - 56.5h2, 30. h ( y ) = ~ y ' O + ~ y ~ - f l y ~, 31. p ( x ) = ( x 2, 32. r ( t ) = ( t 4 2t2)', 33. f ( t ) = ( t 3 - 17t 9)(3t5- t 2 - 1 ), 34. h ( x ) = ( x 4 - 1)(x2 x 2), , +, , + +, , +, , +, , +, , +, +, +, , + +, , +, , +, , + +, 35. Find f'(r) if f(r) = -5r6 + 5r4 - 13r2 + 15., 36. Find g'(s) if g(s) = s7 + 13s6 18s3 + +s2., 37. Find h l ( t )if h ( t ) = ( t 4 + 9)(t3- t)., 38. Differentiate x 5 + 2x4 + 7., 39. Differentiate ( u 4 + 5)(u3+ 7u2 + 19)., 40. Differentiate (3t5 + 9t3 + 5t)(t + 1)., -, , Differentiate the functions in Exercises 41-46., 41. f ( x ) = x 2 - &, , +, , 45. f ( x ) = ( 1 - 6 ) ( 1 6 ), 46. f ( x ) = (1 +&)&, 47. A particle moves on a line with position f ( t ), = 16t2 + (0.03)t4 at time t. Find the velocity at, t = 8., 48. Suppose that the position x of a car at time t is, ( t - 213., (a) What is the velocity at t = - 1,0, l ?, (b) Show that the average velocity over every, interval of time is positive., (c) There is a stop sign at x = 0. A police officer, gives the driver a ticket because there was, no period of time during which the car was, stopped. The driver argues that, since his, velocity was zero at t = 2, he obeyed the, stop sign. Who is right?, 49. Find the slope of the tangent line to the graph of, x4 - x 2 + 3 x at x = 1., 50. Find the slope of the line tangent to the graph of, f ( x ) = x 8 2 x 2 + 1 at (1,4)., For each of the functions in Exercises 51-54, find a, function whose derivative is f ( x ) . (Do not find f'(x).), 51. f ( x ) = x 2, 52. f ( x ) = x 2 + 2 x + 3, 53. f ( x ) = x n ( n any positive integer), 54. f ( x ) = ( x + 3)(x2+ 1), , +, , 55. Verify the constant multiple rule for general quadratic functions, i.e., show that ( k f ) ' ( x )= k f ' ( x ), if f ( x ) = ax2 bx + c., 56. Verify the sum rule for general cubic functions, using the formula for the derivative of a polynomial., 57. Let V ( r ) be the volume V of a sphere as a, function of the radius r. Show that V f ( r )is the, surface area., 58. Let V(1) be the volume of a cube as a function, of I, where 21 is length of one of its edges. Show, that V'(1) is the surface area., *59. Explain the constant multiple rule in terms of a, change of units in distance from miles to kilometers., *60. Show that if two polynomials have the same, derivative, they must differ by a constant., , +, , Copyright 1985 Springer-Verlag. All rights reserved.

Page 34 :
82, , Chapter 1 Derivatives and Limits, , 1.5 Products and Quotients, To dqferentiate a product, difSerenliate each factor in turn and sum the results., We have given general rules for the derivative of a sum and a constant, multiple. We now turn to products and quotients., The product fg and quotient f / g of two functions are defined by, ( f g ) ( x )= f ( x ) g ( x ) and ( f / g ) ( x )= f ( x ) / g ( x ) , the latter being defined only, when g ( x ) # 0.The formulas for (fg)' and ( f / g ) ' are more complicated than, those for ( f + g)' and (kfi', but they are just as straightforward to apply., Before developing the correct formulas, let us convince ourselves that (fg)' is, not f'g'., Example 1, , SolutEon, , Let f ( x ) = x 2 and g ( x ) = x3. Is (fg)' equal to f'g'?, Notice that the product function is obtained simply by multiplying the, ) x5. Thus, (fg)'(x) = 5x4. On the, formulas for f and g: ( f g ) ( x )= ( x 2 ) ( x 3=, other hand, f ' ( x ) = 2x and gr(x)= 3x2, so (f'gl)(x)= f ' ( x ) g f ( x )= 6x3. Since, 5x4 and 6 x 3 are not the same function, (fg)' is not equal to f'g'. A, Example 1 shows that the derivative of the product of two functions is not the, product of their derivatives. We state the correct rule for products now and, discuss below why it is true., , To differentiate a product f(x)g(x), differentiate each factor and multiply it by the other one, then add the two products:, , ( f g I f ( x >= f ( x )g'(x) + f ' ( x ) g ( x >, , Example 2, , (a) Verify the product rule for f and g in Example 1., (b) Verify the product rule for f ( x ) = x m and g ( x ) = x n , where m and n are, natural numbers., , SoluPiss~ (a) We know that (fg>'(x)= 5x4. On the other hand, f(x)gl(x)C f ' ( x ) g ( x ), = (x2)(3x2) (2x)(x3)= 5x4, SO the product rule gives the right answer., (b) By the power rule in Section 1.4, f ' ( x ) = mx " - I and g f ( x )= nx "-I,, so that ( f g ) ' ( x )= f ( x ) g ' ( x ) f ' ( x ) g ( x )= x "( n x" - I ) ( m x " - ' ) x" =, ( n m)xm+"-'. On the other hand, ( f g ) ( x )= x m x n= xm+", so again by, the power rule (fg)'(x)= ( m + n)xm+"-', which checks. A, , +, , +, , +, , +, , The form of the product rule may be a surprise to you. Why should that, strange combination off, g, and their derivatives be the derivative of fg? The, following mathematical justification should convince you that the product rule, is correct., , Copyright 1985 Springer-Verlag. All rights reserved.

Page 35 :
1.5 Products and Quotients, , 83, , Proof of the To find (-fg)'(xn),, - - we take the limit, Product Rule, , lim, , (fg)(xo + Ax) - (fg)(xo), , f(x0 + Ax)g(xo + Ax) - f(xo)g(xo), Ax-0, Ax, Simplifying this expression is not as straightforward as for the sum rule. We, may make use of a geometric device: think of f(x) and g(x) as the lengths of, the sides of a rectangle; then f(x)g(x) is its area. The rectangles for x = xo, and x = xo Ax are shown in Fig. 1.5.1. The area of the large rectangle is, = lim, , +, , Figure 1.5.1 The geometry, behind the proof of the, product rule., , f(xo + Ax)g(xo + Ax); that of the darker rectangle is f(xo)g(xo). The difference f(xo + Ax)g(xo + Ax) - f(xo)g(xo) is the area of the lighter region, which, can be decomposed into three rectangles having areas, , and, Thus we have the identity:, = [ f(xo, , + Ax) - f(xo)] g(x0) + f(xo)[ g(xo + Ax) -, , (If you do not like geometric arguments, you can verify this identity algebraically.), Substituting (2) into (I), we obtain, , By the sum and constant multiple rules for limits, (3) equals, , We recognize the first two limits in (4) as f'(xo) and g'(xo), so the first two, terms give f'(xo)g(xo) + f(xo)gf(xo)-precisely the product rule. To show that, , Copyright 1985 Springer-Verlag. All rights reserved.

Page 36 :
84, , Chapter I Derivatives and Limits, , the third limit, represented geometrically by the small rectangle in the upper, right-hand corner of Fig. 1.5.1, is zero, we use continuity of g (see Section, 1.3). The product rule for limits yields, , Example 3, , +, , Using the product rule, differentiate ( x 2 2x - 1)(x3- 4x2). Check your, answer by multiplying out first., , + +, = (2x4 - 6x3 - 8x2)+ (3x4 - 2x3 - 19x2 + 8 x ), = 5x4 - 8x3 - 27x2 + 8x., +, , = ( 2 ~2 ) ( ~ 3 4 ~ 2 ) ( ~ 2 2~ - 1 ) ( 3 ~28 ~ ), , Multiplying out first,, , +2 2~ - 1 ) ( ~ 3- 4 ~ 2=) x5 - 4 ~ +4 2~~- g x 3, +4 ~ 2, = x5 - 2 ~ 49 ~+, 34~2., The derivative of this is 5x4 - 8x3 - 27x2 + 8x, so our answer cheeks. A, (, , Example 4, , Solution, , ~, , - ~3, , Differentiate x 3 / 2by writing x3/', , =x, , .fiand using the product rule., , We know that ( d / d x ) x = 1 and ( d / d x ) G = 1 / ( 2 6 ) . Thus, the roduct rule, gives, , This result may be written ( d / d x ) x 3 / ' = $ X I / ' , which is another instance of, the rule ( d / d x )( x " ) = nxn- for noninteger n. A, , ', , We now come to quotients. Let h ( x ) = f ( x ) / g ( x ) , where f and g are differentiable at x,, and suppose g(x,) Z 0 so that the quotient is defined at x,. If we, assume the existence of hf(x0),it is easy to compute its value from the product, rule., Since h ( x ) = f ( x ) / g ( x ) , we have f ( x ) = g(x)h(x).Apply the product rule, to obtain, , S'(x0) = gl(xo)h(xo)+ g(xo)hf(xo)., Solving for h'(x,), we get, , Copyright 1985 Springer-Verlag. All rights reserved.

Page 37 :
1.5 Products and Quotients, -, , f'(xo)&!(xo), , -, , 85, , f (xo)g'(xo), , [ g(xo)12, This is the quotient rule., , To differentiate a quotient f(x)/g(x) (where g(x) $; 0), take the derivative of the numerator times the denominator, subtract the numerator, times the derivative of the denominator, and divide the result by the, square of the denominator:, , When you use the quotient rule, it is important to remember which term in the, numerator comes first. (In the product rule, both terms occur with a plus sign,, so the order does not matter.) One memory aid is the following: Write your, guess for the right formula and set g = 1 and g' = 0. Your formula should, reduce to f'. If it comes out as -f' instead, you have the terms in the wrong, order., Example 5, Solution, , Example 6, Solution, , x, Differentiate ----., x3 + 5, By the quotient rule, with f(x) = x 2 and g(x) = x3 + 5,, , Find the derivative of (a) h(x), , = (2x, , + 1)/(x2 - 2) and (b) & / ( I + 3x2)., , (a) By the quotient rule with f(x) = 2x, , + 1 and g(x) = x2 - 2,, , Copyright 1985 Springer-Verlag. All rights reserved.

Page 38 :
88, , Chapter I Derivatives and Limits, , In the argument given for the quotient rule, we assumed that h1(x0)exists;, however, we can prove the quotient rule more carefully by the method of, limits., The derivative of h ( x ) = f ( ~ ) / ~ (atx xo, ) is given by the following limit:, h(x0 + A X )- h(xo), h1(x0)= lim, AX+O, AX, f(x0 + A x ) / g ( x o + Ax) - f(xo)/g(xo), = lim, Ax-0, Ax, , Proof of the, Quotient Rule, , = lim, Ax+O, , f(x0 + Ax)g(xo) - f(xo)g(xo + Ax), g(xo)g(xo + Ax) Ax, , A look at the calculations in the limit derivation of the product rule suggests, that we add -f(xo)g(xo)+ f(xo)g(xo)= O to the numerator. We get, h'(xo)= lim, Ax+O, , =, , -, , lim, , f(x0 + Ax)g(xo) - f(xo)g(xo) + f(xo)g(xo) - f(xo)g(xo + Ax), g(xo)g(xo+ Ax)Ax, g(xo)g(xo + Ax>, , [, , f (xo + Ax) - f (xo), Ax, , g(x0), , I-, , 1, 1 [S'(xo)g(xo)- f(xo>gl(xo), lim g(xo + Ax) g(xo), , (5), , Ax+O, , Since g is differentiable at xo, it is continuous there (see Section 1.3), and so, , lim g ( x o + Ax) = g(xo)., , (6), , Ax-0, , Substituting (6) into (5) gives the quotient rule. B1, Certain special cases of the quotient rule are particularly useful. If f ( x ) = 1,, then h ( x ) = l / g ( x ) and we get the reciprocal rule:, , To differentiate the reciprocal l / g ( x ) of a function (where g ( x ) # 0),, take the negative of the derivative of the function and divide by the, square of the function:, , Example 7, Solutlon, , Differentiate (a) l / ( x 3 + 3x2) and (b) I/(& + 2)., (a), , -, , --, , 1, , d, ( x 3+ 3x2)2 dx, , + 3x2), , -( x 3, , Copyright 1985 Springer-Verlag. All rights reserved.

Page 39 :
1.5 Products and Quotients, , 87, , Combining the reciprocal rule with the power rule from Section 1.4 enables us, to differentiate negative power^.^ If k is a positive integer, then, , = - l ( k x k - l ) = -kx-k-l., , xZk, Writing n for the negative integer - k, we have (d/dx)(xn) = nxn-', just as, for positive n. Recalling that (d/dx)(xO) = (d/dx)(l) = 0, we have established, the following general rule., , If n is any (positive, negative or zero) integer, (d/dx)xn, , Example 8, , =, , nx "-, , I., , (When, , Differentiate 1/x6, , Solution (d/dx)(l/x6), , = (d/dx)(xP6) =, , - 6 ~ - ~ =- '-6x-'., , A, , We conclude this section with a summary of the differentiation rules obtained, so far. Some of these rules are special cases of the others. For instance, the, linear and quadratic function rules are special cases of the polynomial rule,, and the reciprocal rule is the quotient rule for f(x) = 1. Remember that the, basic idea for differentiating a complicated function is to break it into its, component parts and combine the derivatives of the parts according to the, rules., Example 9, Solution, , 2 -5 and (b), Differentiate (a) 3x4 + x, x3, (x2, , 1, , + 3)(x2 + 4), , ', , (a) By the sum, power, and constant multiple rules,, , (b) Let f(x) = (x2 + 3)(x2 + 4). By the product rule, Y(x) = 2x(x2 + 4) +, (x2 + 3)2x = 4x3 + 14x. By the reciprocal rule, the derivative of l/f(x) is, , Students requiring a review of negative exponents should read Section R.3., , Copyright 1985 Springer-Verlag. All rights reserved.

Page 40 :
88, , Chapter 11 Derivatives and Limits, , Example "1 We derived the reciprocal rule from the quotient rule. By writing f ( x ) / g ( x ), = f ( x ) . [ l / g ( x ) ] ,show that the quotient rule also follows from the product, rule and the reciprocal rule., , (This calculation gives another way to reconstruct the quotient rule if you, forget it-assuming, of course, that you remembered the reciprocal rule.) A, , Differentiation Rules, , / The derivative o f, Linear, function, Quadratic, function, Sum, Constant, multiple, Power, , bx, , +, , ax2+ bx, , +c, , I, , f(x) + g(x), , I, , x n { n any integer), , Polynomial c n x n + . - . + c 2 x 2, , + c , x + c,, Product, , In Leibniz notation, , f ( x ) g( x ), , ncnxn-I+-.., +2c2x + c ,, f'(x)g(x)+f(x)gf(x), , +, , +, , +, , -d( c n x n, . . . c,x2 c I x, dx, = ncnxn-I+ - - . +2c2x, c,, d, du, dv, - ( u v ) = -v + u dx, dx, dx, , + c0), , +, , Copyright 1985 Springer-Verlag. All rights reserved.

Page 41 :
1.5 Products and Quotients, , 89, , Exercises for Section "1.5, Compute the derivatives of the functions in Exercises, 1-12 by using the product rule. Verify your answer by, multiplying out and differentiating the resulting polynomials., 1 . ( x 2+ 2)(x + 8), 2. ( x + l ) ( x - 1 ), 3. ( x 4 + x ) ( x 3 - 2 ), 4. ( x 2+ 3x)(2x - 1), 5. ( x 2+ 2x + 1)(x - 1 ), 6. ( x 3 + 3x2 3 x l ) ( x - I), 7. ( x 2 + 2 x + 2 ) ( x 2 + 3 x ), 8. ( x 2+ 4 x + 8)(x2+ 2 x - 1 ), 9. ( x - 1)(x2+ x + 1 ), 10. ( x - 2)(x2 2 x 1 ), 1 1 . ( X - 1 ) ( ~+, 3 x2, I), 12. ( x 3+ 2)(x2+ 2x + 1 ), In Exercises 13-16, differentiate the given function by, writing it as indicated and using the product rule., 13. x ~ =/x 2~.&, 14. x = & . G, 15. x7/* = x 3 .&, 16. x 2 =, .x ~ / ~, Differentiate the functions in Exercises 17-30., , Differentiate the functions in Exercises 39-46., , + +, , + +, + +, , 5, , 47. Use the reciprocal rule twice to differentiate, I / [ l / g ( x ) ]and show that the result is gl(x)., 48. Differentiate x m / x n by the quotient rule and, compare your answer with the derivative of, xm-" obtained by the power rule., 49. Find the slope of the line tangent to the graph of, f ( x ) = I / & at x = 2., 50. Find the slope of the line tangent to the graph of, f ( x ) = ( 2 x 1)/(3x + 1) a t x = 1., Let f ( x ) = 4 x 5 - 13x and g ( x ) = x 3 + 2 x - 1. Find the, derivatives of the functions in Exercises 51-56., 51. f ( x ) g ( x ), 52. [f ( x ) + x 3 - 7 x I [ g ( x ) l, 53. x f ( x ) + g ( x ), , +, , Find the indicated derivatives in Exercises 31-38., *57. Let P ( x ) be a quadratic polynomial. Show that, ( d / d x ) ( l / P ( x ) )is zero for at most one value of, x in its domain. Find an example of P ( x ) for, which ( d / d x ) ( l / P ( x ) ) is never zero on its domain., *58. Calculate the following limits by expressing each, one as the derivative of some function:, x8 - x7 + 3x2 - 3, (a) lim, x-t l, x-1, 1 / x 3 - 1/23, (b) lim, x+2, x -2, ', x2+x, (c) lim, ,+-I, ( x +2)(x 1 ) ', , +, , Copyright 1985 Springer-Verlag. All rights reserved.

Page 42 :
98, , Chapter 1 Derivatives and Limits, , 1.6 The Linear Approximation, and Tangent Lines, A good approximation to f(xo + Ax) is f ( x o ) + f'(xo)Ax., , Section 1.1, we saw that the derivative f'(x,) is the slope of the tangent line, the graph y = f(x). This section explores the relationship between the graph, f and its tangent line a little further., Recall from Section R.4 that the equation of the straight line through, ( x , , yo) with slope m is, y = y o + m ( x - x,)., In particular we get the following formula for the tangent line t o y = f ( x ) (see, Figure 1.6.1)., , line to the graphy = f(x) at, , I, , I, , P, , (xo,f(x0))., , x0, , X, , The equation of the line tangent toy, , Y, , = f(x0) + f'(xo)(x, , =f(x), , at ( x , , f(xo)) is, , - xo)., , 6+, , (a) Find the equation of the line tangent to the graph y =, 1 / ( 2 ( x + 1)) at, x = I., (b) Find the equation of the line tangent to the graph of the function, f ( x ) = ( 2 x + 1 ) / ( 3 x 1 ) at x = 1., , Example 1, , +, , Solution, , (a) Here xo = 1 and f ( x ), , =, , 6 + 1 / 2 ( x + 1). We compute, , +, +, , Since f ( l ) = 1 + = $, the tangent line has equation y = 2 $ ( x - I), i.e.,, + 7., (b) By the quotient rule, f ' ( x ) equals [2(3x 1) - ( 2 x 1 ) 3 ] / ( 3 x 1)2, = - 1 / ( 3 x + I ) ~ .The equation of the tangent line is, , 4, , 8y = 3 x, , y, , =f ( 1 ), , +, , +f ' ( l ) ( x - 1 ) = 2 - $ ( x, , ory= - $ x + # ., , -, , 1), , .+&, , Copyright 1985 Springer-Verlag. All rights reserved., , +

Page 43 :
1.8 The Linear Approximation and Tangent Lines, , Example 2, Solution, , 91, , Where does the line tangent t o y = 6 at x = 2 cross the x axis?, Here dy/dx = 1 / 2 6 , which equals 1 / 2 n at x = 2. Since y = 6 at x = 2,, the equation of the tangent line is, , =a, , This line crosses the x axis when y = 0 or 0, + (1/2n)(x - 2)., Solving for x, we get x = -2. Thus the tangent line crosses the x axis at, x = -2. A, We have used the idea of limit to pass from difference quotients to derivatives., We can also go in the other direction: given f(x,) and f'(x,), we can use the, derivative to get an approximate value for f(x) when x is near x,., According to the definition of the derivative, the difference quotient, Ay/Ax = [f(x, + Ax) - f(xo)]/Ax is close to f'(xo) when Ax is small. That is,, the difference, , is small when Ax is small. Multiplying the preceding equation by Ax and, rearranging gives, , Suppose now that we know f(xo) and f'(x,) and that we wish to evaluate f at, the nearby point x = x, + Ax. Formula (1) expresses f(x) as a sum of three, terms, the third of which becomes small-even compared to Ax-as Ax -+ 0., By dropping this term, we obtain the approximation, , In terms of x = x,, , + Ax, we have, , The right-hand side of (3) is a linear function of x, called the linear approximation to f at x,. Notice that its graph is just the tangent line to the graph off at, (x,, f(x,)). (See Fig. 1.6.2.), , Linear approximation, , F i w e 1.6.2. AS AX, approaches zero, the, difference between f(x) and, the approximation, f(xo) + f'(xo)(x - xo), becomes arbitrarily small, compared to Ax = x - x,., , Difference between, I, , linear approximation, , Copyright 1985 Springer-Verlag. All rights reserved.

Page 44 :
92, , Chapter 1 Derivatives and Limits, , The linear approximation is also called the first-order approximation., Second-order and higher-order approximations are introduced in Section 12.5., Example 3, , Solullon, , (a) Show that the linear approximation to (x, +, is x i + 2xoAx. (b), Calculate an approximate value for (1.03)~.Compare with the actual value., Do the same for (1.0003)~and (1.00000~3)~., (a) Let f(x) = x2, so f'(x) = 2x. Thus the linear approximation to f(xo + Ax), is f (xo) + f'(xo) Ax = x i + 2xoAx., (b) Let x, = 1 and Ax = 0.03; from (a), the approximate value is 1 + 2 Ax =, 1.06. The exact value is 1.0609. If Ax = 0.0003, the approximate value is, 1.MI06 (very easy to compute), while the exact value is 1.00060009 (slightly, harder to compute). If Ax = 0.0000003, the approximate value is 1.0000006,, while the exact value is 1.00000060000009. Notice that the error decreases, even faster than Ax. A, , For x near x,, f(xo) + f'(xo)(x - xo) is a good approximation for f(x)., f (xo + Ax) =f (x,) + f'(xo) Ax or Ay wfl(xo) Ax, , 8 Example 4 Calculate an approximate value for the following quantities using the linear, approximation around x,, , Solullon, , = 9., , Compare with the values on your calculator., , Let f(x) = 6 and recall that f'(x), , =, , 1 / 2 6 . Thus the linear approximation is, , f(x0 + Ax)=f(xo) +f'(xo>Ax,, I.e.,, , J ~ F z & + ~ A x ., 2J;rd, (a) Let x,, , =9, , and Ax, , = 0.02, so, , xo + Ax, , = 9.02., , Thus, , On our calculator we get 3.00333 15., (b) Let xo = 9 and Ax = 1 ; then, , On our calculator we get 3.1622777., (c) Let xo = 9 and Ax = - 0.18; then, , On our calculator we get 2.9698485., , Copyright 1985 Springer-Verlag. All rights reserved.

Page 45 :
4.6 The Linear Approximation and Tangent Lines, , 93, , (d) Let x, = 9 and Ax = - 1 ; then, , On our calculator, we get 2.828427 1., Notice that the linear approximation gives the best answers in (a) and (c),, where Ax is smallest. A, Example 5, , Calculate the linear approximation to the area of a square whose side is 2.01., Draw a geometric figure, obtained from a square of side 2, whose area is, exactly that given by the linear approximation., , Solution, , A = f(r) = r2. The linear approximation near r, = 2 is given by f(r,), f'(r,), (r - r,) = r,2 2ro(r - r,) = 4 + 4(r - r,). When r - r, = 0.01, this is 4.04., , +, , +, , t---, , 2.01-4, Total area:, square + two strips =, 4 + 2(0.02) = 4.04, , Figure 1.63. The linear, approximation to the, change in area with respect, to a side has error equal to, the shaded area. (Diagram, not to scale.), , Area of each strip:, 2(0.01) = 0.02, , The required figure is shown in Fig. 1.6.3. It differs from the square of side, 2.01 only by the small shaded square in the corner, whose area is (0.01)~=, 0.0001. A, , D Example 6, , Calculate an approximate value for, 2, and compare with the numerical value on your calculator., , Solution, , We let f(x) = 2 / ( 6 + x2) and note that we are asked to calculate f(l - 0.01)., By the linear approximation,, f ( l - 0.01) w f(1) - f'(1)(0.01)., Note that f ( l ), , =, , 1. We calculate f'(x) by the quotient rule:, , On our calculator we find f(0.99) = 1.0 126134, in rather good agreement. A, , Copyright 1985 Springer-Verlag. All rights reserved.

Page 46 :
94, , Chapter I Derivatives and Limits, , Exercises lor Section 1.6, In Exercises 1-4, find the equation of the line tangent, to the graph of the given function at the indicated point, and sketch:, 1. y = 1 - x 2 ; x 0 = 1, 2. y = x 2 - x ; x,= 0, 3. y = x 2 --2 x + 1 ; xo = 2, 4. y = 3x2 + I - x ; X o = 5, Find the equation of the tangent line to the graph of, f ( x ) at (x,, f ( x o ) ) in Exercises 5-8., , 5. f ( x ) = ( x 2 - 7 ) - 3 X ; x o = O, x+2, , In Exercises 9-12, find where the tangent line to the, graph of the given function at the given point crosses, the x axis., 9.y=;x0=I, x+l, , 11. y = -, , ;X0=4, , Calculate approximate values in Exercises 29-32., 29. ( x 2 + 3 ) ( x + 2) if x = 3.023, , 33. Find the equation of the line tangent to the, graph of f ( x ) = x 8 + 2 x 2 + 1 at (1,4)., 34. Find the equation of the tangent line to the, graph of x 4 - x 2 + 3 x at x = 1 ., 35. Find the linear approximation for 1/0.98., 36. Find the linear approximation for 1/ 1.98., Calculate approximate values for each of the quantities, in Exercises 37-40., 37. s4 - 5s3 + 3s - 4 ; s = 0.9997, , a., , 1 +,G, 12. y=x(\l;; + 1 ) ; x o = 1, 8 Calculate an approximate value for each of the, squares in Exercises 13-16 and compare with the exact, value:, 13. (2.02)~, 14. (199)2, 15. (4.999)2, 16. ( - 1.002)', B In Exercises 17-20, calculate an approximate value, for the square root using the linear approximation at, xo = 16. Compare with the value on your calculator., 17. {, =, 18., 19. ,KE, 20. ,InUsing the linear approximation, find an approximate, value for the quantities in Exercises 21-24., 22. (1.031~, 21. (2.94)4, 23. (3.991~, 24. (101)8, 25. The radius of a circle is increased from 3 to 3.04., Using the linear approximation, what do you, find to be the increase in the area of the circle?, 26. The radius r of the base of a right circular, cylinder of fixed height h is changed from 4 to, 3.96. Using the linear approximation, approximate the change in volume V., 27. A sphere is increased in radius from 5 to 5.01., Using the linear approximation, estimate the increase in surface area (the surface area of a, sphere of radius r is 4sr2)., 28. Redo Exercise 27 replacing surface area by volume (the volume inside a sphere of radius r is, $ sr3)., , 41. Let h ( t ) = -4t2 + 7 t + Use the linear approximation to approximate values for h(3.001),, h(1.97), and h (4.03)., 42. Let f ( x ) = 3 x 2 - 4 x + 7. Using the linear approximation, find approximate values for f(2.02),, f(1.98), and f(2.004). Compute the actual values, without using a calculator and compare with the, approximations. Compare the amount of time, you spend in computing the approximations with, the time spent in obtaining the actual values., 43. Let g ( x ) = - 4 x 2 + 8 x + 13. Find g1(3). Show, that the linear approximation to g(3 + A x ) always gives an answer which is too large, regardless of whether Ax is positive or negative. Interpret your answer geometrically by drawing a, graph of g and its tangent line when x , = 3., 44. Let f ( x ) = 3 x 2 - 4 x + 7. Show that the linear, approximation to f(2 + Ax) always gives an answer which is too small, regardless of whether Ax, is positive or negative. Interpret your answer, geometrically by drawing a graph of f and its, tangent line at x , = 2., a45. Let f ( x ) = x4., (a) Find the linear approximation to f(x) near, x = 2., (b) Is the linear approximation larger or smaller, than the actual value of the function?, (c) Find the largest interval containing x = 2, such that the linear approximattion is accurate within 10% when x is in the interval., a46. (a) Give numerical examples to show that linear, approximations to f ( x ) = x 3 may be either, too large or too small., , Copyright 1985 Springer-Verlag. All rights reserved.

Page 47 :
Review Exercises for Chapter 1, (b) Illustrate your examples by sketching a, graph of y = x 3 , using calculated values of, the function., 47. Show that a good approximation to 1/(1 x ), when x is small is I - x., +48. If you travel 1 mile in 60 x seconds, show that, a good approximation to your average speed, for, x small, is 60 - x miles per hour. (This works, quite well on roads which have mileposts.) Find, , +, , +, , 95, , the error in this approximation if x = 1, - 1,5,, - 5, 10, - 10., , &! 49. Return to Exercise 47. Show experimentally that, , a better approximation to 1/(1 + x ) is 1 - x +, x2. Use this result to refine the speedometer, checking rule in Exercise 48., n50. Devise a speedometer checking rule for metric, units which works for speeds in the vicinity of, about 90 or 100 kilometers per hour., , Review Exercises for Chapter 1, Differentiate the functions in Exercises 1-20., 1. f ( x ) = x 2 - 1, 2. f ( x ) = 3x2 2 x - 10, 3. f ( x ) = x 3 + 1, 4. f ( x ) = x 4 - 8, 5. f ( x ) = 2 x - 1, 6. f ( x ) = 8 x 1, 7. f ( s ) = s2 + 2s, 8. f ( r ) = r4+ 10r 2, 9. f ( x ) = - l o x 5 + 8 x 3, 10. f ( x ) = 12x3 + 2 x 2 + 2 x - 8, 1 1 . f ( x ) = ( x 2- 1)(x2+ 1), 12. f ( x ) = ( x 3+ 2x 3)(x2+ 2), 13. f ( x ) = 3 x 3 - 2 6, 14. f ( x ) = x 4 9 6, , +, , +, , +, , +, , +, , 35. lim, h-0, , ( h - 2)6 - 64, h, , 36. lim, h+O, , ( h - 216, h, , + 64, , 37. lirn 3x2 + 2x, 38. lirn 3x2 + 2 x, x-3, x, x+o, x, ( s + 319 - 39, x2-9, 39. lim 40. lim, x-t3 X - 3, s-to, S, f ( x + Ax> - f ( x >, 41. lirn, Ax+O, AX, where f ( x ) = x4 + 3 x 2 + 2, f ( x + Ax> - f ( x >, AX, where f ( x ) = 3 x s - 8x7 + 10., , 42. lirn, , Ax40, , 43. lirn, , 3&+2, -, , 5&+ 1, 5x2+ 4, 45. lim 5x3 + 9, "jrn, , "jrn, , +, +, +, +, , 5x2 4, 44. lirn X+rn, 3x2 9, 5x', 4, 46. lim X+rn, 5x2 9, , 47. For the function in Fig. l.R.l, find lim,,xo f ( x ), for x , = - 3, - 2, - l,O, 1,2,3. If the limit is not, defined or does not exist, say so., , Find the derivatives indicated in Exercises 2 1-30., , Figure 1.R.1. Find, limx+xof ( x ) at the, indicated points., Find the limits in Exercises 31-46., x 3-+-1, 32. lirn x+l, , x-l, , x3- 1, 33. lirn x+l, , X - 1, , X, , +1, , x5- 1, 34. lirn -x+l X - 1, , Copyright 1985 Springer-Verlag. All rights reserved.

Page 48 :
96, , Chapter 4 Derivatives and Limits, , 48. Do as in Exercise 47 for the function in Fig., 1 .R.2., , Calculate approximate values for the quantities in Exercises 63-70 using the linear approximation., 63. (l.009)s, 64. ( - 1 .008)4 - 3( - 1.008)3+ 2, 65. d, m, 66., 3x3 - l o x 2 8x 2, 67. f(2.003) where f ( x ) =, , +, , +, , X, , 68. g(1.0005) where g ( x ) = x 4 - 10x3., 69. h(2.95), where h ( s ) = 4s' - s4., , Find the equation of the line tangent to the graph of the, function at the indicated point in Exercises 71-74., 71. f ( x ) = x 3 - 6 x ; (0,O), , Figwre 1.R.2. Find the limit, at the indicated points., , 49. Use the limit method directly to find f ' ( l ) , where, f ( x ) = 3x3 + 8 x ., 50. Use the limit method directly to compute, ( d / d x ) ( x 3 - 8 x 2 )at x = - 1., 5 1 . Use the limit method directly to compute, ( d / d x ) ( x - 6)., 52. Use the limit method directly to compute the, derivative of f ( x ) = x3 - f ., Find the slope of the tangent line to the graphs of the, functions in Exercises 53-58 at the indicated points., 53. y = x 3 - 8 x 2 ; xo = 1, 54. y = x4 + 2 x ; x , = - 1, 55. = ( x +~ I ) ( x ~ 1); xo = o, 56. y = x4 + l o x + 2; x, = 2, 57. = 3 ~ -4 l o x 9 ; xo = o, 58. y = 3 x + 1 ; x o = 5, 59. Two long trains, A and B, are moving on adjacent tracks with positions given by the functions, A ( t ) = t 3 + 2t and B ( t ) = 7 t 2 / 2 + 8. What are, the best times for a hobo on train B to make a, moving transfer to train A?, 60. A backpack is thrown down from a cliff a t t = 0., It has fallen 2t + 4.9t2 meters after t seconds., Find its velocity at t = 3., 61. A bus moving along a straight road has moved, f(t) = ( t 2+ f i ) / ( l + fi) meters after time t (in, seconds). What is its velocity at t = I?, 62. A car has position x = ( f i - 1 ) / ( 2 f i 1) at, time t. What is its velocity at t = 4?, , +, , 75. A sphere is increased in radius from 2 meters to, 2.01 meters. Find the increase in volume using, the linear approximation. Compare with the exact value., 76. A rope is stretched around the earth's equator. If, it is to be raised 10 feet off the ground, approximately how much longer must it be? (The earth, is 7,927 miles in diameter.), In Exercises 77-80, let f ( x ) = 2 x 2 - 5 x + 2, g(x) =, + x 2 2 x and h ( x ) = - 3 x 2 + x 3., 77. Find the derivative of f ( x ) g ( x ) at x = 1., 78. Find the derivative of 3 f ( x )- 2 h ( x ) at x = 0., 79. Find the equation of the tangent line to the, graph of f(x) at x = 1., 80. Find the equation of the tangent line to the, graph of g ( x ) at x = - 1., , +, , +, +, , 81. Let B be a rectangular box with a square end of, side length r. Suppose B is three times as long as, it is wide. Let V be the volume of B. Compute, dV/dr. What fraction of the surface area of B is, your answer?, 82. Calculate lim ,_(,x,- J-), and interpret, your answer geometrically by drawing a right, triangle with hypotenuse of length x and short, leg of length a., 83. Suppose that z = 2y2 + 3y and y = 5 x i1., (a) Find d z / d y and d y / d x ., (b) Express z in terms of x and find d z / d x ., (c) Compare d z / d x with ( d z / d y ) . ( d y / d x ) ., (Write everything in terms of x . ), (d) Solve for x in terms of y and find d x / d y ., (e) Compare d x / d y with d y / d x ., , Copyright 1985 Springer-Verlag. All rights reserved.

Page 49 :
Review Exercises for Chapter 1, , 84. Differentiate both sides of the equation, , and show that you get the same result on each, side., *85. Find the equation of a line through the origin,, with positive slope, which is tangent to the parabola y = x 2 - 2x + 2., *86. Prove that the parabola y = x 2 has the optical, focusing property mentioned in Section R.5. (This, problem requires trigonometry; consult Section, 5.1 for a review.) Hint: Refer to Fig. 1.R.3 and, carry out the following program:, (a) Express tan @ and tan 0 in terms of x., (b) Prove that 90" - 8 = 8 - @ by using the trigonometric identities:, , 97, , dicular to the paper and rotate it until the graph, and its reflection together form a differentiable, curve through P. Draw a line I along the edge of, the mirror. Then the line through P perpendicular, to I is the tangent line. (See Fig. 1.R.4.) Justify, this procedure., Wrong, , tan 28 = 2 tan 0, 1 - tan28, and, 1, -, , tan @, , Figure 1.R.4. Wow to draw a tangent line with a mirror., , ', , +, , Figure 1.R.3. The geometry needed to prove that the, parabola has the optical focusing property., , *89. The polynomial a n x n an- , x "- + . . . + a, is, said to have degree n if an =+0. For example:, deg(x3 - 2x 3) = 3, deg(x4 5) = 4, deg(0x2 +, 3x 1) = 1 . The degree of the rational function, f(x)/g(x), where f(x) and g(x) are polynomials,, is defined to be the degree off minus the degree, of g., (a) Prove that, if f(x) and g(x) are polynomials,, then deg f(x)g(x) = deg f(x) + deg g(x)., (b) Prove the result in part (a) when f(x) and, g(x) are rational functions., (c) Prove that, if f(x) is a rational function with, nonzero degree, then deg f'(x) = deg f(x) 1. What if deg f(x) = O?, *90. Show that f(x) = x and g(x) = 1/(1 - x) obey, , *87. Prove that the parabola y = ax2 has the optical, focusing property. (You should start by figuring, out where the focal point will be.), *88. The following is a useful technique for drawing, the tangent line at a point P on a curve on paper, (not given by a formula). Hold a mirror perpen-, , the "false product rule" (fg)'(x) = f'(x)gf(x)., *91. (a) Prove that if f / g is a rational function (i.e., a, quotient of polynomials) with derivative zero,, then f / g is a constant., (b) Conclude that if the rational functions F and, G are both antiderivatives for a function h,, then F and G differ by a constant., , +, , +, , +, , ?, , Copyright 1985 Springer-Verlag. All rights reserved.