Page 1 :
Arman Sir ), MSc. (Physics) B.Ed., , 85111 24210, 97242 74210, si, ww, - ™ Class 8th To 12th (Science), +, , © ™ Boards (ICSE, CBSE, GSEB), , ALPHAPLUS 1 IT-4€€ (Mains + Advance), , EDUCATIONCENTRE |, IGRITING YOUNG MINDS. " NEET - AIMS |, , |, , J, , , , * cuscer, Kalawad Road, Rajkot., , , , Electrostatics, , , , , , , , Fundamentals, Concepts and Synopsis |, , , , 1., , 2., , Charge, , (a) Quantization, Charge is always in the form of an integral multiple of electronic charge and never its fraction., q = +ne where n is an integer and e = 1.6 x 107'? coulomb = 1.6 x 10°C, Charge on electron/proton is the minimum charge., , 2e le 2e, (b) Particles, known as quarks, are predicted theoretically by Gell-Mann and Zweig. Quarks contain charges > ea 3, , Nobel prize declared in 2004 refers to quarks., (c) Millikan’s oil drop experiment showed the discrete nature of charge. Charge cannot be fractional multiple of e., (d) Charge on an electron is —ve. e = — 1.6 x 107°C, Charge on a proton_is + ve-e =+1.6 x 107°C., Total charge = + ne., (e) A particle/body is positively charged because it loses electrons or it has shortage of electrons., (f) A particle is negatively charged because it gains electrons or it has excess of electrons., (g) Conservation of charge —The total net charge of an isolated physical system always remains constant. Charge can, neither be created nor destroyed. It can be transferred from one body to another., , Coulomb’s inverse square law, , - | Ah, (@ F Ane, r?, , is a constant known as permittivity of free space. Free space is vacuum and may be deemed to be air practically., 2 2, — met N-m, () 1 =9 « 10° newton — metre =9 x 10?, , Ane, coulomb? e, (c) If free space is replaced by a medium, then €, is replaced by (EK) or (,€,) where K is known as dielectric constant, , or relative permittivity or specific inductive capacity (S.I.C) or dielectric coefficient of the medium/material/matter., Thus, , 14% _ 1 4% _ | Nh, , where F denotes the force between two charges, g, and g, separated by a distance r in free space. E, , d) K= = ore,= =, (d) Ep or €, e, K = 1 for vacuum (or air). K = © for conductor/metal., , (€) & = 8.85 x 107? C2 N) M7 and dimensional formula (MILSTtA?], (£) Vector form of the law (q, and q, are like charges)., , , , , , , , , , Bo | as 1 442 = = __l Whee RY, , Gi) Fi = some i FQy Ka = > 7 Ci 2 :, 2 4ney Anty | -F | R, 2,, ss a, 1p |., , Gi) Ay 2 82 =e hn +4, +9), , Ane, | - FI Ane i
Page 2 :
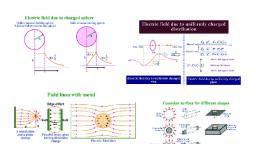
(g) If rj is a unit vector pointing from q, to 9, then, , , , as oe 1 @ F,= a ig ra = force on g, by q,. When gq, > 0 for like charges., MEQ rp,, oe 1 qq, ii) Fy = aie 2 ri2 = force on g, by q, for like charges when 19> 9, 0 72, , intensity/strength of electric field, , (a) Intensity at a point is numerically equal to the force acting on a unit positive charge placed at the point, , , , , , z_F, aur, E ai if q) =1 (unit charge), E =F, 0, , and at any point is directed in the direction of force experienced by a unit +ve charge placed at that point., (b) It is a vector quantity., , (c) The units of intensity E are NC-', volt/metre., (d) The dimensions of E are [ML? T? A-!], (e) Intensity due to a charge g at distance r, I, Ane r, 1 q. Hate, & a, ane,K 72 if point is in the medium., , If q is positive, then # is directed away from it and if q is negative, then ~ is directed towards it., (f) Potential (V) and Intensity (E), , , , (i) B= 7 - It acts in the direction in which a + ve charge moves., , i) B=, , , , aVv, ji) B= OF when potential varies with respect to distance, , where negative sign shows that £ points always in the direction of decreasing potential., Potential difference V, , , , , , (ii) E= ——{—— = = when potential difference is constant., distance Fe, , (iii) Potential at a point distant r from charge q., , v= 1g@ in free space, , Ane, r, , i q. ., , VE = in medium., w) AneyK r, (v) Potential is a scalar quantity., , E-dr =dV., , (g) From positively charged surface, £ acts outwards at right angles i.¢., along outward drawn normal., (h) Intensity is equal to flux (number of electric lines of force) crossing unit normal area., , Flux (9), , Area (8), , Electric lines of force |, , (a) Electric lines of force start from positive charge and terminate on negative charge., , (b) From a positively charged conducting surface, lines of force are normal to surface, in outward direction., , (c) Electric lines of force about a negative point charge are radial, inwards and, outwards., , (d) Electric lines of force are always perpendicular to an equipotential surface., , (e) These lines of force contract along the length but expand at right angles to their length. There is longitudinal tension, , and lateral pressure in a line of force. Contraction shows attraction between opposite charges while expansion indicates, that similar charges repel., , E=, , about a positive point charge are radial,, , (f) The number of electric lines of force (flux) passing through unit normal area at any point indicates electric intensity at, that. point.
Page 3 :
i ic lines of force are., (g) These may be open or closed curves. They are not necessarily closed as magnetic | ), , (h) Two lines of force never intersect or cut each other. ;, (i) Lines of force are parallel and equally spaced in a uniform field., @ Tangent to the curve at a point shows direction of field., , Gauss law ; fart:, (a) For a closed surface enclosing a net charge g, the net electric flux emerging out is given Dy, fee 1., o=QE-ds=*, ees, , (b) If a dipole is enclosed by a closed surface, flux @ is equal to zero., , Here the algebraic sum of charges (+ q — q = 0) is zero. :, (c) The flux will come out if + ve charge is enclosed. The flux will enter if negative charge is enclosed., (d) Flux from a cube, , (i) If q is at the centre of cube, total flux (6) =, , , , £9, (ii) From each face of cube, flux = of ma eS, Eo +O, (e) Electric field due to charged shell VS, . = Q, i) At an external point, E = ., ® Sethe 4negr?, , This is the same as the field when point charge is at centre., Gi) At a point on surface of shell. This is Eis, , , , tne, -Again the shell behaves like a point charge placed at’centre., TLE,, , (iii) At an inside point. (r’ < R), E = 0., Thus a charge q placed inside a charged shell does not experience any force due to the shell., (f) Gaussian surface, (i) for a sphere or spherical shell—A concentric sphere., (ii) for cylinder or an infinite rod—A coaxial cylinder., (iii) for a plate—A cube or a cuboid., , Potential and intensity due to a charged conducting sphere (or shell)., (a) At a point outside the charged sphere, , q ., Defi, dea (r > radius of sphere R)., , 14, , TEg Fr, (b) At a point on the surface of charged sphere, , (i) Intensity £ =, , , , (ii) Potential V = a, , 7 : Ig *, (i) Intensity E = ne, RE (r = Radius of Sphere R), , a evrre ged @., (ii) Potential V ane, R, (c) At a point inside the sphere (r < radius of sphere), , (i) Intensity £ = zero, , , , nt : Ig, te = 4, (ii) Potential V Fe, , , , is is sa :, (@) At the centre of sphere me as potential at the Surface of sphere., (i) Intensity E = zero
Page 4 :
e Speers AE og, (ii) Potential V ane, R, (e) At infinity, (i) Intensity E = zero, (ii) Potential V = zero, , Electric field and potential due to charged non-conducting sphere., (a) Outside the sphere when distance r > radius R, , * ea. : 1, (i) Electric intensity E = +t, , , , Amey r?, zi - i lq, (ii) Electric potential y= ——+4 ;, Tg r E, (b) On the surface of the sphere when distance r = R., log Maxiamum [2 Maximum /:, Gi) Electric intensity £ = ans, RE, , . . 1, (ii) Electric potential V = anes 2, (c) Inside the sphere when distance r < R, , , , q, , i) Electric intensity E = ———>r, (i) Elect intensity ane, RD, , , , ‘ = liq, Vectorially, E = ane) RP, , , , 7, , 7 ‘ ia y= OR - 7), (ii) Electric potential V = ane oR, (d) At the centre of sphere when r = 0, , (i) Electric intensity E = zero, , lq, , , , 3, a A ial P= =, (ii) Electric potential 2 ane, R, , 3 ;, Potential at centre = z* Potential at surface., (e) At infinity, (i) Intensity = zero, (ii) Potential = zero., , Electric dipole, (a) Two equal and opposite charges (q) each, separated by a small distance (D constitute an elect, atoms/molecules are dipoles. 7, (b) (i) Dipole moment P= 9x (Z), (ii) Dipole moment is a vector quantity and is directed from —ve to s+ve charge., (iii) The direction of > is from negative charge to positive charge., (iv) Unit of dipole moment = coulomb metre = C m, , ric dipole. Many of the, , , , ; B P, (v) Dimension of dipole moment = [ATL] Ae—p—* + __»P, (©) Intensity of electric field due to a dipole ; so, @_ Along axis at distance r from centre of dipole Sere, 2 1, B= oP., , 3, r Ane,
Page 5 :
Direction of E is along the direction of dipole moment., (ii) Along equator of dipole at distance r from centre, , pil, , r 4ne,, Direction of £ is antiparallel to direction of p., , (ii) At any point along direction 0., , E= Zvi +3cos” 0, r TE, , The direction E makes an angle B with the line joining the point with centre of dipole, , , , , , 1, where tan B = 3 tan 6., , (d) Torque on a dipole = pE sin 6 numerically. Vectorially, Torque (t) = Px #, The torque tends to align the dipole in the direction of field., Torque is maximum when @ = 90°. Dipole is perpendicular to E., Maximum torque = pE., (e) In uniform electric field, when 6 = 0° or 180° then Tin = 0., (i) The resultant electric force on dipole = zero., Net force= gE — gE = 0, (ii) Two forces [gE and (— qE)] equal opposite and parallel, separated by a distance constitute Ey é, a couple (torque)., , , , This direction of t is perpendicular to the plane containing ? and E., , (iii) When dipole is parallel to electric field, it is in stable equilibrium. When it is antiparallel, to electric field, it is in unstable equilibrium., , (iv) Work done in rotating the dipole from-an angle 6, to angle @, from equilibrium position, W = pE (cos ®, — cos 0,) = — pE (cos 8, — cos 0,), (A) If 6, = 0° and ©, = 180°, W= 2pE, (B) If 6, = 0° and 6, = 90°, W= pE, , (v) Potential energy of dipole, when it is turned through an angle @ from field direction is, , U=-—pE cos 8 =— p-E, (A) If 8 = 0°, U=— pE. This is minimum value of U. The dipole orients itself parallel to field., (B) If 6 = 90°, U=0.This is maximum value of U., (C) If @ = 180°, U= pL., , (vi) Variation of potential energy of dipole with angle 0, between & and P, is shown in PE, , the figure., (A) PE. is negative from 0 to 1/2 and 3n/2 to 2n. They are regions of stable, , equilibrium of dipole., (B) P.E. is positive from 1/2 to 3/2. This is the region of unstable equilibrium of the, , , , dipole., (vii)Dipole in non-uniform electric field, , (A) In non-uniform electric field, the two ends of dipole are acted upon by forces as gE, and, ~q£z, They are not equal as £, # £, in non-uniform field, Hence a force and a torque both act on the dipole., , (B) Force acting on the dipole can be represented by j? = px ae, Broadly speaking, a, ‘Net force = (gE, - gE) along direction of greater field intensity., , (C) On account of net force upon dipole, it may undergo ‘linear motion., , (D) In a non-uniform electric field, a dipole may, therefore, undergo rotation as well as linear:motion