Page 1 :
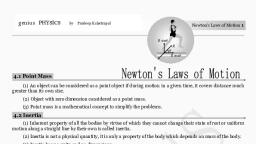
CBSE New Pattern ~ Physics 11th (Term-I), , 77, , 05, Laws of Motion, Quick Revision, 1. Momentum Momentum of a body is the, quantity of motion possessed by the body. It, is defined as the product of its mass m and, velocity v and is denoted by p., Momentum, p = m v, 2. Conservation of Momentum According, to this principle, “In the absence of an, external force, the total momentum of a, system remains constant or conserved and, does not change with time”., If S Fext = 0, then momentum p = constant., 3. Equilibrium of a Particle The forces, acting at the same point or on a particle are, called concurrent forces., These forces are said to be in equilibrium,, n, , when their resultant is zero, i.e., , åF, , i, , = 0., , i = 1, , 4. Lami’s Theorem According to this, theorem, when three concurrent forces F1,, F2 and F3 acting on a body are in, equilibrium, then, F1, F, F, = 2 = 3, sin a sin b sin g, F1, , F2, , γ, β, , α, F3, , 5. Tension When a body of mass m is fastened with, the string, then the weight of the body acts, downwards while a force acting just opposite to, the downward force for balancing it is called, tension., T, mg, , T = mg, where, g = acceleration due to gravity, and, T = tension in the string., 6. Friction Whenever a body moves or tends to, move over the surface of another body, a force, comes into play which acts parallel to the surface, of contact and opposes the relative motion., This opposing force is called friction., 7. Types of Friction, ● Static Friction Force of friction which comes, into play between two bodies, before one body, actually starts moving over the other is called, static friction and it is denoted by f s ., ●, , Limiting Friction Maximum value of static, friction which comes into play when a body just, starts moving over the surface of another body is, called limiting friction., Thus, f s £ f s (max), The value of limiting static friction f s (max), between two given surfaces is directly

Page 2 :
N, θ, Applied, force, F, , fs, , Mg, , 9. Angle of Repose The minimum angle of, inclination of a plane with the horizontal, such, , ax, , that the body placed on the plane just starts to, slide down is known as angle of repose., (f, s), , m, , R, , θ, Mg cosθ, , θ, s in, M, g, , proportional to the normal reaction (R ), between the two surfaces., i.e., f s (max) µ R, f s (max), Þ, f s (max) = m s R Þ m s =, R, The proportionality constant m s is called, coefficient of static friction., ● Kinetic Friction Kinetic friction or, dynamic friction is the opposing force that, comes into play when one body is actually, moving over the surface of another body., Thus, kinetic friction opposes the relative, motion. The value of kinetic friction f k is, given as, f, or, f k = mk R Þ mk = k, R, The proportionality constant mk is called, coefficient of kinetic friction., When the relative motion has begun, the, acceleration of the body on the rough, surface is given by, F - fk, a=, m, where, F = applied force and f k = kinetic, friction., ● Rolling Friction Friction which comes into, play when a body like a ring or a sphere rolls, without slipping over a horizontal surface, is, known as rolling friction., 8. Angle of Friction The angle between the, resultant of limiting friction f s and normal, reaction N with the direction of N is called, angle of friction q., , Mg, , θ, Angle of repose, , 10. Centripetal Force When an object moves on, a circular path, a force acts on it, whose, direction is towards the centre of the path, this, force is called centripetal force., Centripetal force acting on a particle of mass m, on a circular path of radius r is given by, mv 2, F =, r, 11. Motion of a Car on Level Road When a car, of mass m is turning on the level road without, skidding, centripetal force on the car must be, equal or less than static friction., 2, mv max, i.e., F ³, r, 2, mv max, or, mg ³, r, (m = coefficient of friction), or, , v max £ m × rg, , \ Maximum velocity on a curved road to, avoid skidding is v max = mrg ., 12. Motion of a Car on Banked, Road Maximum velocity of a car on banked, road is given by, æ m + tan q ö, v max = rg ç, ÷, è1 - m tan q ø, where, q = inclination of road, and, r = radius of turn., If m = 0, then v = rg tan q .

Page 3 :
CBSE New Pattern ~ Physics 11th (Term-I), , 79, , Objective Questions, Multiple Choice Questions, 1. According to Galileo’s experiment for, a double inclined plane that are, smooth, when a ball is released from, rest on one of the planes rolls down and, climb up the other of decreased slope,, the final height of the ball is, (a), (b), (c), (d), , less than the initial height, more than the initial height, equal to the initial height, more or less than the initial height, , (a) bigger ball transfers greater momentum, than smaller, (b) bigger ball transfers lesser momentum than, smaller, (c) bigger ball transfer equal momentum as, smaller, (d) None of the above, , 7. A rocket is going upwards with, , explain the concept of inertia?, , accelerated motion. A man sitting in it, feels his weight increased 5 times his, own weight. If the mass of the rocket, including that of the man is 1. 0 ´ 10 4 kg,, how much force is being applied by, rocket engine? (Take, g = 10 ms -2 )., , (a) First law, (c) Third law, , (a) 5 ´ 104N, (c) 5 ´ 108 N, , 2. Which of the Newton’s laws of motion, (b) Second law, (d) All of these, , 3. If a running bus stops suddenly, our, feet stop due to friction, but the rest of, the body continues to move forward, due to, (a) momentum, , (b) force, , (c) inertia, , (d) impulse, , 4. Suppose the earth suddenly stops, attracting objects placed near surface. A, person standing on the surface of the, earth will, (a) remain standing, (c) sink into earth, , (b) fly up, (d) either (b) or (c), , 5. When a car is stationary, there is no net, force acting on it. During pick-up, it, accelerates. This happens due to, (a), (b), (c), (d), , net external force, net internal force, may be external or internal force, None of the above, , 6. A smaller and a bigger iron balls are, dropped from a small height on a glass, pane placed on a table. Only bigger, ball breakes the glass pane, because, , (b) 5 ´ 105 N, (d) 2 ´ 104N, , 8. The motion of a particle of mass m is, , described by y = ut + gt 2 , find the force, acting on the particle., (a) Zero, (c) 2 mg, , (b) mg, (d) 3 mg, , 9. A bullet of mass 0.04 kg moving with a, speed of 90 ms -1 enters a heavy, wooden block and stopped after 3s., What is the average resistive force, exerted by the block on the bullet?, (a) 1 N, (c) 2 N, , (b) 1.2 N, (d) 3 N, , 10. A body of mass 6 kg is acted on by a, force so that its velocity changes from, 3 ms -1 to 5 ms -1 , then change in, momentum is, (a) 48 N-s, (c) 30 N-s, , (b) 24 N-s, (d) 12 N-s, , 11. A meter scale is moving with uniform, velocity. This implies, , (NCERT Exemplar), , (a) the force acting on the scale is zero, but a, torque about the centre of mass can act on, the scale

Page 4 :
(b) the force acting on the scale is zero and the, torque acting about centre of mass of the, scale is also zero, (c) the total force acting on it need not be zero, but the torque on it is zero, (d) Neither the force nor the torque need to be, zero, , 12. While launching a satellite of mass, , 10 4 kg, a force of 5 ´ 10 5 N is applied for, 20s. The velocity attained by the, satellite at the end of 20s, is, (a) 4 km/s, (c) 1 km/s, , (b) 3 km/s, (d) 2 km/s, , 13. The momentum p (in kg-ms -1 ) of a, particle is varying with time t (in, second) as p = 2 + 3t 2 . The force acting, on the particle at t = 3 s will be, (a) 18 N, (c) 9 N, , (b) 54 N, (d) 15 N, , 14. A machine gun fires a bullet of mass, , 40 g with a velocity of 1200 ms -1 . The, man holding it can exert a maximum, force of 144 N on the gun., How many bullets can be fired per, second at the most?, (a), (b), (c), (d), , Only one, Three, Can fire any number of bullets, 144 ´ 48, , 15. A cricket ball of mass 150 g has an, , initial velocity u = ( 3i$ + 4$j ) ms -1 and a, final velocity v = - ( 3i$ + 4$j ) ms -1 , after, being hit. The change in momentum, (final momentum – initial momentum), is (in kgms –1 ), (NCERT Exemplar), (a) zero, (c) - (09, . $i + 12, . $j), , (b) - (045, . $i + 0.6 $j), (d) - 5($i + $j) $i, , 16. The force F acting on a particle of mass, m is indicated by the force-time graph, shown below. The change in, momentum of the particle over the time, interval from 0 to 8s is, , 6, 3, F(N), , 0, , 2, , 4, , 6, , 8, , –3, t(s), , (a) 24 N-s, (c) 12 N-s, , (b) 20 N-s, (d) 6 N-s, , 17. A particle of mass m is moving in a, straight line with momentum p. Starting, at time t = 0, a force F = kt acts in the, same direction on the moving particle, during time interval T , so that its, momentum changes from p to 3p., Here, k is a constant. The value of T is, (a), , 2p, k, , (b) 2, , p, k, , (c), , 2k, p, , (d) 2, , k, p, , 18. A constant retarding force of 50 N is, applied to a body of mass 20 kg moving, initially with a speed of 15 ms -1 . How, long time does the body take to stop?, (a) 6 s, , (b) 8 s, , (c) 9 s, , (d) 10 s, , 19. A batsman hits back at ball straight in, the direction of the bowler without, changing its initial speed of 12 ms -1 . If, the mass of the ball is 0.15 kg, find the, impulse imparted to the ball. (Assume, linear motion of the ball), (a) 1.8 N-s (b) 3.6 N-s (c) 3.6 N-m (d) 1.8 N-m, , 20. The force-time ( F -t ) graph for linear, motion of a body initially at rest is, shown in figure. The segments shown, are circular, the linear momentum, gained in 4 s is, F (N), , 2, 0, , 4, 2, , –2, , (a) 8 N-s, , 6, , 8, , t (s), , (b) 4p N-s, , (c) 2p N-s (d) 8p N-s

Page 5 :
21. Every action has an equal and opposite, reaction, which suggests that, (a) action and reaction always act on different, bodies, (b) the forces of action and reaction cancel to, each other, (c) the forces of action and reaction cannot, cancel to each other, (d) Both (a) and (c), , 22. An initially stationary device lying on a, frictionless floor explodes into two, pieces and slides across the floor. One, piece is moving in positive x-direction, then other piece is moving in, (a), (b), (c), (d), , positive y-direction, negative y- direction, negative x-direction, at angle from x-direction, , of mass 100 kg. If the muzzle speed of, the shell is 80 m/s, calculate the recoil, speed of the gun., (c) 4 m/s (d) 16 m/s, , 24. In equilibrium of particle when net, external force of the particle is zero., Then, the particle is, (a), (b), (c), (d), , and suddenly turns westward with the, same speed to avoid an opponent. The, force that acts on the player is, (NCERT Exemplar), , (a), (b), (c), (d), , frictional force along westward, muscle force along southward, frictional force along south-west, muscle force along south-west, , 28. Three concurrent coplanar forces 1 N,, 2 N and 3 N are acting along different, directions on a body can keep the body, in equilibrium, if, (a), (b), (c), (d), , 2 N and 3 N act at right angle, 1 N and 2 N act at acute angle, 1 N and 2 N act at right angle, Cannot be possible, , 29. Three blocks with masses m , 2m and 3m, , 23. A shell of mass 200 g is fired by a gun, , (a) 16 cm/s (b) 18 m/s, , 27. A hockey player is moving northward, , are connected by strings, as shown in, the figure. After an upward force F is, applied on block m, the masses move, upward at constant speed v. What is the, net force on the block of mass 2m?, (Take, g is the acceleration due to, gravity), F, m, , at rest, moving with uniform velocity, moving with uniform acceleration, Both (a) and (b), , 2m, , 25. Two forces F1 = 3 $i - 4 $j and, , 3m, , F2 = 2 $i - 3 $j are acting upon a body of, mass 2 kg. Find the force F3 , which, when acts on the body will make it, stable., (a) 5 $i + 7$j, (c) -5 $i + 7 $j, , (b) -5 $i - 7$j, (d) 5 $i - 7$j, , (a) Zero, , (b) 2 mg, , with an angle of 60° between them. If, the resultant force is equal to 40 3 N,, the magnitude of each force is, (b) 20 N, , (c) 80 N, , (d) 30 N, , (c) 3 mg, , (d) 6 mg, , 30. A ball of mass 1 kg hangs in equilibrium, from a two strings OA and OB as shown, in figure. What are the tensions in, strings OA and OB? (Take, g = 10 ms -2 ), A, , B, , 30º, , 60º, , 26. Two equals forces are acting at a point, , (a) 40 N, , v, , T1, , 90º T, 2, , 120º O 150º, , w = 10 N

Page 6 :
(a) 5 N, 5 N, (c) 5 N, 5 3 N, , (b) 5 3 N, 5 3 N, (d) 5 3 N, 5 N, , 31. Given figure is the part of a, horizontally stretched structure. Section, AB is stretched with a force of 10 N., The tension in the sections BC and BF ,, are, E, D, 120°, G, , 34. A system consists of three masses, m 1 , m 2 and m 3 connected by a string, passing over a pulley P . The mass, m 1 hangs freely and m 2 and m 3 are on a, rough horizontal table (the coefficient, of friction = m)., The pulley is frictionless and of, negligible mass. The downward, acceleration of mass m 1 is (Assume,, m1 = m 2 = m 3 = m), P, , F, , 90°, , m3, , C, B, 120°, 120°, m1, , A, , (a), (b), (c), (d), , m2, , 10 N, 11 N, 10 N, 6 N, 10 N, 10 N, Cannot be calculated due to insufficient, data, , 32. Find the force exerted by 5 kg block on, floor of lift, as shown in figure., (Take, g = 10 ms -2 ), , g (1 - gm), 9, g(1 - 2 m), (c), 3, , (a), , 2 gm, 3, g(1 - 2 m), (d), 2, , (b), , 35. Two masses m 1 = 1 kg and m 2 = 2 kg, , are connected by a light inextensible, string and suspended by means of a, weightless pulley as shown in figure., , 5 ms–2, , 2 kg, , 1 kg m1, , 5 kg, , m2 2 kg, , (a) 100 N, (c) 105 N, , (b) 115 N, (d) 135 N, , 33. Three blocks A, B and C of masses 4 kg,, 2 kg and 1 kg respectively, are in, contact on a frictionless surface, as, shown in the figure. If a force of 14 N is, applied on the 4 kg block, then the, contact force between A and B is, A, , (a) 2 N, , (b) 6 N, , B, , C, , (c) 8 N, , (d) 18 N, , Assuming that both the masses start, from rest, the distance travelled by 2 kg, mass in 2 s is, 20, m, 9, 20, (c), m, 3, , (a), , 40, m, 9, 1, (d) m, 3, , (b), , 36. If a box is lying in the compartment of, an accelerating train and box is, stationary relative to the train. What, force cause the acceleration of the box?

Page 7 :
(a) Frictional force in the direction of train, (b) Frictional force in the opposite direction of, train, (c) Force applied by air, (d) None of the above, , 37. A box of mass 2 kg is placed on the, roof of a car. The box would remain, stationary until the car attains a, maximum acceleration. Coefficient of, static friction between the box and the, roof of the car is 0.2 and g = 10 ms -2 ., The maximum acceleration of the car,, for the box to remain stationary, is, (a) 8 ms-2, (c) 4 ms-2, , (b) 6 ms-2, (d) 2 ms-2, , 38. A car of mass m starts from rest and, acquires a velocity along east,, v = v $i (v > 0 ) in two seconds. Assuming, the car moves with uniform, acceleration, the force exerted on the, (NCERT Exemplar), car is, mv, eastward and is exerted by the car, 2, engine, mv, eastward and is due to the friction on, (b), 2, the tyres exerted by the road, mv, eastward exerted due to the, (c) more than, 2, engine and overcomes the friction of the, road, mv, (d), exerted by the engine, 2, , (a), , 39. A particle of mass 2 kg is moving on a, circular path of radius 10 m with a, speed of 5 ms –1 and its speed is, increasing at a rate of 3 ms –1 . Find the, force acting on the particle., (a) 5 N, , (b) 10 N, , (c) 12 N, , (d) 14 N, , 40. Two stones of masses m and 2m are, whirled in horizontal circles, the, r, heavier one in a radius and the lighter, 2, one in a radius r. The tangential speed, , of lighter stone is n times that of the, value of heavier stone, when they, experience same centripetal forces. The, value of n is, (a) 2, , (b) 3, , (c) 4, , (d) 1, , 41. If a car is moving in uniform circular, motion, then what should be the value, of velocity of a car, so that car will not, moving away from the circle?, (a) v < m s Rg, , (b) v £ m s Rg, , (c) v < m k Rg, , (d) None of these, , 42. A person is driving a vehicle at a, , uniform speed of 5 ms -1 on a level, curved track of radius 5 m. The, coefficient of static friction between, tyres and road is 0.1. Will the person, slip while taking the turn with the same, speed? (Take, g = 10 ms -2 ), (a), (b), (c), (d), , A person will slip, if v 2 = 5 m2s-2, A person will slip, if v 2 > 5 m2s-2, A person will slip, if v 2 < 5 m2s-2, A person will not slip, if v 2 > 5 m2s-2, , 43. A circular racetrack of radius 300 m is, banked at an angle of 15°. If the, coefficient of friction between the, wheels of the race car and the road is, 0.2. Find optimum speed of the race car, to avoid wear and tear on its tyres and, maximum permissible speed to avoid, slipping. (Take, g = 9.8 ms -2 and, tan 15° = 0.27), (a), (b), (c), (d), , v o = 48 ms-1 , v max = 60 ms-1, v o = 28.1 ms-1 , v max = 38.1 ms-1, v o = 62.2 ms-1 , v max = 734, . ms-1, None of the above, , 44. A car is moving in a circular horizontal, track of radius 10.0 m with a constant, speed of 10.0 ms - 1 . A plumb bob is, suspended from the roof of the car by a, light rigid rod of length 10.0 m. The, angle made by the rod with the track is, (Take, g = 10 ms - 2 ), (a) zero, , (b) 30°, , (c) 45°, , (d) 60°

Page 8 :
45. Inertia of an object is directly, dependent on ……… ., (a) impulse, (c) mass, , (b) momentum, (d) density, , 46. A body with mass 5 kg is acted upon by, a force F = ( -3$i + 4 $j ) N. If its initial, velocity at t = 0 is u = ( 6$i - 12$j )ms -1 , the, time at which it will just have a velocity, along the Y-axis is ……… ., , (NCERT Exemplar), , (a) never, (c) 2 s, , (b) 10 s, (d) 15 s, , 47. If impulse I varies with time t as, , F (kg ms - 1 ) = 20t 2 - 20t . The change, in momentum is minimum at ……… ., , (a) t = 2s, 1, (c) t = s, 2, , (b) t = 1s, 3, (d) t = s, 2, , 48. The force which is dissipative in nature, is ……… ., (a) electrostatic force, (c) gravitational force, , (b) magnetic force, (d) frictional force, , 49. Suppose a light-weight vehicle (say, a, small car) and a heavy weight vehicle, (say, a loaded truck) are parked on a, horizontal road. Then, which of the, following statement is correct?, (a) Much greater force is needed to push the, truck., (b) Equal force is needed to push the truck and, car., (c) No force is required to move the vehicles., (d) None of the above, , 50. Which one of the following statement is, incorrect?, (a) Frictional force opposes the relative, motion., (b) Limiting value of static friction is directly, proportional to normal reaction., (c) Rolling friction is smaller than sliding, friction., (d) Coefficient of sliding friction has dimensions, of length., , 51. If no external force acts on particle,, then which of the following statement is, incorrect about particle?, (a) Particle may be at rest., (b) Particle moves with uniform velocity on, linear path., (c) Particle moves with uniform speed on circle., (d) None of the above, , 52. Match the Column I (type of friction), , with Column II (value of m) and select, the correct option from the codes given, below., Column I, , Column II, , A., , Static friction, , p., , m is highest, , B., , Rolling friction, , q., , m is moderate, , C., , Kinetic friction, , r., , m is lowest, , Codes, A, , B, , C, , A, , B, , C, , (a) r, , q, , p, , (b) p, , q, , r, , (c) p, , r, , q, , (d) q, , r, , p, , 53. In the diagram shown in figure, match, the Column I with Column II and, select the correct option from the codes, given below. (Take, g = 10 ms -2 ), F2 = 18 N, , 1 kg, 2 kg, 3 kg, , F1 = 60 N, , Smooth, , θ = 30º, , Column II, , Column I, A., , Acceleration of, 2 kg block, , p., , 8 (SI unit ), , B., , Net force on, 3 kg block, , q., , 25 (SI unit ), , C., , Normal reaction, between 2 kg, and 1 kg, , r., , 2 (SI unit ), , D., , Normal reaction, between 3 kg, and 2 kg, , s., , None

Page 9 :
Codes, A, , B, , C, , D, , (a) r, , s, , q, , s, , (b) r, , q, , s, , p, , (c) p, , q, , r, , s, , (d) p, , q, , q, , s, , Assertion-Reasoning MCQs, For question numbers 54 to 64, two, statements are given-one labelled, Assertion (A) and the other labelled, Reason (R). Select the correct answer to, these questions from the codes (a), (b), (c), and (d) are as given below, (a) Both A and R are true and R is the, correct explanation of A., (b) Both A and R are true but R is not the, correct explanation of A., (c) A is true but R is false., (d) A is false and R is also false., , 54. Assertion Aristotle stated that an, external force is required to keep a, body in motion., Reason Opposing forces are always, present in the natural world., , 55. Assertion A body is momentarily at, rest but no force is acting on it at that, time., , angle with it, it changes the component, of velocity along the direction of force., Reason The component of velocity, parallel to the force remains, unchanged., , 58. Assertion If we consider system of two, bodies A and B as a whole, F AB and F BA, are internal forces of the system, ( A + B ). They add to give a null force., Reason Internal forces in a body or a, system of particles cancel away in pairs., , 59. Assertion It is not always necessary, that external agency of force is in, contact with the object while applying, force on object., Reason A stone released from top of a, building accelerates downward due to, gravitational pull of the earth., , 60. Assertion A seasoned cricketer allows, a longer time for his hands to stop the, ball, while catching the ball. His hand is, not hurt., Reason The novice (new player) keeps, his hand fixed and tries to catch the ball, almost instantly. He needs to provide a, much greater force to stop the ball, instantly and this hurts., , Reason When a force acts on a body,, it may not have some acceleration., , 56. Assertion At the microscopic level, all, bodies are made up of charged, constituents (like nuclei and electrons), and various contact forces exist, between them., Reason These forces are due to, elasticity of bodies, molecular collisions, and impacts, etc., , 57. Assertion If force is not parallel to the, velocity of the body, but makes some, , 61. Assertion Product of distance and, velocity (i.e. momentum) is basic to the, effect of force on motion., Reason Same force for same time, causes the same change in momentum, for different bodies.

Page 10 :
62. Assertion Newton’s third law of, motion is applicable only when bodies, are in motion., Reason Newton’s third law does not, applies to all types of forces, e.g., gravitational, electric or magnetic, forces, etc., , 63. Assertion Angle of repose is equal to, angle of limiting friction., Reason When a body is just at the, point of motion, the force of friction of, this stage is called as limiting friction., , 64. Assertion A body of mass 1 kg is, making 1 rps in a circle of radius 1 m., Centrifugal force acting on it is 4 p 2 N., Reason Centrifugal force is given by, mv, ., F =, r, , Case Based MCQs, Direction Answer the questions from, 65-69 on the following case., Momentum and Newton’s Second Law of, Motion, Momentum of a body is the quantity of, motion possessed by the body. It depends on, the mass of the body and the velocity with, which it moves., When a bullet is fired by a gun, it can easily, pierce human tissue before coming to rest, resulting in casualty. The same bullet fired, with moderate speed will not cause much, damage. The greater the change in, momentum in a given time, the greater is the, force that needs to be applied., The second law of motion refers to the, general situation, where there is a net external, force rating on the body., , 65. A satellite in force-free space sweeps, stationary interplanetary dust at a rate, dM, = av , where M is the mass, v is the, dt, velocity of satellite and a is a constant., What is the deceleration of the satellite?, (a), , - 2 av 2, M, , (c) - av 2, , - av 2, M, av 2, (d), M, , (b), , 66. A body of mass 5 kg is moving with, , velocity of v = ( 2$i + 6 $j ) ms - 1 at t = 0 s., After time t = 2 s, velocity of body is, (10 $i + 6 $j ) ms -1 , then change in, momentum of body is, (a) 40 $i kg-ms -1, (b) 20$i kg-ms -1, (c) 30$i kg-ms -1, (d) (50$i + 30$j) kg-ms -1, , 67. A cricket ball of mass 0.25 kg with, speed 10 m/s collides with a bat and, returns with same speed with in 0.01s., The force acted on bat is, (a) 25 N, (c) 250N, , (b) 50N, (d) 500N, , 68. A stationary bomb explodes into three, pieces. One piece of 2 kg mass moves, with a velocity of 8 ms -1 at right angles, to the other piece of mass 1 kg moving, with a velocity of 12 ms -1 . If the mass of, the third piece is 0.5 kg, then its, velocity is, (a) 10 m s-1, (c) 30 m s-1, , (b) 20 ms-1, (d) 40 ms-1, , 69. A force of 10 N acts on a body of mass, 0.5 kg for 0.25s starting from rest. What, is its momentum now?, (a) 0.25 N/s, (c) 0.5 N/s, , (b) 2.5 N/s, (d) 0.75 N/s

Page 11 :
2T . Then, the velocity acquired by the, body is, , Direction Answer the questions from, 70-74 on the following case., Conservation of Momentum, This principle is a consequence of Newton’s, second and third laws of motion., In an isolated system (i.e. a system having no, external force), mutual forces (called internal, forces) between pairs of particles in the, system causes momentum change in, individual particles., Let a bomb be at rest, then its momentum will, be zero. If the bomb explodes into two equal, parts, then the parts fly off in exactly opposite, directions with same speed, so that the total, momentum is still zero. Here, no external, force is applied on the system of particles, (bomb)., , 74. Two masses of M and 4M are moving, , 70. A bullet of mass 10 g is fired from a gun, , with equal kinetic energy. The ratio of, their linear momenta is, , of mass 1 kg with recoil velocity of gun, 5 m/s. The muzzle velocity will be, (a), (b), (c), (d), , 30 km/min, 60 km/min, 30 m/s, 500 m/s, , 0, , A, T, , B, 2T, , – F0, , p F0 T, 4m, F0 T, (c), 4m, , (a), , (b), , p F0 T, 2m, , (d) zero, , (a) 1 :8, (c) 1 :2, , (b) 1 :4, (d) 4 :1, , Direction Answer the questions from, 75-79 on the following case., , 71. A shell of mass 10 kg is moving with a, , velocity of 10 ms - 1 when it blasts and, forms two parts of mass 9 kg and 1 kg, respectively. If the first mass is, stationary, the velocity of the second is, (a), (b), (c), (d), , F0, , 1 m s -1, 10 m s-1, 100 m s-1, 1000 m s-1, , Force of Friction on Connected Bodies, When bodies are in contact, there are mutual, contact forces satisfying the third law of, motion. The component of contact force, normal to the surfaces in contact is called, normal reaction. The component parallel to, the surfaces in contact is called friction., , 72. A bullet of mass 0.1 kg is fired with a, , speed of 100 ms -1 . The mass of gun, being 50 kg, then the velocity of recoil, becomes, (a) 0.05 m s-1, (c) 0.1 m s-1, , (b) 0.5 m s-1, (d) 0.2 m s-1, , 73. A unidirectional force F varying with, time T as shown in the figure acts on a, body initially at rest for a short duration, , 8 kg, , 6 kg, , In the above figure, 8 kg and 6 kg are hanging, stationary from a rough pulley and are about, to move. They are stationary due to, roughness of the pulley.

Page 12 :
75. Which force is acting between pulley, and rope?, (a), (b), (c), (d), , Gravitational force, Tension force, Frictional force, Buoyant force, , 78. The force of friction acting on the rope, is, (a) 20 N, (c) 40 N, , 76. The normal reaction acting on the, system is, (a) 8 g, (c) 2 g, , (a) 8 kg, (b) 6 kg, (c) Same on both, (d) Nothing can be said, , (b) 6 g, (d) 14 g, , (b) 30 N, (d) 50 N, , 79. Coefficient of friction of the pulley is, 1, 6, 1, (c), 5, , 1, 7, 1, (d), 4, , (a), , 77. The tension is more on side having, mass of, , (b), , ANSWERS, Multiple Choice Questions, 1. (c), 11. (b), 21. (d), 31. (c), , 2. (a), 12. (c), 22. (c), 32. (c), , 3. (c), 13. (a), 23. (a), 33. (b), , 4. (a), 14. (b), 24. (d), 34. (c), , 5. (a), 15. (c), 25. (c), 35. (c), , 6. (a), 16. (c), 26. (a), 36. (a), , 7. (b), 17. (b), 27. (c), 37. (d), , 8. (c), 18. (a), 28. (d), 38. (b), , 9. (b), 19. (b), 29. (a), 39. (a), , 10. (d), 20. (c), 30. (c), 40. (a), , 41. (b), 51. (c), , 42. (b), 52. (c), , 43. (b), 53. (a), , 44. (c), , 45. (c), , 46. (b), , 47. (c), , 48. (d), , 49. (a), , 50. (d), , 56. (a), , 57. (c), , 58. (c), , 59. (c), , 60. (b), , 61. (d), , 62. (d), , 63. (a), , 67. (d), 77. (a), , 68. (d), 78. (a), , 69. (b), 79. (b), , 70. (d), , 71. (c), , 72. (d), , 73. (d), , 74. (c), , Assertion-Reasoning MCQs, 54. (a), 64. (c), , 55. (d), , Case Based MCQs, 65. (d), 75. (c), , 66. (a), 76. (d)

Page 13 :
CBSE New Pattern ~ Physics 11th (Term-I), , 89, , SOLUTIONS, 1. Galileo conducted an experiment using a, double inclined plane. In this experiment,, two inclined planes are arranged facing each, other., When an object rolls down one of the, inclined planes, it climbs up the other. It, almost reaches the same height but not, completely because of friction. In ideal case,, when there is no friction the final height of, the object is same as the initial height as, shown in figure., Initial, position, , Final, position, , Both planes are inclined at same angle, , 2. According to Newton’s first law of motion,, everybody continues in its state of rest or, uniform motion. Unless an external force acts, upon it. This depicts that a body by itself, cannot change its state of rest or of uniform, motion along a straight line., This law is known as law of inertia., , 3. This is because the feet of the passenger, comes to rest along with the bus, but the, upper part of his body, due to inertia of, motion, tends to remain in motion., , 4. If downward force on the earth stops, so, upward self-adjusting force also stop. In, vertical direction, there is no force. Due to, inertia, person resists any change to its state, of rest. So, person will remain standing., 5. During pick-up, the car accelerates. This must, happens due to a net external force. This is, because, the acceleration of the car cannot be, accounted for by any internal force. The only, conceivable external force along the road is, the force of friction. It is the frictional force, that accelerates the car as a whole., 6. Since, momentum is directly proportional to, mass of the body. Hence, when both iron, balls are dropped from same height, then, bigger ball gain greater momentum than, smaller ball at the time of striking the glass, pane. Hence, it can transfer greater, , momentum to the glass pane and so it, breaks., , 7. Given, m = 1.0 ´ 10 4 kg, As the weight of the man is increased, 5 times, so acceleration of the rocket, also, increase to 5 times., i.e., a = 5g = 5 ´ 10 = 50 ms -2, Force applied by rocket engine,, F = ma = 1.0 ´ 10 4 ´ 50 = 5 ´ 10 5 N, 1, 2, , 8. From equation of motion, y = ut + at 2, where, a is the acceleration., , …(i), , 1, × 2gt 2 …(ii), 2, Comparing Eqs. (i) and (ii), we get, Acceleration, a = 2 g, Force = m ´ a = m × 2g = 2mg, , Given equation, y = ut + gt 2 = ut +, , 9. Given, mass of bullet, m = 0.04 kg, Initial speed of bullet, u = 90 ms -1, Time, t = 3 s, Final velocity of bullet, v = 0, If a be the retardation in the bullet in the, wooden block, then, From equation of motion, v = u - at, 0 = 90 - a ´ 3, Þ, 3a = 90 Þ a = 30 m/s 2, \ Average resistive force,, F = m × a = 0.04 ´ 30 = 1.2 N, 10. Given, mass, m = 6 kg, Velocity, v = v 2 - v 1 = 5 - 3 = 2, \ Momentum, p = mv = 6 ´ 2 = 12 N-s, , 11. To solve this question we have to apply, Newton’s second law of motion, in terms of, force and change in momentum., dp, We know that, F =, dt, Given that, meter scale is moving with, uniform velocity, hence dp = 0., Force, F = 0., As all parts of the scale is moving with, uniform velocity and total force is zero,, hence torque will also be zero.

Page 14 :
16. The area under F-t graph gives change in, , 12. Given, mass of satellite, m = 10 4 kg, F = 5 ´ 10 N, t = 20 s, u = 0, v = ?, Impulse applied on the satellite is equal to, the change in momentum., i.e., F × t = m (v - u ), 5 ´ 10 5 ´ 20 = 10 4 ( v - 0 ), 5, , Þ, , v =, , 5 ´ 10 5 ´ 20, = 1000 m/s = 1 km/s, 10 4, , momentum., So, for the F-t graph as shown below, , F(N) 0, A 2, , –3, , F, , 4, D, , I, , 6, 8, t(s), E, , 1, ´ 2 ´ 6 = 6 kg-ms -1, 2, For 2 to 4s, Dp 2 = Area under the rectangle, CFEDC, = 2 ´ -3 = - 6 kg-ms -1, For 4 to 8s, Dp 3 = Area under the rectangle, , =, , \ Force acting on the particle = 18 N, Dp ö, ÷, è Dt ø, , 14. From Newton’s second law, F = n × æç, , where, F = force, n = number of bullets fired, Dp, per second and, = rate of change of, Dt, momentum of one bullet., æmv - 0 ö, Þ, F =n ç, ÷, è Dt ø, Given, F = 144 N, m = 40 g = 40 ´ 10-3 kg,, v = 1200 ms-1 and Dt = 1 s, 40 ´ 10 - 3 ´ 1200, \, 144 = n ´, 1, 144, Þ, n=, 4 ´ 12, n=3, , 15. Given, u = ( 3$i + 4 $j ) m/s, and v = - ( 3i$ + 4 $j ) m/s, Mass of the ball, m = 150 g = 0.15 kg, Dp = Change in momentum, = Final momentum – Initial momentum, = mv - mu, = m ( v - u ) = ( 015, . ) [-( 3i$ + 4 $j ) - ( 3$i + 4 $j )], = ( 015, . ) [ -6 $i - 8 $j ], , Hence, Dp = - [ 0. 9 i$ + 1 . 2$j ], , C, , H, , For 0 to 2s, Dp 1 = Area under the triangle ABC, , Differentiate w.r.t. t, we get, dp, = 0 + 3 ´ 2t = 6t, dt, dp, If t = 3 s, then, = 6 ´ 3 = 18 N, dt, , = - [ 015, . ´ 6 i$ + 015, . ´ 8 $j ], = - [ 0. 9 i$ + 1. 20 $j ], , G, , 3, , 13. Given, p = 2 + 3t 2, , Þ, , B, , 6, , FIHGF, = 4 ´ 3 = 12 kg-ms -1, So, total change in momentum for 0 to 8s,, Dp net = Dp 1 + Dp 2 + Dp 3, = ( + 6 - 6 + 12) = 12 kgms -1 = 12 N-s, , 17. Here, F = kt, When t = 0, then linear momentum = p, When t = T , then linear momentum = 3p, According to Newton’s second law of motion,, dp, Applied force, F =, dt, or, dp = F × dt, or, dp = kt × dt, Now, integrate both side with proper limit, 3p, , T, , T, , ét2 ù, 3p, or, dp, k, t, dt, =, [, p, ], =, k, p, ê 2ú, òp, ò0, ë û0, 1, 2, or ( 3 p - p ) = k (T - 0 ), 2, 4p, p, or, or T = 2, T2=, k, k, , 18. Given, F = 50 N, m = 20 kg, v = 15 ms -1, mv, Dt, mv, Dt =, F, 20 ´ 15, Dt =, =6 s, 50, , Impulse, F =, Time,

Page 15 :
19. The situation is as depicted below, , 24. In equilibrium, net force is zero, therefore, acceleration is zero, hence particle is either at, rest or in motion with uniform velocity., , 25. For stable condition,, m= 0.15 kg, , Initial momentum = mv = 0 .15 ´ 12, = 18, . N-s to right, Final momentum = mv = 0.15 ´ 12, = 1.8 N-s to left, Impulse = Change in momentum, = Final momentum - Initial momentum, = (1.8 N-s ) - ( - 1.8 N-s ), = (1.8 N-s ) + (1.8 N-s ) = 3.6 N-s, = 3.6 N-s towards left, , 20. According to figure, radius of semi-circle,, r =2, Linear momentum gained, = Impulse from 0 to 4 s, = Area enclosed by graph from 0 to 4 s, pr 2 p ( 2) 2, =, =, = 2p N-s, 2, 2, , F1 + F2 + F3 = 0, ( 3$i - 4 $j) + ( 2$i - 3$j) + F3 = 0, Þ, F = -5 $i + 7 $j, , (given), , 3, , 26. Let equal forces F 1 = F 2 = F newton, Angle between the forces, q = 60°, Resultant force, R = 40 3 N, Now, R = F 12 + F 22 + 2F 1 F 2 cos q, \ 40 3 = F 2 + F 2 + 2FF cos 60°, or, , F = 40 N, , 27. Consider the adjacent diagram, N, B, , A, , W, , E, , O, , 21. Action and reaction forces always act on, different bodies, because if they work on, same body, then net force on the body is, zero and there could never be accelerated, motion., So, they cannot balance or cancel each other., , S, , Let, OA = p 1, = initial momentum of player northward, and AB = p 2 = final momentum of player, towards west., , Hence, options (a) and (c) are correct., , B, , A, , R, , O, , 22. From law of conservation of momentum,, pi = p f, and initial momentum, p i = mu = m ( 0 ) = 0, \ p f should also be zero., Hence, other piece will move in negative, x-direction., , 23. From conservation of linear momentum,, m 2v 2 = m 1v 1, 200, 100 v 2 =, ´ 80, 1000, 200 ´ 80, v2 =, 1000 ´ 100, Þ, or, , v 2 = 0.16 m/s, v 2 = 16 cm/s, , Clearly,, OB = OA + AB, Change in momentum = p 2 - p 1, = AB - OA = AB + ( - OA ), = Clearly resultant AR will be along, , south-west., 28. From the given forces, we can say that first, two forces 1 N and 2 N, if are in the same, direction, then it would be equal to third, force 3 N. But it is given that, all the three, forces are in different directions., So, there is no possibility that these three, forces, are in equilibrium.

Page 16 :
29. Since, all the blocks are moving with constant, , 32., , N, , velocity and we know that, if velocity is, constant, acceleration of the body becomes, zero., Hence, the net force on all the blocks will be, zero., , 2 kg, , 70 N, , 30. Apply Lami’s theorem at O,, , N - 70 = 7 ´ 5, , T1, T2, =, sin 150° sin 120°, 10, 10, =, =, = 10, sin 90° 1, \, , –2, , 5 ms, , 5 kg, , \, , N = 105 N, m A = 4 kg,, , 33. Given,, , m B = 2 kg, m C = 1 kg and F = 14 N, , T 1 = 10 sin 150°, 1, = 10 ´ = 5 N, 2, T 2 = 10 sin 120°, 3, = 10 ´, =5 3N, 2, , a, F, , 31. T 1 and T 2 are the tensions in the sections BC, and BF , then resolution of all forces at B in, two perpendicular directions are shown, below, , A, , B, , C, , So, total mass, M = 4 + 2 + 1 = 7 kg, Now, F = Ma Þ 14 = 7a Þ a = 2 ms -2, FBD of block A,, a, F, , F′, , 4 kg, , T1 sin 30°, C, , T2 sin 30°, T1, B, , 30°, T1 cos 30°, , 90°, , 30°, 90°, , F, , T2, T2 cos 30°, , Þ F ¢ = F - 4a = 14 - 4 ´ 2 Þ F ¢ = 6 N, Hence, the contact force between A and, B is 6 N., , 34. First of all consider the forces on the blocks, as shown below, , a, , 10 N, T1, , A, , For equilibrium along horizontal direction,, T 1 cos 30° = T 2 cos 30°, Let,, T1 =T2 =T, Again, for equilibrium along vertical, direction., T 1 sin 30° + T 2 sin 30° = 10, Þ, 2T sin 30° = 10, 1, 2T ´ = 10 Þ T = 10 N, 2, So, the tension in both sections BC and, BF is 10 N., , m, , T2 T3, , µmg, , a T1, m, , 2, , 3, , m, µmg, , 1, , mg, , For the Ist block, mg - T 1 = m ´ a, …(i), Let us consider 2nd and 3rd blocks as a system,, so, …(ii), T 1 - 2 mmg = 2m ´ a, Adding Eqs. (i) and (ii), we get, g, mg (1 - 2 m ) = 3m ´ a Þ a = (1 - 2 m ), 3

Page 17 :
35. Given, m 1 = 1 kg , m 2 = 2 kg and g = 10 ms -2, æm - m 1 ö, Acceleration, a = ç 2, ÷g, èm 1 + m 2 ø, æ 2 -1ö, 10, =ç, ÷ 10 =, è1 + 2 ø, 3, 1 2, é, -1 ù, êëQ s = ut + 2 at and u = 0 ms úû, 1, Distance, s = ´ a ´ t 2, 2, 1 10, 20, = ´ ´4=, m, 2 3, 3, , 36. Frictional force in the direction of train, causes the acceleration of the box lying in, the compartment of an accelerating train., , 37. Given, m = 2 kg, m = 0 . 2, and, g = 10 m/s2, Here, ma = mmg, Þ, a = mg = 0.2 ´ 10 = 2 ms-2, , 38. Given, mass of the car = m, As car starts from rest, u = 0, Velocity acquired along east = v $i, Duration, t = 2s., We know that, v = u + at, Þ, v $i = 0 + a ´ 2, Þ, Force,, , a=, , v$, i, 2, , F = ma =, , mv $, i, 2, , mv, towards, 2, east. As external force on the system is only, mv, is by friction., friction, hence the force, 2, Hence, force by engine is internal force., , Hence, force acting on the car is, , 39. Given, m = 2 kg, r = 10 m and v = 5 ms -1, Radial acceleration (centripetal acceleration), v2 5 ´ 5, =, =, = 2.5 ms -2, r, 10, Force = Mass ´ Acceleration = 2 ´ 2.5 = 5 N, , 40. Given that, two stones of masses m and 2m, are whirled in horizontal circles, the heavier, , one in a radius r / 2 and lighter one in, radius r., As, lighter stone is n times that of the value of, heavier stone when they experience same, centripetal forces, we get, ( F c ) heavier = ( F c ) lighter, 2m ( v ) 2 m (nv ) 2, Þ, =, ( r / 2), r, Þ, Þ, , n2 = 4, n=2, , 41. For car moving in circle of radius R, with, velocity v and mass = m ,, Centripetal force required, = Frictional force £ m s N, mv 2, (Q N = mg ), £ m smg, R, v £ m s Rg, , 42. We know that, F =, , 2, mv max, r, , …(i), , and, …(ii), F = m smg, From Eqs. (i) and (ii) for maximum speed of, vehicle, mv 2, m smg ³ max, r, where, v max = maximum velocity of vehicle., Given, m s = 01, . , r = 5 m and g = 10 ms -2, \, v max = m s rg, 2, v max, = 01, . ´ 5 ´ 10 = 5 m 2 s -2, So, person or vehicle will slip, if v 2 > 5 m 2 s -2 ., , 43. Given, m s = 0.2, R = 300 m and q = 15°, Optimum speed, v o = gR tan q, = 9.8 ´ 300 ´ tan 15°, = 2940 ´ 0.27 = 28.1 ms -1, and v max =, =, , gR ( m s + tan 15° ), 1 - m s tan 15°, 9.8 ´ 300 (0.2 + 0.27), 1 - 0.2 (0.27), , = 38.1 ms -1, Thus, the optimum speed and maximum, permissible speed are 28.1 ms -1 and, 38.1 ms -1 , respectively.

Page 18 :
44. If angle of banking is q, then, tan q =, , 2, , 50. The opposing force that comes into play, when one body is actually sliding over the, surface of the other body is called sliding, friction., , 2, , mv /r, v, Þ tan q =, mg, rg, , Given, v = 10 ms -1, r = 10 m, and g = 10 ms- 2, (10 ) 2, So, tan q =, =1, 10 ´ 10, , The coefficient of sliding is given as, m S = N / F sliding, where, N is the normal reaction and F sliding is, the sliding force., As, the dimensions of N and F sliding are same., Thus, m S is a dimensionless quantity. When, body is rolling, then it reduces the area of, contact of surfaces, hence rolling friction is, smaller than sliding friction., , \, q = 45°, 45. The term inertia means resistance of any, physical object. It is defined as the tendency, of a body to remain in its position of rest or, uniform motion. So, it is dependent on mass, of the body., , 46. Given, mass, m = 5 kg, , Hence, statement (d) is incorrect., , 51. When particle moves in a circle even with, , Acting force, F = ( -3$i + 4 $j ) N, Initial velocity at t = 0, u = ( 6 $i - 12$j ) m/s, Retardation, a$ =, , F æ 3i$ 4 $j ö, = ç+, ÷ m/s 2, m è 5, 5ø, , As final velocity is along Y-axis only, its, x-component must be zero., From v = u + at, for x-component only,, 3$i, 0 = 6 $i - t, 5, 5´6, t=, = 10 s, 3, , 47. Impulse is defined as rate of change of, momentum. For change in momentum to be, minimum., d, ( 20t 2 - 20t ) = 0, dt, 40t - 20 = 0, 1, t= s, 2, , 48. Frictional force is a non-conservative force, because work done by it is dissipated, (wasted) as heat energy. This is not the case, with other forces., , 49. Due to inertia, greater force is needed to, push the truck than the car, to bring them to, the same speed in same time., Thus, the statement given in option (a) is, correct, rest are incorrect., , 52., , uniform or constant speed, it faces an, external force towards its centre called, centripetal force. Hence, the statement given, in option (c) is incorrect., A. Static friction is the frictional force, between the surfaces of two objects when, they are not in motion with respect to each, other., Due to this reason, static friction has the, highest value of frictional force and hence, m is highest., B. Rolling friction takes place when one body, rolls over the surface of another body due, to which the value of friction is less in case, of rolling friction and hence m is lowest., C. Kinetic friction takes place when one body, slides over the surface of the another body., Value of friction is moderate and lie in, between the friction value of rolling and, static friction and hence m is moderate., Hence, A ® p, B ® r and C ® q., , 53. Acceleration of system,, a =, , 60 - 18 - (m 1 + m 2 + m 3 ) g sin 30°, = 2 ms -2, (m 1 + m 2 + m 3 ), , Net force on 3 kg block = m 3a = 6 N, From free body diagram of 3 kg block, we, have, N 12 - m 1 g sin 30° - 18 = m 1 a, Þ, N 12 = 25 N, From free body diagram of 3 kg block, we, have

Page 19 :
60 - m 3 g sin 30° - N 32 = m 3a, \, , N 32 = 39 N, , Hence, A ® r, B ® s, C ® q and D ® s., , 54. Aristotle stated that an external force is, required to keep a body in motion as it can, be observed in our surrounding, i.e. to move, a body, we need to push or pull an object., But Aristotle didn’t give any reason behind, this fact., The reason behind this fact is that, there are, number of opposing forces like friction,, viscosity, etc., are always present in the, natural world. To counter these opposing, forces, some external force is required to, keep a body in motion., Therefore, both A and R are true and R is, the correct explanation of A., , 55. A stationary body ( v = 0 ) may still have some, acceleration, e.g. when a body is thrown in, upward direction, it comes to rest at highest, position, but at that time, it still have, acceleration equal to acceleration due to, gravity g ., Hence, gravitational force is acting at highest, position and when a force acts on a body,, then its accelerates., Therefore, A is false and R is also false., , 56. At the microscopic level, all bodies are made, up of charged constituents and various, contact forces exist between them., These forces are due to elasticity of bodies,, molecular collisions and impacts etc., Therefore, both A and R are true and R is, the correct explanation of A., , 57. Force is a vector quantity. Thus, if force is, not parallel to the velocity of the body, but, makes some angle with it, it changes the, component of velocity along the direction of, force., The component of velocity normal to the, force remains unchanged, e.g. in projectile, motion, horizontal component of velocity, does not change under the effect of vertical, gravitational force., Therefore, A is true but R is false., , 58. If force on A by B = FAB and force on B by, A = FBA ., These forces add to give a null force when, FAB = – FBA ., Here FAB and FBA are internal forces of ( A + B ), system., Internal forces in a body do not cancel away,, as they do not act on the same particle., Therefore, A is true but R is false., , 59. It is not always necessary that external, agency of force is in contact with the object,, while applying force on object., Force can be applied on a body/particle, without contact or with contact, it depends, on the agency, applying force. e.g., earth pulls (exerts force) from distance., A stone without any physical contact falls, due to gravitational pull of the earth., Therefore, A is true but R is false., Change in momentum Dp, 60. Force =, =, Time interval, Dt, If time interval is increased, then force will, get decreased (for constant Dp). Therefore,, reaction force on the hand is small, i.e. he, experience less hurt., This is what seasoned cricketer does., New player make Dt small, so force is more,, which hurt new player’s hand., Therefore, both A and R are true but R is, not the correct explanation of A., , 61. As we know, momentum, p = mv, Change in p can be brought by changing, force F i.e., dp, F=, = rate of change of momentum with, dt, time., Þ, md v = Fdt, So, in order to keep, Fdt constant, mdv should, be constant, here m and dv can change from, one body to another body., Thus, same force for same time can cause, different change in momentum for different, bodies., Therefore, A is false and R is also false.

Page 20 :
62. According to Newton’s third law of motion, it, is impossible to have a single force out of, mutual interaction between two bodies,, whether they are moving or at rest., It means, third law of motion is applicable to, all the bodies either at rest or in motion and, this law is also applicable to all types of, forces., Therefore, A is false and R is also false., , 63. Angle of repose is equal to angle of limiting, friction and maximum value of static friction, is called the limiting friction., Maximum force of static friction which, comes into play when a body just starts, moving. Over the surface of another body is, called limiting friction., Therefore, both A and R are true and R is, the correct explanation of A., , 64. From relation, the centrifugal force,, mv 2 m ( r w ) 2, =, = mrw2, r, r, = mr ( 2pn ) 2 = 4 p 2 mr n 2, = 4 p 2 ´ 1 ´ 1 ´ 12 = 4 p 2 N, mv 2, Centripetal force, F =, r, , F =, , Therefore, A is true but R is false., dp, é dM ù, 65. Force, F =, =v ê, = av 2, dt, ë dt úû, Þ, , a =, , F, av 2, =, M, M, , 66. Given, mass, m = 5 kg, Change in velocity, Dv =, v f - v i = [(10 - 2) i$ + ( 6 - 6 ) $j ], Change in momentum, = mDv = 5 [8 $i ] = 40 $i kg -ms - 1, , 67. Momentum,, Dp = 2mv = 2 ´ 0.25 ´ 10 = 5 kg-m/s, Dp, 5, Force, F =, =, = 500 N, Dt, 0.01, , 68. Momentum of third piece,, p=, , p x2 + p 2y = (16 ) 2 + (12) 2, , = 20 kg-m/s, , v =, , p 20, =, = 40 m/s, m 0.5, px = 2×8 = 16, , py = 1×12 = 12, , 69. Given, F = 10 N, v i = 0,, m = 0.5 kg, Dt = 0 .25 s, Q Change in momentum, Dp = p f - p i, Also, Dp = F × Dt, From Eqs. (i) and (ii), we get, F × Dt = p f - p i, or 10 ´ 0.25 = p f - mv i, 2.5 = p f - 0.5 ´ 0, Þ, p f = 2.5 N/s, , …(i), …(ii), , 70. Conservation of linear momentum gives, m 1v 1 + m 2v 2 = 0, m 1v 1 = - m 2v 2, - m 2v 2, v1 =, Þ, m1, æ 10 ö, Given, m 1 = 10 g = ç, ÷ kg, è1000 ø, m 2 = 1 kg and v 2 = -5 m/s, \ Velocity of muzzle,, +1´ 5, v1 =, = 500 m/s, 10 /1000, , 71. Given that, v 1 = 10 m s -1,, m 1 = 10 kg, v 2 = 0 ,, m 2 = 9 kg, v 3 = v ,, m 3 = 1 kg, According to conservation of momentum,, m 1v 1 = m 2v 2 + m 3v 3, 10 ´ 10 = 9 ´ 0 + 1 ´ v Þ v = 100 ms -1, , 72. From the law of conservation of momentum,, Initial momentum = Final momentum, Þ m 1u1 + m 2u2 = m 1v 1 + m 2v 2, \ 0.1 ´ 0 + 50 ´ 0 = 0.1 ´ 100 + 50 (- v 2 ), Þ, 0 = 10 - 50v 2, 10, v2 =, \, = 0.2 ms -1, 50

Page 21 :
73. From 0 to T , area is positive and from T to, , 77. As, tension, T = mg Þ T µ m, , 2T , area is negative, so net area is zero., Hence, there is no change in momentum., , 74. Two masses are moving with equal kinetic, energy., 1, 1, M v 12 = 4 M v 22, 2, 2, v1, or, =2, v2, The ratio of linear momentum is, p1, M v1, =, p2 4 M v 2, or, , p1 1 æ v 1 ö, = ç ÷, p2 4 è v 2 ø, , or, , p1 2 1, = =, p2 4 2, , Þ, , p1 : p2 = 1 : 2, , 75. Frictional force acts between pulley and rope., 76. The reaction force is, R = T 1 + T 2 = ( 8 + 6 ) g = 14 g, , So, the side having 8 kg mass will have more, tension., , 78., f (force of friction), , T2, T1, , 6 kg, , 8 kg, , Due to friction, tension at all points of the, thread is not alike., T 1 -T 2 = f, Þ, f = 8 g -6 g = 2g, (Q g = 10 ms -2 ), = 20 N, , 79. As, mR = f = 20 N, m=, , 20, 20, 1, =, =, R 14 ´ 10 7, , (Q R = mg )