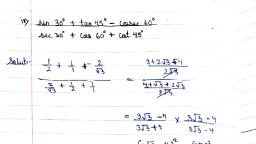Page 1 :
Trigonometrical Ratios, Functions and Identities 1, , Chapter, , 1, , CONTENTS, 1.1, , Definitions, , 1.2, , Systems of Measurement of Angles, , 1.3, , Relation between Three Systems of Measurement, of an Angle, , 1.4, , Relation between an Arc and an Angle, , 1.5, , Trigonometrical Ratios or Functions, , 1.6, , Trigonometrical Ratios of Allied Angles, , 1.7, , Trigonometrical Ratios for Various Angles, , 1.8, , Trigonometrical Ratios in terms of each other, , 1.9, , Trigonometrical Ratios of Sum and Difference of, , The study of trigonometry was first started in, , Two Angles, 1.10, , The Great Indian Mathematician Aryabhatta, , Trigonometrical Ratios of Sum and Difference of, Three Angles, , India. The ancient Indian Mathematicians,, Aryabhatta (476 A.D.), Bhaskara I (600 A.D.), and Bhaskara (1114 A.D.) and Brahmagupta, (598 A.D.) got important results. All this, knowledge first went from India to middle-east, and from there to Europe. The Greeks has also, started the study of trigonometry but their, approach was so clumsy that when the Indian, approach became known, it was immediately, adopted throughout the world., , 1.11, , Transform the Product into Sum or Difference, , 1.12, , Trigonometrical Ratios of multiple of an Angle, , 1.13, , Trigonometrical Ratios of sub multiple of an Angle, , 1.14, , Maximum and Minimum value of a cos + b sin, , 1.15, , Conditional Trigonometrical Identities, , Bhaskara I (about 600 A.D.) gave formulae to, , Assignment (Basic and Advance Level), , find the values of sine function for angles more, than 90o. A sixteenth century Malayalam work, Yuktibhasa (period) contains a proof for the, expansion of sin (A+B). Exact expressions for, sines or cosines of 18o, 36o, 54o, 72o, etc. are, given by Bhaskara II., , Answer Sheet

Page 2 :
2 Trigonometrical Ratios, Functions and Identities, , 1.1 Definitions., (1) Angle : The motion of any revolving line in a plane from its initial position (initial side) to, the final position (terminal side) is called angle. The end point O about, which the line rotates is called the vertex of the angle., , B, Terminal, side, , (2) Measure of an angle : The measure of an angle is the amount of, , O, , rotation from the initial side to the terminal side., , Initial side, , A, , (3) Sense of an angle : The sense of an angle is determined by the, direction of rotation of the initial side into the terminal side. The sense of an angle is said to be, positive or negative according as the initial side rotates in anticlockwise or clockwise direction, to get the terminal side., B, , O, , , Positive, angle, , O, , A, , , , A, , B Negative, angle, , (4) Right angle : If the revolving ray starting from its initial position to final position, describes one quarter of a circle. Then we say that the measure of the angle formed is a right, angle., (5) Quadrants : Let X ' OX and YOY ' be two lines at right angles in the plane of the paper., These lines divide the plane of paper into four equal parts. Which are, Y, known as quadrants. The lines X ' OX and YOY ' are known as x-axis, and y-axis. These two lines taken together are known as the coII, I, quadrant, quadrant, ordinate axes., (6) Angle in standard position : An angle is said to be in standard, position if its vertex concides with the origin O and the initial side, concides with OX i.e., the positive direction of x-axis., , X, , X, , O, , III, quadrant, , IV, quadrant, , Y, , (7) Angle in a quadrant : An angle is said to be in a particular, quadrant if the terminal side of the angle in standard position lies in that quadrant., , (8) Quadrant angle : An angle is said to be a quadrant angle if the terminal side concides with, one of the axes., , 1.2 System of Measurement of Angles, There are three system for measuring angles

Page 3 :
Trigonometrical Ratios, Functions and Identities 3, , (1) Sexagesimal or English system : Here a right angle is divided into 90 equal parts known as, degrees. Each degree is divided into 60 equal parts called minutes and each minute is further, 1 right angle = 90 degree ( 90 o ), , divided into 60 equal parts called seconds. Therefore,, , 1o  60 minutes ( 60 ' ), 1'  60 second ( 60 ' ' ), (2) Centesimal or French system : It is also known as French system, here a right angle is, divided into 100 equal parts called grades and each grade is divided into 100 equal parts, called, minutes and each minute is further divided into 100 seconds. Therefore,, 1 right angle = 100 grades ( 100 g ), 1 grade = 100 minutes ( 100 ' ), 1 minute = 100 seconds ( 100 ' ' ), (3) Circular system : In this system the unit of measurement is radian. One radian, written as, c, , 1 , is the measure of an angle subtended at the centre of a circle by an arc of length equal to the, radius of the circle., P, O, , A, , Consider a circle of radius r having centre at O. Let A be a point on the circle. Now cut off, an arc AP whose length is equal to the radius r of the circle. Then by the definition the measure, of AOP is 1 radian ( 1c ) ., , 1.3 Relation between Three Systems of Measurement of an Angle., Let D be the number of degrees, R be the number of radians and G be the number of grades, in an angle ., Now,, , 90 o = 1 right angle, , , , Do , , D, right angles, 90, ,  1o , , 1, right angle, 90,  , , D, right angles, 90, , ……..(i), Again,, , ……..(ii), ,  radians = 2 right angles, R radians , , 2R, , , , right angles, ,  1 radian ,  , , 2R, , , , 2, , , , right angles, , right angles

Page 4 :
4 Trigonometrical Ratios, Functions and Identities, and, , 100 grades = 1 right angle, , , , G grades , ,  1 grade , , G, right angles, 100, ,  , , 1, right angle, 100, , G, right angles, 100, , ……..(iii), , D, G, 2R, , , 90 100, π, , From (i), (ii) and (iii) we get,, , This is the required relation between the three systems of measurement of an angle., , Note, , :  One radian , , 180 o, , , ,   radians  180 o  1 radian = 57o 1 7 44 .8   57 o1 7 4 5  ., , 1.4 Relation between an Arc and an Angle., If s is the length of an arc of a circle of radius r, then the angle  (in radians) subtended by, this arc at the centre of the circle is given by  , , s, or s  rθ i.e., arc = radius, r, , × angle in radians, , B, , , O, , C, , r, , s, A, , Sectorial area : Let OAB be a sector having central angle  C and radius r., Then area of the sector OAB is given by, , 1 2, r θ., 2, Important Tips, ,  The angle between two consecutive digits in a clock is 30o (= /6 radians). The hour hand rotates through an angle, of 30o in one hour., , , The minute hand rotate through an angle of 6o in one minute., , Example: 1, , The circular wire of radius 7 cm is cut and bend again into an arc of a circle of radius 12 cm. The, angle subtended by an arc at the centre of the circle is, [Kerala (Engg.) 2002], (a) 50 o, , Solution: (b), , Given the diameter of circular wire = 14 cm. Therefore length of wire = 14  cm, Hence, required angle , , Example: 2, , (b) 22o, , (c) 23o, , c, , (d) 24o, , We have,  radians  180 o, o, , , Example: 3, , 7 180 o, Arc, 4 7, , , ,  210 o ., radian , Radius, 12, 6, 6, , ,  2 , The degree measure corresponding to the given radian  ,  15 , , (a) 21o, Solution: (d), , (d) 60 o, , (c) 100 o, , (b) 210 o, ,  180 , 1c  ,  ;,   , , c, , o, ,  2 ,  2 180 , o, ,    ,   24 ., 15, 15, ,  , , , , The angles of a quadrilateral are in A.P. and the greatest angle is 120o, the angles in radians are

Page 5 :
Trigonometrical Ratios, Functions and Identities 5, (a), Solution: (a), ,  4 5 2, 3, , ,, , 9, , ,, , 9, , ,, , (b), , 3, ,   2 3, 3, , ,, , 2, , ,, , 3, , ,, , (c), , 3, , 5 8 11 12, (d) None of these, ,, ,, ,, 18 18 18, 18, , Let the angles in degrees be   3 ,    ,    ,   3, Sum of the angles  4  360 o, , , , Also greatest angle    3  120 o ,, , Hence, 3  120 o    120 o  90 o  30 o    10 o, ,   90 o, , Hence the angles are 90 o  30 o ,90 o  10 o ,90 o  10 o and 90 o  30 o, That is, the angles in degrees are 60 o , 80 o , 100 o and 120 o,  In terms of radians the angles are 60 , , , 180, , , 80 , , , 180, , , 100 , , , 180, , and 120 , , , , that is, , 180, ,  4  5, 3, , ,, , 9, , ,, , 9, , and, , 2, ., 3, , Example: 4, , The minute hand of a clock is 10 cm long. How far does the tip of the hand move in 20 minutes, (a), , Solution: (b), , 10 , 3, , (b), , 20 , 3, , (c), , 40 , 3, , (d), , We know that the tip of the minute hand makes one complete round in one hour i.e. 60 minutes since, the length of the hand is 10 cm. the distance moved by its tip in 60 minutes  2  10 cm  20 cm, Hence the distance in 20 minutes , , Example: 5, , 30 , 3, , 20 , 20 ,  20 cm , cm ., 60, 3, , The angle subtended at the centre of radius 3 metres by the arc of length 1 metre is equal to, [UPSEAT 1973], , (a) 20o, Solution: (c), , Required angle =, , (b) 60o, , (c) 1/3 radian, , (d) 3 radian, , Arc, 1,  radian ., radius, 3, , 1.5 Trigonometrical Ratios or Functions., In the right angled triangle OMP, we have base = OM = x, perpendicular =PM = y and, hypotenues = OP =r. We define the following trigonometric ratio which are also known as, trigonometric function., Perpendicu lar y, Base, x, cos  , sin  , , , Y, Hypotenues, Hypotenues, r, r, A, , tan  , , Perpendicu lar y, , Base, x, , cot  , , sec  , , Hypotenues, r, , Base, x, , cosec  , , Base, x,  ,, Perpendicu lar y, , P(x,, y), r, , Hypotenues, r, , Perpendicu lar y, , (1) Relation between trigonometric ratio (function), (i) sin  .cosec  1, (ii) tan  . cot   1, cos , sin , (iii) cos  . sec  1, (iv) tan  , (v) cot  , sin , cos , (2) Fundamental trigonometric identities, (i) sin 2   cos 2   1, , (ii) 1  tan 2   sec 2 , Important Tips, , y, , , O, , x, , (iii) 1  cot 2   cosec 2, , M, , X

Page 6 :
6 Trigonometrical Ratios, Functions and Identities, , , If x  sec  + tan  , then, , 1,  sec   tan  ., x, , , , If x  coesc   cot  , then, , 1,  cosec   cot  ., x, , (3) Sign of trigonometrical ratios or functions : Their signs depends on the quadrant in which, the terminal side of the angle lies., r, y, x, y, (i) In first quadrant : x  0, y  0  sin    0, cos    0, tan    0, cosec    0 ,, y, r, r, x, x, r, sec    0 and cot    0 . Thus, in the first quadrant all trigonometric functions are, y, x, positive., (ii), In second quadrant :, y, x, y, r, x, r, x  0, y  0  sin    0, cos    0, tan    0, cosec    0, sec    0 and cot    0 ., r, r, y, x, y, x, Thus, in the second quadrant sin and cosec function are positive and all others are negative., (iii), , sec  , , In third quadrant : x  0, y  0  sin  , , y, x, y, r,  0, cos    0, tan    0, cosec    0 ,, r, r, x, y, , x, r,  0 and cot    0 . Thus, in the third quadrant all trigonometric functions are, y, x, , negative except tangent and cotangent., (iv), , In fourth quadrant :, , x  0, y  0  sin  , , y,  0,, r, , r, r, y, x, cos   0, tan    0, cosec    0 , sec    0 and, y, x, x, r, x, cot    0 Thus, in the fourth quadrant all trigonometric, y, , Y, II, quadrant, S, , X’, , functions are negative except cos and sec., In brief : A crude aid to memorise the signs of, , x < 0, y > 0, sin and cosec, are positive, O, III, quadrant, T, x < 0, y < 0, tan and cot, are positive, , Y’, , trigonometrical ratio in different quadrant. "Add Sugar To, Coffee"., , I, quadrant, A, x > 0, y > 0, All are positive, IV, quadrant, C, x > 0, y < 0, cos and sec, are, positive, , X, , Important Tips, , , First determine the sign of the trigonometric function., , , , If  is measured from X OX i.e., {(  , 2 – )} then retain the original name of the function., , , , 3, , ,    , then change sine to cosine,, If  is measured from Y OY i.e.,    ,, 2, 2, , , Y, , cosine to sine, tangent to cotangent, cot to tan, sec to cosec and cosec to sec., , (4) Variations in values of trigonometric functions in different, quadrants : Let X ' OX and YOY ' be the coordinate axes. Draw a, circle with centre at origin O and radius unity., , B, (0,1) M (x, y), , X, (–1, 0) A, , , O, , x, , Xy, N, , B(0, –, 1), Y, , A (1,, 0), , X

Page 7 :
Trigonometrical Ratios, Functions and Identities 7, , Let M (x , y ) be a point on the circle such that AOM  , , then x  cos , , and y  sin  ;, ,  1  cos  1 and  1  sin   1 for all values of  ., II-Quadrant (S), , I-Quadrant (A), , sin   decreases from 1 to 0, , sin   increases from 0 to, 1, , cos   decreases from 0 to –, 1, , cos   decreases from 1 to, 0, , tan   increases from –  to, 0, , tan   increases from 0 to, , , cot   decreases from 0 to –, , , cot   decreases from  to, 0, , sec   increases from –  to – 1, , sec   increases from 1 to, , , cosec  increases from 1 to , , cosec  decreases from  to 1, , III-Quadrant (T), , IV-Quadrant (C), , sin   decreases from 0 to –, 1, , sin   increases from – 1, to 0, , cos   increases from – 1 to, 0, , cos   increases from 0 to, 1, , tan   increases from 0 to , , tan   increases from – , to 0, , cot   decreases from  to 0, , cot   decreases from 0 to – , , sec   decreases from – 1 to, –, , sec   decreases from  to 1, , cosec  increases from –  to, –1, , Note : , , cosec  decreases from – 1 to, –, ,   and –  are two symbols. These are not real number. When we say that tan , , increases from 0 to  for as  varies from 0 to, , , 2, , it means that tan  increases in the interval, , ,  , . Similarly for other trigonometric,  0,  and it attains large positive values as  tends to, 2,  2, functions., Example: 6, , If sin   cosec   2 , then sin2   cosec 2 , (a) 1, , (b) 4, , [UPSEAT 2002; MP PET 1992; MNR 1990], , (c) 2, , Solution: (c), , (sin   cosec  )  (sin   cosec  )  2 sin  .cosec   2  2  2 ., , Example: 7, , If sin   cos   m and sec   cosec   n , then n(m  1)(m  1) equal to, , 2, , (a) m, Solution: (c), , 2, , 2, , (b) n, , n(m  1)  (sec   cosec  ).2 sin  . cos , 2, , (d) None of these, , 2, , (c) 2m, [m  1  2 sin  . cos  ], 2, , [MP PET 1986], , (d) 2n

Page 8 :
8 Trigonometrical Ratios, Functions and Identities, sin   cos , .2 sin  . cos   2m ., sin  . cos , , , , Example: 8, , If tan  , , (a), Solution: (b), , x sin , y sin , and tan  , , then x / y equal to, 1  x cos , 1  y cos , , sin , sin , , (b), , (c), , sin , 1  cos , , (d), , sin , 1  cos , , x sin   tan   x cos  . tan , , x, , tan , sin , , sin   cos  tan  sin  cos   cos  sin , y, , Similarly,, , Example: 9, , sin , sin , , [MP PET 1991], , sin , ;, sin  cos   cos  sin , , The equation sec 2  , , , , x, sin , , ., y, sin , , 4 xy, is only possible when [MP PET 1986; IIT 1996; Karnataka CET 1997; AMU, (x  y)2, , 1987, 1991], , Solution: (a), , (c) x  y, , (a) x  y, , (b) x  y, ,  cos 2   1  sec 2  , , 4 xy,  1  4 xy  (x  y )2  (x  y)2  0, (x  y)2, , Which is possible only when x  y, Example: 10, , Example: 11, , (c) sec   tan , , (b) 1, , (1  sin  ) 2, (1  sin 2  ), , , , If tan A  cot A  4 , then tan 4 A  cot 4 A is equal to, (b) 191, , If sin x  cos x , (a), , Solution: (d), , 25, 17, , (d) 194, , 24, 25, ,  tan 4 A  cot 4 A  194 ., , 7, 25, , [UPSEAT 2003], , (c), , 25, 7, , (d), , 24, 7, , 1, 1,  sin 2 x  cos 2 x  2 sin x cos x , 25, 5, , 7, 24, 24,  cos 2 x  ,  tan 2 x , ., 25, 7, 25, , If sin x  , (a), , 24, , then the value of tan x is, 25, , (b), , 24, 7, 2, , Solution: (b), , (c) 80, , 1, , then tan 2 x is, 5, , (b), , sin x  cos x , sin 2 x  , , Example: 13, , [Kerala (Engg.) 2002], , tan A  cot A  4  tan 2 A  cot 2 A  2 tan A cot A  16,  tan 2 A  cot 2 A  14  tan 4 A  cot 4 A  2  196, , Example: 12, , (d) sec  . tan , , 1  sin ,  sec   tan  ., cos , , (a) 110, Solution: (d), , ( x , y  R), , 1  sin , equals, 1  sin , , (a) 0, Solution: (c), , (d) None of these, , [UPSEAT 2003], , (c), , 25, 24, , 7, sin x 24,   24 , cos x  1  sin 2 x  1  , ,  tan x , .,  , 25, 25, cos, x, 7, , , , (d) None of these

Page 9 :
Trigonometrical Ratios, Functions and Identities 9, Example: 14, , If tan   sec   e x , then cos  equals, (a), , Solution: (b), , (e x  e  x ), 2, , (b), , 2, (e  e  x ), , For 0   , , , 2, , , , , if x , , , , , , , , cos 2n , y , , n 0, , , , 2, ., e x  e x, , sin 2n , z , , n 0, , (b) xyz  xy  z, ,  cos, ,  sin 2n  ,then, , 2n, , n 0, , (c) xyz  x  y  z, , 1, 1, 1, 1, 1, 1, xy, , , , y, , z, , , xy  1, 1  cos 2  sin 2 , 1  sin 2  cos 2 , 1  cos 2  sin 2  1  1, xy, ,  xyz  z  xy  xyz = xy + z, , ......(i), , Also,, , 1 1,   cos 2   sin 2   1  x  y  xy ; From (i), xyz = x + y + z., x y, , If P , , cos , 2 sin , and Q , , then, 1  sin   cos , 1  sin , , (a) PQ  1, Solution: (d), , PQ, , (d) Both (b) and (c), , a, 1r, , We get, x =, , Example: 16, , (e x  e  x ), (e x  e  x ), , ........(ii), , (a) xyz  xz  y, From s , , (d), , ........(i), x, , From (i) and (ii),  2 sec   e x  e  x  cos  , , Solution: (d), , (e x  e  x ), 2, , (c), , x, , tan   sec   e x,  sec   tan   e, , Example: 15, , [AMU 2002], , (b), , Q, 1, P, , [MP PET 2001], , (c) Q  P  1, , (d) Q  P  1, , 2 sin , cos , , 1  sin   cos  1  sin , , After solving, P  Q  1 ., Example: 17, , The value of 6(sin 6   cos 6  )  9(sin 4   cos 4  )  4 equals to, (a) – 3, , Solution: (c), , (b) 0, , (c) 1, , [MP PET 2001, 1997], , (d) 3, , = 6(sin6   cos 6  )  9(sin4   cos 4  )  4, = 6[(sin2   cos 2  )3  3 sin 2  cos 2  (sin 2   cos 2  )]  9[(sin2   cos 2  )2  2 sin 2  . cos 2  ]  4, = 6[1  3 sin 2  cos 2  ]  9[1  2 sin 2  cos 2  ]  4 = 6  9  4  1 ., , Example: 18, , sin , cos , , equals to, 1  cot  1  tan , , (a) 0, Solution: (d), , (b) 1, , [Karnataka CET 1998], , (c) cos   sin , , (d) cos   sin , , cos 2   sin 2 , sin 2 , cos 2 , sin  . sin , cos  . cos , ,  cos   sin  ., =, =, , (sin   cos  ) (cos   sin  ), (cos   sin  ), sin  (1  cot  ) (1  tan  ) cos , , 1.6 Trigonometrical Ratios of Allied Angles., Two angles are said to be allied when their sum or difference is either zero or a multiple of, 90 ., o

Page 10 :
10 Trigonometrical Ratios, Functions and, Identities, , (1) Trigonometric ratios of (–): Let a revolving ray starting from, its initial position OX , trace out an angle XOA   . Let P(x, y) be, a point on OA such that OP = r. Draw PM  from P on x-axis. Angle, XOA '   in the clockwise sense. Let P' be a point on OA ' such, that OP '  OP . Clearly M and M  coincide and OMP is congruent, to OMP ' then P' are (x, – y)., y, y, x, y, sin(  ) , ,   tan ,   sin  ; cos( )   cos  ; tan(  ) , r, x, r, r, Taking the reciprocal of these trigonometric ratios;, cosec (  )   cosec  ,, sec(  )  sec , and cot(  )   cot , , Note :, , Y, A, P(x,, y), , r, , , , X, , – M, , O, , r, , P (x, –, y), A, ,  A function f (x ) is said to be an even function if f ( x )  f (x ) for all x in its domain.,  A function f (x ) is said to be an odd function if f ( x )   f (x ) for all x in its domain.,  sin  , tan  , cot  , cosec are odd functions and cos  , sec  are even functions., , (2) Trigonometric function of (90 –  ) : Let the revolving line, starting, from OA, trace out any acute angle AOP, equal to . From any point P,, draw PM  to OA. Three angles of a triangle are together equal to two, right angles, and since OMP is a right angle, the sum of the two angles, , P, 90o–, , , , 90, , o, A, MOP and OPM is right angle. OPM  90 o  , O, M, [When the angle OPM is consider, the line PM is the ‘base’ and MO is, the ‘perpendicular’], MO, PM, cos(90 o   )  cos MPO , sin( 90 o   )  sin MPO ,  cos AOP  cos  ,,  sin AOP  sin , PO, PO, MO, PM, tan( 90 o   )  tan MPO ,  cot AOP  cot  ,, cot(90 o   )  cot MPO ,  tan AOP  tan , PM, MO, PO, PO, cosec(90 o   )  cosec MPO ,  sec AOP  sec  , sec(90 o   )  sec MPO ,  cosec AOP  cosec, MO, PM, (3) Trigonometric function of (90+ ) : Let a revolving ray OA starting from its initial poisiton, OX, trace out an angle XOA   and let another revolving, Y, ray O A starting from the same initial position OX, first, A, A, trace out an angle . So as to coincide with OA and then it, , revolves through an angle of, , 90 o, , in anticlockwise, , direction to form an angle XOA '  90 o   ., X, Let P and P' be points on OA and OA ' respectively, such that OP  OP '  r ., Draw perpendicular PM and PM ' from P and P', respectively on OX . Let the coordinates of P be (x, y)., Then OM  x and PM  y clearly, OM '  PM  y and P ' M '  OM  x ., , (–y,, x), , , , , , M, , O, , , , P(x,, y), M, , X, , Y, , So the coordinates of P ' are –y, x, M ' P' x, OM '  y, sin( 90   ) ,   cos  ,, cos(90   ) , ,   sin , OP ', r, OP ', r, M ' P', x, x, tan( 90   ) , , ,   cot  , cot(90   )   tan  , sec(90   )  cosec , cosec(90   )  sec, OM '  y, y

Page 11 :
Trigonometrical Ratios, Functions and Identities 11, (90 – ), , (θ), , Allied, angles, , or, , Trigo. Ratio, , (180  θ), or, , ( 90  θ), or, , π, ,  θ, 2, , , (π  θ), , π, ,  θ, 2, , , , (180  θ) (270  θ), or, or, ( π  θ),  3π, , , (270  θ), or, , θ, ,  2, , ,  3π, , θ, ,  2, , , ( 360  θ), or, (2 π  θ), , – sin, , cos, , cos , , sin, , – sin, , – cos, , – cos , , – sin, , cos, , cos, , sin, , – sin, , – cos, , – cos, , – sin, , sin, , cos, , tan , , – tan, , cot, , – cot, , – tan, , tan, , cot, , – cot, , – tan, , sin, , Important Tips, , , sin n   0, cos n   (1), , , , sin(n    )  (1)n sin  , cos( n    )  (1)n cos , , , ,  n, , sin,     (1), 2, , , , n, , n 1, 2, , cos  , if n is odd, , = (1)n / 2 sin  , if n is even, , ,  n, , cos ,     (1),  2, , , n 1, 2, , sin  , if n is odd, ,  (–1)n / 2 cos  , if n is even, , 1.7 Trigonometrical Ratios for Various Angles., 0, 0, , /6, , sin, , , , 1/2, , /4, 1/ 2, , cos, , 1, , 3 /2, , tan, , 0, , 1/ 3, , 1/ 2, 1, , /3, , /2, , , , 3 /2, 1/2, , 1, , 0, , 3/2, –1, , 2, 0, , 0, , –1, , 0, , 1, , 3, , , , 0, , , , 0, , 1.8 Trigonometrical Ratios in terms of Each other, sin, sin, , cos, tan, , cos, , sin, , 1  cos 2 , , 1  sin 2 , , cos, , sin , , 1  cos 2 , cos , cos , , 1  sin , 2, , cot , , sec, , 1  sin 2 , sin , 1, 1  sin , 1, sin , 2, , cosec, , 1  cos , 2, , tan, tan , , cot, 1, , 1  tan , , 1  cot , , 1, , cot , , 2, , 1  tan , 2, , tan, 1, tan , , 1, cos , , 1  tan 2 , , 1, , 1  tan 2 , tan , , 1  cos , 2, , sec, 2, , 1  cot , 1, cot , 2, , cot, 1  cot 2 , cot , 1  cot 2 , , sec 2   1, sec , 1, sec , sec 2   1, , 1, , cosec, 1, co sec, cosec 2  1, cosec, 1, cosec 2  1, cosec 2  1, , sec   1, 2, , sec, sec , sec   1, 2, , cosec, cosec 2  1, , cosec

Page 12 :
12 Trigonometrical Ratios, Functions and, Identities, , Important Tips, , , Values for some standard angles, 3 1, , sin 15 o  cos 75 o , , ;, , cos 15 o  sin 75 o , , 5 1, ;, 4, , cos 36 o  sin 54 o , , 2 2, sin 18 o  cos 72 o , , 2 2, ,, 2, , sin 22, , 1o, 1o,  cos 67, , 2, 2, , tan 22, , 1o, 1o,  cot 67,  2 1, 2, 2, , Example: 19, , cos 22, , tan 15 o  cot 75 o  2  3 ;, , ;, , 5 1, ;, 4, , 1o, 1o,  sin 67, , 2, 2, , tan 75 o  cot 15 o  2  3, , 1o, 1o, 2 2,  tan 67, , ; cot 22, 2, 2, 2, , [MNR 1979], , 2 3, 2, , 3 1, , (b), , 2 2, , (a), , 1, , , , 3 1, 2 2, , 3 1, 1, 3 1,  , , ., 2, 2, 2, 2 2, , 5, is, 4, , 1, , (b), , 2, , (d), , 2 2, , sin 75 o  sin(45 o  30 o )  sin 45 o cos 30 o  sin 30 o cos 45 o , , The value of cos A  sin A , when A , , 3 1, , (c) , , 2, , Example: 20, , 2 1, , sin 75 o =, (a), , Solution: (b), , 3 1, 2 2, , [MP PET 1990], , (c) 0, , 2, , (d) 1, , 5, 5, , , 1, 1,  sin,   cos  sin  , , 0., 4, 4, 4, 4, 2, 2, , Solution: (c), , cos, , Example: 21, , tan A  cot(180 o  A)  cot(90 o  A)  cot(360 o  A) equal to, , (a) 0, , (b) 2 tan A, , Solution: (a), , tan A  cot A  ( tan A)  ( cot A)  0 ., , Example: 22, , The value of cos 15 o  sin 15 o equal to, , [MP PET 1992], , (c) 2 cot A, , (d) 2(tan A  cot A), , [UPSEAT 1975; MP PET 1994; MP PET, , 2002], , 1, , (a), , Example: 23, , 2, , 3 1, , Solution: (a), , 2 2, , , , 3 1, 2 2, , =, , 1, 2, , (c), , 1, 2, , (d) Zero, , ., , , , , ,  3, , , , 3 sin 4 ,     sin 4 3     2 sin6      sin6 5   ,  2, , 2, , , , , , , (a) 0, Solution: (b), , 1, 2, , (b), , (b) 1, , [IIT 1986], , (c) 3, , (d) sin 4  sin 6, , =, , 3[( cos  )  ( sin  ) ]  2[ cos   sin  ], , =, , 3[(cos 2   sin 2  )2  2 sin 2  cos 2  ]  2[(cos 2   sin 2  )3  3 cos 2  sin 2  (cos 2   sin 2  )], , =, , 3  6 sin 2  cos 2   2  6 sin 2  cos 2  = 1., , 4, , 4, , 6, , 6

Page 13 :
Trigonometrical Ratios, Functions and Identities 13, Trick : Put   0,, Example: 24, , , 2, , ; then the value of expression remains constant i.e., it is independent of ., , Which of the following number is rational, (a) sin 15 o, , Solution: (c), , [IIT 1998], , (c) sin 15 o . cos 15 o, , (b) cos 15 o, , sin 15 o = sin(45 o  30 o ) =, , 3 1, , = irrational  cos 15 o  cos( 45 o  30 o ) , , 2 2, sin 15 o . cos 15 o , , 3 1, 2 2, , (d) sin 15 o . cos 75 o, = irrational, , 1, 1, 1, (2 sin 15 o cos 15 o )  sin 30 o  = rational, 2, 2, 4, 2, ,  3 1,   4  2 3  irrational., sin 15 o . cos 75 o  sin 15 o . sin 15 o  sin 2 15 o = ,  2 2 , 8, , , , Example: 25, , If sin x  sin 2 x  1 , then the value of cos 12 x  3 cos 10 x  3 cos 8 x  cos 6 x  2 is, (a) 0, , Solution: (c), , (c)  1, , (b) 1, , [MP PET 2001], , (d) 2, , Since sin x  sin 2 x  1  sin x  1  sin 2 x  cos 2 x, , ........(i), , From given expression, cos 6 x (cos 6 x  3 cos 4 x  3 cos 2 x  1) – 2 = cos 6 x (cos 2 x  1)3  2, From (i) sin x  cos 2 x,  sin 3 x (sin x  1)3  2 = (sin 2 x  sin x )3  2  1  2  1 ., Example: 26, , If 4 sin   3 cos  then, , (a), Solution: (b), , 25, 16, , sec 2 , 4[1  tan 2  ], , (b), , Given 4 sin   3 cos   tan  , , equals to, , 25, 28, , (c), , 1, 4, , (d) 1, , 3, 4, , 9, 1, sec 2 , 1  tan 2 , 25, 16, , The given expression is, =, ., , 2, 2, 9, 4 [1  tan  ] 4 (1  tan  ), ,  28, 4 1 , , 16 , , , 1.9 Formulae for the Trigonometric Ratios of Sum and Differences of Two Angles., (1) sin( A  B)  sin A cos B  cos A sin B, , (2) sin( A  B)  sin A cos B  cos A sin B, , (3) cos( A  B)  cos A cos B  sin A sin B, , (4) cos( A  B)  cos A cos B  sin A sin B, , (5) tan( A  B) , , tan A  tan B, 1  tan A tan B, , (6) tan( A  B) , , tan A  tan B, 1  tan A tan B, , (7) cot( A  B) , , cot A cot B  1, cot A  cot B, , (8) cot( A  B) , , cot A cot B  1, cot B  cot A, , (9) sin( A  B). sin( A  B)  sin 2 A  sin 2 B  cos 2 B  cos 2 A, (10) cos( A  B). cos( A  B)  cos 2 A  sin 2 B  cos 2 B  sin 2 A, (11) tan A  tan B , , sin A sin B sin A cos B  cos A sin B, sin( A  B), , , , cos A cos B, cos A cos B, cos A. cos B, , , , ,  A  n  , B  m  , 2, , 

Page 14 :
14 Trigonometrical Ratios, Functions and, Identities, , , ,  A  n , B  m   , 2, , , sin( B  A), sin A. sin B, , (12) cot A  cot B , , 1.10 Formulae for the Trigonometric Ratios of Sum and Differences of Three Angles., (1) sin( A  B  C)  sin A cos B cos C  cos A sin B cos C  cos A cos B sin C  sin A sin B sin C, or sin ( A  B  C)  cos A cos B cos C(tan A  tan B  tan C  tan A. tan B. tan C), (2) cos( A  B  C)  cos A cos B cos C  sin A sin B cos C  sin A cos B sin C  cos A sin B sin C, , cos( A  B  C)  cos A cos B cos C(1  tan A tan B  tan B tan C  tan C tan A), (3) tan( A  B  C) , (4) cot( A  B  C) , , tan A  tan B  tan C  tan A tan B tan C, 1  tan A tan B  tan B tan C  tan C tan A, , cot A cot B cot C  cot A  cot B  cot C, cot A cot B  cot B cot C  cot C. cot A  1, , In general;, (5) sin( A1  A 2  ......  A n ) = cos A1 cos A 2 ..... cos A n (S 1  S 3  S 5  S 7  ...), (6) cos( A1  A 2  ....  A n )  cos A1 cos A 2 ... cos A n (1  S 2  S 4  S 6 ....), (7) tan( A1  A 2  .....  A n ) , , S 1  S 3  S 5  S 7  ...., 1  S 2  S 4  S 6  ...., , S 1  tan A1  tan A 2  ....  tan A n = The sum of the tangents of the separate, , Where;, angles., , S 2  tan A1 tan A 2  tan A1 tan A 3  .... = The sum of the tangents taken two at a time., , S 3  tan A1 tan A2 tan A3  tan A2 tan A3 tan A4  ... = Sum of tangents three at a time, and, , so on., If A1  A 2  ....  A n  A, then, , S 1  n tan A , S 2  n C 2 tan 2 A , S 3  n C 3 tan 3 A,...., , (8) sin nA  cos n A(n C1 tan A  n C 3 tan 3 A  n C 5 tan 5 A  ....), (9) cos nA  cos n A(1  n C 2 tan 2 A  n C 4 tan 4 A  ...), (10) tan nA , , C1 tan A  n C 3 tan 3 A  n C 5 tan 5 A  ...., 1  n C 2 tan 2 A  n C 4 tan 4 A  n C 6 tan 6 A  ..., n, , (11) sin nA  cos nA  cos n A(1 nC1 tan A nC2 tan 2 A nC3 tan 3 A nC4 tan 4 A nC5 tan 5 A nC6 tan 6 A  .....), (12) sin nA  cos nA  cos n A(1  n C1 tan A  n C 2 tan 2 A  n C 3 tan 3 A  n C 4 tan 4 A  n C 5 tan 5 A  n C 6 tan 6 A...), (13) sin( )  sin(   )  sin(  2  )  .....  sin(  (n  1) ) =, , sin{  (n  1) ( / 2)}. sin( n / 2), sin(  / 2)

Page 15 :
Trigonometrical Ratios, Functions and Identities 15, , ,    ,   , cos   (n  1) . sin n ,  2 , ,   2 , (14) cos( )  cos(   )  cos(  2  )  ....  cos(  (n  1) ) =, , sin  , 2, , 1.11 Formulae to Transform the Product into Sum or Difference., (1) 2 sin A cos B  sin( A  B)  sin( A  B), , (2) 2 cos A sin B  sin( A  B)  sin( A  B), , (3) 2 cos A cos B  cos( A  B)  cos( A  B), , (4) 2 sin A sin B  cos( A  B)  cos( A  B), , Let A  B  C and A  B  D, Then, A , , CD, CD, and B , 2, 2, , Therefore, we find out the formulae to transform the sum or difference into product., (5) sin C  sin D  2 sin, , CD, CD, cos, 2, 2, , (7) cos C  cos D  2 cos, , (6) sin C  sin D  2 cos, , CD, CD, cos, 2, 2, , (8) cos C  cos D  2 sin, , CD, CD, sin, 2, 2, , CD, DC, CD, CD, sin,  2 sin, sin, 2, 2, 2, 2, , Important Tips, 1, , , , sin(60 o   ). sin  sin(60 o   ) , , , , o, o, tan( 60  ). tan  tan( 60  ) tan 3, , , , sin 2 n A, cos A. cos 2 A. cos 2 2 A. cos 2 3 A....... cos 2 n1 A  n, , if A  n, 2 sin A, , 4, ,  cos(60   ). cos  cos(60 o   ) , , sin 3, , 1, 4, , cos 3, , = 1, if A  2n, = 1, if A  (2n  1), , Example: 27, , cos 12 o  sin 12 o, cos 12  sin 12, o, , (a) 2 tan 33 o, 1  tan 12 o, , o, , , , sin 147 o, cos 147 o, , , , [MP PET 1991], , (b) 1, , =, , Example: 28, , If sin  1  sin  2  sin  3  3 , then cos  1  cos  2  cos  3 , (a) 3, , Solution: (d), , (b) 2, , (c) 1, , (d) 0, , We know | sin  |  1 ; So, each 1 ,  2 and  3 must be equal to  / 2, , , Example: 29, , (d) 0, ,  tan 147 o = tan( 45 o  12)  tan(180 o  33 o )  tan 33 o  ( tan 33 o )  0 ., , Solution: (d), , 1  tan 12 o, , (c) – 1, , cos  1  cos  2  cos  3  0 ., , cos A  cos(240 o  A)  cos(240 o  A) , , [MP PET 1991]

Page 16 :
16 Trigonometrical Ratios, Functions and, Identities, (a) cos A, Solution: (b), , (b) 0, , (c), , (d), , 3 sin A, , 3 cos A, , cos A  [2 cos 240 o cos A] = cos A  2( cos 60 o ) cos A, ,  1 , = cos A 1  2   0 .,  2 , , , Example: 30, , sin 2 A  sin 2 B, , sin A cos A  sin B cos B, , [MP PET 1993], , Solution: (b), Example: 31, , Solution: (c), , (c) cot( A  B), , (b) tan( A  B), , (a) tan( A  B), , (d) cot( A  B), , 2(sin 2 A  sin 2 B), 2 sin( A  B). sin( A  B), 2 sin( A  B) sin( A  B),  tan( A  B) ., =, , sin 2 A  sin 2 B, 2 sin A cos A  2 sin B cos B, 2 sin( A  B) cos( A  B), , The expression cos 2 ( A  B)  cos 2 B  2 cos( A  B) cos A cos B is, (a) Dependent on B, , (b) Dependent on A and B, , (c) Dependent on A, , (d) Independent of A and B, , cos 2 ( A  B)  cos 2 B  cos( A  B)[cos( A  B)  cos( A  B)], , , , cos 2 B  cos( A  B) cos( A  B)  cos 2 B  (cos 2 A  sin 2 B)  1  cos 2 A, , Trick : Put A  90 o and 0o the value is sin 2 B  cos 2 B  1 and 0 again put B  0 o , 90o and the value is, sin 2 A and sin 2 A means expression depends on A., , Example: 32, , If tan  , (a), , Solution: (b), , m, 1, and tan  , then    , 2m  1, m 1, , , 3, , (b), , We have tan  , , , 4, , [IIT 1978], , (c), , 2m 2  2m  1, 2m  2m  1, , Hence    , , 2, , (d) None of these, , m, 1, and tan  , 2m  1, m 1, , m, 1, , 2m 2  m  m  1, m, , 1, 2, m, 1 , tan(   ) , m, 1, 2m 2  m  2m  1  m, 1, ., (m  1) (2m  1), , , , 6, ,  1  tan(   )  tan, , , tan   tan  ,  tan(   ) , , 1,  tan  tan  , , , , 4, , , 4, , Trick : As    is independent of m, therefore put m  1, then tan  , 1 1, , , Therefore, tan(   )  2 3  1 , Hence    , 1, 4, 1, 6, , Example: 33, , Solution: (d), , 1, 1, and tan   ., 2, 3, , (Also check for other values of m), , If tan   cot   a and sin   cos   b , then (b 2  1) 2 (a 2  4 ) , (a) 2, , (b)  4, , Given that tan   cot   a, , …….(i), , [WB JEE 1979], , (c)  4, and, , sin   cos   b, , …….(ii), , (d) 4

Page 17 :
Trigonometrical Ratios, Functions and Identities 17, Now, (b 2  1) 2 (a 2  4 )  {(sin   cos  ) 2  1} 2 {tan   cot  ) 2  4}, 1 ,  1,  [1  sin 2  1]2 [tan 2   cot 2   2  4 ]  sin 2 2 (cosec 2  sec 2  )  4 sin 2  cos 2   2 , 4, 2 ,  sin  cos  , , Trick : Obviously the value of expression (b 2  1) 2 (a 2  4 ) is independent of  , therefore put any, suitable value of . Let   45 o , we get a  0 , b  2 so that [( 2 )2  1]2 (0 2  4 )  4 ., Example: 34, , If sin B =, (a), , Solution: (c), , tan( A  B), 1, sin(2 A  B) , then, , 5, tan A, , 5, 3, , (b), , 2, 3, , (c), , 3, 2, , (d), , 3, 5, , sin(2 A  B) 5, sin(2 A  B)  sin B 5  1, , by componendo and Dividendo., , sin B, 1, sin(2 A  B)  sin B 5  1, , tan( A  B) 3, 2 sin( A  B). cos A 6,  ., , , tan A, 2, 2 cos( A  B). sin A 4, , Example: 35, , sin 70 o  cos 40 o, , cos 70 o  sin 40 o, , [Karnataka CET 1986; MP PET, , 1999], , (a) 1, , 1, , (b), , 3, , (c), , (d), , 3, , Solution: (c), , sin 70 o  cos 40 o, sin 60 o, 3 2, sin 70 o  sin 50 o, 2 sin 60 o cos 10 o, , .  3 ., =, =, , o, o, o, o, o, o, 2 1, sin 30 o, cos 70  sin 40, sin 20  sin 40, 2 sin 30 cos(10 ), , Example: 36, , sin 47 o  sin 61o  sin 11o  sin 25 o , , 1, 2, , [EAMCET, , 2003;, , MP, , PET, , 2001], , (a) sin 36 o, Solution: (d), , (b) sin 7 o, , (c) cos 36 o, , sin 47 o  sin 61o  (sin 11o  sin 25 o ) = 2 sin 54 o. cos 7 o  2 sin 18 o cos 7 o, , = 2 cos 7 o (sin 54 o  sin 18 o ) = 2 cos 7o.2 cos 36 o. sin 18 o = 4 . cos 7 o., Example: 37, , (d) cos 7 o, , 5 1 5 1, .,  cos 7 o ., 4, 4, , cos 10 o  sin 10 o, , cos 10 o  sin 10 o, , (a) tan 55 o, , (b) cot 55 o, , (c)  tan 35 o, , Solution: (b), , cos 10 o  sin 10 o 1  tan 10 o, ,  tan 35 o  tan( 90 o  35 o ) = cot 55 o ., cos 10 o  sin 10 o 1  tan 10 o, , Example: 38, , If tan( A  B)  p and tan( A  B)  q then the value of tan 2 A , (a), , pq, pq, , (b), , pq, 1  pq, , Solution: (d), , 2 A  {( A  B)  ( A  B)}  tan 2 A , , Example: 39, , sin 163 o cos 347 o  sin 73 o sin 167 o , (a) 0, , (b), , (c), , 1  pq, 1 p, , (d)  cot 35 o, , (d), , pq, 1  pq, , tan( A  B)  tan( A  B), pq,  tan 2 A , 1  tan( A  B). tan( A  B), 1  pq, [MP PET 2000], , 1, 2, , (c) 1, , (d) None of these, , Solution: (b), , sin(90 o  73 o ). cos(360 o  13 o )  sin 73 o. sin(180 o  13 o ) = cos 73 o. cos 13 o  sin 73 o. sin 13 o  cos(73 o  13 o )  cos 60 o  1 ., , Example: 40, , The value of cot 70 o  4 cos 70 o is, , 2

Page 18 :
18 Trigonometrical Ratios, Functions and, Identities, , 1, , (a), , Solution: (b), , cot 70 o  4 cos 70 o , , (c) 2 3, , 3, , (d), , 1, 2, , cos 70 o  2 sin 140 o, cos 70 o  4 sin 70 o. cos 70 o, , o, sin 70, sin 70 o, , cos 70 o  2 sin(180  40 o ) sin 20 o  sin 40 o  sin 40 o, , sin 70 o, sin 70 o, , , , sin 80 o  sin 40 o 2 sin 60 o cos 20 o, 2 sin 30 o cos 10 o  sin 40 o, , ,  3., sin 70 o, sin 70 o, sin 70 o, , , , Example: 41, , (b), , 3, , If tan   (1  2  x )1 , tan   (1  2 x 1 )1 , then    equals, (a), , , 6, , (b), , , 4, , [AMU 2002], , (c), , , 3, , (d), , , 2, , 1, , Solution: (b), , 1, , 1, 1, , 2 x 1, 1 x, tan   tan , 2, tan(   ) ,  tan(   ) , 1, 1, 1  tan  tan , 1, ., 1 1  2 x 1, 1 x, 2, tan(   ) , , , Example: 42, , The value of, , 2 x  2 .2 x  x  2 x  1, , ,  tan(   )  1  tan,  ., 4, 4, 1  2 x  2 .2 x  2 .2 x  x  2 x, , tan 70 o  tan 20 o, , tan 50 o, , (a) 1, , Solution: (b), , [Karnataka CET 2003], , (b) 2, , (c) 3, , (d) 0, , sin 70 o, sin 20 o, sin 70 o cos 20 o  cos 70 o sin 20 o, , o, o, 2 sin(70 o  20 o ) cos 50 o, 2 sin 50 o . cos 50 o, cos 70, cos 20 , cos 70 o. cos 20 o, , , =, 2 cos 70 o . cos 20 o . sin 50 o, sin 50 o, sin 50 o, 2 cos 70 o cos 20 o . sin 50 o, o, o, cos 50, cos 50, , =, , 2 cos 50 o, 2 cos 50 o, , 2., cos 90 o  cos 50 o 0  cos 50 o, , 1.12 Trigonometric Ratio of Multiple of an Angle., (1) sin 2 A  2 sin A cos A , , 2 tan A, 1  tan 2 A, , (2) cos 2 A  2 cos 2 A  1  1  2 sin 2 A  cos 2 A  sin 2 A , (3) tan 2 A , , 2 tan A, 1  tan 2 A, , 1  tan 2 A, , ; where A  (2n  1) ., 2, 1  tan A, 4, , (4) sin 3 A  3 sin A  4 sin 3 A  4 sin( 60 o  A). sin A. sin( 60 o  A), , (5) cos 3 A  4 cos 3 A  3 cos A  4 cos(60 o  A). cos A. cos(60 o  A), (6) tan 3 A , , 3 tan A  tan 3 A,  tan( 60 o  A). tan A. tan( 60 o  A) , where A  n   / 6, 1  3 tan 2 A, , (7) sin 4  4 sin  . cos 3   4 cos  sin 3  (8) cos 4  8 cos 4   8 cos 2   1, (9) tan 4 , , 4 tan   4 tan 3 , 1  6 tan 2   tan 4 , , (10) sin 5 A  16 sin 5 A  20 sin 3 A  5 sin A, , (11) cos 5 A  16 cos 5 A  20 cos 3 A  5 cos A

Page 19 :
Trigonometrical Ratios, Functions and Identities 19, , 1.13 Trigonometric Ratio of Sub-multiple of an Angle., (1) sin, , 3, , A, A, A, A, , If 2n    / 4  A / 2  2n  ,  cos,  1  sin A or sin  cos   1  sin A i.e., , 4, 2, 2, 2, 2, ,  , otherwise, , (2) sin, , 5, , A, A, A, A, , If 2n    / 4  A / 2  2n  ,  cos,  1  sin A or (sin  cos )   1  sin A i.e., , 4, 2, 2, 2, 2, ,  , otherwise, A  tan 2 A  1  1, 1  cos A 1  cos A, , , , , where A  (2n  1), 2, tan A, 1  cos A, sin A, , (3) (i) tan, , (ii) cot, , A, 1  cos A 1  cos A, , where A  2n, , , 2, 1  cos A, sin A, , The ambiguities of signs are removed by locating the quadrants in which, , 2, , follow the following figure,, , A, +, 2 cos, A, sin, –, 2, cos, , 3, 4, , sin, , sin, , A, A, is –ve, + cos, 2, 2, , sin, , A, – cos A is, 2, 2, +ve, , , , sin, , 5, 4, , sin, , A, is +ve, 2, , A, lies or you can, 2, , , 4, , A, is+ve, 2, sin, , A, A, + cos is +ve, 2, 2, , sin, , A – cos A is –ve, 2, 2, , A, A, + cos, is –ve, 2, 2, , A, – cos, 2, 3, , 7, 4, , A, is –, 2 ve, , 2, , (4) tan 2, , A 1  cos A, ; where A  (2n  1), , 2 1  cos A, , (5) cot 2, , A 1  cos A, ; where A  2n, , 2 1  cos A, , Important Tips, n   (1)n A, ., 2, , , , Any formula that gives the value of sin, , A, 2, , , , Any formula that gives the value of cos, , A, 2n   A, in terms of cos A shall also give the value of cos of, ., 2, 2, , , , Any formula that gives the value of tan, , A, n  A, in terms of tan A shall also give the value of tan of, ., 2, 2, , Example: 43, , If sin  , , in terms of sin A shall also give the value of sine of, , 3, , 3, where    , , then cos equal to, 5, 2, 2, , [MP PET 1998]

Page 20 :
20 Trigonometrical Ratios, Functions and, Identities, , 1, , (a), , (b) , , 1, , 3, , (c), , 10, , 10, , 3, , (d), , 10, , 10, , Solution: (d), , , 3,   3, , 4,  cos ,   ,   ,  cos  ve   cos  , 2, 2, 2 2, 4, 5, 2, , Example: 44, , 2 sin 2   4 cos(   ) sin  sin   cos 2(   ) equal to, , 1  cos , , 2, , 1, 2, , 4, 5 , , 9, 3, , ., 10, 10, , [UPSEAT, , 1993;, , IIT, , 1977], , (a) sin 2, Solution: (c), , (c) cos 2, , (b) cos 2 , , (d) sin 2 , , Since 2 cos(   )  2 cos (   )  1, 2 sin   1  cos 2    cos 2   2 cos(   )[2 sin  sin   cos(   )], 2, , 2, ,   cos 2   2 cos(   ). cos(   )   cos 2   cos 2  cos 2   cos 2 ., , Example: 45, , cot 2 15 o  1, =, cot 2 15 o  1, , (a), , Solution: (b), , [MP PET 1998], , 1, 2, , (b), , , 1 , 1, 1 , , 1  tan 2 15 1  [tan( 45 o  30 o )]2, , , , 2, o, o 2, 1  tan 15 1  [tan( 45  30 )], , 1 , 1, 1 , , , , Trick : cos 2 , Example: 46, , (c), , 3 3, 4, , (d), , 3, , 2, , 1 , , 3 , , 1 , 1, , 3  =, 2, , 1 , 1, , 3 , , 1 , 3 , , 2, , 3 1, , 3  1 , [ 3  1]2  [ 3  1]2 4 3, 3, , , , 2, 2, 2, 8, 2, [, 3, , 1, ], , [, 3, , 1, ], , 3 1, , 3  1 , , 1  tan 2 , 1  tan 2 15 o, 3, ,  cos 30 o , ., 2, 2, o, 2, 1  tan , 1  tan 15, , If sin 6  32 cos 5  . sin  32 cos 3  sin  3 x , then x =, (b) cos 2, , (a) cos , Solution: (d), , 3, 2, , [EAMCET 2003], , (c) sin , , (d) sin 2, , sin 6  2 sin 3 . cos 3 = 2[3 sin   4 sin 3  ][4 cos 3   3 cos  ], , = 24 sin  . cos  (sin 2   cos 2  )  18 sin  cos   32 sin 3  cos 3  = 32 cos 5  . sin  32 cos 3  . sin  3 sin 2, On comparing, x  sin 2, Trick : Put   0 o , then x  0 . So, option (c) and (d) are correct., Now put   30 o , then x , Example: 47, , If, , x, , 1, , 3, . Therefore, Only option (d) is correct., 2, ,  2 cos  , then x 6  x 6 , , [Karnataka CET 2003], , x, , (a) 2 cos 6, Solution: (b), , Given,, , x, , (b) 2 cos 12, 1, , (c) 2 cos 3, ,  2 cos , , (d) 2 sin 3, ........(i), , x, , On squaring both sides we get, x , x, , 1,  2(2 cos 2   1)  2 cos 2, x, , Again squaring both sides,, , 1, 1,  2  4 cos 2   x   4 cos 2   2, x, x, , ........(ii)

Page 21 :
Trigonometrical Ratios, Functions and Identities 21, x2 , , 1, 1, 1,  2  4 cos 2 2  x 2  2  4 cos 2 2  2  2(2 cos 2 2  1)  x 2  2  2 cos 4, 2, x, x, x, , ......(iii), , 3, , 1 , 1, 1 , 1 , , Now taking cube of both sides;  x 2  2   (2 cos 4 )3  x 6  6  3 x 2 . 2  x 2  2   8 cos 3 4, x, x , x , x , , , Example: 48, ,  x6 , , 1,  3(2 cos 4 ) = 8 cos 3 4, x6, ,  x6 , , 1,  2(4 cos 3 4  3 cos 4 )  2 cos 3(4 )  2 cos 12 ., x6, , For A = 133 o , 2 cos, ,  x6 , , 1, x6, ,  8 cos 3 4  6 cos 4, , A, is equal to, 2, , (a)  1  sin A  1  sin A, (b)  1  sin A  1  sin A, , Solution: (c), , (c), , 1  sin A  1  sin A, , (d), , 1  sin A  1  sin A, , For A  133 o ,, , Hence,, , A,  66 .5 o , 2, , 1  sin A  sin, , sin, , A, A,  cos  0, 2, 2, , A, A,  cos, ......(i) and, 2, 2, , Subtract (ii) from (i) we get, 2 cos, , Example: 49, , If 2 tan A  3 tan B, then, , sin 2 B, , , 5  cos 2 B, , Example: 50, , 3, 3, tan B  t, 2, 2, , , , , , , 1, 2, , sin A , , 2t, , , , If 90 o  A  180 o and sin A , , (a), , Solution: (d), ,  2t , , , 1  t2 , 1  t2, 5  , 2, 1  t, , 4  6t 2, , , , t, , (d) tan( A  2 B), , (c) tan( A  B), , (Let tan B  t ), , 2  3t 2, , [AMU 2001], ,  sin 2 B , , 2t, 1t, , 2, , , cos 2 B , , 1  t2, 1  t2, ,  tan( A  B) ., , A, 4, , then tan, is equal to, 5, 2, , (b), 4, 4,  tan A   ,, 5, 3, , A, 2 ,, tan A , 2 A, 1  tan, 2, , ......(ii), , A,  1  sin A  1  sin A ., 2, , (b) tan( A  B), , 2 tan A  3 tan B  tan A , , A, A,  cos, 2, 2, , sin 2 B, is equal to, 5  cos 2 B, , (a) tanA – tanB, Solution: (b), , 1  sin A  sin, , 2 tan, , Let tan, , 3, 5, , (90 o  A  180 o ), , A, P, 2, , [AMU 2001], , (c), , 3, 2, , (d) 2

Page 22 :
22 Trigonometrical Ratios, Functions and, Identities, , , 1, 1, 4, 2P,  4 P 2  6 P  4  0  P   , 2  P   (impossible), , 2, 2, 3 1  P2, , So, P  2 i.e., tan, , Example: 51, , If tan  , , A,  2., 2, , 1, 1, and sin  , , then tan(  2  ) is equal to, 7, 10, , (a) 1, , Solution: (a), , (b) 0, , (c), , 1, 2, , (d), , 3, 4, , 2, 1, 1, 1, 3, 3, tan   , sin  ,  tan  ,  tan 2  =, , 1, 3, 7, 4, 10, 1, 9, 1 3, , 7, 4  4  21  1,  tan(  2  ) , 3, 25, 1, 28, , Example: 52, , If tan, , , 2, ,  t, then, , 1  t2, is equal to, 1  t2, , (b) sin , , (a) cos , , Solution: (a), , Example: 53, , 1  t2, 1  t2, , 1  tan 2, , =, 1  tan, , The value of, , 2, , , 2, , , , ( tan, , , 2, , (c) sec , , (d) cos 2, , , ,  t) = cos( 2 . )  cos  ., 2, , 2, , tan x, when ever defined never lie between, tan 3 x, , [Haryana CEE, , 1998; IIT 1992, 97], , (a), Solution: (a), , 1, and 3, 3, , Let, y , , (b), , 1, and 4, 4, , (c), , 1, and 5, 5, , (d) 5 and 6, , tan x, tan x, , tan 3 x, 3 tan x  tan 3 x, 1  3 tan 2 x, , 1,  tan 2 x, 1  3 tan 2 x, 3, y, , 1, 3  tan 2 x, 1  tan 2 x, 3, , Hence, y should never lie between, Example: 54, , If tan   t , then tan 2  sec 2 equal to, (a), , Solution: (a), , 1, and 3 whenever defined., 3, , 1t, 1t, , tan 2  sec 2 , , (b), , 1t, 1t, , [MP PET 1999], , (c), , 2t, 1t, , 2 tan , 1  tan 2 , , 1  tan 2  1  tan 2 , , Given tan   t   tan 2  sec 2 , , 2t, 1  t2, 2 t  1  t 2 (t  1)2, 1t, , , , =, ., 2, 2, 2, 2, 1t, 1t, 1t, 1t, 1t, , (d), , 2t, 1t

Page 23 :
Trigonometrical Ratios, Functions and Identities 23, Example: 55, , If sin 2  sin 2 , (a), , Solution: (b), , 1, 3, and cos 2  cos 2  , then cos 2 (   ) equal to, 2, 2, , 3, 8, , (b), , Given, sin 2  sin 2 , , 1, 2, , 5, 8, , 3, 4, , (c), , .......(i) and cos 2  cos 2 , , 3, 2, , [MP PET 2000], , (d), , .......(ii), 1 9, , 4 4, , Squaring and adding, (sin 2 2  cos 2 2 )  (sin 2 2  cos 2 2 )  2[sin 2 . sin 2  cos 2 . cos 2 ] ,  cos 2 . cos 2  sin 2 . sin 2 , , Example: 56, , If tan x , (a), , Solution: (b), , b, , then, a, , ab, , ab, , 2 sin x, , Given tan x , , 5, 1, 1,  cos( 2  2 ) ,  cos 2 (   )  ., 8, 4, 4, , ab, equal to, ab, , (b), , sin 2 x, b, , a, , Now, multiplying by, , 5, 4, , [MP PET 1990, 2002], , 2 cos x, , ab, ab, 1  b /a, 1 b /a, =, , , , ab, ab, 1 b /a, 1  b /a, , 1  tan 2 x in N'r and D'r =, , 2 cos x, , (c), , cos 2 x, , (d), , sin 2 x, , 1  tan x, 1  tan x, , , 1  tan x, 1  tan x, 2, , 1  tan x, 2, , 1  tan 2 x, , . 1  tan x, , cos 2 x, , 2, 1  tan 2 x, 2, , , 2, , 2 sin x, , =, 2, , cos 2 x . sec x, , 2 cos x, cos 2 x, , ., , 1.14 Maximum and Minimum Value of a cos + b sin., Let, , a  r cos , , ……..(i), , and b  r sin , , ……..(ii), , Squaring and adding (i) and (ii), then a 2  b 2  r 2 or, r  a 2  b 2,  a sin   b cos  = r(sin  cos   cos  sin  ) = r sin(   ), But, ,  1  sin   1 So,  1  sin(   )  1 ; Then  r  r sin(   )  r, , Hence,  a 2  b 2  a sin   b cos   a 2  b 2, Then the greatest and least values of a sin   b cos  are respectively, , Note : , , a 2  b 2 and  a 2  b 2 ., , sin 2 x  cosec 2 x  2, for every real x., ,  cos 2 x  sec 2 x  2, for every real x.,  tan 2 x  cot 2 x  2 , for every real x., Important Tips, Use of  (Sigma) and  (Pie) notation, , , sin( A  B  C)   sin A cos B cos C   sin A ,, , tan( A  B  C ) , , , ,  tan A   tan A, ., 1   tan A tan B, , sin   sin(   )  sin(  2  )  ......... n terms, , cos( A  B  C )   cos A   cos A sin B sin C ,, , (  denotes summation), (  denotes product)

Page 24 :
24 Trigonometrical Ratios, Functions and, Identities, sin[  (n  1) / 2] sin[n  / 2], , sin( / 2), , n 1 , nB, , sin A , B  sin, 2, 2, , , ., B, sin, 2, , n, or  sin( A  r  1B) , r 1, , , , n, cos[  (n  1) / 2] sin[n  / 2], cos   cos(   )  cos(  2  )  ......... n terms , or  cos( A  r  1B) , sin[  / 2], r 1, , , , sin A / 2  cos A / 2  2 sin / 4  A   2 cos A   / 4  ., , , , cos   cos   cos   cos(     )  4 cos, , , , sin   sin   sin   sin(     )  4 sin, , , , tan   2 tan 2  4 tan 4  8 cot 8  cot  ., , Example: 57, , If x  y cos, , 2, , Example: 58, , sin, , cos, ,  , 2, ,  , 2, , sin, , cos, ,  , 2, ,  , 2, , ., , ., , 2, 4,  z cos, , then xy  yz  zx , 3, 3, , (b) 0, , We have, , , 2, , , , (a) 1, Solution: (b), , , , n 1 , nB, , cos  A , B  sin, 2, 2, , , ., B, sin, 2, , [EAMCET 1994], , (c) 1, , (d) 2, , x, y, z, , ,   (say), 1 2 2, ,  xy  yz  zx  22  4 2  22  0, , x   , y  2, z  2  ;, , sec 8 A  1, equal to, sec 4 A  1, , (a), , [MP PET 1995], , tan 2 A, tan 8 A, , (b), , tan 8 A, tan 2 A, , (c), , cot 8 A, cot 2 A, , (d) None of these, , Solution: (b), , 2 sin 4 . A cos 4 A . sin 4 A sin 8 A . 2 sin 2 A . cos 2 A tan 8 A, 1  cos 8 A cos 4 A, 2 sin 2 4 A cos 4 A, =, ., , , ., , ., tan 2 A, cos 8 A 1  cos 4 A, cos 8 A 2 sin 2 2 A, cos 8 A . 2 sin 2 2 A, cos 8 A . 2 sin 2 2 A, , Example: 59, , If tan  , , Solution: (a), , sin , cos , a, , , then, equal to, 8, b, cos  sin 8 , , [WB JEE 1986], , (a) , , (a 2  b 2 )4  a, b ,  8, , 2, 2 b8, a, , a b, , (b) , , (a 2  b 2 )4  a, b ,  8, , 2, 2 b8, a, , a b, , (c) , , (a 2  b 2 )4  a, b ,  8, , 2, 2 b8, a , a b, , (d) , , (a 2  b 2 )4  a, b ,  8, , 2, 2 b8, a , a b, , Given , tan   a / b  cos 2 , sin   , , a, a b, 2, , 2, , 1  tan 2 , b 2  a2,  2, 2, 1  tan , b  a2, , ; cos   , , b, a  b2, 2, , , , , , a, b, , , , , 2, 2 4,  2,  2, 2 , 2 , a(a 2  b 2 )4, b(a 2  b 2 )4,  sin   cos    a  b    a  b  = 8 2, =  (a  b ),  8 2, 2, 1, /, 2, 2 1/2, 8, 8, 8, 8, 2, b, (, a, , b, ), a, (, a, , b, ), cos  sin  , a  b2, , , , b, a, , , , ,  2,  2, 2 , 2 ,  a b ,  a b , , b .,  a,  8  8, b, a, , 

Page 25 :
Trigonometrical Ratios, Functions and Identities 25, Example: 60, , The minimum value of 3 cos x  4 sin x  5 =, (a) 5, , Solution: (d), , [UPSEAT 1991], , (b) 9, , (c) 7, , (d) 0, , Minimum value of 3 cos x  4 sin x   3 2  4 2   5, Minimum value of 3 cos x  4 sin x  5  5  5  0 ., , Example: 61, , The greatest and least value of sin x cos x are, (a) 1,  1, , Solution: (b), Example: 62, , [UPSEAT 1975], , 1, 1, ,, 2, 2, , (b), , (c), , 1, 1, ,, 4, 4, , (d) 2, 2, , 1 sin 2 x 1, 1, 1, ,  ., [2 sin x cos x ]  sin 2 x ; 1  sin 2 x  1 ;, 2, 2, 2, 2, 2, , The value of sin   cos  will be greatest when, , [UPSEAT 1977, 83; RPET, , 1995], , (a)   30 o, Solution: (b), , (b)   45 o, , Let f (x )  sin   cos  ,  1  sin( , , , 4, , 2 sin( , , , 4, , (d)   90 o, , ), , 2 sin( , , )1   2 , , (c)   60 o, , , 4, , ), , 2, , If f (x ) is maximum then,, sin( , , Example: 63, , , 4, , )  1  sin, , , 2, ,   , , 4, ,  , , , 4, , , , , 2, ,  , , , 4, , ., , The maximum value of sin 2 x  3 cos 2 x is, (a) 3, , Solution: (b), , , , [Karnataka CET 2003], , (b) 4, , (c) 5, , (d) 7, , f (x )  4 sin 2 x  3 cos 2 x  sin 2 x  3 and 0 | sin x |  1, ,  Maximum value of sin 2 x  3 cos 2 x is 4., Example: 64, , If A  cos 2   sin 4  , then for all values of , , [UPSEAT 2001; IIT 1980; Roorkee 1992;, , EAMCET 1994], , (a) 1  A  2, Solution: (d), , (b), , 13,  A 1, 16, , (c), , A  cos 2 x  sin 4 x  cos 2   sin 2  sin 2 , ,  A  cos 2   sin 2 , Again, , [  sin 2   1 ], ,  A 1, , A  cos 2   sin 4   (1  sin 2  )  sin 4 , 3, , 1, 3 3, , A   sin 2     , 2, 4 4, , , Hence,, , Example: 65, , 3,  A 1., 4, , The value of 5 cos   3 cos( , , , 3, , )  3 lies between, , 3, 13, A, 4, 16, , (d), , 3,  A 1, 4

Page 26 :
26 Trigonometrical Ratios, Functions and, Identities, Solution: (d), , (b)  4 and 6, , (a)  4 and 4, 5 cos   3 cos( , , = [5 cos  , , , 3, , )  3 = 5 cos   3[cos  cos, , (c)  4 and 8, , , , (d)  4 and 10, , , ,  sin  . sin ]  3, 3, , 3, ,  13, , 3 3, 3, 3 3, sin    3, cos  , sin  ]  3 =  cos  ,  2, , 2, 2, 2, , , 2, , 2, 2, , , , , , ,    13    3 3    13 cos   3 3 sin    13    3 3 , , , , , , 2,  2   2 ,  2   2 ,  2, , , 2, ,  13, , 3 3, 7  , cos  , sin    7,  2, , 2, , ,  13, ,   7  3  , ,  2, , cos  , ,  13, , , 3 3, 3 3, cos  , sin    3  7  3   4  , sin    3  10, , , , 2, 2,  2, , , , So, the value lies between – 4 and 10., Example: 66, , sin, , (a), , Solution: (d), , sin, , , 14, , , 14, , (b), , . sin, , , 14, , 1, 16, , (c), , 1, 32, , 1, 64, , 2, , . sin, , 3, 5, 5 , 3 ,  , , 3, 5, 7 , 1, , , , , . sin,  1  sin  , . sin, . sin, . sin, . sin  ,  . sin  ,  = sin,   64 ., 14, 14, 14, 14, 14, 14, 14, 14, 14, , , , , , , , , , a2  b 2, 4  a2  b 2, , (b), ,  , 2, , equal to, , 4  a2  b 2, a2  b 2, , Given that, sin   sin   a ........(i), , and, , (c), cos   cos   b, , a2  b 2, 4  a2  b 2, , ......(ii), , Squaring, sin 2   sin 2   2 sin  sin   a 2 and cos 2   cos 2   2 cos  cos   b 2, Adding, 2  2(sin  sin   cos  . cos  )  a 2  b 2, a2  b 2  2,  2 cos(   )  a  b  2  cos(   ) , 2, 2, , 2, ,  (a 2  b 2 )  (a 2  b 2 ) tan 2, , , , (d), , 3 sin 5, 7, 9, 11, 13, ., . sin, . sin, . sin, . sin, 14, 14, 14, 14, 14, 14, , If sin   sin   a and cos   cos   b then tan, , (a), Soluton: (b), , 3, 5, 7, 9, 11, 13, . sin, . sin, . sin, . sin, . sin, is equal to, 14, 14, 14, 14, 14, 14, , 1, 8, , = sin, , Example: 67, , . sin, ,  , 2, ,  2  2 tan 2, , 4  a2  b 2, (   ), (   ),  tan 2,  tan, , 2, 2, 2, 2, a b, ,  , 2, , (   ), a2  b 2  2, 2, , , (   ), 2, 1  tan 2, 2, 1  tan 2, ,  2  2 tan 2, , 4  a2  b 2, a2  b 2, ,  , 2, , (d), , 4  a2  b 2, a2  b 2

Page 27 :
Trigonometrical Ratios, Functions and Identities 27, Trick : Put  , ,  tan, , , 2, , ,   0 o , then a  1  b, ,  , 2, , Again putting  , Example: 68, , , 4, ,   , we get tan, ,  , 2, ,  0 , which is given by (b)., , The maximum value of 3 cos   4 sin  equal to, (a) 3, , Solution: (c), ,  1, which is given by (a) and (b)., , (b) 4, , Maximum value of 3 cos   4 sin  is, , [MP PET 2002; UPSEAT 1990], , (c) 5, , (d) None of these, , 32  4 2  5 ., , 1.15 Conditional Trigonometrical Identitites., We have certain trigonometric identities. Like, sin 2   cos 2   1 and 1  tan 2   sec 2  etc., Such identities are identities in the sense that they hold for all value of the angles which, satisfy the given condition among them and they are called conditional identities., If A, B, C denote the anlges of a triangle ABC, then the relation A + B + C =  enables us to, establish many important identities involving trigonometric ratios of these angles., (1) If A + B + C = , then A + B =  – C, B + C =  – A and C + A =  – B., (2) If A + B + C = , then sin( A  B)  sin(  C)  sin C, Similarly, sin( B  C)  sin(  A)  sin A and sin( C  A)  sin(  B)  sin B, (3) If A  B  C   , then cos( A  B)  cos(  C)   cos C, Similarly, cos(B  C)  cos(  A)   cos A and cos(C  A)  cos(  B)   cos B, (4) If A + B + C = , then tan( A  B)  tan(  C)   tan C, Similarly, tan( B  C)  tan(  A)   tan A and tan( C  A)  tan(  B)   tan B, (5) If A  B  C   , then, , AB  C, BC  A, CA  B, and, and,  ,  ,  , 2, 2 2, 2, 2 2, 2, 2 2, ,  A B,  C , C,  A B,  C , C, sin ,   sin     cos   , cos ,   cos     sin   ,,  2 , 2 2, 2,  2 , 2 2, 2,  A B,  C , C, tan ,   tan     cot  ,  2 , 2 2, 2, All problems on conditional identities are broadly divided into the following three types, 1. Identities involving sine and cosine of the multiple or sub-multiple of the angles involved, , Working Method

Page 28 :
28 Trigonometrical Ratios, Functions and, Identities, , Step (i) : Use C  D formulae., Step (ii) : Use the given relation (A + B + C = ) in the expression obtained in step-(i) such, , that a factor can be taken common after using multiple angles formulae in the remaining term., Step (iii) : Take the common factor outside., Step (iv) : Again use the given relation (A + B + C = ) within the bracket in such a manner, so that we can apply C  D formulae., Step (v) : Find the result according to the given options., 2. Identities involving squares of sine and cosine of multiple or sub-multiples of the angles, involved, , Working Method, Step (i) : Arrange the terms of the identity such that either sin 2 A  sin 2 B  sin( A  B). sin( A  B), or cos 2 A  sin 2 B  cos( A  B). cos( A  B) can be used., Step (ii) : Take the common factor outside., Step (iii) : Use the given relation (A  B  C   ) within the bracket in such a manner so that, we can apply C  D formulae., Step (iv) : Find the result according to the given options., 3. Identities for tangent and cotangent of the angles, , Working Method, Step (i) : Express the sum of the two angles in terms of third angle by using the given, relation ( A  B  C   ) ., Step (ii) : Taking tangent or cotangent of the angles of both the sides., Step (iii) : Use sum and difference formulae in the left hand side., Step (iv) : Use cross multiplication in the expression obtained in the step (iii)., Step (v) : Arrange the terms as per the result required., Example: 69, , Solution: (a), , If A  B  C   , then cos 2 A  cos 2 B  cos 2 C equal to, (a) 1  2 sin A sin B cos C, , (b) 1  2 cos A cos B sin C, , (c) 1  2 sin A sin B cos C, , (d) 1  2 cos A cos B sin C, , cos 2 A  cos 2 B  cos 2 C  cos 2 A  (1  sin 2 B)  cos 2 C, ,  1  [cos 2 A  sin 2 B]  cos 2 C  1  cos( A  B) cos( A  B)  cos 2 C,  1  cos   C) cos( A  B)  cos 2 C  1  cos C[cos( A  B)  cos C],  1  cos C[cos( A  B)  cos{  ( A  B)}]  1  cos C[cos( A  B)  cos( A  B)], ,  1  cos C[2 sin A sin B]  1  2 sin A sin B cos C .

Page 29 :
Trigonometrical Ratios, Functions and Identities 29, Example: 70, , sin 2 A  sin 2 B  sin 2C, equal to, sin A  sin B  sin C, , (a), , Solution: (a), , cos A cos B sin C, A, B, C, sin sin cos, 2, 2, 2, , sin A sin B cos C, A, B, C, cos cos sin, 2, 2, 2, , (b), , (c) , , 2 sin( A  B) cos( A  B)  sin 2C, (sin 2 A  sin 2 B)  sin 2C, =, (sin A  sin B)  sin C,  AB,  AB, 2 sin,  cos ,   sin C,  2 ,  2 , , =, , =, , =, , cos A cos B sin C, A, B, C, sin sin cos, 2, 2, 2, , (d) , , sin A sin B cos C, A, B, C, cos cos sin, 2, 2, 2, , 2 sin C cos( A  B)  2 sin C cos C, C, C,   C ,  AB, 2 sin,  cos ,   2 sin cos, 2, 2,  2 ,  2 , , C, C, , ,  sin C  2 sin cos, , , 2, 2, , , , A, , B, (, A, , B, ), , , sin C / 2  sin , ,   cos, , 2 , 2 , 2, , 2 sin C[cos( A  B)  cos C], C   A B,  A B , 2 cos cos     cos   , 2  2 2,  2 2 , , 2 sin C[2 cos A cos B], 2 sin C[cos( A  B)  cos( A  B)], cos A cos B sin C, =, =, ., A, B, C, C, A, B, , , C   A B,  A B , sin sin cos, 2 cos cos     cos    2 cos  2 sin sin , 2, 2, 2, 2 , 2, 2, 2  2 2,  2 2 , , Trick :  sin 2 A  sin 2B  sin 2C  4 cos A cos B sin C, and sin A  sin B  sin C  4 sin, , A, B, C, sin cos  sin 2 A  sin 2 B  sin 2C  cos A cos B sin C ., 2, 2, 2, A, B, C, sin A  sin B  sin C, sin, , Example: 71, , (c) tan, , , 2, , , 2, ,  tan,  tan, , , 2, , , 2, ,  tan,  tan, , , 2, , , 2, ,  tan, , tan, , , 2, ,  tan, , , 2, ,  tan, , , 2, , , 2, ,   tan, , , 2, ,  tan, , cos, , 2, , , , , 2, , , , tan, , , 2, , , 2, , tan, , , tan, , 2, , , 2, , , , (b) tan, , 2, , tan, , , , , , , , , , tan  tan tan  tan tan  1, 2, 2, 2, 2, 2, 2, , (d) None of these, , 2, ,    ,    tan      tan   0, 2,  2 2 2, , , , . tan, , , 2, , . tan, , , 2, , 0 , , tan, , , 2, ,  tan, , , 2, ,  tan, , , 2, ,  tan, , , 2, , . tan, , , 2, , . tan, , , 2, , If A  B  C   , then cos 2 A  cos 2B  cos 2C equal to, (a) 1  4 cos A cos B sin C, , Solution: (c), , 2, , [IIT 1979], , We have       2 , , , Example: 72, , sin, , If       2 , then, (a) tan, , Solution: (a), , 2, , (b) 1  4 sin A sin B cos C, , [EAMCET 1982], , (c) 1  4 cos A cos B cos C (d) None of these, , cos 2 A  cos 2B  cos 2C = 2 cos( A  B). cos( A  B)  (2 cos 2 C  1) =  1  2 cos C. cos( A  B)  2 cos 2 C, = 1  2 cos c[cos( A  B)  cos( A  B)] = 1  4 cos A. cos B. cos C, , Example: 73, , If A  B  C  180 o , then, , (a) 8 sin, , Solution: (b), , A, B, C, sin sin, 2, 2, 2, , sin 2 A  sin 2 B  sin 2C, equal to, cos A  cos B  cos C  1, , (b) 8 cos, , A, B, C, cos cos, 2, 2, 2, , (c) 8 sin, , A, B, C, cos cos, 2, 2, 2, , (d) 8 cos, , sin 2 A  sin 2 B  sin 2C, 2 sin( A  B) . cos( A  B)  2 sin C cos C, 2 sin C cos( A  B)  2 cos C sin C, =, , C, AB, C, cos A  cos B  cos C  1 2 cos A  B cos A  B  1  2 sin 2 C  1, 2 sin cos,  2 sin 2, 2, 2, 2, 2, 2, 2, , =, , 2 sin C[cos( A  B)  cos( A  B)], 4 sin A sin B sin C, =, A, B, C, C, ( A  B), ( A  B) , 4 sin sin sin, 2 sin cos,  cos, , 2, 2, 2, 2 , 2, 2 , , A, B, C, sin sin, 2, 2, 2

Page 30 :
30 Trigonometrical Ratios, Functions and, Identities, , , Example: 74, , 4  2 sin, , A, A, B, B, C, C,  cos  2 sin cos  2 sin cos, 2, 2, 2, 2, 2, 2  8 cos A cos B cos C ., A, B, C, 2, 2, 2, 4 sin sin sin, 2, 2, 2, , If A  B  C  180 o , then the value of (cot B  cot C)(cot C  cot A)(cot A  cot B) will be, (a) sec A sec B sec C, , Solutio: (b), , cot B  cot C , , (b) cosec A cosec B cosec C, , (c) tan A tan B tan C, , (d) 1, , sin C cos B  sin B cos C, sin(B  C) sin(180 o  A), sin A, =, , , sin B. sin C, sin B. sin C, sin B. sin C, sin B. sin C, , Similarly, cot C  cot A , , sin B, sin C, and cot A  cot B , sin C. sin A, sin A sin B, , Therefore, (cot B  cot C)(cot C  cot A)(cot A  cot B), =, , Example: 75, , sin A, sin B, sin C, ., .,  cosec A.cosec B.cosec C ., sin B . sin C sin C. sin A sin A sin B, , If A  B  C  180 o , then the value of cot, , (a) 2 cot, , Solution: (c), , A, B, C, cot cot, 2, 2, 2, , A  B  C  180 o , , , , (b) 4 cot, , A, B, C,  cot  cot, will be, 2, 2, 2, , A, B, C, cot cot, 2, 2, 2, , (c) cot, , A, B, C, cot cot, 2, 2, 2, , (d) 8 cot, , A, B, C, cot cot, 2, 2, 2, , A B, C,   90 o , 2 2, 2, , C,  A B, , cot     cot  90 o   or, 2, 2, 2, , , , , A, B, . cot  1, C, 1, 2, 2,  tan , B, A, C, 2, cot  cot, cot, 2, 2, 2, , cot, , A, B, C, B, A, A, B, C, C, B, A, , , or  cot . cot  1  cot  cot  cot ; cot . cot . cot  cot  cot  cot, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, , , , Example: 76, , If A, B, C are angles of a triangle, then sin 2 A  sin 2B  sin 2C is equal to, (a) 4 sin A cos B cos C, , Solution: (d), , (b) 4 cos A, , (c) 4 sin A cos A, , [MP PET 2003], , (d) 4 cos A cos B sin C, , sin 2 A  sin 2 B  sin 2C  2 sin A cos A  2 cos( B  C) sin(B  C), , [ A  B  C   , B  C    A, cos(B  C)  cos(  A), cos(B  C)   cos A, sin(B  C)  sin A], = 2 cos A[sin A  sin(B  C)] = 2 cos A[sin(B  C )  sin(B  C)] = 2 cos A.2 cos B. sin C  4 cos A. cos B. sin C, Trick: First put A  B  C  60 o , for these values. Options (a) and (b) satisfies the condition., Now put A  B  45 o and C  90 o , then only (d) satisfies., Hence (d) is the answer., Example: 77, , Solution: (c), , In any triangle ABC sin 2, , A, B, C,  sin 2  sin 2, is equal to, 2, 2, 2, , [MP PET 2003], , (a) 1  2 cos, , A, B, C, cos cos, 2, 2, 2, , (b) 1  2 sin, , A, B, C, cos cos, 2, 2, 2, , (c) 1  2 sin, , A, B, C, sin sin, 2, 2, 2, , (d) 1  2 cos, , A, B, C, cos sin, 2, 2, 2, , Trick: For A  B  C  60 o only option (c) satisfies the condition.

Page 31 :
Trigonometrical Ratios, Functions and Identities 31, , Important Tips, , , Method of componendo and dividendo, If, , p a,  , then by componendo and dividendo, q, b, , p q ab, , p q, ab, , We can write, , Example: 78, , q p ba, , q  p b a, , If tan   cos  . tan  then tan 2, , (a), , Solution: (a), , or, , sin(   ), sin(   ), , , 2, , (b), , The given relation is, , or, , p q, ab, , p q ab, , or, , q  p b a, ., , q p ba, , equal to, sin(   ), sin(   ), , (c), , cos(   ), cos(   ), , (d), , cos(   ), cos(   ), , (d), , nm, nm, , tan , 1, , tan  cos , , Applying componendo and dividendo rule, then, tan   tan  1  cos , , , tan   tan  1  cos , , Example: 79, , m n, m n, , (b), , (c), , m n, nm, , m cos(   ), , n cos(   ), , cot  cos  , , m n, ., nm, , If cosec  , , pq,   , , then cot    , p q, 4 2, , (a), , Solution: (b), , sin(   ), ,  tan 2 ., sin(   ), 2, , m n, m n, , By componendo and dividendo rule,, , Example: 80, , , , If m cos(   )  n cos(   ) , then cot  cot  equal to, (a), , Solution: (c), , , , 2 sin 2, sin(   ), 2, , , sin(   ) 2 cos 2 , 2, , p, q, , Given, co sec , , (b), , m n, 2 cos  cos , m  n cos(   )  cos(   ), , , , m  n  2 sin  sin , m  n cos(   )  cos(   ), , q, p, , [EAMCET 2001], , (c), , (d) pq, , pq, , pq, 1, pq, , , ,, p q, sin , p q, 2, , , , ,  cos 2  sin 2 , 1  sin , p q  p q, p, , , Apply componendo and dividendo,,  , , , 1  sin , p q  p q, q,  cos  sin , 2, 2 , , 2, , , , p,  p,  q,  1  tan  / 2 , 2 , 2 ,  1  tan  / 2   q  tan  4  2   q  cot  4  2   p, , , , , , 

Page 32 :
32 Trigonometrical Ratios, Functions and, Identities, , Note :, ,   , cot    , 4 2, , q,   , only if cot     0 ., p, 4 2, , ***