Page 1 :
CIRCLE, , CIRCLE, 1. DEFINITION, Circle is locus of a point which moves at a constant distance from a fixed point . This constant distance is called, radius of the circle and fixed point is called centre of the circle., , 2. STANDARD FORMS OF EQUATION OF A CIRCLE, 2.1, , General Form, The general equation of a circle is, x2 + y2 + 2gx + 2fy + c = 0,, , where g,f,c are constants., , 1,  1, , For this circle, Centre = ( – g , –f) =   coef. of x,  coef. of y  , Radius =, 2,  2, , , g2  f 2  c, , Note :, (i) The above equation represents,  a real circle if, , g2 + f 2 > c, ,  a point circle if, , g2 + f2 = c, ,  an imaginary circle if, , g2 + f2 < c, , (ii) In the above equation,  If c = 0  the circles passes through the origin,  If f = 0  the centre is on x-axis,  If g = 0  the centre is on y-axis, (iii) The general eqaution of second degree ax2 + by2 + 2hxy + 2gx + 2fy + c = 0 represents a circle if, a = b  0 and h = 0., , Ex.1, , Find the radius of the circle x2 + y2 + 4x – 6y + 1 = 0., , Sol., , Here, , x2 + y2 + 4x – 6y + 1 = 0, , on comparing from general eqn., 2g = 4, , , r=, , , , g = 2,, , 2f = –6, ,  f = –3,, , c=1, , g2  f 2  c  4  9  1  12  2 3, , Ex.2, , If (4, –2) is the one extremity of diameter to the circle x2 + y2 – 4x + 8y – 4 = 0 then find its other extremity., , Sol., , Centre of circle is (2, –4). Let the other extremity is (h, k), , , ,  4h,  2  k ,  2   2,  2    4, , , , , ,  (h, k) = (0 , –6), , Ex.3, , If y = 2x + m is a diameter to the circle x2 + y2 + 3x + 4y – 1 = 0, then find m, , Sol., , Centre of circle = ( –3/2 , –2). This lies on diameter y = 2x + m, , , , – 2 = –3/2 × 2 + m, , , , m=1, 56

Page 2 :
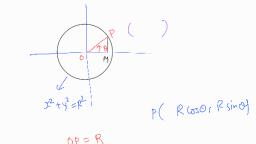
CIRCLE, , 2.2, , Central Form, If ( h, k) be the centre and 'a' be the radius of a circle, then its equation is, ,  x  h   y  k , 2, , 2, ,  a2, , Note :,  If the centre is origin, then the eqation of the circle is x2 + y2 = r2 (simplest form),  If a = 0 than circle is called point circle and its equation is ( x–h)2 + ( y–k)2 = 0, Ex.4, , Find the equation of a circle whose centre is (3, –1) and radius is 3, , Sol., , (x – 3)2 + (y + 1)2 = 32, ,  x2 – 6x + 9 + y2 + 2y + 1 = 9,  x2 + y2 – 6x + 2y + 1 = 0, Ex.5, , Find the equation of a circle with centre at the origin and which passes through the point ( , ) ., , Sol., , Here radius =, , 2.3, , Diameter Form, ,  2  2 ; so the required equation is x2 + y2 = 2 + 2, , If (x1, y1) and (x2, y2 ) are end points of a diameter of a circle then its equation is, (x – x1) (x – x2) + (y – y1) (y – y2) = 0, 2.4, , Parametric Equation of a Circle, (a) The parametric equations of a circle x2 + y2 = a2 are, x = acos , y = asin., Hence parametric coordinates of any point lying on the circle x2 + y2 = a2 are, y, , (acos, asin), , (acos, asin), , (b) The parametric equations of the circle (x – h)2 + (y – k)2 = a2 are, x = h + a cos , y = k + asin., , a, , O, , x, , Hence parametric coordinates of any point lying on the circle are, (h + acos, k + asin), (c) Parametric equations of the circle x2 + y2 + 2gx + 2fy + c = 0 is, x=–g+, , g2  f 2  c cos,, , y=–f+, , g2  f 2  c sin, , Ex.6, , Find the parametric coordinates of any point of the circle x2 + y2 + 2x – 3y – 4 = 0, , Sol., , 3, , Centre =  1, , 2, , , radius =, , 1, , 4, 7, 4 , 9, 3, ,  Parametric coordinates of any point are (–1 +, , 7, 7, 3, cos ,, + sin), 3, 3, 2, 57

Page 3 :
CIRCLE, , 3. EQUATION OF A CIRCLE IN SOME SPECIAL CASES, y, , (i), , Which touches both axes : The equation of a circle with radius 'a' touching both coordinate, , (a, a), , axes is given by, x, , (x ± a)2 + (y ± a)2 = a2, (ii), , O, , Which touches x-axis : The equation of a circle with radius 'a' touching x-axis at a distance h from the origin, is, , y, , (x – h)2 + (y – a)2 = a2, Note : The equation of a circle with radius 'a' touching x-axis at the origin is, , a, , x2 + (y ± a)2 = a2, , (iii), , 2, , h, , O, , x, , 2, , x + y ± 2ay = 0, , Which touches y-axis : The equation of a circle with radius 'a' touching y-axis at a distance k from the origin is, y, , (x – a)2 + (y – k)2 = a2, Note : The equation of a circle with radius 'a' touching y-axis at the origin is, (x ± a)2 + y2 = a2, , , , x2 + y2 ± 2ax = 0, , a, k, , x, , O, , Ex.7 If the circle x2 + y2 + 2gx + 2fy + c = 0 touches x-axis, then find the value of c., Sol. Touches x-axis, hence radius = ordinate of centre., Hence, , g2  f 2  c  (  f ) or g2 = c., , 4. EQUATIONS OF THE CIRCUMCIRCLES, 4.1, , Circumcircle of a triangle, If we are given sides of a triangle, then first of all we should find its vertices. Observing to the equations of the, sides or coordinates of the vertices, if the triangle is right angled then its hypotenuse will be a diameter of the, circumcircle. So using diameter form we can easily write the required equation. If the triangle is not right angled,, then we find the required equation using general form., , 4.2, , Circumcircle of a quadrilateral, If a quadrilateral is a rectangle or a square, then the diagonals will be diameters of the circumcircle. Hence, finding the vertices of a diagonal, we can easily determine the required equations., , Ex.8, , Find the equation of the circle passing through the origin and cutting intercepts a, b from coordinate axes., , Sol., , If the circle meets the axes at A and B, then, A  (a, 0), B  (0, b), AOB = 90°, so AB is a diamete of the circle, Hence its equation will be, (x – a) (x – 0) + (y – 0) (y – b) = 0, , , x2 + y2 – ax – by = 0, 58

Page 4 :
CIRCLE, , 5. INTERCEPT ON A LINE OR LENGTH OF A CHORD, The length of a chord AB of a circle (or the intercept made by a circle on a line) is given by, , AB  2 a 2  p 2, where 'a' is the radius of the circle and 'p' is the length of the perpendicular from its centre on the chord., In particular the circle x2 + y2 + 2gx + 2fy + c = 0 cuts, , (i), , intercept on x-axis  2 g2  c, , 2, , C, a, , 2 f -c, , p, 2, , (ii), , intercept on y-axis  2 f 2  c, , A, , M, , 2 g -c, , B, , O, , Ex.9 Find the length of intercept on y-axis, by a circle whose diameter is the line joining the point (–4, 3) and (12, –1)., Sol. Here equation of the circle (x + 4) (x – 12) + (y – 3) (y + 1) = 0, or, , x2 + y2 – 8x – 2y – 51 = 0, , Hence intercept on y-axis, = 2 f 2  c  2 1  ( 51)  4 13, , 6. POSITION OF A POINT AND LINE WITH RESPECT TO A CIRCLE, 6.1, , Position of a point, A point (x 1 , y1) lies outside, on or inside a circle S  x 2 + y2 + 2gx + 2fy + c = 0 according as, S1  x12 + y12 + 2gx1 + 2fy1 + c is positive, zero or negative. So,  S1 > 0  (x1, y1) is outside the circle,  S1 = 0  (x1, y1) is on the circle,  S1 < 0  (x1, y1) is inside the circle, , 6.2, , Position of a line, Let L = 0 be a line and S = 0 be a circle. If 'a' be the radius of the circle and 'p' be the length of the perpendicular, from its centre on the line, then,  p > a  line is outside the circle,  p = a  line touches the circle, p, ,  p < a  line is a chord of the circle, a, , C, ,  p = 0  line is a diameter of the circle, , 59

Page 5 :
CIRCLE, , 7. CONDITION OF TANGENCY, A line L = 0 touches the circle S = 0, if length of perpendicular drawn from the centre of the circle to the line, is equal to radius of the circle i.e., p = r. This is the condition of tangency for the line L = 0., The line y = mx + c touches the circle x2 + y2 = a2 if c = ± a 1 m 2, Thus, for every value of m, the line y = mx ± a 1 m 2,   am, a, , ,, is a tangent of the circle x2 + y2 = a2 and its point of contact is , 2, 1  m2,  1 m, , , , , , , Note :,  If a2 (1 + m2) – c2 > 0 line will meet the circle at real and different points.,  If c2 = a2 (1 + m2) line will touch the circle.,  If a2 (1 + m2) – c2 > 0 line will meet circle at two imaginary points., Ex.10 If the line y = mx + c touches the circle x2 + y2 = 4y then find c., Sol. Centre of the circle = (0, 2), radius = 2. So condition of tangency, c 2, 2, p = a ,  c = 2 (1  m 2  1), m2  1, Ex.11 Find the point at line y = x +, , 2, 2, 2, 2a touches the circle x + y = a ., , Sol. The line y = mx + a 1  m 2 touches the circle x2 + y2 = a2 at the point, ,   am, a, , , ,, , , 2, 1  m2 ,  1 m, a a , , ,, Here m = 1, a = a, so the required point is , 2,  2, , 8. EQUATION OF THE TANGENT AND NORMALS AT A POINT, 8.1, , Equation of a tangent, The equation of the tangent at a point (x1, y1) of a circle, x2 + y2 + 2gx + 2fy + c = 0 is, xx1 + yy1 + g(x + x1) + f(y + y1) + c = 0 = T, , 8.2, , Equation of the Normal, The equation of the normal at the point (x1, y1) to the circle, x2 + y2 + 2gx + 2fy + c = 0 is , , x  x1 y  y1, , x1  g y1  f, , Note : For the circle x2 + y2 = a2 it becomes, , x, y, , x1 y1, 60

Page 6 :
CIRCLE, , 8.3, , Length of the tangent, The length of the tangent drawn from a point P(x1, y1) to the circle, S  x2 + y2 + 2gx + 2fy + c = 0 is given by PQ = PR =, , S1, , where S1 = x12 + y12 + 2gx1 + 2fy1 + c, Also area of the quadrilateral PQCR = r S1 and angle between tangents PQ and PR i.e., QPR = 2tan–1, 8.4, , r, S1, , Equation of the pair of tangents, From a given point P(x1, y1), two tangents PQ and PR can be drawn to a circle, S  x2 + y2 + 2gx + 2fy + c = 0. Their combined equation is given by SS1 = T2, , Ex.12 Write the equation of the tangent to the circle (x – 1)2 + (y + 2)2 = 10 at the point (2, 1), Sol. The eqaution of the given circle can be written as, x2 + y2 – 2x + 4y – 5 = 0., So the equation of the tangent at (2, 1) will be, x(2) + y(1) – (x + 2) + 2(y + 1) – 5 = 0, , , , x + 3y – 5 = 0, , Ex.13 Find the equation of the normal to the circle x2 + y2 + 6x + 8y + 1 = 0 passign through (0, 0), Sol. Centre of the circle = (–3, –4). So the normal is a line passing through (0, 0) and (–3, –4). Consequently its, equation is, y – 0 =, , 4, ( x  0), 3, , , , 4x – 3y = 0, , Ex.14 Two tangents PQ and PR drawn to the circle x2 + y2 – 2x – 4y – 20 = 0 from point P(16, 7). If the centre, of the cirlce is C then find the area of quadrilateral PQCR., Sol. Area PQCR = 2PQC = 2 ×, , 1, L×r, 2, , Q, L, , r, , Where L = length of tangent and r = radius of circle., , C, , P, , L=, , S1 and r =, , 1  4  20  5, R, , Hence the required area = 75 sq. units., , Ex.15 A pair of tangents are drawn from the origin to the circle x2 + y2 + 20 (x + y) + 20 = 0. Then find equation of the pair, of tangent., Sol. Equation of pair of tangents is given by SS1 = T2., or S = x2 + y2 + 20(x + y) + 20,, , S1 = 20, , ,, , T =10(x + y) + 20 = 0, ,  SS1 = T2,  20 {x2 + y2 + 20(x + y) + 20} = 102 (x + y + 2)2, ,  4x2 + 4y2 + 10xy = 0, ,  2x2 + 2y2 + 5xy = 0, 61

Page 7 :
CIRCLE, , 9. DIRECTOR CIRCLE, The locus of the point of intersection of two perpendicular tangents of a circle is called the director circle of that, circle., The equation of the director circle of x2 + y2 = a2, , is x 2  y 2  2a2, , It may be easily seen that,  Centre of the director circle = centre of the given circle.,  Radius of the director circle =, , 2 (radius of the given circle), , 10. CHORD OF CONTACT, The chord joining the two points of contact of tangents to a circle drawn from any point P is called chord of contact, of P with respect to the given circle., Let the given point is P(x1 , y1) and the circle is S = 0 then equation of the chord of contact is, T = xx1 + yy1 + g (x + x1) + f(y + y1) + c = 0, , Q, S=0, , Note:, ,  Area of triangle PQR =, , P, , Chord of, contact, ,  Length of chord of contact = 2 r 2  p2, a(x12  y12  a2 )3 / 2, x12  y12, , (x1, y1), R, , Ex. 16 Find the distance between the chord of contact with respect to point (0, 0) and (g, f) of circle, x2 + y2 + 2gx + 2fy + c = 0., Sol. Chord of contact with respect to (0, 0), gx + fy + c = 0, , ....(i), , Chord of contact with respect to (g, f), gx + fy + g(x + g) + f(y + f) + c = 0, , , 2gx + 2fy + g2 + f2 + c = 0, , , , gx + fy +, , 1 2 2, (g + f + c) = 0, 2, , ....(ii), , 1 2, (g  f 2  c )  c, g2  f 2  c, 2, , Distance betwen (i) and (ii) is =, g2  f 2, 2 g2  f 2, , 11. POLE & POLAR, Let P(x1, y1) be any point inside or outside the circle. Draw chords AB and A' B' pasing through P. If tangent to the, circle at A and B meet at Q (h, k), then locus of Q is called polar of P.w.r.t. circle and P is called the pole and if, tangent to the circle at A' and B' meet at Q', then the straigt line QQ' is polar with P' as its pole., Q', , Q(h, k), , B', , A, A', , Polar, , Pole, P(x1, y1), , B, Q', , Polar, , A', P(x1, y1) Pole, , B, , A, , B', , Q(h, k), , 62

Page 8 :
CIRCLE, , 11.1, , Equation of polar,  Equation of polar of the pole P(x1, y1) w.r.t. x2 + y2 = a2 is, xx1 + yy1 = a2,  Equation of polar of the pole (x1, y1) w.r.t. circle x2 + y2 + 2gx + 2fy + c = 0 is, xx1 + yy1 + g(x + x1) + f(y + y1) + c = 0, , 11.2, , Coordinates of pole, ,  Aa 2 Ba 2 , , ,  Pole of polar Ax + By + C = 0 w.r.t. circle x2 + y2 = a2 is   C , C , , ,  Pole of polar Ax + By + C = 0 with respect to circle x2 + y2 + 2gx + 2fy + c = 0 is given by the equation, x 1  g y1  f gx 1  fy1  c, , , A, B, C, , 11.3, , Conjugate points and Conjugate lines, (i) Conjugate points :- Two points are called conjugate points with respect to a circle if each point lies on the, polar of the other point with respect to the same circle., (ii) Conjugate lines :- Two lines are called conjugate lines with respect to a circle if the pole of each line lies on, the other line., , Ex.17, , Find the equation of polar of point ( 4, 4) with respect to circle ( x – 1)2 + ( y – 2)2 = 1., (x – 1)2 + ( y – 2)2 = 1, , Sol., , x2 + y2 – 2x – 4y + 4 = 0, equation of polar of point ( 4 , 4) is, 4x + 4y – (x + 4) – 2( y + 4) + 4 = 0, , , 3x – 2y – 8 = 0, , Ex.18, , Find the pole of the line, , Sol., , Let the pole is ( h , k), , x y,   1 with respect to circle x2 + y2 = c2 ., a b, , Hence polar of this pole is xh + yk – c2 = 0, x y, but polar is   0, a b, comparing the coefficient of x and y, h, k, c 2, c2, c2, , , h, ,k, 1/ a  1/ b  1, a, b, , .....(1), .....(2), , 12. CHORD WITH A GIVEN MIDDLE POINT, The equation of the chord of the circle S = x 2 + y 2 + 2gx + 2fy + c = 0 whose mid-point is, (x1, y1) is given by T = S1, i.e. xx1 + yy1 + g(x + x1) f(y + y1) = x12 + y12 + 2gx1 + 2fy1, In particular, the equation of the chord of the circle x2 + y2 = a2 whose middel point is, (x1 , y1) is T = S1, i.e., xx1 + yy1 = x12 + y12, , O, A, , P(x1, y1), , B, , 63

Page 9 :
CIRCLE, 2, , 2, , Ex.19, , Find the equation of chord of the circle x + y = 8x bisected at the point ( 4 , 3)., , Sol., , T = S1  x (4) + y(3) – 4 (x + 4) = 16 + 9 – 32, , , , 3y – 9 = 0  y = 3, , 13. DIAMETER OF A CIRCLE, The locus of middle points of a system of parallel chords of a circle is called the diameter of that circle. The, diameter of the circle x2 + y2 = r2 corresponding to the system of parallel chords y = mx + c is x + my = 0, , diameter, , y = mx + c, , Note :  Every Diameter passes through the centre of the circle.,  A diameter is perpendicular to the system of parallel chords., Ex.20, , Find the diameter of the circle x2 + y2 – 4x + 2y – 11 = 0 corresponding to a system of chords parallel to the line, x – 2y + 1 = 0., , Sol., , Centre of the circle = ( 2, –1)., The equation of the line perpendicular to chord x – 2y + 1 = 0 is 2x + y + k = 0, Since the line passes through the point ( 2, 1). So k = –3, The equation of diameter is 2x + y – 3 = 0, , 14. FAMILY OF CIRCLES, 14.1, , If S = 0 and S' = 0 are two intersecting circles, the S +  S' = 0 (  –1) represents family of circles passing, throguh intersection points of S = 0 and S' = 0 (  being parameter), S + S' = 0, A, , S=0, , 14.2, , B, , S'=0, , If S = 0 and L = 0 represent a circle and a line, then S + L = 0 represent family of circles passing through, intersection points of circle S= 0 and line L = 0 (  being parameter), S + L=0, , L=0, , S=0, , 14.3, , Family of circles touching a line ax + by + c = 0 at (x1 , y1 ) on it, is, (x – x1)2 + (y –y1)2 +  (ax + by + c) = 0, 64

Page 12 :
CIRCLE, , Ex.25, , A circle with radius 5 touches another circle x2 + y2 – 2x – 4y – 20 = 0 at point (5, 5). Find its eqaution., , Sol., , The centre of the given circle C1  (1, 2) and radius = 1  4  20  5 . Since the radii of two circles are equal so, they touch externally. If C2(h, k) be the centre of the required circle then the point of contact (5, 5) is the mid point, of C1C2. Hence C2  (9, 8) and the reqd. eqn will be (x – 9)2 + (y – 8)2 = 25,  x2 + y2 – 18x – 16y + 120 = 0 a, , 18. RADICAL AXIS & RADICAL CENTRE, 18.1, , Radical Axis, The radical axis of two circle is the locus of a point, which moves in such a way that the lengths of the tangents, drawn from it to two given circles are equal. The equation of radical axis of two circle S = 0 and S' = 0 is written, as S – S' = 0 i.e., 2(g1 – g2) x + 2(f1 – f2) y + c1 – c2 = 0, A, , Q, , axis, , P, , C2, , C1, , Note :  Radical axis biscets every common tangents of two circles.,  Radical axis of two circles is perpendicular to the line joining their centres.,  If two circles intersect a third circle orthogonally, then their radical axis will passes through the centre of third, circle.,  Radical axis of three circle, taken two at a time meet at a point provided the centre of the circle are not, collinear.,  If two circles intersect at two points then their radical axis coincides with their common chord. Also if they, touch each other then it coincides with their common tangent at their point of contact., 18.2, , Radical Centre, The point where the radical axis of three given circles taken in pairs meet, is called the radical centre of those, three circles., , C, , Thus the length of the three tangents drawn from the radical centre on the three circles are equal., If S1 = 0, S2 = 0 and S3 = 0 be any three given circles, then to obtain the radical centre, we solve any two of the, following S1 – S2 = 0 , S2 – S3 = 0 , S3 –S1 = 0, 67

Page 14 :
CIRCLE, ,  If  is the angle subtended at P(x1, y1) by the circle S = x + y + 2gx + 2fy + c = 0, then, 2, , , cot 2 , , 2, , S1, g2  f 2  c, ,  If the line lx + my + n = 0 is a tangent to the circle (x – h)2 + (y – k)2 = a2, then (hl + km + n)2 = a2 (l2 + m2).,  The length of the chord intercepted by the circle x2 + y2 = r2 on the line, ,  r 2 ( a 2  b 2 )  a 2b 2, 2 , , a2  b2, , , x y,   1 is, a b, , , , , , ,  The distance between the chord of contact of the tangents to the circle x2 + y2 + 2gx + 2fy + c = 0 from the, , 1 g2  f 2  c, origin and the point (g, f) is 2, ., g2  f 2, , , , a, , ,  The angle between the tangents from (, ) to the circle x + y = a is 2 tan , 2, 2, 2 , .,    a ,  If lines l1x + m1y + n1 = 0 and l2x + m2y + n2 = 0 cut the axes at concyclic points, then l1l2 = m1m2., 2, , 2, , 2, , –1, ,  The area of the triangle formed by the tangents from the points (h, k) to the circle x2 + y2 = a2 and their chord, of contact is, , a, 2, , h k, , 2, , (h 2  k 2  a 2 )3 / 2 ., ,  If O is the origin and OP, OQ are tangents to the circle x2 + y2 + 2gx + 2fy + c = 0, then the circumcentre of the, g f , ,, ., triangle OPQ is ,  2 2 , ,  If chord of a circle AB and CD meet at some point P, then PA . PB = PC . PD and if AB chord and tangent at, T meet at P, then PA . PB = PT2., T, , B, A, , P, , P, , A, C, , B, , D, ,  If OA and OB are the tangents from the origin to the circle x2 + y2 + 2gx + 2fy + c = 0 and C is the centre of the, circle then the area of the quadrilateral OABC is, , c( g2  f 2  c ) ., , 69

Page 15 :
CIRCLE, , SOLVED EXAMPLES, Ex.1, , Sol., , Ex.2, Sol., , The equation of the circle concentric with the circle x2 + y2 – 3x + 4y – c = 0 and passing through the point, (–1, –2) is, [1] x2 + y2 – 3x + 4y – 1 = 0, [2] x2 + y2 – 3x + 4y = 0, 2, 2, [3] x + y – 3x + 4y + 2 = 0, [4] none of these, The equation of two concentric circles differ only in constant term. So let the equation of the requird circle be, x2 + y2 – 3x + 4y +  = 0, It passes through (–1, –2) so we have, 1 + 4 + 3 – 8 +  = 0   = 0,, Hence required equation is x2 + y2 – 3x + 4y = 0, Ans.[2], If the line x + y = 1 is a tangent to a circle with centre (2, 3), then its equation will be, [1] x2 + y2 – 4x – 6y + 4 = 0, [2] x2 + y2 – 4x – 6y + 5 = 0, [3] x2 + y2 – 4x – 6y – 5 = 0, [4] none of these, Radius of the circle, , 4, = perpendicular distance of (2, 3) from x + y = 1 is, , 2, , 2 2, ,  the required equation will be, (x – 2)2 + (y – 3)2 = 8  x2 + y2 – 4x – 6y + 5 = 0, Ex.3, Sol., , If the lines 3x – 4y + 4 = 0 and 6x – 8y – 7 = 0 are tangents to a circle, then the radius of the circle is, (1) 3/2, (2) 3/4, (3) 1/10, (4) 1/20, The diameter of the circle is perpendicular distance between the parallel lines (tangents) 3x – 4y + 4 = 0, 7, and 3x – 4y –, = 0 and so it is equal to2, 4, 7/2, 3, , , 9  16, 9  16 2, Hence radius is, , Ex.4, Sol., Ex.5, Sol., , Ans.[2], , 3, ., 4, , Ans. [2], , The straight line (x – 2) + (y + 3) = 0 cuts the circle (x – 2)2 + (y – 3)2 = 11 at, (1) No points, (2) One point, (3) Two points, (4) None of these, Equation of line is x + y + 1 = 0. Since the perpendicular distance from centre to line is greaterr than radius,, hence it does not cut the circle., Ans. [1], The equation of the circle through the point of intersection of x2 + y2 – 1 = 0, x2 + y2 – 2x – 4y + 1 = 0 and touching, the line x + 2y = 0, is[1] x2 + y2 + x + 2y = 0 [2] x2 + y2 – x + 20 = 0 [3] x2 + y2 – x – 2y = 0, [4] 2(x2 + y2) – x – 2y = 0, Family of circles is, x2 + y2 – 2x – 4y + 1 + (x2 + y2 – 1) = 0, (1 + ) x2 + (1 + ) y2 – 2x – 4y + (1 – ) = 0, x2 + y2 , , 1 , 4, 2, y, x, 0, 1 , 1 , 1 , , 2 ,  1, ,, Centre is , 1, , , 1, ,  , , 2, , 2, , 1 , 4  2,  2 ,  1 , ,  ,  , ., and radius = , 1 , 1 ,  1  ,  1  , Since it touches the line x + 2y = 0, hence, Radius = Perpendicular from centre to the line., 2, 1, 2, 2, 1   4  , 1 , , i.e.,, 1 , 5  4  2, 12  22, ,  =±1, 70

Page 16 :
CIRCLE, , Ex.6, ,  = –1 cannot be possible in case of circle. So  = 1., Thus, we get the equation of circle., Ans.[3], If the straight line ax + by = 2; a, b  0 touches the circle x2 + y2 – 2x = 3 and is normal to the circle, x2 + y2 – 4y = 6, then the values of a and b are respectively, [1] 1, –1, , Sol., , [3] , , [2] 1, 2, , 4, ,1, 3, , [4] 2, 1, , Given x2 + y2 – 2x = 3,  centre is (1, 0) and radius is 2, and x2 + y2 – 4y = 6,  centre is (0, 2) and radius is, , , a(1)  b(0)  2, a2  b2, , 2, , 10 . Since line ax + by = 2 touches the first circle, , or (a – 2) = [2 a 2  b 2 ], , ...(i), , Also the given line is normal to the second circle. Hence it will pass through the centre of the second circle.,  a(0) + b(2) = 2 or 2b = 2 or b = 1, Putting this value in equation (i) we get, a – 2 = 2 a 2  12, , or (a – 2)2 = 4(a2 + 1), , or a2 + 4 – 4a = 4a2 + 4 or 3a2 + 4a = 0, , or, , a (3a + 4) = 0 or a = 0, , , 4, 3, ,  4 ,  values of a and b are   , 1 respectively according to the given choices.,  3 , , Ex.7, , Sol., , Ans.[3], , If the centre of a circle which passing through the points of intersection of the circle x2 + y2 – 6c + 2y + 4 = 0 and, x2 + y2 + 2x – 4y – 6 = 0 is on the line y = x, then the equation of the cirlce is, (1) 7x2 + 7y2 – 10x + 10y – 11 = 0, (2) 7x2 + 7y2 + 10x – 10y – 12 = 0, 2, 2, (3) 7x + 7y – 10x – 10y – 12 = 0, (4) 7x2 + 7y2 – 10x – 12 = 0, Family of circles through points of intersection of two circles is S1 + S2 (  –1)., x2 + y2 – 6x + 2y + 4 + (x2 + y2 + 2x – 4y – 6) = 0, Centre is (3 – , –1 + 2). It lies on y = x., 4, 3, Hence equation of circle can be found by substituting  in the family of circles above. Ans. [3], , Therefore, –1 + 2 = 3 –    =, , Ex.8, , A chord AB drawn from the point A(0, 3) at cirlce x2 + 4x + (y – 3)2 = 0 and it meets to M in such a way that, AM = 2AB, then the locus of point M will be, Y, (1) Straight line, (2) Circle, (3) Parabola, (4) none of these, 2, , Sol., , 2, , h, h k 3, ,  3  0,   4  , 2, 2, 2,  ,   , , , (-2,3), , B, , h2 8h (k  3)2, , ,  0 or x2 + y2 + 8x – 6y + 9 = 0, , 4, 4, 4, This is a circle., Ans. [2], , Ex.9, , (0, 3), A, , M, X', , 0, , The line 3x – 2y = k meets the circle x2 + y2 = 4r2 at only one point, if k2, (1) 20r2, , (2) 52r2, , (3), , 52 2, r, 9, , (4), , 20 2, r, 9, , 71

Page 17 :
CIRCLE, , Sol., , Equation of line is, 3x – 2y = k, Circle is x2 + y2 = 4r2, , ...(i), ...(ii), , Equation of line can be written as y =, , 3, k, x, 2, 2, , Here, c = –, , k, 3, ,m , 2, 2, , Now the line will meet the circle, if c = a 1  m 2, , Ex.10, , Sol., , =, , k, 3,  (2r ) 1   , 2, 2, , , , k2, 13,  4r 2 , 4, 4, , 2, , [from (ii), a = 2r], ,  k2 = 52r2., , Ans. [2], , The equation of the circle which passes through the intersection of x 2 + y2 + 13x – 3y = 0 and, 2x2 + 2y2 + 4x – 7y – 25 = 0 and whose centre lies on 13x + 30y = 0, (1) x2 + y2 + 30x – 13y – 25 = 0, (2) 4x2 + 4y2 + 30x – 13y – 25 = 0, 2, 2, (3) 2x + 2y + 30x – 13y – 25 = 0, (4) x2 + y2 + 30x – 13y + 25 = 0, The equation of required circles is s1 + s2 = 0,  25, 7, 0,  x2(1 + ) + y2(1 + ) +x(2 + 13) – y   3  ,  2, 2,   ( 2  13 ) 7 / 2  3 , ,, , Centre = , 2, 2, , , , , , Ex.11, , Sol., , Centre line on 13x + 30 y = 0, ,  7 / 2  3 ,  2  13 , 0,   30 ,  –13 , 2 , 2, , , , ,  =1, , Ans. [2], , Locus of a point which moves such that sum of the square of its distances from the sides of a square of side, unity is 9 is, (1) Straight line, (2) Circle, (3) Parabola, (4) none of these, x2 + (x – 1)2 + y2 + (y – 1)2 = 9, Ans. [2], , 72

Page 21 :
CIRCLE, , Q.37, , Centre of circle passing through the points (4, 5), (3, 4) and (5, 2) is, 9 7, [1]  , , 2 2, , Q.38, , Q.40, , 7 7, [3]  , , 2 2, , 9 9, [4]  , , 2 2, , The radius of the circle x2 + y2 + 2x cos  + 2y sin  = 8 is, [1] 1, , Q.39, , 7 9, [2]  , , 2 2, , [2] 3, , [3] 2 3, , [4], , 10, , The parametric cordinates of a point on the circle x2 + y2 – 2x + 2y – 2 = 0 are, [1] (1 + 2 cos , 1 + 2 sin ), , [2] (1 – 2 cos , 1 – 2 sin ), , [3] (1 + 2 cos , –1 + 2 sin ), , [4] (–1 + 2 cos , 1 + 2 sin ), , The equation of the circle whose centre is the origin and which passes through the vertices of an equilateral, triangle the length of whose median is 3a is, [1] x2 + y2 = a2, , Q.41, , Q.42, , [3] x2 + y2 = 4a2, , The equation of the circumcircle of the triangle by the lines x = 0, y = 0,, , [4] x2 + y2 = 9a2, x y,   1 isa b, , [1] x2 + y2 + ax – by = 0, , [2] x2 + y2 – ax + by = 0, , [3] x2 + y2 – ax – by – 0, , [4] x2 + y2 + ax + by = 0, , The point (1, 2) lies inside the circle x2 + y2 – 4x – 2y + c = 0, then, [1] c < 3, , Q.43, , [2] a2 + y2 = 16a2, , [2] c > 3, , [3] 2 < c < 3, , [4] none of these, , The equation of the circle passing through the vertices of the quadrilateral whose sides are x = 1, x = 2, y = 1 and, y = 2 is-, , Q.44, , [1] x2 + y2 – 3x – 3y + 2 = 0, , [2] x2 + y2 + 3x + 3y + 2 = 0, , [3] x2 + y2 – 3x – 3y + 4 = 0, , [4] none of these, , The value of c for which x + y = 2 touches circle x2 + y2 – 2cx = 0 and (1, 0) lies inside the circle, is[1] 2, , Q.45, , [2] 40, –10, , [3] 40, 10, , [4] –40, –10, , [2], , 3 y  x  10, , [3] y  3x  2, , [4] none of these, , The equation of tangent at the point on the circle x2 + y2 – 4x – 2y – 20 = 0, nearest from the point P(10, 7) is[1] 3x – 4y = 5, , Q.48, , [4] 2( 2  1), , The equation of the tangent to the circle x2 + y2 = 25 which is inclined at 60° angle with x-axis, will be, [1] y  3 x  10, , Q.47, , [3] 2( 2  1), , If the line 3x + 4y = m touches the circle x2 + y2 = 10x, then m is equal to[1] –40, 10, , Q.46, , [2] ( 2  1), , [2] 4x + 3y – 36 = 0, , [3] 4x + 3y + 14 = 0, , [4] none of these, , Area of circle in which a chord of length 2 3 subtends angle 120° at it’s centre is[1]  sq. units, , [2] 2 sq. units, , [3] 4 sq. units, , [4] none of these, , 76

Page 22 :
CIRCLE, , Q.49, , 2, , 2, , If y = 2x is a chord of the circle x + y = 10x, then the eauation of the circle whose diamter is this chord is[1] x2 + y2 + 2x + 4y = 0 [2] x2 + y2 + 2x – 4y = 0 [3] x2 + y2 – 2x – 4y = 0 [4] none of these, , Q.50, , The equation of common tangent of circles x2 + y2 = 4 and x2 + y2 – 8x + 12 = 0 at the point where they touch is[1] x = –2, , Q.51, , [2] y = 2, , [3] x = 2, , [4] y = –2, , The equation of chord of contact of circle x2 + y2 – 8x + 6y + 9 = 0 for the point (8, 1) is, [1] x + y + 5 = 0, , [2] x + y = 5, , [3] x – y + 5 = 0, , [4] x + y = 7, , Q.52, , The pole of the line lx + my + n = 0 with respect to the circle x2 + y2 = a2 is, , Q.53, ,   la2 ma 2 ,  la 2 ma 2 ,   la 2  ma 2 ,  la2  ma 2 , , , , , , , , , [1]  n , n , [2]  n , n , [4]  n , n , [3]  n , n , , , , , , , , , From the origin, chords are drawn to the circle (x – 1)2 + y2 = 1, then equation of locus of middle points of these, chords, is[1] x2 + y2 = 1, , Q.54, , [2] x2 + y2 = x, , [3] x2 + y2 = y, , [4] none of these, , If the circle x2 + y2 + 4x + 22y + c = 0 bisects the circumference of the circle x2 + y2 – 2x + 8y – d = 0, then, c + d is equal to[1] 60, , Q.55, , [3] 40, , [4] 56, , If the circles of same radius ‘r’ and centres at (3, 4) and (7, 8) cut orthogonally, then ‘r’ is equal to[1] 2, , Q.56, , [2] 50, , [2] 3, , [3] 4, , [4] 5, , Locus of the point of intersection of lines, x cos  + y sin  = a and x sin  – y cos  = a(  R) is, [1] x2 + y2 = a2, , Q.57, , [2] x2 + y2 = 2a2, , [3] x2 + y2 + 2x + 2y = a2 [4] none of these, , AB is diameter of a circle and C is any point on the circumference of the circle. Then, [1] the area of ABC is maximum, when it is isosceles., [2] the area of ABC is minimum, when it is isosceles., [3] the perimeter of ABC is minimum, when it is isosceles., [4] none of these, , Q.58, , The number of common tangent to the circles, x2 + y2 – 2x – 4y + 1 = 0, [1] 1, , Q.59, , and x2 + y2 – 12x – 16y + 91 = 0 is[2] 2, , [3] 3, , [4] 4, , The two circles x2 + y2 – 2x – 4y = 0 and x2 + y2 – 8y – 4 = 0, [1] intersect each other, , [2] touch each other internally, , [3] touch each other externally, , [4] none of these, 77

Page 23 :
CIRCLE, , Q.60, , If the circles x2 + y2 + 2x – 8y + 8 = 0 and x2 + y2 + 10x – 2y + 22 = 0 touch each other then, their point of contact, is -, ,  17 11 , (1)   ,, ,  5 5, Q.61, , Q.62, ,  17 11 , (3)  ,, ,  5 5, ,  11 , ,2 , (4)  ,  3 , , If a circle S1 bisects the circumference of another circle S2, then their radical axis, [1] passes through the centre of S1, , [2] passes through the centre of S2, , [3] bisects the line joining their centres, , [4] none of these, , The locus of a point such that tangents drawn from it to the circle x2 + y2 = a2 are at 120° is[1] 4x2 + 4y2 = 3a2, , Q.63, ,  11 , ,2 , (2) ,  3 , , [2] 3x2 + 3y2 = 4a2, , [3] x2 + y2 =, , 2a 2, 3, , [4] none of these, , Let A be the centre of the circle x2 + y2 – 2x – 4y – 20 = 0, and B(1, 7) and D(4 – 2) are points on the circle then,, if tangents be drawn at B and D, which meet at C, then area of quadrilateral ABCD is[1] 150, , Q.64, , [2] 75, , [3] 75/2, , [4] none, , The radical axis of two circles and the line joining their centres are, (1) Parallel, , (2) Perperdicular, , (3) Neither parallel, nor perpendicualr, , (4) Intersecting, but not fully perpendicular, , 78

Page 24 :
CIRCLE, , EXERCISE # 2, Q.1, , The tangents to x2 + y2 = a2 having inclinations  and  intersect at P. If cot  + cot  = 0, then locus of P is, [1] x – y = 0, , Q.2, , Q.3, , [2] x + y = 0, , [3] xy = 0, , [4] None of these, , The circle x2 + y2 + 2gx + 2fy + c = 0 bisects the circumference of the circle x2 + y2 + 2ax + 2by + d = 0, then, [1] 2a (g – a) + 2b (f – b) = c – d, , [2] 2a (g + a) + 2b (f + b) = c + d, , [3] 2g (g – a) + 2f (f – b) = d – c, , [4] 2g (g + a) + 2f (f + b) = c + d, , Three equal circles each of radius r touch one another. The radius of the circle touching all the three given circles, internally is, , [1] (2 +, , Q.4, , 3)r, , [2], , (2  3 ), 3, , r, , [3], , (2  3 ), 3, , r, , [4] (2 –, , 3)r, , If from any point P on the circle x 2 + y2 + 2gx + 2fy + c = 0, tangents are drawn to the circle, x2 + y2 + 2gx + 2fy + c sin2 + (g2 + f2) cos2 = 0, then the angle between the tangents is, [1] , , Q.5, , [2] 2, , [3] /2, , [4] none of these, , The possible values of P for which the line x cos  + y sin  = p is a tangent to the circle, x2 + y2 – 2qx cos  – 2qy sin  = 0 is/are, [1] q and 2q, , Q.6, , [2] 0 and q, , [3] 0 and 2q, , [4] q, , A square is inscribed in the circle x2 + y2 – 2x + 4y – 93 = 0 with its sides parallel to the coordinate axes. The, coordinates of its vertices are, , Q.7, , [1] (– 6, 9), (– 6, – 5), (8, – 9), (8, 5), , [2] (– 6, – 9), (– 6, 5), (8, – 9), (8, – 5), , [3] (– 6, – 9), (– 6, 5), (8, 9), (8, 5), , [4] (– 6, – 9), (– 6, 5), (8, 5), (8, – 9), , If the circle C1 : x2 + y2 = 16 intersects another circle C2 of radius 5 in such a manner that the common chord is, of maximum length and has a slope equal to 3/4, then the coordinates of the centre of C2 are, [1] (–9/5, – 12/5), , Q.8, , [2] (9/5, 12/5), , [3] (± 9/5,  12/5), , [4] none of these, , The locus of the point which moves so that the lengths of the tangents from it to two given concentric circles, x2 + y2 = a2 and x2 + y2 = b2 are inversely as their radii has equation, , Q.9, , [1] x2 + y2 = (a + b)2, , [2] x2 + y2 = a2 + b2, , [3] (a2 + b2)(x2 + y2) = 1, , [4] x2 + y2 = a2 – b2, , The equation of the circle which passes through (1, 0) and (0, 1) and has its radius as small as possible, is, [1] 2x2 + 2y2 – 3x – 3y + 1 = 0, , [2] x2 + y2 – x – y = 0, , [3] x2 + y2 – 2x – 2y + 1 = 0, , [4] x2 + y2 – 3x – 3y + 2 = 0, 79

Page 25 :
CIRCLE, , Q.10, , If a line passing through the point (–, , 8,, , 8 ) and making an angle 135º with x-axis cuts the circle, , x = 5 cos, y = 5 sin at points A and B, then length of the chord AB is, [1] 10, , Q.11, , [2] 5, , [3] 20, , [4] 2 5, , A line meets the coordinate axes in A and B. A circle is circumscribed about the triangle OAB. If m and n are the, distances of the tangent to the circle at the origin from the points A and B respectively, the diameter of the circle, is, [1] n(m + n), , Q.12, , [2] m + n, , [3] m (m + n), , [4], , 1, (m + n), 2, , The distance between the chords of contact of the tangents to the circle x2 + y2 + 2gx + 2fy + c = 0 from the, origin and from the point (g, f) is, , 2, , [1] g + f, Q.13, , 2, , 1 2 2, (g + f + c), [2], 2, , 2, 2, 1 g f c, [3], g2  f 2, 2, , 2, 2, 1 g f c, [4], 2, g2  f 2, , If a line segment AM = a, moves in the plane XOY remaining parallel to OX so that the left end point A slides along, the circle x2 + y2 = a2, the locus of M is, [1] x2 + y2 = 4a2, , Q.14, , [2] x2 + y2 = 2ax, , [3] x2 + y2 = 2ay, , [4] x2 + y2 – 2ax – 2ay = 0, , Given the circles x2 + y2 – 4x – 5 = 0 and x2 + y2 + 6x – 2y + 6 = 0. Let P be a point (, ) such that the tangents, from P to both the circles are equal. Then, [1] 2  + 10 + 11 = 0, , Q.15, , 2 a, , [2], , 3, a, 2, , [3], , 3a, , [4] None of these, , [2] 2, , [3] 3, , [4] 4, , If r = 2a cos represents a circle, then its centre is, [1] (0, – a), , Q.18, , [4] 10 + 2 + 11 = 0, , The number of common tangents to the circles x2 + y2 = 4 and x2 + y2 – 8x + 12 = 0 is, [1] 1, , Q.17, , [3] 10 – 2 + 11 = 0, , If an equilateral triangle is inscribed in the circle x2 + y2 = a2, the length of its such side is, , [1], , Q.16, , [2] 2 – 10 + 11 = 0, , [2] (a, a), , [3] (– a, 0), , [4] (a, 0), , If a line L  x cos60º + y sin60º + 1 = 0, cuts the circle S  x2 + y2 – a2 = 0 in the points A and B and equation, of circle with AB as diameter is S + L = 0, then  equals, [1] 2, , [2] 1, , [3] – 2, , [4] – 1, , 80

Page 26 :
CIRCLE, , Q.19, , Two equal circles of radius are intersect such that each passes through the centre of the other. The length of their, common chord is, [1], , Q.20, , 2r, , [2] 2r, , [2] ( 2 , 2 ), , 3 r/2, , [3] ( 2 , 2 2 ), , [4] none of these, , [2] (–4, –5) and (2, 3), , [3] (–4, –5) and (6, 7), , [4] none of these, , If a circle centred at (4, 3) touches a line x + y = 1, then it’s point of contact is, [1] (1, 2), , Q.23, , [4], , Centre of circles of radius 5 touching the line 3x + 4y = 7 at (1, 1) is[1] (4, 5) and (–2, –3), , Q.22, , 3r, , The image of the centre of the circle x2 + y2 = a2 with respect to the mirror x + y = 1 is-, , ,  1, , 2 , [1] , ,  2, Q.21, , [3], , [2] (1, 0), , [3] (0, 1), , [4] (0, 2), 2, , 2, , The abscissa of two points A and B are the roots of the euqation x + 2ax – b = 0 and their ordinates are the, roots of the equation y2 + 2py – q2 = 0. The radius of the circle with AB as a diameter will be[1], , Q.24, , Q.25, , a 2  b 2  p 2  q2, , b 2  q2, , [3], , a 2  b 2  p 2  q2, , [4], , a2  p2, , The equation of the circle on the common chord of circle (x – a)2 + y2 = a2 and x2 + (y + b)2 = b2 as diameter is[1] x2 + y2 = bx + ay, , [2] x2 + y2 = 2ab (bx + ay), , [3] (a2 + b2) (x2 + y2) = 2ab(bx – ay), , [4] (a2 + b2) (x2 + y2) = 2(bx + ay), , The locus of centres of all the circles passing through (1, 2) and cutting x2 + y2 = 16 orthogonally is[1] 4x – 2y + 21 = 0, , Q.26, , [2], , [2] x + 2y + 11 = 0, , [3] 2x + 4y – 21 = 0, , [4] 2x – y + 11 = 0, 2, , 2, , If the squares of the lengths of the tangents from a point P to the circles x + y =a2, x2 + y2=b2 and x2 + y2 = c2, are in A.P. then, [1] a,b,c are in GP, , Q.27, , [3] a2, b2, c2 are in AP, , [4] a2, b2, c2 are in GP, , The radical centre of the three circles x2 + y2 = a2, (x – c)2 + y2 = a2 and x2 + (y – b)2 = a2 isa b, [1]  , , 2 2, , Q.28, , [2] a, b, c are in AP, , b c , [2]  , , 2 2, , c b, [3]  , , 2 2, , [4] none of these, , Two vertices of an equilateral triangle are (–1, 0) and (1, 0) and its third vertex lies above the x-axis then its, circumcircle is2, , , 1 , 4, 2,  , [1] x   y , , 3, 3, , , 2, , , 1 , 4, 2,  , [2] x   y , , 3, 3, , , 2, , , 1 , 4, 2,  , [3] x   y , , 3, 3, , , , [4] none of these, , 81

Page 28 :
CIRCLE, , Q.11, , Q.12, , 2, , [1] 2x2 + 2y2 – 5x + y – 14 = 0, , [2] 7x – 3y + 18 = 0, , [3] 5x – y + 14 = 0, , [4] none of these, , [2] x + 10y + 2 = 0, , [3] x + 10y = 8, , [RPET-2001], , [4] x + 10y + 8 = 0, , If line x + 2y = 1 is the polar of circle x2 + y2 = 5 then pole is[2] (5, 5), , [RPET-2001], , [3] (–5, 10), , [4] (–5, –10), , Equation of tangent to the circle x2 + y2 = a2 which is parallel to y = mx + c[1] my = x ± a, , Q.15, , 2, , Radical axis of the circles 3x2 + 3y2 – 7x + 8y + 11 = 0 and x2 + y2 – 3x – 4y + 5 = 0 is-, , [1] (5, 10), Q.14, , 2, , The equation of radical axis of the circle x + y + x – y + 2 = 0 and 3x + 3y – 4x – 12 = 0 will be-[RPET-2000], , [1] x + 10y = 2, Q.13, , 2, , 1 m 2, , [2] y = mx ±, , 1 m 2, , [3] y = mx ± a 1 m 2, , [RPET-2001], [4] none of these, , The point from which the tangents to the circles x 2 + y2 – 8x + 40 = 0, 5x 2 + 5y2 – 25 x + 80 = 0,, x2 + y2 – 8x + 16y + 160 = 0 are equal in length is 15 , , [1]  8,,  2 , , Q.16, , 15 , , , [2]   8,, 2 , , , [RPET-2002],   15 , , [3]  8,, 2 , , , [4] none of these, , A variable chord is drawn through the origin to the circle x2 + y2 – 2ax = 0. The locus of the centre of the circle, drawn on this chord as diameter is[1] x2 + y2 + ax = 0, , Q.17, , [RPET-2002], , [2] x2 + y2 – ax = 0, , [3] x2 + y2 + ay = 0, , [4] x2 + y2 – ay = 0, , If line x + 2y = 5 is tangent to the circle x2 + y2 = 5 then equation of normal at their point of contact is[RPET-2003], [1] 2x + y = 0, , Q.18, , [2] 4x + 5y = 16, , [3] 5x – y = 5, , [RPET-2003], [4] none of these, , [2] a + b = 0, , [3] a = b & c = 0, , [RPET-2003], [4] g = f = 0, , Parametric coordinate of a curve is x = 3 + 2(cos2t – sin2t) & y = 4 + 4 sin t cos t) then curve is- [RPET-2003], [1] straight line, , Q.21, , [4] none of these, , Equation ax2 + 2hxy + by2 + 2gx + 2fy + c = 0 represents a circle if[1] a = b  0 & h = 0, , Q.20, , [3] x + 2y = 0, , Equation of radical axis of two circles x2 + y2 = 16 & (x – 4)2 + (y – 5)2 = 25 is[1] 3x + 5y = 8, , Q.19, , [2] 2x – y = 0, , [2] circle, , [3] parabola, , [4] none of these, , If the chord y = mx + 1 of the circle x2 + y2 = 1 subtends an angle of measure 45° at the major segment of the, circle then value of m is[1] 2, , Q.22, , [AIEEE-2002], [2] –2, , [3] 1, , [4] none of these, 2, , 2, , The centre of a set of circles, each of radius 3, lie on the circle x + y = 25. The locus of any point in the set is[AIEEE-2002], [1] 4  x + y  64, 2, , Q.23, , 2, , [2] x + y  25, 2, , 2, , [3] x + y  25, 2, , 2, , [4] 3  x + y  9, 2, , 2, , The centre of the circle passing through (0, 0) and (1, 0) and touching the circle x2 + y2 = 9 is[AIEEE-2002, IIT 91],  1 1, [1]  , , 2 2, , , 1, [2]  ,  2 , , 2, , 3 1, [3]  , , 2 2, , 1 3, [4]  , , 2 2, , 83

Page 30 :
CIRCLE, , Q.35, , 2, , 2, , 2, , 2, , 2, , Given that two circles x + y = r and x + y – 10x + 16 = 0, the value of r such that they intersect in real and, distinct point is given by[1] 2 < r < 8, , Q.36, , [IIT-94], [2] r = 2 or r = 8, , [3] r < 2 or r < 8, , [4] none of these, , A circle is inscribed in an equilateral triangle of side a, the area of any square inscribed in the circle is-[IIT-94], , a2, 2a 2, a2, a2, [2], [3], [4], 3, 3, 6, 12, The distance from the centre of the circle x2 + y2 = 2x to the straight line passing through the points of intersection, of two circles. x2 + y2 + 5x – 8y + 1 = 0 and x2 + y2 – 3x + 7y – 25 = 0 is[IIT-95], , [1], Q.37, , [1] 1, Q.38, , [2] 3, , [3] 2, , [4] 1/3, , The angle between a pair of tangents from a point P to the circle x2 + y2 + 4x – 6y + 9 sin2  + 13 cos2  = 0 is, 2. The equation of the locus of P is-, , Q.39, , [1] x2 + y2 + 4x – 6y + 4 = 0, , [2] x2 + y2 + 4x – 6y – 9 = 0, , [3] x2 + y2 + 4x – 6y – 4 = 0, , [4] x2 + y2 + 4x – 6y + 9 = 0, , The number of common tangents to the circles x2 + y2 = 4 and x2 + y2 – 6x – 8y = 24 is[1] 0, , Q.40, , [IIT-96], , [2] 1, , [3] 3, , [IIT-98], , [4] 4, , Let L1 be a straight line passing through the origin and L2 be the straight line x + y = 1. If the intercepts made by, the circle x2+y2–x+3y=0 on L1 & L2 are equal, then which of the following equation came represent L1 [IIT-99], [1] x + y = 0, , Q.41, , [2] x – y = 0, , [3] x – 7y = 0, , [4] none of these, , If two distinct chords drawn from the point (p, q) on the circle x2 + y2 = px + qy (where pq  0) are bisected by the, x-axis then-, , [IIT-99], , [1] p2 = q2, Q.42, , [2] p2 = 8q2, , [3] p2 < 8q2, , [4] p2 > 8q2, , The triangle PQR is inscribed in the circle x2 + y2 = 25. If Q and R have co-ordinates (3, 4) and (–4, 3) respectively,, then angle OPR is equal to[1] /2, , Q.43, , [2] /3, , [3] /4, , [4] /6, , If the circles x2 + y2 + 2x + 2ky + 6 = 0 and x2 + y2 + 2ky + k = 0 intersect orthogonally, then k is- [IIT-2000], [1] 2 or –3/2, , Q.44, , [IIT-2000], , [2] –2 or –3/2, , [3] 2 or 3/2, , [4] –2 or 3/2, , Let AB be a chord of the circle x2 + y2 = r2 subtending a right angle at the centre. Then the locus of the centroid, of the triangle PAB as P moves on the circle is[1] a parabola, , Q.45, , [2] a circle, , [IIT-2001], [3] an ellipse, , Let PQ and RS be tangent at the extremities of the diameter PR of a circle of radius r. If PS and RQ intersect at, a point X on the circumference of the circle, then 2r equals2PQ . RS, PQ  RS, [1] PQ . RS, [3], [2], PQ  RS, 2, , Q.46, , [4] a pair of straight lines, , If a > 2b > 0 then the positive value of m for which y = mx – b, , 1 m 2, , [IIT-2001], 2, , PQ  RS, 2, is a common tangent to x2 + y2 = b2 and, [4], , (x – a)2 + y2 = b2 is-, , [IIT-2002], , 2b, [1], , 2, , a  4b, , 2, , 2, , 2, , [2], , a  4b, 2b, , 2, , [3], , 2b, a  2b, , [4], , b, a  2b, , 85

Page 31 :
CIRCLE, , Q.47, , 2, , 2, , If the tangent at the point P on the circle x + y + 6x + 6y = 2 meets the straight line 5x – 2y + 6 = 0 at a point, Q on the y-axis, then the length of PQ is[1] 4, , Q.48, , [2] 2 5, , [3] 5, , [4] 3, , The centre of the circle inscribed in the square formed by lines x2–8x+12=0 & y2 – 14y + 45 = 0, is-[IIT-2003], [1] (4, 7), , Q.49, , [IIT-2002], , [2] (7, 4), , [3] (9, 4), , [4] (4, 9), , A diameter of the circle x2 + y2 – 2x – 6y + 6 = 0 is a chord of another circle C with centre (2, 1). The radius of this, circle C is[1] 1, , Q.50, , [2] 3, , Q.52, , Q.54, , [3] 12 , , [2] 6  4 3, , 7 3, 4, , [4] 3 , , 7 3, 4, , [2] {(x, y) : x2 + (y – 1)2 = 4}  {(x, y) : y  0}, , [3] {(x, y) : x2 = y}  {(0, y) : y  0}, , [4] {(x, y) : x2 = 4y}  {(0, y) : y  0}, , Tangent to the curve y = x2 + 6 at a point P(1, 7) touches the circle x2 + y2 + 16x + 12y + c = 0 at a point Q. Then, the coordinates of Q are, [IIT 2005], [2] (–9, –13), , [3] (–10, –15), , [4] (–6, –7), , If the lines 3x – 4y – 7 = 0 and 2x – 3y – 5 = 0 are two diameters of a circle of area 49  square units, the equation, of the circle is, [AIEEE- 2006], [1] x2 + y2 + 2x – 2y – 62 = 0, , [2] x2 + y2 – 2x + 2y – 62 = 0, , [3] x2 + y2 – 2x + 2y – 47 = 0, , [4] x2 + y2 + 2x – 2y – 47 = 0, , Let C be the circle with centre (0, 0) and radius 3 units. The equation of the locus of the mid points of the chords, of the circle C that subtend an angle of 2/3 at its centre is, [AIEEE- 2006], [2] x2 + y2 =, , 27, 4, , [3] x2 + y2 =, , 9, 4, , [4] x2 + y2 =, , 3, 2, , Consider a family of circles which are passing through the point (–1, 1) and are tangent to x-axis. If (h, k) are the, co-ordinates of the centre of the circles, then the set of values of k is given by the interval, [AIEEE- 2007], [1], , Q.56, , 3, , [1] {(x, y) : x2 = 4y}  {(x, y) : y  0}, , [1] x2 + y2 = 1, Q.55, , [4], , A circle is given by x2 + (y – 1)2 = 1, another circle C touches it externally and also the x-axis, then the locus of, its centre is, [IIT 2005], , [1] (–6, –11), Q.53, , [3] 2, , In an equilateral triangle 3 coins of radii 1 unit each are kept so that they touch each other and also the sides of, the triangle. Area of the triangle is, [IIT 2005], [1] 4  2 3, , Q.51, , [IIT-2004], , , , 1, 1, k, 2, 2, , [2], , k, , 1, 2, , Column-I, , [3], , 0k, , 1, 2, , [4], , k, , 1, 2, , Column-II, , A. Two intersecting circles, , p. Have a common tangent, , B. Two mutually external circles, , q. Have a common normal, , C. Two circles one strictly inside the other, , r. Do not have a common tangent, , D. Two branches of a hyperbola, , s. Do not have a common normal, , Correct match of statements in column I with properties in column II is :, [1] (A, p), (B, q), (C, r), (D, s), , [2] (A, p), (B, p), (C, q and r), (D, q and r), , [3] (A, q), (B, p), (C, s), (D, r), , [4] (A, p), (B, s), (C, s), (D, r), , [IIT-JEE- 2007], , 86

Page 32 :
CIRCLE, , Q.57, , Consider L1 : 2x + 3y + p – 3 = 0, L2 : 2x + 3y + p + 3 = 0, where p is a real number and, C : x2 + y2 + 6x – 10y + 30 = 0, , [IIT-JEE- 2008], , Statement -I : If line L1 is chord of circle C, then line L2 is not always a diameter of circle C., and, Statement -II : If line L1 is a diameter of circle C, then line L2 is not a chord of circle C., Correct answer is :, [1] Statement I is true, statement II is true and II is a correct explanation for I., [2] Statement I is true, statement II is true but II is not a correct explanation for I., [3] Statement I is true, statement II is false., [4] Statement I is false, statement II is true., Q.58, , Let a and b be non-zero real numbers. Then the equation (ax2 + by2 + c) (x2 – 5xy + 6y2) = 0 represents :, [IIT-JEE- 2008], [1] Four straight lines, when c = 0 and a, b are of the same sign, [2] Two straight lines and a circle, when a = b and c is of sign opposite to that of a, [3] Two straight lines and a hyperbola, when a and b are of the same sign and c is of sign opposite to that of a, [4] A circle and an ellipse, when a and b are of the same sign and c is of sign opposite to that of a, Passage :- A circle C of radius 1 is inscribed in an equilateral triangle PQR. The point of contact of C with side, , PQ, QR and RP are D, E, and F respectively. If PQ is, , 3 3 3, , , , and, D, is, 3xy6,  2 2  and origin and centre of, , , , the circle lies on same side of PQ, then :, Q.59, , In equation of circle C is :, 2, , Q.60, , [1] ( x  2 3 ) 2  ( y  1) 2  1, , 1, , 2, [2] ( x  2 3 )   y    1, 2, , , [3] ( x  3 ) 2  y  12  1, , [4] ( x  3 ) 2  y  12  1, , Equations of the sides QR and RP are :, [1] y , , 2, , [3] y , , 3, 3, x 1, x  1, y  , 2, 2, , 3, , x  1, y  , , 2, 3, , x 1, , [IIT-JEE- 2008], [2] y , , 1, 3, , xy0, , [4] y  3 x , y  0, , 87

Page 33 :
CIRCLE, , Q.61, , In points E and F are given by :, ,  3 3, , , [1]  2 , 2 , ( 3 ,0), , , Q.62, , Q.64, , 3 3   3 1, , , , [4]  2 , 2 ,  2 , 2 , , , , , [2] (–3, –4), , [3] (3, 4), , [4] (3, –4), , Tangents are drawn from the point P(1, 8) to the circle x2 + y2 – 6x – 4y – 11 = 0 which touch the circle at points, A and B. The equation of the circumcircle of the triangle PAB is :, [IIT-JEE- 2009], [1] x2 + y2 + 4x – 6y + 19 = 0, , [2] x2 + y2 – 4x – 10y + 19 = 0, , [3] x2 + y2 – 2x + 6y – 29 = 0, , [4] x2 + y2 – 6x – 4y + 19 = 0, , The centres of two circles C1 and C2 each of unit radius are at a distance of 6 units from each other. Let P be the, midpoint of the line segment joining the centres of C1 and C2 and C be a circle touching circles C1 and C2, externally. If a common tangent to C1 and C passes through P is also a common tangents to C2 and C, then the, radius of the circle C is :, [1] 4, , Q.65, ,  3 3  3 1, , , , [3]  2 , 2 ,  2 , 2 , , , , , The point diametrically opposite to the point P(1, 0) on the circle x2 + y2 + 2x + 4y – 3 = 0 is : [AIEEE- 2008], [1] (–3, 4), , Q.63, ,  3 1, , , [2]  2 , 2 , ( 3 ,0), , , , [IIT-JEE- 2008], , [2] 8, , [3] 5, , [4] 6, , If P and Q are the points of intersection of the circles x2 + y2 + 3x + 7y + 2p – 5 = 0 and, x2 + y2 + 2x + 2y – p2 = 0, then there is a circle passing through P, Q and (1, 1) for :, , Q.66, , [1] All except one value of p, , [2] All except two values of p, , [3] Exactly one value of p, , [4] All values of p, , The circle x2 + y2 = 4x + 8y + 5 intersects the line 3x – 4y = m at two distinct points if :, [1] 35 < m < 85, , Q.67, , [2] – 85 < m < – 35, , [3] – 35 < m < 15, , [2] |a| = c, , [3] a = 2c, , [AIEEE- 2010], , [4] 15 < m < 65, , The two circles x2 + y2 = ax and x2 + y2 = c2(c > 0) touch each other if :, [1] 2|a| = c, , Q.68, , [AIEEE- 2009], , [AIEEE- 2011], [4] |a| = 2c, , The circle passing through the point (–1, 0) and touching the y-axis at (0, 2) also passes through the point :, [IIT-JEE- 2011],  3 , [1]   ,0 ,  2 , , Q.69, ,  5 , [2]   ,2 ,  2 , ,  3 5, [3]   , ,  2 2, , [4]  4,0 , , The length of the diameter of the circle which touches the x – axis at the point (1, 0) and passes through the, point (2, 3) is :, (1), , 10, 3, , [AIEEE – 2012], (2), , 3, 5, , Passage, , (3), , 6, 5, , (4), , 5, 3, , [IIT – 2012], , A tangent PT is drawn to the circle x 2  y 2  4 at the point P( 3 , 1) . A straight line L, perpendicular to PT is a, tangent to the circle ( x  3) 2  y 2  1 :, , 88

Page 34 :
CIRCLE, , Q.70 A possible equation of L is :, (A) x  3 y  1, , (B) x  3 y  1, , (C) x  3 y  1, , (D) x  3 y  5, , (C) x  3 y  4, , (D) x  2 2 y  6, , Ans :- A, Q.71 A common tangent of the two circles is :, (A) x = 4, , (B) x = 2, , Ans :- D, Q.72, , The circle passing through (1, –2) and touching the axis of x at (3, 0) also passes through the point :, [JEE Mains – 2013], (1) (5, –2), , Q.73, , (2) (–2, 5), , (3) (–5, 2), , (4) (2, –5), , Let C be the circle with centre at (1, 1) and radius = 1. If T is the circle centred at (0, y), passing through origin, and touching the circle C externally, then the radius is T is equal to :, , [JEE Mains – 2014], , 3, , 1, 1, 3, (3), (4), (2), 2, 4, 2, 2, The locus of the mid – point of the chord of contact of tangents drawn from points lying on the straight line, , (1), Q.74, , 4 x  5y  20 to the circle x 2  y 2  9 is :, , [IIT – 2012], , (1) 20( x 2  y 2 )  36 x  45 y  0, , (2) 20( x 2  y 2 )  36 x  45 y  0, , (3) 36( x 2  y 2 )  20 x  45 y  0, , (4) 36( x 2  y 2 )  20 x  45 y  0, , ANSWER KEY, EXERCISE - 1, Que . 1, Ans. 3, Que . 26, Ans. 2, Que . 51, Ans. 2, , 2, 1, 27, 4, , 3, 3, 28, 3, , 4, 1, 29, 1, , 5, 3, 30, 2, , 6, 3, 31, 3, , 7, 2, 32, 4, , 8, 1, 33, 1, , 9, 2, 34, 4, , 10, 4, 35, 3, , 11, 2, 36, 3, , 12, 1, 37, 1, , 13, 1, 38, 2, , 14, 2, 39, 3, , 52, 3, , 53, 2, , 54, 2, , 55, 3, , 56, 2, , 57, 1, , 58, 4, , 59, 2, , 60, 1, , 61, 2, , 62, 2, , 63, 2, , 64, 2, , 15, 3, 40, 3, , 16, 4, 41, 2, , 17, 3, 42, 1, , 18, 3, 43, 3, , 19, 3, 44, 3, , 20, 4, 45, 2, , 21, 2, 46, 1, , 22, 2, 47, 2, , 23, 2, 48, 3, , 24, 4, 49, 3, , 25, 2, 50, 3, , EXERCISE - 2, Que. 1, 2, 3, 1, 2, Ans. 3, Que. 26 27 28, 3, 1, Ans. 3, , 4, 2, , 5, 3, , 6, 4, , 7, 3, , 8, 2, , 9, 2, , 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25, 1, 2, 4, 2, 3, 3, 3, 4, 1, 3, 4, 1, 2, 1, 3, 3, , EXERCISE - 3, , 89