Page 1 :
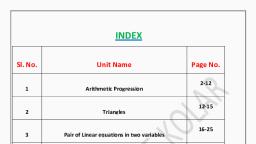
MINORITY MORARJI DESAI RESIDENTIAL SCHOOL BELAGAVI, TOWN SSLC MATHEMATICS PASSING PACKAGE 2021-22, (TARGET 40+), S. NO, , UNIT NAME, , 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, TOTAL, , PASSING, MARKS, ARITHMETIC PROGRESSIONS, 2+2, TRIANGLES, 4/5, PAIR OF LINEAR EQUATIONS IN TO 2+4, VARIABLES, CIRCLES, 3, CONSTRUCTIONS, 4+3+2, COORDINATE GEOMETRY, 2+2+1, QUADRATIC EQUATIONS, 2+2, INTRODUTION TO, 1, TRIGONOMETRY, STATISTICS, 3+3, SURFACE AREAS AND VOLUMES, 1, , TOTAL, MARKS, 4, 4, 6, 3, 9, 5, 4, 1, 6, 42, , 7, , CHAPTER 1. ARITHMETIC PROGRESSIONS:, Formulas:, , 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, , Answer the following questions:, 1) Find the term of an AP/ Find the common difference of an AP(1m), 1, If the nth term of an arithmetic progression is an=4n+5 then find, the 3rd term?, Ans: (n=3),, an=4n+5,, a3=4(3) +5, a3=12+5, a3=17., 2, If the nth term of an arithmetic progression is an=3n+2 then, find the 12th term?, 3, If the nth term of an arithmetic progression is an=5n-3 then find, the 5th term?, 4, If the nth term of an arithmetic progression is an=2n2+3 then, find the a2 term?, 5, In an AP if an = 3 + 4n then the value of a3 is?, 6, In an AP if an = 3 + 2n then find a4., , AP- An arithmetic progression is a list of numbers in which each, term is obtained by adding a fixed number to the proceeding term, except the first term., General form of AP is, a, a + d, a+2d, a+3d………a+ (n-1) d., n th term of AP is, an= a+(n-1) d., n th term from last of AP is = l-(n-1) d., Common difference of an AP is d=a2-a1, d= a3-a2, 𝐧, , Sum of the first n term of an AP is, Sn=𝟐 [𝟐𝐚 + (𝐧 − 𝟏)𝐝], Sum of the first n term of an AP first term and last term given is, 𝐧, 𝐧, Sn=𝟐 [a+ l]. Or Sn=𝟐 [a+ an], 𝐧(𝐧 𝟏), , Sum of the first nth +ve integers is Sn = 𝟐, In any progression Sn - Sn-1 = an, If a. b, c are in AP then the arithmetic mean between a and c is, 𝐚 𝐜, b= 𝟐, , In an AP If an=3n-1 then the common difference of the given, progression is?, Ans: Put n=1,2,3,, an=3n-1,, a1=3(1)-1=3-1=2,, a2=3(2)-1=6-1=5,, d=a2-a1=5-2=3., 8, The nth term of an AP is 7-4n. Find the common difference., 9, In an AP If an=3n-1 then the common difference of the given, progression is?, 10, What is the common difference of an AP in a18-a14 =32?, Ans: a18-a14 =32,, a+17d-(a+13d) =32,, a+17d-a-13d=32,, 4d=32, d=32/4,, d=8, MMDRS BELAGAVI. NAGAPPA. KUMBAR, 1
Page 2 :
11, , If the common difference of an AP is 5, then what is value of, a18- a13?, Ans: d =5,, a18 -a13 = a+17d-(a+12d), =a+17d-a-12d, =17d-12d, =17(5)-12(5), =85-60=15., 12, If the common difference of an arithmetic progression is 3, then find, the value of 𝑎7 − 𝑎2., Ans: 𝑎7 − 𝑎2 = 𝑎 + 6𝑑 − (𝑎 + 𝑑), 𝑎 + 6𝑑 − 𝑎 – 𝑑, = 5𝑑 = 5(3) = 15, ∴ 𝑎7 − 𝑎2. = 15, , If 2, x,14 are in arithmetic progression, then the value of x is?, 2, x, 14 ., a1, a2, a3 (common difference is d), d=a2-a1, d= a3-a2, a2-a1= a3-a2,, x-2=14-x,, 2x=14+2,x=16/2,, x=8, 14, If 8, x – 1, 16 are in Arithmetic Progression, then find the value of x., 15, If - 3, a, 2 are the three consecutive terms of an AP then find a., 2) Find the nth term of the following A.P, 16, Using formula find the 10th term of A.P in 2, 7, 12,………., Ans: 2, 7, 12,……….AP ,a = 2 and d = a2 -a1 = 7 - 2 = 5, a10 =?, , 21, 22, 23, 24, 25, 26, 27, 28, , 3) Find the sum of first n terms of arithmetic progression:, 29, Find the sum of 20 terms of arithmetic series 5+10+15+… using, suitable formula, Ans: 5 + 10 + 15 + ......., a1, a2, a3,, Sum of 20 terms S 20 =?, d =a2-a1= 5, Sn= [2a + (n − 1)d]., , 13, Ans:, , a1, a2, a3,, an = a + (n - 1) d, a10 = 2 + (10 -1)5, a10 = 2 + 9 × 5, a10 = 2 + 45, ∴ a10 = 47., , 17, 18, 19, 20, , Find the 25th term of an arithmetic progression 2,6,10, 14…, In an AP 21, 18, 15,…..find 35th term, , In an AP 3 ,8, 13 ……find 10th term., Find the 25th term of A.P in 5, 10, 15, 20,….., , Find the 10th term of A.P in 5, 8, 11,………., Find the 15th term of A.P in 12, 19,26,………, Find the 25th term of A.P in 7, 13,10,…, Find the 15th term of A.P in 5,8,11,14,………, Find the 22th term of A.P in 8,3,- 2,………., Find the 20th term of A.P in 4, 7, 10,………., In an AP 10, 7, 4, ………find 30th term, In an AP - 3, - , 2, ………find 11th term, , n = 20, a = 5,, , S20= [2(5)(20 − 1)5]., S 20 = 10 [10 + (19) 5], S 20 = 10 [10 + 95], S 20 = 10 x 105, S 20 = 1050., , 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, , Find the sum of 2+5+8……to 20 terms using formula., Find the sum of first 20 terms of the arithmetic progression 3,8,13,…, using formula, Find the sum of the AP 2, 7, 12, …upto 10 terms., Find the sum of the AP 2, 7, 12, …up to 15 terms., Find the sum of first twenty terms of arithmetic series 2+7+12+…, using suitable formula., Find the sum of first 20 terms of the series 4 + 7 + 10 + ......, Find the sum of 5+8+11+…… to 10terms using the formula., Find the sum of first 15 terms of the arithmetic progression, 12, 19, 26,………using formula., Find the sum of first 15 terms of the arithmetic progression, 5, 8,11,14…….…using formula, Find the sum of the AP 8, 3, -2,.. upto 22 terms, Find the sum of the AP - 37, -33, -29,….upto 12 terms. using formula, Find the sum of first 30 terms of the arithmetic progression, 10, 7, 4,……...…, 2
Page 3 :
4.Find the nth term from the last of the following A.P, 42, In an AP 10, 7, 4, ……………-62 find 11th term from last., Ans: 10, 7, 4, ……………-62, , a1, a2, a3,………………………an, d = a2 - a1 = 7 -10 = -3 and an= l = - 62,, 11th term from last =?, nth term of an AP from last = l - (n - 1) d, n=11, 11th term of this AP from last = - 62 - (11 - 1) (-3), 11th term of this AP from last = - 62 - (10) (-3), 11th term of this AP from last = - 62 + 30, 11 th term of this AP from last = - 32., In an AP 3, 8, 13, ……253 find 20th term from last., In an AP 21, 18, 15, …… —81 find 28th term from last., , 42, 43, 4) Find the number of terms(n) of the following A.P, 44, Ans:, , 45, 46, 47, 48, 49, , Which term of the AP 21, 18, 15, ………… is - 81?, 21, 18, 15, …………-81 Here a = 21 and d = a2 - a1 = 18 - 21 = - 3,, a1, a2, a3,……………………… an ,, an = - 81, n =?, an = a + (n - 1) d, - 81 = 21 + (n -1)(-3), - 81 = 21 - 3n + 3, 3n = 24 + 81, 3n = 105, n = 35,, 35th term of the given AP is -81, Which term of the AP 3, 8, 13, ………… is 78?, Which term of the AP 7, 13, 19,…………is 205?, Check whether 301 is a term of the list of numbers 5, 11, 17, 23, . . ., Check whether − 150 is a term of the A.P. 11, 8, 5, 2, …, , 53, , If a1 , a2 , a3 , a4 , …. are in arithmetic progression, then the common, difference is, (A) 𝑎2 − 𝑎1 (B) 𝑎1 − 𝑎2, (C) 𝑎2 − 𝑎3, (D) 𝑎3 − 𝑎4, , 54, , The common difference of the arithmetic progression, 3, 7, 11, 15, …., . is, (A) -4 (B) 3 (C) 4 (D) 5, 55 An arithmetic progression among the following is, (A) 3, 5, 7, 10, . .(B) 3,5,6,9, . .(C) -2,-1, 0, 3, . . (D) 4, 7, 10, 13, . ., 56 The sum of the first 30 odd natural numbers is, (A) 300, (B) 600, (C) 150 (D) 900, 57, , Write the formula to find the sum of first ‘n’ terms of an, arithmetic progression with the first term‘a’ and the last term an., (A) Sn= [a- an] (B) Sn= [a+ an] (C) Sn= [2a+ an] (D) Sn=, [a+2a], , Check whether 130 is a term of the A.P. 3,7,11, …, , 50 The nth term of an arithmetic progression with first term ‘a’ and, , common difference ‘d’, is, (A) an=a+(n-1)d (B) an=a-(n-1) C) an=a-(n+1)d, (D) an=a+(n+1)d, 51 In an arithmetic progression, if the first term is ‘a’ and the common, difference is ‘d’ , then thesum of its first ‘n’ terms is, (A)Sn= [2a + (n − 1)d], (B) Sn= [2a − (n − 1)d], , (C) Sn= [2a + (n + 1)d], , (D) Sn= [a + (n − 1)d], MMDRS BELAGAVI TOWN -NAGAPPA. KUMBAR., 3
Page 6 :
1) Solve the given pair of linear equations by elimination method:, (solve x and y), 1, Solve the given pair of linear equations by elimination method, x + y = 14 and x — y = 4, Ans: x + y=14 …….(1) , x-y=4………(2), (1)+(2), x + y=14, x - y=4, =======, 2x=18, x=9 put x=9 in (1), 9+y=14, y=14-9, y=5 , x=9,y=5, 2, 2x+y=3,4x-y=9, 11, x + y=10, x – y = 2, 3, x + y= 9, x - y= 1, 12, x + y=14, x-y=2, 4, x-y=2, 2x-y=8, 13, 2x+y=6, 2x-y=2, 5, 3x+y=15, 2x-y=5, 14, 2x - y=2, 4x - y= 4, 6, 2x+y=11, x + y=8, 15, 3x-y=-4, 5x+y=-4, 7, x + y=8, 2x-y=7, 16, x + y=5,2x - 3y=5, 8, x + y=5, 2x-3y=4, 17, y-x+2=0, x-2y-4=0, 9, 3x+4y=10, 2x-2y=2, 18, x+2y=5, 2x-3y=-4, 10, 2x+3y=11, 2x-4y=-24, 19, 3x+2y=1 and 2x-3y=3, 2) Solve the following pair of linear equations by Graphically:, 1, 2, 3, 4, , 5, 6, 7, 8, 9, 10, , x + y=5, x-y=1, x + y=5, 2x-y=4, 2x+y=8, x-y=1, x + y=7, 3x-y=1, 2x-y=2, 4x-y=4, 2x+y=8, x + y=5, y=2x-2, y=4x-4, 2x + y=5, x + y=4, x+3y=6, 2x-3y=12, 2x+y=6, 2x-y=2, , 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, , 1) Solve Graphically: x + y=5, x-y=1, x + y=5, , x 0 1 2 3, y 5 4 3 2, , x-y=1, , x, y, , 0 1 2 3, -1 0 1 2, , 2x+y-6=0,2x-y-2=0, x=y-6, y=2-x, x-y=4, 2x+y=5, x + y=5, 2x-y=4, 2x+y=4,2x-y=4, x +y=6,, 3x-y=10, 2X +y=8, x+2y=1, x-2y=0, 3x+4y-20=0, x+2y-4=0, 2x+4y-12=0,, 2x+3y-9=0, 4x+6y-18=0, , 11 2x+y=10, x +y=6, , MMDRS BELAGAVI TOWN -NAGAPPA. KUMBAR., 6
Page 7 :
Chapter-4. Circles:, Theorem -1., Prove that “The length of tangents drawn from an external point to, a circle are equal”, Data: O is centre of circle., P is external point., PQ & PR are tangents, To Prove: PQ=PR, Construction: Join OP, OQ &OR., Proof: in ΔOPQ and ΔOPR, OQ=OR (radii of the same circle), OP=OP (common side), ∟Q=∟R=900 (radius ⊥ to tangents), ΔOPQ ≅ ΔOPR (RHS Postulate), PQ=PR. (CPCT), Theorem -2., Prove that “The tangent at any point of a circle is perpendicular to, the Radius through the point of contact”., Data: O is the centre of circle., XY is tangent., P is point of contact., R, OP is a radius of circle., To Prove: OP ⊥ XY, Construction: make a point Q on XY, join OP & OQ., OQ intersect the circle at point R., Proof: compare OQ &OR. Q is outside the circle., OP = OR (radius of the same circle), OQ > OR (construction), OQ > OP, OP ⊥ XY., , Chapter- 5. Constructions:, 1) Divide the line segment in the given ratio:, 1, Draw a line segment of length 7.6cm and divide in the ratio 5:8., Ans: 5:8. (5+8=13), 7.6cm, , 2, 3, 4, 5, 6, 7, 8, , Draw a line segment of AB=8cm and divide it in the ratio 3:2 by, geometrical construction., Draw a line segment of length 6 cm and divide it in the ratio 2: 3., Draw a line segment of length 9 cm and divide it in the ratio 1: 2., Draw a line segment of length 6 cm and divide it in the ratio 2: 3., Draw a line segment of length 9 cm and divide it in the ratio 3: 5., , Draw a line segment of length 6.5 cm and divide it in the ratio 3:4, Draw a line segment of length 9.5 cm and divide it in the ratio 3:2, , OP is least distance to XY., , 1 A line that intersects a circle at two distinct points is called a secant., 2 A line that intersects a circle at only one point is called tangent., 3 Maximum number of tangents draws to a circle from an external point:, 2 tangents, 4 A circle can have infinitely many parallel tangents at the most., , MMDRS BELAGAVI TOWN -NAGAPPA. KUMBAR., 7
Page 8 :
2) To construct a pair of tangents to a circle from an external point, from way from the centre, 9, Draw a circle of radius 5cm construct a pair of tangents to it from a, point 10cm away from its center. Measure their lengths, Ans:, , 14, , Draw a circle of radius 3.5 cm from a point 4 cm away from the, circle. construct the pair of tangents to the circle, 15, Draw a circle of radius 4cm from a point 5 cm away from the circle., construct the pair of tangents to the circle., 4) To construct a tangent to a circle from any point on the, Circumference of the circle, 16, Draw a circle of radius 4cm and construct a tangent at a point ‘P’ on, the circle., Ans:, , 5, , Length of tangents AP=BP=8.7cm, Draw a circle of radius 4cm constructs a pair of tangents to it from a, point 8cm away from its center., 11, Draw a circle of radius 4.5cm constructs a pair of tangents to it from, a point 8cm away from its center., 12, Draw a circle of radius 3.5cm construct a pair of tangents to it from a, point 8.5cm away from its center. Measure their lengths., 3) To construct a pair of tangents to a circle from an external point, from way from the circle:, 13, Draw a circle of radius 3cm from a point 5cm away from the circle., construct the pair of tangents to the circle. Measure their lengths, Ans:, 10, , 17, 18, , Draw a circle of radius 3cm and construct a tangent at a point ‘P’ on, the circle., Draw a chord length 3 cm in a circle of radius 2.5cm construct, tangents at the end of the chord., , Length of tangents AP=BP=7.4cm, 8
Page 9 :
19, 20, 21, Ans:, , Draw a chord length 6 cm in a circle of radius 4 cm construct, tangents at the end of the chord., Draw a chord AB of length 5 cm in a circle of radius 3 cm. Construct, a tangent at the point B., Draw a tangents to the ends of the diameter radius of circle is 4cm, , 5) To construct tangents to a circle when angle between the tangents, is given., 26, Draw a pair of tangents of a circle of radius 5cm which are inclined, to each other at an angle of 600. Measure the lengths of tangents., Ans: 1800-600=1200, , Length of tangent=PB=PA=8.7cm, Draw a pair of tangents of a circle of radius 4cm which are inclined, to each other at an angle of 600. Measure the lengths of tangents., 28, Draw a circle of radius 3.5 cm. Construct a pair of tangents to it such, that the angle between them is 60°., 29, Draw a pair of tangents of a circle of radius 4 cm such that the angle, between the tangents is 700. Measure the lengths of tangents, 30, Draw a circle of radius 3 cm. Construct two tangents to it, such that angle between them is 50°., 31, Draw a circle of radius 3 cm. Construct a pair of tangents to it such, that the angle between them is 60°., 6) To construct tangents to a circle when angle between the radii is, given., 32, Draw a pair of tangents of a circle of radius 4 cm such that the, angle between the radius is1200, Ans:, 27, , 22, 23, , Draw a tangents to the ends of the diameter radius of circle is 3.5cm, Draw a tangent to the one ends of the diameter, diameter of circle is, 5.8cm, , Ans:, , 24, , Draw a circle of radius 3 cm and construct a tangent at one end, of its diameter., , 9
Page 10 :
33, , Draw a pair of tangents of a circle of radius 4 cm such that the, angle between the radius is1200, , 34, , Draw a pair of tangents of a circle of radius 4 cm such that the angle, between the radius is 800., Draw a pair of tangents of a circle of radius 3.5 cm such that the angle, between the radius is 1100, Draw a pair of tangents of a circle of diameter 5 cm such that the angle, between the radius is1200, , 35, 36, , 39, , Draw a circle of radius 3cm take two points P and Q on one of its extended, diameters each at a distance of 7cm from its Centre draw tangents to the, circle from these two points P and Q., , Ans:, , 7) construct the tangents to the circle:, Draw two concentric circles of radii 2 cm and 4cm from a point 7cm away, 37, from its Centre construct the tangents to the circle., , Ans:, 40, , Draw a line segment AB of length 8cm. taking A as center, draw a circle of, radius 4cm and taking B as center draw the other circle 3cm. construct, tangents to each circle from the center of the other circle., , Ans:, , 38, , Construct a tangent to a circle of radius 3cm from a point on the circle of, radius 5cm and measure its length., , Ans:, , 38, , 8) Similar triangle constructions:, 41, Construct a triangle with sides 5cm, 6cm and 7cm, then a triangle, similar to it whose sides are 3/4 of the corresponding sides of the, first triangle., Ans:, 6cm, 5cm, Length of tangent AP=BP=4.6cm, Construct a tangent to a circle of radius 4cm from a point on the circle of, radius 6cm and measure its length., , 7cm, , 10
Page 11 :
42, 43, 44, 45, , Construct the triangle with sides are 5cm, 6cm, and 7cm and then, construct another triangle whose sides are 2/3 of the corresponding, side of the given triangle., Construct the triangle with sides 5cm, 6cm and 7cm and then, construct another triangle whose sides are in the ratio 3/5 of the, corresponding side of the given triangle, Construct the triangle ABC of its sides BC=3.5cm, AB= 5cm and, AC=4.5cm then construct a triangle similar to is whose sides are 5/7, of the corresponding side of the given triangle ABC., Construct a triangle of sides 4cm, 5cm and6cm and then a triangle, similar to it whose sides are 7/5of the corresponding sides of, the first triangle, , 48, 49, , Construct the triangle ABC with side base BC=8cm, and altitude, 4cm and then construct another triangle whose sides are in the ratio, 5/3 times the corresponding side of the isosceles triangle ABC., Construct the triangle ABC with sides BC=6cm, AB=5cm, and, ∟ABC=600 then construct another triangle whose sides are in the, ratio 3/4 of the corresponding side of the given triangle., , Ans:, , Ans:, 5cm, , 6cm, 50, 7cm, 51, 52, , 46, 47, , Construct the triangle ABC with sides are AB=BC= 6cm ∟B= 500, and then construct another triangle whose sides are in the ratio 4/7, of the corresponding side of the given triangle., Draw a right triangle in which the sides (other than Hypotenuse) are, of the length 4cm and 3cm construct another triangle whose sides, are in the ratio 5/3 of the corresponding side of the given triangle., Construct the triangle ABC with sides are BC=7cm, ∟B= 450 and,, ∟A= 1050 then construct another triangle whose sides are in the, ratio 4/3 of the corresponding side of the given triangle., , Construct the triangle ABC of its sides BC=4 cm, AB= 6cm and, AC=4.5cm then construct a triangle similar to is whose sides are 4/3, of the corresponding side of the given triangle ABC., Construct the isosceles triangle whose base is 8cm, and altitude 4cm, and then construct another triangle whose sides are in the ratio, 1, the corresponding side of the isosceles triangle ABC., , Ans:, , MMDRS BELAGAVI TOWN -NAGAPPA. KUMBAR., 11
Page 12 :
=196-154=42 cm2, , CHAPTER-6. AREA RELATED TO CIRCLES:, Formula:, 5, , ABCD is a square of side 14 cm. Four congruent circles are drawn, in the square as shown in the figure. Calculate the area of the, shaded region. Circles touch each other externally and also sides of, the square., , Ans: (r = 7/2 cm), , area of the shaded region=area of square, – 4X area of circle, , =(14)2-4X πr2, =196-154, =42cm2, 6, , 1, , Length of an arc of sector of angle 𝜃 =, , 𝑋2πr., , Length of an arc of a sector of a circle of radius r and angle is?, Write the formula to find area of a sector of a circle, if angle at the, centre is ‘’ degrees.?, Find the area of the sector of a circle with radius 4 cm and of angle, 3, 45°. (Use = 3·14)., Ans: r=4cm, 45°., , In the figure, ABCD is a square of side 14 cm. A, B, C and D are the, centres of four congruent circles such that each circle touches, externally two of the remaining three circles. Find the area of the, shaded region, r=7cm, Ans:, Area of the shaded region=area of the square – 4X area of quadrant, of circle. (ans:42 cm2), , 1, 2, , Area of sector =, , 𝑋 πr2 sq unit, , = 𝑋 π(4)2= 𝑋 πX4X4, =2π sq unit, In the figure, ABCD is a square, and two semicircles touch each, 4, other externally at P. The length of each semi-circular arc is equal, to 14 cm. Find the area of the shaded region., Ans: (r = 14/2=7cm), Area of square =(side)2=(14)2=196, Area of 2 semi circle = πr2=154, , 7, , In the adjoining figure each corner of a square of side 4 cm a, quadrant of a circle of radius 1 cm is cut and also a circle of, diameter 2 cm is cut as shown in figure. Find the area of the, remaining portion of the square., Area of the shaded region=area of the square – (4X area of quadrant of, circle+ area of circle), , Area of the shaded region=area of square – area of 2 semicircles, , 12
Page 13 :
Chapter -7. Coordinate geometry, Formulas:, Distance between the two points (X1, Y1) and (X2, Y2), 1, d= (𝐱𝟐 − 𝐱𝟏)𝟐 + (𝒚𝟐 − 𝒚𝟏)𝟐, Distance between the Origin and coordinates of a pints (x, y)., 2, d= 𝐱 𝟐 + 𝐲 𝟐, The coordinates of the midpoint of the line segment joining the, 3, 𝒙𝟏 𝒙𝟐 𝒚𝟏 𝒚𝟐, points (X1, Y1) and (X2, Y2), P (X, Y) = [, , 𝟐 ], 𝟐, The coordinates of the points P (x, y) which divides the line segment, 4, joining the points (X1, Y1) and (X2, Y2) internally in ratio m1:m2., 𝐦𝟏𝐗𝟐 𝐦𝟐𝐗𝟏, 𝐦𝟏𝐲𝟐 𝐦𝟐𝐲𝟏, P (x, y) = [ 𝐦𝟏 𝐦𝟐 ,, ], 𝐦𝟏 𝐦𝟐, Area of the triangle whose vertices are (x1, y1), (x2, y2) and (x3, y3)., 5, 𝟏, Area of ∆ = 𝟐 [x1(y2-y3) +x2(y3-y1) +x3(y1-y2)], 6, The coordinates of the origin (0,0), 1, 2, 3, 4, , The Coordinates of the origin is, A) (1,1), B) (0,0), C) (0,1), D) (1,0), The perpendicular distance of the point P (2, 3) from the x-axis is, A)1 unit, B) 2 units, C) 3 units, D)5 units, , The coordinates of a point P on the x-axis are of the form, A) (𝗑, 0), B) (0, 𝑦), D) (0, 𝑥), C) (𝑦, 0), , The distance between the co-ordinates of a point (p, q ) from the, origin is, a) d= 𝒑𝟐 + 𝒒𝟐 b) d= 𝒑𝟐 − 𝒒𝟐 c) d = 𝑝 + 𝑞 d) d=p2+q2, Find the distance of point, The distance of the coordinates point P (4, 3) from x-axis is, 5, A)3 units B)4 units C)5 units D)7 units, The distance of the point P (3, 4) from y-axis is, 6, A)3 units B)4 units C)5 units D)7 units., Find the distance of point (+ 12, + 5), 7, a) from the x-axis b) from the y-axis., The distance between the origin:, The distance between the origin and the point (– 12, 5), 8, Ans: d= 𝐱 𝟐 + 𝐲 𝟐 = (−2)𝟐 + (5)𝟐 = √ 144 + 25 = √169=13 unit, , Find the distance of the point P (5, 12) from the origin., 9, Find the distance between origin and the point (– 8, 15)., 10, Find the distance between origin (6, -8), 11, Find the distance between origin. (4, -3), 12, Find the distance between origin. (5, -5), 13, Find the distance between origin A (-6,8) and B (0,0), 14, Distance between the two points (X1, Y1) and (X2, Y2), Find the distance between the points (2, 3) and (4,1)., 15, Ans: (2, 3) and (4,1)., (X1, Y1) and (X2, Y2), d= (𝐱𝟐 − 𝐱𝟏)𝟐 + (𝒚𝟐 − 𝒚𝟏)𝟐, d= (4 − 2)𝟐 + (1 − 3)𝟐, d= (2)𝟐 + (−2)𝟐, d= √ 4 + 4, d= √ 4X2, d= 2√ 2 unit, Find the distance the coordinate of the points A (2,3) and B (10, -3), 16, Find the distance between the points A (3,6) and B (5,7) using, 17, distance formula, Find the distance the coordinate of the points A (8,3) and B (2,11), 18, Find the distance the coordinate of the points A (8, -3) and B (0,9), 19, Find the distance the coordinate of the points A (-5, -7) and B (-1, 3), 20, Find the distance the coordinate of the points A (-6,8) and B (0,0), 21, Find the distance the coordinate of the points A (a, b) and B (-a, -b), 22, Find the values of y in which the distance between the points P (2, –, 23, 3) and Q (10, y) is 10 units, The distance between the points (3, 1) and (0, x) is 5 units. Find x., 24, Find the perimeter of the triangle whose vertices are (-2,1) (4,6) and, 25, (6,3), Show that the triangle whose vertices are A (8 , – 4) , B (9 ,5), 26, and C (0, 4) is an isosceles triangle., , MMDRS BELAGAVI TOWN -NAGAPPA. KUMBAR., 13
Page 14 :
The coordinates of the midpoint of the line segment joining the, points (X1, Y1) and (X2, Y2),, 𝒙𝟏 𝒙𝟐, , 𝒚𝟏 𝒚𝟐, , P (X, Y) = [, , 𝟐 ], 𝟐, Find the coordinates of the mid-point of the line segment joining, 27, the points (2, 3) and (4, 7), Ans: (2, 3) and (4, 7), (X1, Y1) and (X2, Y2), 𝒙𝟏 𝒙𝟐 𝒚𝟏 𝒚𝟐, P (X, Y) = [, , 𝟐 ], 𝟐, P (X, Y) = [, , The coordinates of the points P (x, y) which divides the line segment, joining the points (X1, Y1) and (X2, Y2) internally in ratio m1:m2, , 𝟐, , ,, , 𝟐, , P (x, y) = [, , 𝐦𝟏𝐗𝟐 𝐦𝟐𝐗𝟏, 𝐦𝟏 𝐦𝟐, , 𝐦𝟏𝐲𝟐 𝐦𝟐𝐲𝟏, , ,, , 𝐦𝟏 𝐦𝟐, , ], , 37, , Find the coordinates of the points which divides the line segment, joining the points (4, -3) and (8, 5) in the ratio 3:1., , Ans:, , (4, -3), and (8, 5) m1:m2=3:1., (X1, Y1) and (X2, Y2), 𝐦𝟏𝐗𝟐 𝐦𝟐𝐗𝟏, 𝐦𝟏𝐲𝟐 𝐦𝟐𝐲𝟏, P (x, y) = [ 𝐦𝟏 𝐦𝟐 ,, ], 𝐦𝟏 𝐦𝟐, , ], , P (X, Y) = [ 𝟐 , 𝟐 ], P (X, Y) = [ 3, 5 ], , P (x, y) = [, , 𝟑𝐗𝟖, , P (x, y) = [, P (x, y) = [ ,, P (x, y) = [7,3], , 𝐗𝟒, , ,, , 𝟒, , ,, , 𝟑𝐗𝟓, , (, , ), , ], , ], ], , 28, , Find the coordinates of the mid-point of the line segment joining, the points (6,2) and (4,4), , 29, , Find the coordinates of the mid-point of the line segment joining, the points (2,1) and (4,7), , 38, , Find the coordinates of the points which divides the line segment, joining the points (-1, 7) (4, -3) in the ratio 2:3., , 30, , Find the coordinates of the mid-point of the line segment joining, the points (-5,7) and (-1,3), , 39, , Find the coordinates of the points which divide the line segment, joining the points (1, 6) and (4, 3) in the ratio 1:2., , 31, , Find the coordinates of the mid-point of the line segment joining, the points (5, 6) and (– 3, 8), , 40, , Find the co-ordinates of the point P, which divides the line joining A, (0, 0) and B (5, 10) in the ratio of 2:3., , 32, , Find the coordinates of the mid-point of the line segment joining, the points (-5,7) and (-1,3), , 41, , 33, , Find the coordinates of the mid-point of the line segment joining, the points (4, -5) and (6,3), , Find the co-ordinates of the points of trisection of the line segment, joining, (4, -1) and (-2, -3)., , 42, , 34, , Find the coordinates of the mid-point of the line segment joining, the points(-3,10) and (6, -8), , Find the coordinates of the points which divide the line segment, joining A (-2,2) and B (2,8).in to four equal parts., , 43, , 35, , Find the coordinates of a point A where AB is the diameter of a, circle whose Centre is (2, – 3) and B (1, 4), , If A and B are (-2, -2) and (2, -4), respectively, find the coordinates, of P such that AP= AB and P lies on the line segment AB., , 36, , Find the radius of circle whose Centre is (-5,4) and which passes, through the point (-7,1), 14
Page 15 :
44, Ans, , In what ratio does the point (-4, 6) divided the line segment joining, the points A (-6, 10) and B (3, -8)?, P(x,y)=, ∴ P(x,y) = [, , 46, , 𝐦𝟏𝐗𝟐 𝐦𝟐𝐗𝟏, , ,, , 𝐦𝟏 𝐦𝟐, 𝟑𝐦𝟏 𝟔𝐦𝟐, 𝟖𝐦𝟏, , (-4,6) = [, , 45, , (−6, 10) 𝑎𝑛𝑑 (3, −8), (X1, Y1) and (X2, Y2), , (−4, 6), , ,, , 𝐦𝟏𝐲𝟐 𝐦𝟐𝐲𝟏, 𝐦𝟏 𝐦𝟐, 𝐦𝟐, , 𝐦𝟏 𝐦𝟐, 𝐦𝟏 𝐦𝟐, 𝟑𝐦𝟏 𝟔𝐦𝟐, , ], , ], , Consider, −4 =, −4𝑚1 − 4𝑚2 = 3𝑚1−6𝑚2, 2𝑚2 = 7𝑚1, =, ∴ 𝑚1: 𝑚2= 2 : 7, In what ratio does the point (-2, 3) divided the line segment joining, the points A (-3, 5) and B (4, -9)?, Find the ratio in which the line segment joining the points (-3, 10), and (6, -8) is divided by (-1, 6)., , Area of the triangle whose vertices are (x1, y1), (x2, y2) and (x3, y3)., 𝟏, Area of ∆ = 𝟐 [x1(y2-y3) +x2(y3-y1) +x3(y1-y2)], 47, , Ans:, , Find the area of the triangle whose vertices are (1, 2), (3, 7) and, (5, 3)., , 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, , Find the area of the triangle whose vertices are (1, -1) (-4,6) and, (-3, -5), Find the area of the triangle whose vertices are A (5,2), B (4,7) and, C (7, -4)., Find the area of the triangle whose vertices are A (2,3), B (-1,0) and, C (2, -4), Find the area of the triangle whose vertices are A (-5, -1) B (3, -5),, and C (5,2), Find the area of the triangle formed by the points P (-1.5, 3) and, Q (6, -2) and R (-3, 4), The points A (1, 1), B (3, 2) and C (5, 3) cannot be the vertices of the, triangle ABC. Justify, find the value of k if the points A (2,3), B (4, k) and C (6, -3) are, collinear. (area of ∆= 𝟎), find the value of k if the points (7, -2), (5,1), and (3, k) are collinear, find the value of k if the points (8,1), (k, -4), and (2, -5) are collinear, Find the value of ‘k’. If the co-ordinates of the points A (2, -2), B (4, 2) andC (-7, k) are collinear., Determine if the points (1,5), (2,3) and (-2, -11) are collinear., Find the area of the quadrilateral whose vertices, taken in order are, (-4, -2), (-3, -5), (3, -2) and (2,3)., , (1, 2), (3, 7) and (5, 3)., (x1, y1), (x2, y2) and (x3, y3)., 𝟏, Area of ∆ = 𝟐 [x1(y2-y3) +x2(y3-y1) +x3(y1-y2)], 𝟏, , Area of = 𝟐 [1(7 − 3) + 3(3 − 2) + 5(2 − 7)], 𝟏, , Area of = 𝟐 [1(4) + 3(1) + 5(−5)], Area of =, , 48, , 𝟏, 𝟐, 𝟏, , [4 + 3 − 25], , Area of = 𝟐 [−18] = −9, But Area cannot be negative, Area of given triangle is 9 square units, Find the area of the triangle whose vertices are A (10, -6) B (2,5) and, C (-1,3), 15
Page 16 :
Chapter-8. Quadratic equations:, 1, 2, , ax2+bx+c=0, , The standard form of a quadratic equation, (a≠0), Formula used to find the roots of a quadratic equation ax2+bx+c=0,, 𝒃± 𝒃𝟐 𝟒𝒂𝒄, , 3, 4, , 5, , 1, , 2, , 3, , 4, , 5, 6, 7, 8, 9, , 𝒙=, 𝟐𝒂, Discriminate of the quadratic equation is b2-4ac, Nature of the roots a quadratic equation ax2+bx+c= 0, a) Two distinct real roots, if b2-4ac > 0, b) Two equal real roots, if b2-4ac = 0 or b2=4ac, C) No Real roots, if b2-4ac < 0, 2, In quadratic equation ax +bx+c= 0 if b2-4ac = 0 then the roots of, equation are x=, , x=, The value of the discriminant of a quadratic equation is 3. Then the, nature of its roots is, A) Real and Distinct, B) Real and equal, C)There is no any root, D) Imaginary numbers, The value of the discriminant of a quadratic equation is 0, Then the, nature of its roots is, A) Real and Distinct, B) Real and equal, C)There is no any root, D) Imaginary numbers, The standard form of quadratic equation is, A) 𝑎𝑥2 - 𝑏𝑥 + 𝑐 = 0 B) 𝑎𝗑2 + 𝑏𝗑 + 𝑐 = 0, C) 𝑎𝑥2 - 𝑏𝑥 − 𝑐 = 0 D) 𝑎𝑥2 + 𝑏𝑥 − 𝑐 = 0, The quadratic equation whose roots are -1 and 2 is, A) 𝗑2 − 𝗑 − 2 = 0 B) 𝑥2 − 𝑥 + 2 = 0, C)𝑥2 + 𝑥 − 2 = 0, D) 𝑥2 + 𝑥 + 2 = 0, If the roots of the quadratic equation x2+6x+k=0 are equal, then the, value of k is A)9 B) -9 C) 8 D) 5., The discriminant of the quadratic equation ax2+bx+c=0 is, A) b2= ac. B) b2- 4ac. C) √𝑏 − 4𝑎𝑐 . D) b2+4ac., If one root of the equation (x+4) (x+3) = 0 is -4 then find another, root of the equation.?, If one root of the equation (x-2) (x-3) = 0 is 3 then find another root, of the equation?, The standard form of the quadratic equation x 2 = 3x + 5 is?, , 10, Find the discriminant of the quadraticequation 𝑥2 + 2𝑥 + 1 = 0, Ans:, 𝑏2 − 4𝑎𝑐 = 22 − 4(1)(1), =4−4, 2, ∴ 𝑏 − 4𝑎𝑐 = 0, 11, Write the discriminant of the quadraticequation 𝑎𝑥2 + 𝑏𝑥 + 𝑐 = 0?, 12, Find the roots of the quadratic equation, Ans: 𝑥2 − 25 = 0, 𝑥2 = 25, 𝑥 = √25, ∴ 𝑥 = ±5, Find the nature of roots:, 13, Find the nature of the roots of theequation, 𝑥 2 + 2𝑥 − 15 = 0, Ans: 𝑎 = 1,, 𝑏 = 2,, 𝑐 = −15, 2, 2, 𝑏 − 4𝑎𝑐 = (2) − 4(1) (−15), = 4 + 60, = 64, Here 𝑏2 − 4𝑎𝑐 > 0, ∴Roots are Real and Distinct, 14, Find the nature of the roots of theequation 4𝑥 2- 12𝑥 + 9 = 0, Ans: 𝑎 = 4,, 𝑏 = −12,, 𝑐=9, 𝑏2 − 4𝑎𝑐 = (−12)2 − 4(4)(9), = 144 − 144, 2, 𝑏 − 4𝑎𝑐 = 0, Roots are Real and Equal, 15, Find the nature of the roots of theequation 𝑥 2 − 𝑥 + 12 = 0, Ans: 𝑎 = 1,, 𝑏 = −1,, 𝑐 = 12, 2, 2, 𝑏 − 4𝑎𝑐 = (−1) − 4(1)(12), = 1 − 48, = −47, Here 𝑏2 − 4𝑎𝑐 < 0, ∴ The equation has no real roots., 16, What is the nature of the roots of the quadratic equation, ax 2 + bx + c = 0 if, i)b 2 – 4ac = 0 ii) b 2 – 4ac < 0 iii) b 2 – 4ac> 0, 16
Page 19 :
Chapter -10. Statistics:, 𝑓𝑜𝑟𝑚𝑢𝑙𝑎𝑠:, , 1, , 𝒖𝒑𝒑𝒆𝒓 𝒄𝒍𝒂𝒔𝒔 𝒍𝒊𝒎𝒊𝒕 𝒍𝒐𝒘𝒆𝒓 𝒄𝒍𝒂𝒔𝒔 𝒍𝒊𝒎𝒊𝒕, , 2, , Mid-point (Xi) =, 𝟐, F𝑜𝑟𝑚𝑢𝑙𝑎 𝑡𝑜 𝑓𝑖𝑛𝑑 𝑡ℎ𝑒 𝑚𝑒𝑎𝑛 𝑜𝑓 𝑔𝑟𝑜𝑢𝑝𝑒𝑑 𝑑𝑎𝑡𝑎 by direct method, 𝜮 𝒇𝒊𝒙𝒊, mean (Ẋ) = 𝜮 𝒇𝒊, , 3, , Find the mean of Ungrouped data mean (Ẋ) =, , 4, 5, , 𝜮 𝒙𝒊, 𝑵, , 𝒏, , Formula to find the median of grouped data Median =l+ ( 𝟐, , 𝒄𝒇, 𝒇, , )𝑿𝒉, , Formula to find the mode of grouped data, 𝒇𝟏 𝒇𝟎, Mode =l+ (, )𝑿𝒉, , 8, 9, 10, 11, 12, 13, 14, 15, 16, , 𝟐𝒇𝟏 𝒇𝟎 𝒇𝟐, , I-lower limit of the modal class, f o- frequency of the class preceding the modal class, f1 - frequency of the modal class, f2 - frequency of the class succeeding the modal class, h – class size., 6 Class size (h) =𝑢𝑝𝑝𝑒𝑟 𝑐𝑙𝑎𝑠𝑠 𝑙𝑖𝑚𝑖𝑡 − 𝑙𝑜𝑤𝑒𝑟 𝑐𝑙𝑎𝑠𝑠 𝑙𝑖𝑚𝑖t, 7 Empirical relationship between the tree measures of central tendency, 3 median = mode + 2 mean, mode= 3 median - 2 mean, 2mean= 3median – mode., 8 The three measures of central tendency are mean, median, mode., 9 Range = highest score – lowest score., 10 Mode: more repeated score., 11 Median: given score arrange in ascending or descending order middle, score is median., , 1, Find the mean of the following data 7,6,5,0,7,8,9?, Ans: mean (Ẋ) = 𝜮 𝒙𝒊 = 𝟕 𝟔 𝟓 𝟎 𝟕 𝟖 𝟗 = 𝟒𝟐 = 𝟔, 𝑵, 𝟕, 𝟕, 2, Find the mean of the following data 2, 4, 6, 8, 10.?, 3, The mean value of 10, 15, 5, 20 and 50 is, (A)10 (B) 5 (C) 15 (D) 20, 4, If the mean of 5 scores is 6, then the sum of all the scores is, A)11 B) 26 C)30 D) 42., 5, Find the median of the scores 5, 8,14,16,19 and 20?, Ans: 5, 8,14,16,19,20 median=, =15, 6, Calculate median for the given score 1, 5, 4, 3, 2?, 7, Find the median of the scores 2, 8, 10, 6, 12, 16, , The median of 7, 3, 6, 14, 13, 11, 19 is (A) 7 (B) 13 (C) 11 (D) 19, Find the median of 24, 31, 17, 29, 36, 39, Find the mode of the score 1,3,2,1,3,4,3,4,3,5,3?, Find the mode, if mean is 58 and median is 50?, The midpoint of the C-I 10-25?, Find the mid-point of the class-interval 5 – 15., What is other name of the cumulative frequency curve?, In the following which is not a measure of central tendency?, A) mode B) range C) mean D) median, The using empirical formula If mean is 29.75 and mode is 24.5, then the median of the data is, A)48 B)28, C)53, D)28.5, , Find the mean of the following data, by direct method., Find the arithmetic mean of the following frequency distribution, xi, 3, 4, 5, 7, 10, fi, 3, 4, 8, 5, 10, xi, fi, fiXxi, Ans, 𝜮 𝒇𝒊𝒙𝒊, 𝟐𝟎𝟎, 3, 3, 9, mean (Ẋ) =, =, :, 𝜮 𝒇𝒊, 𝟑𝟎, 17, , 4, 5, 7, 10, , 18, , 4, 8, 5, 10, ∑𝑓𝑖 = 30, , 16, 40, 35, 100, ∑𝑓𝑖 𝑋𝑥𝑖 = 200, , Find mean for the following frequency distribution, Class Interval, Frequency, , Ans, , = 𝟔. 𝟔𝟔, , 0-10 10-20, 3, 5, , Class, Interval, , Frequency, , 0-10, 10-20, 20-30, 30-40, 40-50, , 3, 5, 9, 5, 3, ∑𝑓𝑖, = 25, , Midpoint, (xi), 5, 15, 25, 35, 45, , 20-30, 9, , 30-40, 5, , 40-50, 3, , fiXxi, 15, 75, 225, 175, 135, ∑𝑓𝑖𝑋𝑥𝑖, = 625, , 𝜮 𝒇𝒊𝒙𝒊, , mean (Ẋ) = 𝜮 𝒇𝒊, 𝟔𝟐𝟓, =, 𝟐𝟓, mean (Ẋ) = 𝟐𝟓., , MMDRS BELAGAVI TOWN -NAGAPPA. KUMBAR., 19
Page 20 :
20.Find the Median of the following frequencydistribution., , 19 Find the mean of the following data, by direct method, Class, internal, 1-5, 5-9, 9-13, 13-17, 17-21, , Frequency, , Class, internal, 5-15, 15-25, 25-35, 35-45, 45-55, , 4, 3, 5, 7, 1, N=20, , 30-60, 60-90, , 6, 9, , 90-120, 120-150, , 6, 4, , 4, 3, 6, 5, 2, , Class, , Class, Frequency, interval, 0-30, 5, , C.I., 1-5, 6 -10, 11-15, 16-20, , Frequency, , Class Frequency, interval, 45-55, 3, 55-65, 10, 65-75, 11, 75-85, 8, 85-95, 3, N=35, , Frequency, , interval, 1-3, 3-5, 5-7, 7-9, 9-11, , f, 4, 3, 2, 1, n=10, , 7, 8, 2, 2, 1, N=20, , N=30, CI, 0-3, 3-6, 6-9, 9-12, 12-15, , C-I, f, , C-I, f, , Frequency, 15, 16, 3, 4, 2, N=40, 50-52, 15, , 15-25, 6, , 53-55, 110, , 25-35, 11, , 56-58, 135, , 35-45, 7, , 59-61, 115, , 45-55, 4, , 4, , 65-75, 2, , 75-85, 1, , 0-10, 4, , 10-20, , 20-30, , 30-40, , 40-50, , 7, , 13, , 9, , 3, , FrequencyCumulative N=36, =, Frequency, , Class, Interval, , = 18, l=20, cf=11, h=10,, , f=13,, , 0-10, 10-20, 20-30, 30-40, 40-50, , 4, 7, 13, 9, 3, N=36, , 4, 11, 24, 33, 36, , Median =l+ (, , )𝑋ℎ, , =20+ (, , )𝑋10, , =20+ (, , )𝑋10, , =20+ (, , )=20+5.38=25.38., , 21.Find the median for the following data in the frequency distribution, table:, C-I, f, , 1-4, 6, , C-I, f, , 15-20, 2, , 4-7, 30, , 7-10, 40, , 20-25, 3, , 10-13, 16, 25-30, 6, , 13-16, 4, 30-35, 4, , 16-19, 4, 35-40, 5, , C-I, , 0-20, , 20-40, , 40-60, , 60-80, , 80-100, , 100-120, , 120-140, , F, , 6, , 8, , 10, , 12, , 6, , 5, , 3, , C-I, , 135-140, , 140-145, , 145-150, , 150-155, , 155-160, , 160-165, , f, , 4, , 7, , 18, , 11, , 6, , 5, , Classinterval, , 62-64, 25, , 55-65, , Class interval, Frequency, , 1—4, , Frequency, (f ), i, 6, , 4—7, , 30, , 7 — 10, , 40, , 10 — 13, , 16, , Class- Frequency, interval, 20 — 40, , 7, , 40 — 60, , 15, 20, , 13 — 16, , 4, , 60 — 80, , 16 — 19, , 4, , 80 — 100, , 8, , MMDRS BELAGAVI TOWN -NAGAPPA. KUMBAR., 20
Page 21 :
22. Find the mode for the following data:, Class interval Frequency 𝒇𝟏 = 𝟏𝟏, 𝒇𝟎 = 𝟗, 𝒇𝟐 = 𝟔,h=10, l=60, 𝒇𝟏 𝒇𝟎, 30-40, 4, Mode =l+ ( 𝟐𝒇𝟏 𝒇𝟎 𝒇𝟐)𝑿𝒉, 40-50, 7, 𝟏𝟏 𝟗, Mode =60+ (, )𝑿𝟏𝟎, 50-60, 9, 𝟐𝑿𝟏𝟏 𝟗 𝟔, 𝟐, Mode =60+ ( 𝟐𝟐 𝟏𝟓)𝑿𝟏𝟎, 60-70, 11, 𝟐, 70-80, 6, Mode =60+ ( 𝟕)𝑿𝟏𝟎 =60+2.85=62.85., 80-90, 2, Classinterval, 0—5, 5 — 10, 10 —15, 15 —20, 20 —25, , classinterval, 1—3, 3—5, 5—7, 7—9, 9 — 11, , Frequency, (f ), i, 8, 9, 5, 3, 1, ⅀f i = 26, , Frequency, , Family size, Number of, families, , 6, 9, 15, 9, 1, , Classinterval, 10 — 25, 25 — 40, 40 — 55, 55 — 70, 70 — 85, 85 — 100, , Frequency, (f ), i, 2, 3, 7, 6, 6, 6, , Class-interval, 0 — 10, 10 —20, 20 —30, 30 —40, 40 —50, , 1-3, 7, , 3-5, 8, , 5-7, 2, , Class-interval, 0 — 10, 10 —20, 20 —30, 30 —40, 40 —50, , Frequency, (f ), i, 7, 9, 15, 11, 8, , 7-9, 2, , 9 - 11, 1, , Class, interval, 0-30, 30-60, 60-90, 90-120, 120-150, , Construct” less than type of ogive” for the following data:, 23.The marks scored by 30 Students of class X, in the Mathematics are, given below.Draw a less than type ogive., Marks, Number of students, , 0-20, 5, , 20-40, 3, , 40-60, 11, , 60-80, 2, , 80-100, 9, , Ans:, , Frequency, (f ), i, 6, 9, 15, 9, 1, ⅀f = 40=N, i, , Marks, , No of, students, , Less than 20, Less than 40, Less than 60, Less than 80, Less than 100, , 5, 3, 11, 2, 9, , Number Coordinats, of, (x,y), students, 5, (20,5), 8, (40,8), 19, (60,19), 21, (80,21), 30, (100,30), , Frequency, 5, 6, 9, 6, 4, N=30, , 24.Change the following distribution to a less than type distribution, and draw, its ogive., CI, 0-3, 3-6, 6 – 9 9 - 12 12 - 15, f, , 9, , 3, , 5, , 3, , 1, , 25.Draw a less than type of ogive for the given data, C-I, f, , 0-10, 2, , 10-20, 12, , 20-30, 2, , 30-40, 4, , 40-50, 3, , 26.The following distribution gives the daily income of 50 workers of a, factory Convert the distribution above to a less than type cumulative, frequency distribution and, Daily income in RS 100150200250300draw its ogive., 150, 200, 250, 300, 350, No of workers, , 15, , 12, , 10, , 8, , 5, , 27.The following distribution gives the daily income of 50 workers of a factory, Convert the distribution above to a less than type cumulative frequency distribution, and draw its ogive., Daily income in RS, No of workers, , 100-120, 12, , 120-140, 14, , 140-160, 8, , 160-180, 6, , 180-200, 10, , 21
Page 22 :
28, , During the medical check-up of 35 students of a class, their weights were, recorded as follows. Draw a less than type of ogive for the given data ., , Construct” MORE than type of ogive” for the following data, 32, , Weight ( in kg ) Number of students, Less than 38, 0, Less than 40, Less than 42, Less than 44, , 29, , 30, , 31, , More, More, More, More, More, More, , 3, 5, 9, , Less than 46, Less than 48, Less than 50, Less than 52, , 14, 28, 32, 35, , An insurance policy agent found the, following data for distribution of ages of, 35 policy holders. Draw a “less than, type” (below) of ogive for the given, data:, , Daily Income, , Number of workers, , Less than 100, Less than 120, Less than 140, Less than 160, Less than 180, Less than 200, , 0, 8, 20, 34, 44, 50, , 0, , 5, , or, or, or, or, or, or, , equal, equal, equal, equal, equal, equal, , to, to, to, to, to, to, , 50, 55, 60, 65, 70, 75, , frequency, 100, 98, 90, 78, 54, 16, , 2, , Below 25, , 6, , Below 30, , 12, , Below 35, , 16, , Below 40, , 20, , Below 45, , 25, , Below 50, , 35, , The following distribution gives the daily income of 50 workers of a factory., Construct ‘less than ‘type of ogive for given data, <100 <120, , than, than, than, than, than, than, , Age ( in years ) Number of policy holders, Below 20, , The following table gives the information of daily income of 50, workers of a factory. Draw a ‘less than type ogive’ for the given data., , Daily income, (in Rs), No. of, Workers, , The following table gives production yield per hectare of wheat of 100 farms, of a village. Change the distribution to a more than type distribution, and, draw its ogive, Production yield in kg/hectare, Cumulative, , <140, , <160, , <180, , <200, , 15, , 25, , 35, , 50, , 33, , Details of daily income of 50 workersin a food industry are given, below. Drawa more than type ogive for the following data., Daily Income (in Rs.), More than or equal to, 80, More than or equal to, 100, More than or equal to, 120, More than or equal to, 140, More than or equal to, 160, More than or equal to, 180, , Number, of, workers, 50, 38, 24, 16, 10, 0, , 22
Page 23 :
34, , Heights of 50 students of the class X of a school are recorded as follows, Draw a more than type ogive., Height in cm, , 135 - 140, , No of students 5, , Ans:, , 35, , 155 - 160, , 160-165, , 8, , 9, , 12, , 14, , 2, , Coordinats, (x,y), 135,50, 140,45, 145,37, 150,28, 155,16, 160,2, , Change the following distribution to a more than type distribution, and draw, its ogive., CI 0 - 3 3 - 6 6 – 9 9 - 12 12 - 15, 9, , 3, , 5, , 3, , 1, , Change the following distribution to a more than type distribution, and draw, its ogive., 50- 55, 2, , 55 - 60, 8, , 60 – 65, 12, , 65 - 70, 24, , 70 - 75, 38, , 75 - 80, 16, , The following table gives production yield per hectare wheat of 100 farms of a, village draw more than type ogive., Production yield in kg, /hectare, No of farms, , 36, , 150 - 155, , No of, students, 135 - 140, 5, 140- 145, 8, 145 – 150, 9, 150 - 155, 12, 155 – 160, 14, 160-165, 2, Height in cm, Cf, (Lower class limit), more than135, 50, more than140, 45, more than145, 37, more than150, 28, more than155, 16, more than160, 2, , CI, f, , 37, , 145 – 150, , Height in cm, , f, 36, , 140- 145, , Unit 12: SURFACE AREAS AND VOLUMES, , 40-45, , 45-50, , 50-55, , 55-60, , 60-65, , 65-70, , 4, , 6, , 16, , 20, , 30, , 24, , The following distribution gives the daily income of 50 workers of a factory draw its, more than type ogive, Daily income in RS, , 100-120, , 120-140, , 140-160, , 160-180, , 180-200, , No of workers, , 5, , 10, , 20, , 5, , 10, , 1), 2), 3), 4), , Area of the circle= πr2, Perimeter of base of cylinder /cone/ hemisphere=2πr, slant height of cone l=√ 𝑟 + ℎ, slant height of a frustum of cone, l= ℎ + (𝑟1 − 𝑟2), , MMDRS BELAGAVI TOWN -NAGAPPA. KUMBAR., 23
Page 25 :
MINORITY MORARJI DESAI RESIDENTIAL SCHOOL BELAGAVI, TOWN SSLC 2021-22 MATHEMATICS PRACTICS TEST-1, 50 MARKS, 1), CHOOSE THE CORRECT ANSWER, (4X1=4), 1) In an arithmetic progression if an= 2n+1 then common difference of the given, progression is A)0 B)1 C)2 D)3, 2) In the pair of linear equations a1x+b1y+c1=0 and a2 x+b2y+c2=0 if, ≠, A) Equations have no solution, B) Equations have one solution, C) Equations have two solutions., D) Equations have three solutions., 3) A straight line passing through a point on a circle is, A) a Tangent B) a secant C) a Radius D) a Transversal., 4) The distance between the origin and coordinates of a point (x, y) is, A) x2-y2 B) 𝑥 − 𝑦 C) 𝑥 + 𝑦 D) x2+y2., II. Answer the following questions:, (3X1=3), 5) Find the coordinates of the mid points of the line segment joining the points, (x1, y1) and (x2, y2)., 6) Write the formula to find the Total surface area of the frustum of a cone?, 7) If sin A=, find the values of cosec A ?, III. Answer the following questions:, (9x2=18), 8) Find the sum of first 20 terms of arithmetic series 5+10+15+…….. Using, suitable formula., 9) Find the 25th term of an arithmetic progression 2,6,10, 14,…, 10) Solve the pair of linear equations x + y=8 and 2x-y=7, 11) Find the value of the discriminant of the quadratic equation 2x2-5x-1=0, and, hence write the nature of its roots., 12) Solve x2+x-2=0 using formula., 13) In the figure two congruent circles touch each other externally and also touch, the sides of the rectangle ABCD. If AB=28cm and BC=14cm find the area of, the shaded region., A, B, , IV. Answer the following questions (4X3=12), 17) Find the mean of the following data. (Using direct method), C-I 0-2 2-4 4-6 6-8 8-10 10-12, f, 1, 2, 1, 5, 6, 2, , 12-14, 3, , OR Find the mode of following data, C-I, f, , 1-3, 6, , 3-5, 9, , 5-7, 45, , 7-9, 9, , 9-11, 1, , 18) Draw the” less than type ogive”, C-I, f, , 0-3, 9, , 3-6, 3, , 6-9, 5, , 9-12, 3, , 12-15, 1, , 19) Prove that “The tangents drawn to a circle from an external point are equal”., 20) Draw a circle of radius 3 cm. Construct a pair of tangents to it such that the, angle between them is 60°., V.ANSWER THE FOLLOWING QUESTIONS (2X4= 8), 21) Solve the graphically 2x-y=2 4x-y=8., 22) Construct the triangle PQR with sides are QR=4.5cm, PR=3.1cm, PQ 3.3cm, and then construct another triangle whose sides are in the ratio ¾ of the, corresponding side of the give triangle., VI.ANSWER THE FOLLOWING QUESTIONS (1X5=5), 23) State and prove the” Pythagoras theorem.”, , C, D, 14) Find the distance between the two points (2, 3) and (4, 7)., 15) Draw a line segment of AB=8cm and divide it in the ratio 3:2 by geometrical, construction., 16) Construct a tangent to a circle of radius 4cm at any point P on its, circumference., , 25
Page 26 :
MINORITY MORARJI DESAI RESIDENTIAL SCHOOL BELAGAVI, TOWN SSLC 2021-22 MATHEMATICS PRACTICS TEST-2, 55 MARKS, I. CHOOSE THE CORRECT ANSWER, (3X1=3), 1) If the nth term of an arithmetic progression is an=3n+2 then find the 12th term?, , IV. Answer the following questions (5X3=15), 18) Find the mean of the following data. (Using direct, method), OR, , A)38 B)30 C)28 D)20, , 2) In the pair of linear equations a1x+b1y+c1=0 and a2 x+b2y+c2=0 if, = =, A) Equations have no solution, B) Equations have one solution, C) Equations have two solutions. D) Equations have infinitely many solutions., 3) A straight line passing through two points on a circle is, A) a Tangent B) a secant C) a Radius D) a Transversal., II. Answer the following questions:, (4X1=4), 4) Find the distance between the two points are (x1, y1) and (x2, y2)., 5) Write the standard form of quadratic equation?, 6) Write the formula to find the Total surface area of the frustum of a cone?, 7) Find the volume of the sphere, whose radius is 7 cm, III. Answer the following questions: (10x2=20), 8) Find the sum of first 20 terms of arithmetic series 2+7+12+… Using, suitable formula., 9) In an AP 10, 7, 4, ………find 30th term., 10) Solve the pair of linear equations 2x+y=6 and 2x-y=2, 11) Find the value of the discriminant of the quadratic equation x2-2x+3=0 and, hence write the nature of its roots., 12) Solve x 2 7x 12 0 using formula., 13) AB and CD are the arcs of two concentric circles with Centre O of, radius 21 cm and 7 cm respectively. If ∟AOB= 30° as shown in the, figure, find the area of the shaded region., , Find the mode of following data., C-I, f, , 19), , C-I, 0-10, 10-20, 20-30, 30-40, 40-50, , 1-3, 6, , 3-5, 9, , Draw the” less than type, ogive”, , 5-7, 45, C-I, f, , 7-9, 9, 0-10, 2, , 9-11, 1, 10-20, 12, , 20-30, 2, , 30-40, 4, , f, 3, 5, 9, 5, 3, , 40-50, 3, , 20) Prove that “The tangent at any point of a circle is perpendicular to the Radius, , through the point of contact”., 21) Prove that “The tangents drawn to a circle from an external point are equal”., 22) Draw a circle of radius 3.5 cm. Construct a pair of tangents to it such that the, , angle between them is 80°., V.ANSWER THE FOLLOWING QUESTIONS (2X4= 8), 23) Solve the graphically 2x+y=8 and x + y=5., 24) Construct the triangle PQR with sides are QR=4.5cm, PR=4cm, PQ =5cm and, then construct another triangle whose sides are in the ratio 5/4 of the, corresponding side of the give triangle., VI.ANSWER THE FOLLOWING QUESTIONS, (1X5=5), 25) State and prove the “Thales theorem / BPT theorem”, , 14) Find the coordinates of the mid points of the line segment joining the points, (2, 3) and (4, 7)., 15) Draw a line segment of AB=7.6cm and divide it in the ratio 3:2 by, geometrical construction., 16) Draw a circle of radius 4cm constructs a pair of tangents to it from a point 8cm away, , from its center., 17) If sin find the values of cos and tan., , MMDRS BELAGAVI TOWN -NAGAPPA. KUMBAR.-9480345640, 26
Page 27 :
KARNATAKA SECONDARY EDUCATION EXAMINATION BOARD, , 2021-22 SSLC MODEL QUESTION PAPER, Subject: MATHEMATICS, Max. Marks: 80, Subject Code: 81E, Time: 3 hrs. 15 min, I) Four alternatives are given for each of the following questions/incomplete, statement. Choose the correct alternative and write the complete answeralong, with its letter of alphabet., 8x1=8, 1) If a pair of linear equations a1x + b1y + c1=0 ,a2x + b2y + c2=0 in two variables, have unique solution then correct relation among the following is, A), ≠, B) = =, C) =, D) = ≠, 2) The common difference of the Arithmetic progression 100, 93, 86,……….. is, A)4 B)8 C)7 D)-7, 3) If the value of the discriminant of a quadratic equation is zero then thenature of, the roots are, A) Real distinct and irrational B) Real and equal, C)Real distinct and rational D) Not real, 4) The value of cosec 450 is A)1 B)√2 C) D)0, √, 5) The of a point p(x,y) from the origin is, A) 𝒑𝟐 − 𝒒𝟐 B) 𝒑𝟐 + 𝒒𝟐 C) 𝑝 + 𝑞 D) 𝑝 − 𝑞, 6) The empirical relationship between mean, median and mode is, A)3 Median = Mode + Mean B)3 Median = 2 Mode + Mean, C)3 Median = 2 Mode + 2 Mean D)3 Median = Mode + 2 Mean, 7) Which of the following pair of triangles are always similar?, , A) Two isosceles triangles B) Two scalene triangles, C)Two equilateral triangles D) Two right angle triangles, 8) A cone is cut by a plane parallel to its base and the small cone that obtainedis removed, then the remaining part of the cone is, A) a frustum of cone B) a frustum of cylinder C)a Sphere D) a right circular cone, II)Answer the following questions. 8x1=8, 9) In an Arithmetic progression the sum of first four terms is 20 and the sum of first, three terms is 12 then find the fourth term of the arithmetic progression., 10) If a pair of linear equations in two variables are inconsistent then write how many, solutions do they have., 11) Find the value of sin2 + cos2 + 1, 12) A point ‘P’ divides the line joining of points A (x1,y1) and B (x2,y2) in the ratio, m1 : m2 internally then write the co-ordinates of P., 13) State “Pythagoras’s” theorem., , 14) In the figure find the length of an arc AB of a circle, center ‘O’ if∟ AOB= 900, , 15) Write the formula to find the volume of a cone., 16) Find the surface area of a sphere of radius 7cm., III) Answer the following questions. 8x2=16, 17) Solve the pair of linear equations by elimination method.2x + y = 3, 4x – y = 9 OR, Show that the lines represented by linear pair of equations 2x + 3y = 1 and 5x + 6y = 2, are intersecting lines by comparing their co-efficients., 18) Find the 15th term of the arithmetic progression 6, 10, 14using the formula., 19) Find the sum of first 15 terms of 3 + 6 + 9 .................. using the, formula. OR, Verify whether 130 is a term of the arithmetic progression 3, 7, 11 ........., 20) Solve 3x2 – 2x – 3 = 0 by using quadratic formula., 21) Find the value of the discriminant and hence write the nature of roots of the, equation x2 + 3x + 2 = 0, 22) Find the distance between the points (3, 1) and (6, 2) using distance formula., 23) Divide the line segment AB = 10cm in the ratio 2: 3 geometrically., 24) From the given figure. find the value of, a) Sinb) tan, , IV) Answer the following questions. 9x3=27, 25) Prove that “the tangents drawn to a circle from an external point are, equal.”, 26) Find the mean of the, Class Interval Frequency, 27) following data by “direct method”., 10 - 30, 2, OR, 30 - 50, 6, 50 - 70, 10, Find the mode of scores in the following data., 70 - 90, 2, Class Interval Frequency, 1-3, 3-5, 5-7, 7-9, 9 - 11, , 6, 9, 2, 2, 1, 27
Page 28 :
28) Evaluate, 4Sin300 + tan480 .tan420 – 3tan450, OR, 6cos600 – Sin300 + Sin2450 + cos2450, 29), , Yield of co-conuts grown in a village by ‘15’ farmers is as follows. Draw“less, than type” ogive., No. of Co-conuts, less than 50, less than 75, less than 100, less than 125, less than 150, less than 175, less than 200, , Cummulative frequency, 2, 4, 9, 10, 11, 13, 15, , 30) The slant height of a frustum of a cone is 4cm and the perimeters of its circular, ends are 18cm and 16cm, then find the curved surface area of thefrustum of the, cone., OR, A Toy is in the form of a hemisphere surmounted on, a cylinder of height 10cm as shown in the figure., If the radius of the cylinder is 3.5cm find, the volume of the toy., , 31) The sum of 700 is to be used to give seven cash prizes to students of aschool for, their overall academic performance. If each prize is 20 lessthan its preceding prize,, Find the value of each of the prizes., 32) Find the area of a triangle ABC whose vertices are A (2, 2) B (3,4) andC (–1,3)., OR, Find the coordinates of the points of “trisection” of the line joining the, points (6, –2) and (10, 8)., 3 3 )Construct a pair of tangents to a circle of radius 4cm from a point 9cm away from, its center., 3 4 )In the figure ABCD is a square of side 14cm with Centre A,B,C and D four circles, are drawn such that each circle touch externally two of the remaining three circles, as shown in the figure. Find the area of the shaded region, , V)Answer the following questions, 4x4=16, 35) Construct a triangle of sides 6cm, 4cm and 7cm then construct an another, triangle whose corresponding sides are 3/4 of the sides of the first triangle., 36) Solve graphically x + y = 5, x–y=1, 37) The angle of depression from the top of a vertical tower to a point onthe, ground is found to be 600 and from a point 50m above the foot ofthe tower, the angle of depression to the same point is found to be 300 as shown in the, figure find the height of the tower., , 38) A train travels 360 km at a uniform speed. If the speed had been 5 km/h more it, would have taken 1 hour less for the same journey. Find the speedof the train., OR, By selling an article for ` 18.75 a person losses as much percent as it cost, him in Rupees. Find the cost price of the article., VI)Answer the following questions, 1x5=5, 39) State and prove basic proportionality theorem, (Thales theorem)., *******************************************, , 28