Page 1 :
FACTOR, , CHAPTER, , 075), , , , Factor» A number which divides, agiven number exactly is called fac- *, tor (or divisor) of that given numper and the given number is called, , a multiple of that number., , Ex. 1, 2, 4, and 8 are factors of 8, because 8 is perfectly divisible of 1,, 2,4 and 8, , Factors and Multiple, , Ex. Factors of 35 = 1,5, 7, 35, , Ex. Factors of 24 = 1, 2, 3, 4, 6,8,, 12, 24, , } Same,, Multiple of 2 = 2, 4, 6, 8, 10, ., , x Multiple of 7 = 7, 14, 21, 28, 35., he, , *, , Ex.2, , Sol., , , , , , 1 is a factor of every number, , every number is a factor of itself, , every number, except 1 has at, least 2 factor, , L every number has infinite, number of its multiples, a), , }, , every number is a multiple, itself, , , , , %, | Number of Factors ‘sé,, Let N be the composite numf, and a, b, c,.. be its prinfé, fétetor:, and p, q, r be the 2 fee, ae, 18) of a, b, c, i.e, if Red be, expressed as N Per n total number of facts (p + 1), “a+ 1)x 4), 4 is even Pi ‘tor, b and c, are odd Prime, © number of even factors, *(P)* (q+ 1) x (r+ 1), i number of odd factors, 7 1 (q+ yx (r+ 1), Ex.) p;, ™1 Find the total number of fac. EX, cl tors of 8,, " 8 1, 2, 4 and 8 are Perfectly Sol., , divisible, number of factors = 4, , 41Rak,, | sh Yaday Readers Publication Pvt. Ltd., , _ A, , , , This method is easy for, smaller number but for larger, number its a probelm So use, , for alternate method, , Alternate, , 8=2%2x2=28, Number of Total factors, , 2 |240, 21120, 2/160, 230, 3415, 5, , , , ae, , =e yx a+ (+a), =5x2x2=20, , .3*Find the total number of fac, dors of 500., , 21500, , 2 | 250, , 5 | 125, , 5 |25, , 515, 1, , 500 = 2*’2x5x5x5, = 2? «53, , No. of factors = (2 + \)x (3 +1), , =3x4=12, , Number of even Factor, , Find the number of even, factors of 24,, , Factor of 24 = 1,2,3, 4,6,8, 12,24, , Even Factor of 24 = 2, 4, 6, 8,, 12, 24,, , So, ‘ f, Total Ne even Factor, of 24, , Alternate, , }¥ 24 = 23 x 3!, fumber of even factor = 3x(1+1), =3x2=6, Ex.5 Find the number of even factor of 60., 2|60, 2130, 3/15, 515, 1, 60=2x2x3x5, = 22x 31x51, No. of even factor = 2 x (1+1) x (1+1), =2x2x2=8, No. of odd factor, , Ex.6 Find the number of odd factors, of 40., , Sol. 40 = 1, 2, 4, 5, 8, 10, 20, 40, Odd factors = 1,5, , Number of odd factors, , Sol., , =2, , Alternate, , 2/40, , 2/20, , 2/10, , s|5, , 1, , 40= 2x2x9x Ss, , = 23x 5!, , No. of odd Factors= 1 x (l+1), , =1x2, 3. =2, , Ex.7 Find the number of factors,, , number of even factors and, , number of o,, , dd factors of 180, 180, , =2*2x3x3x5, = 2? x 32x 51, Total Number of factors, = @*1)x(2+1)x (1 +1), =3x3x2218, «ffs, , Sol., , Vebi. >

Page 2 :
Number of even factors, =2(2+ Vx (1 +1), =2x3xQ= 12, Number of odd factors, = 1x (2+ 1) x (1 +1), =1x3x2=6, Find the number, number of even fi, , Ex.8, , number of odd factors of 360., 2 |360, 2/180, 2]90, 3145, 3)15, S/S, , 1, , 360 =2x2x2x3x3x5, = 23 x 32x 51, , Total number of factors, =@+1x(2+1x(+1), =4x3x2=24, , Number of even factors, =3x(2+1)x (141), =3x3x2=18, , Number of odd factors, =1x(2+1)x(1+1), =3x2=6, , Ex.9 Find the number of factors,, number of even factors and, , number of odd factors of 100, , 21100, , 2|50, , 5]25, , s]5, 1, , 100 =2x2x5x5 =2?x 52, Total no. of Factor, =(2+1)*(2+1)5 =, No. of even factor= 1), @) 3=6, No. of odd facto; 1W(2 + 1), x3=3, Sum of fa /, Let N be the\gomposite number, and a, b, c,... Be its prime factors, and P, q, © be the indices (or, powers) of a, b, ¢, i.e. if N can be, expressed as N = a?.bi.ch 7, then the sum of all the divifactors) of N, Se +al+a?.... ar) * (b° +b +, V+ CF creas c), b? ....b% * (c°+¢, If a is even prime factor and b, and c odd prime factors then, , , , , , Rakesh Yadav Readers P, , of factors,, lactors and, , = Sum of even factors = (a! + a”, ws a?) x (b° + b! +b? .... ba) x (c°, + OP HGF cscs c'), , = Sum of odd actor = (a°) * (b° +, b! + b?..., by x (c? +c! + 07......C4), , Ex10. Find the sum of all factors of 8., Sol.factors of 8 = 1, 2, 4, 8, Sum of factors = 1+2+4+8, =15, This method is easy for smaller, number but for larger number, its a probelm So use for alter, sum of all factorg, = (2° + 2) + 2? + 9a ,, x (59+ 5), =15*13*6=177, Sum of even factor,, =(2! + 2+ 29) x (30,, x (5° x 5!), = 14% 13 * 6 = 109, sum of odd factors, , HQ x (30+ 32,, =1x * 78, Ex13.find ¢ Ay of |, , sum factors, , nate method odd fas of 100., , Alternate, g=23 24 100, sum of all factors = (2° + 2! + 2? + 23) (%, =14+24+4+8=1 225, wS 15, (a° = 1, where a = real number) 1 100 = 2?;, “ i, , , , , , , , Ex.11find the sum of all 4, , sum of even factors and sum, of, odd factors of 24. . >, , Sol. factors of 24 = 1, 2/3,4%6, 8, 12, 24, sum of factors = +" $3 +4+6, +8+ 12+ 24 = 60m,, sum of even factors, =2 sagt Wola + 24 = 56, , Miebtors = 143-4, , , , , , 24 = 23x 3!, , ‘sum of all factors, = (2° + 2'+ 27 + 29) x (30 + 3), (1+2+4+8) x (1+), =15x4=60, Sum of even factors, = (21 + 22 + 29) x (304 31), = (2 + 4+ 8) x (1 + 3), =14x4=56, Sum of odd factos, = (29) x (3°+ 3) =1x4=4, Ex12.find the sum of all factors ,, , sum of even factors and sum of, odd factors of 360., , Sol. 360, 180, 90, 45, 15, 5, , 1, , UWWNNN, , 360 = 23 x 32x 5), , ublication Pvt. Ltd., , , , ors, |”, , Sum of all factors, = (2°+2'+ 22) x (50+, =7%x31=217, Sum of even factors, = (21 + 22) x (59+ 514, =6* 31 = 186, Sum of odd factors, = (2°) * (59+ 514 54, =1* 31=31, , Prime Factorisation, , Prime Factorisation : I, number is expressed as |, of prime numbers (facto, factorisation of the numt, , its prime factorisation., (i)72, , 2|72, 2/36, 2/18, 319, 313, 1, , 72 = 2x2x2x3x3, 72 = 23x 3?, , number of prime factors, , (ii) 540, , 540, , 270, , 135, , 45, , 15, , Ss, , 1, , 540 = 2 x 2x 3x 3x3, , = 22x 33x 5!, , OAWWWNN

Page 3 :
=>, , No. of prime factor = 2+3+1, =6, ) (ii) find the number of prime factor, 2° x 57x 21* x 10°, gol.2° x 57 x 21x 108, 98 x 57 x (3x 7)" x (2 x 5), Q8 x 57 x Bt x 74 x 28 x 58, , 1 Find the number of Factors of, : 1728 ., of (a)28 (b) 29 (c) 30 (d)31, , g. Find the Number of Factor of, , 1420, , (a}12 (b) 13 (c) 14 @15, 3. Find the Number of Divisors of, , 10800, , (a) 30 (b) 60 (c) 120(d) 180, , 4. Find the No. of Prime Factor of, 240., @4 5 (c)6 (as, , 5. Find the No. of prime factor., (30)?° x (25)! x (12)?, (a)249 (b) 250 (c) 255 (d) 260, 6 Find the No. of Prime Factor, (30)*5 x (22) x (15)?, (a)110 (b) 115 (c) 120 (d) 125, 7. Find the No. of Prime Factor, , , , 180, a4 5 (6 (7, ral, act, he, led, L (a) 3. (b) 5. (a), 2. {a) 4. (c) 6. (b), A, 1 (a, , , , WHWWNNNNNHND, S, oo, , 1728 = 2x2x9x2%2%2x3x3x3, = 26x 33, No. of factors = (6 + 1) x (3 + 1), , Rakesh Yadav Readers Publication Pvt. Ltd., , , , Sol. 6* x8% 10x 12!°, , => (2x3)* x (2x2x2)6 x(2x5)8x(2 x2x3)!?, => 243" x (29)6 x 28 x 5° x (2? x3)?, , => 24 x Bt x 218 x 28 x 58 x 220 x 310, , => QH18+8120 34410 58, , = 250 x 34x 58, , Q" x 34x 515 x 74, Total No. of prime factors, =1144+154+4=34, , Ex14.The Number of prime Factors In, , the expression 6* x8°x 108 12! is, , (a) 48 (b) 64 5, (b) 72 (a) 80 Total Nozet Pome factor, , 8. Find the No. of Prime Factor of (a) 9. Gi) 18,10,8, 536 (c) 18,8, (d) 18,12,6, (a4 (5 (c)6 (a3 15. ie ber 760, 9. Find the No. of prime Factor of ne sum and Number of all, 1044 ss, (a4 (6) 5 (c) 10 (a9 The Sum and Number of, , even factors, (iii) The Sum and Number of, odd factors, 6. For The Number 96, (i) Sum and number of all, factors, (ii) The sum and Number of, , 10. Find The No. of prime factor of, (56) x (36)! x (42)! (13)!, (a) 240 (b) 242 (c) 264 (a) 248, 11. Find the total Number off,, Factors of :, 217 x63! x 75x 10" x ce 213, , , , (a) 142 (b) 144 (c) “ ‘eee 146, even factors, 12. Find the prime Factots ‘ 210 (iii) The sum and Number of, (a)3_(b) 4 (KS, A) 6 odd factors, 13. Find the sum(9f odd factors 17, For the Number 270, 0f544 “fl (i) The sum & Number of all, (a) 16 (b) 10 20 (d)22 Factor, , 14. For the, (Number 2450 find (ii) The sum & Nuniber of, even factor, (iii) The sum .& Number of odd, , Factor, , , , LL ca of odd factors, : y, , , , ANSWER KEY, 7. (b) 9. (b) 11. (¢) 13. (b), 8. (a) [4 10. (c) 12. (b) 14, (a), , =7x4=28, , 3. (b) 10800, , 2 (a) 2/1420 5400, , 2]710 2700, , 5] 355 1350, , 771, , 1, , 1420=2x2x5x71, = 2?« 5! 71!, , No. of factors, , = (2 + 1) x (1+1) x (1+1), , =3x2x2=12, , ANWWWNNNND, a, aq, a, , 10800 = 2x2x2x2x3x3x3x5x5, = 24 x 23 x 52 = 24x 39x 5?, , 15

Page 4 :
No. of factors = (4 + 1) (3 + 1) (2+ 1), =5x4x3=60, , 240, , 120, , 60, , 30, , 15, , 5S, , 1, , 240 = 2x2x2x2x3x5, , = 24x 31x 5), No. of prime factor = 4+1+1=6, (a) (30)?° x (25) x (12)?, Break The form of prime factor, (2!X3 x51) x (5x5)5! x (2x2x3)*, , 4. (ce), , A®omNND, , ”, , Q® x 3% x52 x 5102 x 246 x 3”, , Q26-86 x 326+23 x 5264102, , Yuu y, , Q72 x 349 x 5128, No. of prime factors, 72+ 49+ 128 = 249, (by (30)'> (22) = (15)*, (2x3x5)!5 x (2x11)!! x (3x5)¥*, 235 x 315x515 x QM x] 1! x324x5%, DIS 31524 x 515244] 11, , 2226 x39 x59 x11", No. of Prime factor |, 26 + 39+ 39+ 11=, , Vu Y, , 115, , 7. 2] 180, ™) 3 ]90, , 3/45, 3415, 5|5, 1, , 180=2x2x3%x3x5 ., =2Q2 x 32 x5), No. owe =5, , 8. (a) 2 [536, , 2 pe, 2, 67 7, , \, 536 = 2x22x67 = 2° x 67’, No. of prime factor = 3+1 = 4, , 9. (b) 2/1044, 2)522, 3|261, 3|87, 29 29, , 1, , 1044 = 2x2x3x3x29, = 2? x 3? x 29!, , No. of prime factor 15., , =2+2+1=5, (e) (56)2° x (36) * (42)! * (13)?!, , 10., , => (2X QxQKT PP x (27x37)" x (2 * 3, x7) x (13?!, , => (28 x7} x (264)x(3) x (2 * 3x, 7)8 x (13)!, , 200 x 720 x 262 x 36% QI x 319x719, x13?!, , 00+ 62413 x 362413 x 720813 x 132!, , y, , => 2135 x 375 x 73 x 132!, , Number of prime factors, , = 135+ 75 + 33 + 21 = 264, 11. (c) 2"? x6" 75x 10! x 111° x 21", => QI7 x (2x3)31x 75 x (2x5)! x1 110 x, , (3x7)?, , => 237 x 231x 331x 75x Qi x oe oe, x 32x 72 Me, ginsiert x 33112 x 511 x 75412 10, , 299 x 343x511 x 7H x aK #, Total No. of Prin “Actors, =59+43+ uu + 10, , uu, , , , 21’ = 2'x 31x 5!x 7!, \ =1+14+1+1=4, 13% (b) 544 = 2x2%2x2%2%17, , d = 25x 17!, , Sum of odd factors, = (2°) x (17° + 17!), =1%*(1+17), = 1x 18=18, 14. (a) 2 | 2450, 1225, 245, 49, , 717, , oa, , 2450=2x5x5x7x7, 2450 = 2! x 5? x 7?, Number of Factor = (1 + 1) (2+ 1) (2+ 1), =2x3x3=18, Number of even Factor = 1*@+1)x@+1), =1x3x3=9, Number of odd factor = 1(2+1)x(2+1), =3x3=9, , Nan, , Rakesh Yadav Readers Publication Pvt. Ltd., , =(2, , 0+ 1492, al x (145) x (1+19), , 760, 380, 190, 95, 19} 19, 1, , 760 = 2x2x2x5x19, ='23x5!x19!, , (i) Numbe of factor, , (3+1)a(1Ag)<(1+1), , 4 a, , ANNN, , 1, , ‘tor, 8) x (5° +5!) (19°41, , Sumo, , x20 = 1800, (ii) Number of even factor, =3x(1+1)x(1+1), =3x2x2=12, , Sum of even factor., , =(2' +2? + 29) x (5° + 5!) x (19° +19, = 14 x 6 x 20 = 1680, , (iii) Number of odd factors, =e] x (141) x (141), =1x2x2=4, , Sum of odd factors, , = (2) x (5° + 53) x (19° + 19%), =1x6x20= 120, 16., , 96 = 2x2x2x2x2x3, , = 25 x3!, , (i) Number of all factor, , = (S+1) x (1+1) = 6x 2= 12, , Sum of all factor, , = (2°+2) + 27 +23 +2 +25)x (3°, , = (14+2+4+8+16+32)x(1+3), , = 63 x 4 = 252, , (ii) Number of even factor, , =5x(1+1)=5x2=10, , Sum of even factor, , = (2! + 22423 +2%+25)x(3°+3}), , = (2+4+8+16+32) x (1+3), , = 62 x 4= 248, , (iii) Number of odd factor, =1x(1+1ps1x2=2, , Sum of odd factor, , = (2°) x (39+ 31), , =1x4=4, , II

Page 5 :
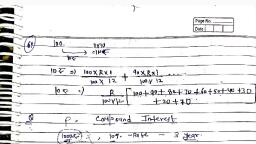
‘0, , 0 17.80l. 21270, , 34135, , ; 3}4s, 31s, SIs, , 2282%5x19 1, , 2°x5'x19", mbe of factor, , 270 = 2x3x3x3x5, = 21x35!, (i) Number of all factor, , , , WO) ¥ (5° +53) ~ a9,, )* 145) = (1+19), = 1800, , amber of even factor, 1+1)x(1+1), , Px 2=12, , f even factor, , B= (5° + 5%) = (19° +199, 0 = 1680, , amber of odd factors, 1+1) = (1+1), , Px 2=4, , f odd factors, , 5} x (19° + 19%), , )= 120, *2x2x2%2*3, , 3, , amber of all factor, jx (11) = 6» 2° 12, , f all factor S, 5 22928 928 022 XO NY, , 4 = 252, , amber of even factoF, W+1)=5%2-10 \, ff even factor y, 22 +2: +24 +2°)x13° 79), , +8+16+32) * (179), , 4= 248, , amber of odd fact?", , \x(l+1p= 17” ae, , f odd factor, , < (3°+ 3°), , t= 4, , +4 +8+16+32)*(179) », , i) 1'"étesh Yaday Readers Publication Pv. Lid., , = (L41)x(3+1)x(1 +1), , = 2x4x2=16, , Sum of all factor, , = (29+21)x(3° +3! +3243) (5945!), =3% 40 = 6= 720, , (ii) Number of even factor, , = 1 (3+1) x (141), =1x4x2=8, , Sum of even factor, , = (2")*(3°+3! +3? +39) * (5° + 5!), =2* 40» 6 = 480, , Number of odd factors, , = 1x(3+1)x(141), , =4x2=8, , Sum of odd factors, =2°x(3°+3!+3243%)x(5°+5!), , = 1x40%6 = 240, , A, e