Page 1 :
sy, , Find t,, and s,, for the following 9., , hs series., 1, B; 15) BBisrevvsssesonns, (a) 64,325 (c) 64,318, (c) 57,325 (a) 57,318, Find t,, and S,, for the following, , series, 2, 8, 14, 20,, (a) 116,1172(c) 110,1180, (c) 116, /1180(d) 110,1172, , 3. Find t,, and s,, for the following, series., , 3, 13, 23, 33 .oeereees, (a) 233,2842 (b) 230,2832, (c) 230,2842 (d) 233,2832, , 4. Find t,, and s,, for the following, series., series - 3, 1, 5, 9,, (a) 65,858 (b) 60,850, (c) 60,868 (d) 65,850, , 5. Find t,, and s,, for the following, series., 30, 33, 36, 39 .., (a) 111,4834 (b) 111,4824, (c) 121,4824 (a) 121,4834, , 6. Find t,, and s,, for the following, series., If 36, 34, 32, 30......, (a) 22,210 (b) -22,210, (c) -22,220 (d) 22, -210, , 7. Find the t,, & S,, for the, following series, 2, 8, 32,, , 10., , , , b) 2, wen 1), , (c) a 2(4 -1), , , , (a) 2 2a “AY ., 3. Find t, {oy the following aa, series. i, 1, »3,9,27.. wy, , 437, (a) 729, 5(3 1), (b) 243, 3(3°-1), (c) 729,5(3" +1) 14., , em, (d) 243, 5(3* +1), , EXERCISE, , Find t,, and s,, for the following 15. How many terms are there In, , series,, 9, 18,9, 55 ssa, iy 1, oof] ool, 1\? 1, (b) 18(3] 36(!-g}, 1\* 1, (c) 18(3| 61-3], : 1" 1, (a) 18(3] 36(1 -z, Find t,, and $4, for the following, series. x, , 64, 16, 4,1, , Find the sum of all numbers, divisible by 6 In 100 to 400, , (a) 12450 (b) 12550, , (c) 12400 (d) 12456, , How many natural Numbers, between 300 to 500 are nultiple, of 7?, , (a) 29 (b) 28 (c) 27 (d)30, Find the value of the, Expression 1-6+2-7+3-8+, to 100 terms, , (a) -250 (b) -500, , (c) -450 (d) -300, , How many terms of the series, -12, -9, -6, ...... must be Taken, that the sum may be 54 ?, , (a) 15 (b) 14 (c) 18 (a) 12, , ‘akesh Yadav Readers Publication Pvt. Ltd., , the A.P 20, 25, 30, ........ 130?, (a) 22 (b) 23 (c) 21 (d)24, 16. Find the Ist terms an A.P. whose, 8th and 12th terms are, respectively 39 & 59, (a)5 (b) 6 Ke) 4 (a3, 17 There is ae 3, 5,, which term of ic AP is 55. ?, , (a) i nets (c) 25 (d) 28", , 18. Find the A5" term of the, sequence 20, 15, 10,, (af45 (b) -50 (c) -55 (d)O, , 7 ‘number 15 is divided In three, , * Gas which are In A.P and The, , fim of their squares is 83., , bd Find the Smallest No., , (a)5 (bh) 3 (c)6 (a8, , 0. The sum of the first 16 terms of, , an A.P. whose first terms and, , third term are 5 and 15, , respectively is, , (a) 600 (b) 765 (c) 640 (d) 680, : The Number of terms of the, , series 54+ 51+ 48+ such, , that the sum is 513 is, , (a) 18 (b) 19, , (c) Both a and b (d) 15, , A man receives % 60 for the, , first week and % 3 more each, , week than the preceding week., , How much does he earn by the, , 20th week ?, , (a) 71770 (b) F 1620, , (c) %.1890 (a) = 1790, , - How many terms are there In, the G.P 5, 20, 80, 320 ........, 20480?, (JS ()6 (7 ds, A boy agrees to work at the rate, of one rupee on the first day,, two rupees on the second day,, four rupees on the third day and, does on. How much will the boy, get if he start working on the, 1st of February and finishes on, the 20th of February ?, , (a) 2” (b) 27-1, , (c) 2-1 (a) 2", , If the Fifth term of a G.P. is, , 81 and first term is 16,, , what will be the 4" terms of, , the G.P?, , (a) 36 (b) 18, , , , , 24., , 25., , (c) 54 (dy 24, , Is
Page 2 :
26. The 4th and 10th term of a GP, , are 1/3 and 243 respecti, Find the 2nd term. Peetively., la) 3 (b) 1, (c) 1/27 (a) 1/9, a eu ae 21th term of an, are 6 and -22 r i, Find the 26th ‘cm,, (a) -34 (b) -32 (c) -12 (d)-10, The sum of 5 number in AP is, 30 and the sum of their, squares is 220, Which of the, following is the third term?, (a5 &)6 (8 @10, The sum of the first four terms, of an AP is 28 and sum of the, first eight terms of the same, AP is 88. Find the sum of the, first 16 terms of the AP?, (a) 346 (b) 340 (c) 304 (d) 268, Find the number of terms of the, =7) J, 81'27'9 29, (a) 11 (b) 12 (c) 10 (d)13, A man saves & 100 in January, 2014 and increases his saving, by = 50 every month over the, previous month. What is the, annual saving for the man in, the year 2014 ?, (a) = 4200 (b) = 4500, (c) 4000 (d) = 4100, What is the maximum sum of, the terms in the Arithmetic, progression, , 27., , 28., , 29., , 30., , series, , 31., , 32., , (a) 6375, , (c) 6625 (a) 650, , 33. An equilateral triangle is, joining the midpointg, of _the, of another equilateral, third equilateral triangle, inside the second ,one joining the, midpoints of the sidés ofthe second, equilateral ‘triangle, and the, , , , , , , , , , , , , , the equilateral triangles, if side of (a) 1080 (b) 720, , the largest equilateral triangle is (c) 900 (d) 620 |, 24 units. 40. The sum of an infinite g, (a) 288 units (b) 72 units whose common ratio }, (c) 36 units (d) 144 units numerically less than 1 is 3!, , 34. Find the value of the and the sum of the first ty 4. th, expression terms is 24. What will be yo, 16+ 2.5 Tt 8-8 Pineve to third term ?, , 100 terms (a) 2 (b) 16 (c) 8 (d)4 |, (a) -250 (b) -500 41. What will be the value,, (c) -450 (d) -300 ni/?, n'/*, m8, oo... 00 ‘, , 35. Find the sum of the Integers (a)? &) ae (o) PP nm, between 1 and 200 that are 42. Deter! i ¢ the first term of t,, multiples of 7 ? geo i ogeression, th, (a) 2742 (b) 2842 sum se first term a,, , (c) 2642 (d) 2546 third term is 40 and the s |, , 36. After striking a floor a rubber ofathe Sécond term and fourg 21, ball rebounds (7/8) of the Agee is 80., height from which it’ has. “(afel2 (b) 8 (c) 16 (a4, fallen Find the total distance%, 48. Yt is G.P 32, 4, 8, n and 2 ay, that it travels before coming to AN \WJG.M is 8, find the value of n, rest, if it is gently dropped from |, (a)2 (b)4 (8 (16, a height of 420 meters.¢ ¢“ 4. Find the Arithmetic mean q, (a) 2940 (b) 6300 \ the following series, (c) 1080 (d) 3360"), 20, 23, 26, 29 3., , 37. Jack and Jil were pl, , , , ying, mathematical puzzles with éach, other. Jill drew a Square of sides 8, cm and then kept’on*drawing, squares inside (the Squares by, joining the pfid points of the, squares. pte continued this, process indefinitely. Jill asked jack, , to determine ‘the sum of the areas, , , , , , , , , , , , ‘would bé his answer ?, (a)128 (b) 64 (c) 256 (d) 32, 38. If the m™ term of an AP is, , iL. i, —and n term is — then find, n m, , \, * the sum to mn" term, , 1, (a) 4(mn-1) o) (mnt), , 1, (c) 3(mn +1) (@) 5(mn-1), , The first and the Last terms, of an A.P. are 107 and 253. If, there are five terms in this, , process continue: finitely. Find :, the sum ‘@fathe perimeters of all sequence, find the sum of, a1 sequence, Y, ANSWER KEY, 1. (a) 6. (b) 11. (a) 16. (c) 21. (c) » (ec), 2. (c) 7. (a) 12, (a) 17. (d) 22. (a) + (b), 3. (d) 8. (a) 13. (a) 18. (b) 23. (c) . (d), 4. (a) 9. (d) 14. (d) 19. (b) 24, (b) » (c), 5. (b) 10. (a) 15. (b) 20. (d) 25. (c) » (a), , , , Rakesh Yadav Readers Publication Pvt. Ltd., , 45., , 46., , + (b), + (a), ~ (d), - (a), ~ (b), , 59 49, , (a) 49 (b) > (c) “> (d)s9, , If the arithmetic mean of th, number X,, X,, 5 x, is}, then the arithmetic mean¢, the number ax,t+ b, ax,* b, ax, b, ax,t+ b, where aandba, two constants, would be ?, , (a) x (b) nax+nb, (c) ax (d) ax+b, A boy draws n squares wit, , sides 1, 2, 3,4, 5, .... in inche, The average area covered b, , , , , , , , , , , , these n squares will be : 5., n+l, (a) (23), 2H\ ="), Oia ( a], n+1)(2n+1)- 6, ie) ew 3 ), n+l 2n+1, @ |= J, 2,, 36. (b) 41. (b) 46. @, 37. (a) 42. (b), 38. (c) 43. (a), 39. (c) 44. (c), 40. (d) 45. (a), , I"
Page 3 :
(CE taees, , (a) 1, 8, 15, 22,, This is A.P series, , 1., , axl, d=@-=7, T.71+(0-1)7=1+63= 64, , 10, Som [2X14+9%7], , =5[2+ 63]=5* 65 = 325, s. (c) 2, 8, 14, 20, a=2, d=6, Ty = 2+19* 6= 116, Sy) = 10 [2 x 2 + 19 x6], = 10 [4+ 114] = 1180, (4) 3, 13, 23, 33, a=3, d=10, T,, = 3 +23 x 10 = 233, S,, = 12 [2 x 3 + 23 « 10], = 12 [6 + 230], = 12 x 236 = 2832, (a)-3, 1,5, 9,.., a=-3, d=1-(-3)=14+3=4, Ti =-3+17*4=65, S,, =11[2*-3+21 x 4], =11[-6 + 84) =78 x 11= 858, , . (b) 30, 33, 36, 39 ......, , , , a=30, , d=3, , T= 30+27x3=121, , S,, = 24 [2 x 30 +47, , = 24 [60 + 141] = 48a, , (b) 36, 34, 32,30, , a= 36, , d=(34, Ty = 36+, = 36-58 ¥-22, , S,, = 15 [2 x 36 + 29 x -2, , = 15 (72 - 58], , = 15 [14] = 210, , (a) 2, 8, 32,, , a=2, , 8, , 3:, , Typ = art = 2(4)20-1 = 2 x (4), , , , , 10., , p= 4, , akesh Yadav Readers Publication Pvt. Ltd., , , , , = 2 x 2% = gas 1", 64] 1-/ +, sled (7), (r>1) “ 7, or, 2(4” _ /, Aa = 2 (4.1) 11. (a) I Term = ag= 102 (where is, 4-1 8 the Ist tefm“greater than 100, (a) 1,3,9,27....., that i 18 by 6), ant Last te than 400, which, 3 is divisi 6 is 396., folug, : mR, T, = 1(3)""'= 3%= 729 108 + 114 ......396, 1(3” -1) 1), a fW102,d=6, S,= “321 =30 -1) fo. of term, 9 (\ - Last term - First term a, (d) 18,9, Dies difference, ans 396-102, =——— +1, pe ew 6, 8 2 294, 24-1 1)" Hog tl=494+1=50, T= 18 i), , 8 = [2102+ 496], , = 25 [204 + 294] = 12450, , , , , , r 1)" 12. (a) First multiple of 7 term (300, 1- (3) to 500) = 301, — Last multiple of 7 term (300 to, 1-1 500) = 497, 7 301, 308, ......... 497, f(y" 497-3, 18) 1-(3) 1 No. of term = er, - = a6|1-3,|, , 196, “7 +1=28+1=29, , (a) 64, 16,4, 1.0..., a= 64 13. (a) 1-6+2-7+3-8+......, 16 1 to 100, d= aa (1 +243... to 50 term), pe i” [Where a = 1, d= 1, n = 50}, Tap = 64 (4) = 64 (4) -(6+7 +8... to 50 term), so 1 [Where a = 6, d = 1, n = 50], = GP ae Both series are In A.P., 1)” Use the formula for sum of an, o#(1-(2) AP,, , S30 =, , S,= 3 [2a+(n-1)a], , II 53
Page 4 :
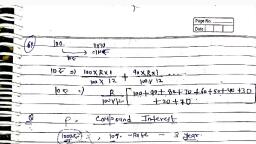
= 25 (2* 1 +24 x 1)- 25 (2 x6 +24 x 1) 18,, = 25 (2 + 24) - 25 (12 + 24), = 25 x 26 - 25 x 36, = 25 (26 - 36) = 25 x -10, = +250, (d) -12, -9, -6,, S,= 54, =-12, d=3, n=?, , 14. 19,, , S, =F at(n-1)a], , 54 = =F 2x42+@-3], , 108 =n [-24 + 3n - 3], , last term = 1= 130, l=a+(n+1)d, 130 = 20+ (n-1)5, 110 =(n-1)5, 22=n~1, n= 23, (c) T, = 39, T,, = 59, T,=a+7d=39, T,, =a+1ld=5, (ii) - (i), 4d=20, d=5, Put unc gle | d (i) equation, at7x5% 39, a=4, (a4) 1,3, 5,, =1, d=2, n” of AP = 55, 55=1+(n-1)2, =(n-1)2, 27=n-1, = 28th, , 16., , , , , , 17., , , , Rakesh Yadav Readers Pu, , 108 =n [8n - 27] 75 + 2d? = 83 Ae, = 20? =8, , 36 =n [n- 9] 7, , Take opti = : = ., e option (d) n = 12, satisfy Thena-d=5-2-K, , =12x3=36 aS, , So: n= 12 a+d=5+2=@°, , 15. (b) 20, 25, 30, ........ 130 20 (al 2, a7 Dy, a= 20 - (d) a, A, a=5, , (b) 20, 15, 10,, a= 20, =-5, T= 20+ 14% -5, T,,= 20-70, T,, = -80, (b) Let three term In A.P., a-d,a,atd, , A.T.Q, , a-d+atatd=15, , 3a=15, , a=5, , and, , (a - d)? + (a)? + (a + d) = 83, , a? + d?- 2ad + a? + a? + d? + 2ad, = 83, , 3a? + 2d?= 83, , Put the value a = 5, 3 x (5)? + 2d? = 83, , , , , , , , , - 2 [2x5+15x5]=8[10+75], , = 680, , (ce) 544514484000., , a=54, d=-3, , S,- 5 Rat tn-1)d),, , 513 = [2 x 54+ (n- 1)(- 3)], , n|p nis, , 513 =, , 1026 = n (111 - 3n), , 342 = n (37 -n), , This is a quadratic equation n, has two values., , In this condition we help, option., , Option Both n= 18, And n= 19,, Satisfy this eauation., , Then (c) option., , [108 - 3n + 3], , plication Pvt. Ltd., , , , , , , 22. (a) First week = a = 60, , second week = 63, , Therefore, , 60, 63, 66..., , a= 60, , d=3, , n=20, , S,, = 10 [2 x 60 + 19x g, = 10 [120 + 57] =, , (ec) 5, 20, 80, 320, , a=5, , 29° A, , oN,, , tg, , ..20th wee, , 23., , , , T=, , T, , 20480 = 5 (4)"", r = = (4)"- 1, YQ 2210-1), , same base comparisi, power., 12=2n-2, n=7, 24. (b) First day = 1, IInd =2, IlIrd =4, Boy does the work = 20, then 1, 2, 4, 8, ..., a=1, rT=2, , , , , , _ 12-3), gsi, (c) T, = ars! = art = 81, , = 27-1, , 25., a =16(given), 16x r=81, , 26., , (i), @, ar 243,, aro 17/3 3
Page 5 :
ro = 243 x 3 = 729, , , , , , , , , Put the value of d, equation (i), , , , , , , , 33. (d) n, r=3 2at3xQe= 14, Put the value r First equation 2a=8, 1 azq, ax @)P= 3 Si 8 [2% 4 +15 x 2] D ., = 8 [8 + 30] = 8 x 38 = 304, axages 30. (aya= 1 c, 81 — 4,, ae a -1/27 . Perimeter of ABC, : d= Tye, 7-3 = 3x gj At, scare ite. — ADE, 2 81 a7 1 Perimeter. DEF = 3 x 12 = 36, s(b)T, at Od = 6 ....fi) 729 = — (.g)n1 DEN BC, D & E mid point of, Ty, 78+ 20d = -22 ..... (i) 81 Cc :, fi) - @ ‘ 729 x 81 = (-3)r 1, {a + 20d) - (a + 6d) = - 22-6 3°x 3 = (gy wn BES. 300, 14d = -28 3% = (gym, d=-2 nD) comparison (\ 1, Put the value d (i) equation 10=n-] Then DF = pac, a+6x-2=6 n=]] 1, a-12=6 31. (b) January Saves EF= > AB, a=18 Febury = 100+ 5, 0 Therefore,, T,, =at+ 25d = 18+ 25 x -9 100+ 150+... 72, 36, 18, oe. oo, = 18-50 2-82 Sum of savin; 1, $. (d) Let the 5 number of a.p _ £ a=72,r=—, a-2d,a-daa+d,a+2d Si. = 6[2 11 * 50] 2, a-Qdt+a-dt+at+at+d+a+oq 6\[209 + 550] ; = =7 =, =30 50 = % 4500 a =e, 5a = 30 32. (a) maximum sum of the :, a=6 “Terms in the A.P. when all 34. (a) 1-6+2-7+3-8+.. to, @- 2d? + (a-dP ++ (a+aP+@+2qp terms will be positive then. 100 terms, = 220 i Pi The above series is a., a? + 4d? - gad + a2 + q2- 2ad + pe a8 combination of Two APs., a+ a?+ d?+ 2adta? + 4q2 4 1 1 1 => (14+2+3+...., + SO terms), 4ad = 220 C 25, 245, 24, 23-, weed Le -(6+7+8 , + 50 terms), 5a? + 10d? = 220 ~ = 25 [2% 1+49« 1-125 (2x 6+, 27424? = 44 : lig 49 x 1)], Put the value a = No. of term = a7 => 25 [51]-25~x 61, (6)? + 2d? = 44, 4 => 25 [51-61] = 25 x — 10 = -250, 36 + 2d? = 44 1 35. (b) Multiple of 7 from 1 to 200, 2d? = g E98 TVA, ccc 196, P=4, = +1=49+1=50, To -1/2 l-a, be ta No. of Term = —~+1, . (ce) S, = 28 5, S,-88 Sum of series l= 196, 8,= 2 [2a + 3d] = 28 Sq" F 2+ 25 +49% 1) a2, 8,= 4 [2a + 7a] = 88 2 aay, 2at+3d=14 | . 51 196 2a+7d= 09 . = 25 [50 - 24.5] = 25 x 2 No. of term = 196-7 ,,, (ii) - 1, 4d=8 a =, 42g = 6375, , akesh Yaday Readers Publication Pvt. Ltd., , No. of term = 1 1-27 41228, , I 55