Page 1 :
286, Vipul'sM Quantitative Methods-1 (B80, Chapter 10, Index Numbers, 10.1 Introduction:, Index numbers are a special type of averages. Averages can be used, to compare two or more series. But we can use them only when two, series are expressed in the same unit. Averages cannot be used if series, are composed of different types of items. In some cases it is difficult to, measure direct variation and relative variations are to be measured. Here, index numbers can be used. Changes in the general price are incapable, of direct measurements. Index numbers were originally used to measure, the change in the price level. Change in the price level indicates the, change in the purchasing power of money. Price level changes inversely, with the changes in the value of money. When the value of money, decreases, the price level increases. Thus index numbers are meant to, study the changes in the effect of such factors which cannot be measured, directly. They are used to measure the changes in almost all fields., 10.2, Uses of Index Numbers:, We can use them to see how far the cost of living has gone up in the, last ten years. We can also measure the change in the industrial, production. Workers' wages are related to cost of living index number., Index numbers give us the idea about real wages. If the index number, goes up their wages are adjusted to a certain extent. Businessmen and, government agencies can study the change in the general price level and, frame their own price policy. Economists have to study the movements, of the general price levels, as also the changes in the specific groups, to, build and test their theories. The index number is the only tool with, which the movements of all the prices can be measured. The price level, is measured in order to control it. Index numbers are indicators of, economic stability of a country and as such must be kept within limits., We can compare the economic conditions of different countries with the, help of index numbers. Indices of industrial production give us the idea, about the progress in industrial fields. Indices of business activity throw

Page 2 :
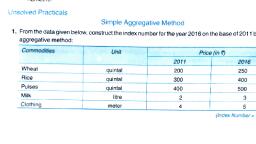
Here the base year relatives are taken as 100. For the other years, o be compared using index number technique. When we see how to, n general economic progress. Index numbers are not used only in, o different periods are given., We start with an example where 3 commodities with their prices for, field. They can be used for comparing two people for their, 287, eN Numbers, on, ht, omic, be dex number, students can easily see how the technique can be, comparing two periods, two persons or two areas in any field., A Basic Concept:, .3, Commodity, per, 1980, Price, unit Rs., 1990, A, 3, 10, 15, 2, 4., Total, 15, 24, We have to measure the change in price level from 1980 to 1990. The, sr 1990 is called the current year and the prices for 1990 are to be, mpared with the prices for 1980, which is called the base year., Three commodities are considered here. The price of each one has, hanged in a different proportion. To measure the change in the price, evel over a period of ten years we must have a single figure., Here the total for 1980 is Rs. 15 and that for 1990 is Rs. 24 and if we, ompare these two, we can see that change is (24/15) x 100 = 160. Here, we compare the prices of 1990 with the prices of 1980. That is, the price, evel of the year 1990 is 160 per cent of the price level of 1980. That is,, ndex for 1980 is 100; index for 1990 is 160., We can see that this method is very simple but is not accurate and it, will not give a true picture of the change in the price level. The first, ifficulty is the unit of measurement. The three commodities may be, aving different units of measurement. If we change the unit of one of, hem, the index number will change., %3D, 0.4 Simple Average of Relatives Method:, To avoid the difficulty encountered in the previous method we, alculate price relatives for each commodity. These relatives are pure, umbers and do not depend upon the unit of the commodity. As a result, Phatever is the unit of measurement for each commodity the index, umber remains the same., latives are calculated as, P1, is the base year's price and pi, x 100 where, Po, Po

Page 3 :
data in the previous example we calculate the index number as follows:, dex Numbers, 289, 288, Vipul'sM Quantitative Methods-1 (BRI, Solution:, Quantities Produced, is the current year's price, ie, current year's prices are expressed, percentage of base year's prices. If the base year's price per unita, Quantities Relatives, Items, Unit, 1990, 1993, 1993, commodity is 2 and current year's price is 3, the price relative isx1oe, 1990, go, 91, x 100, = 150, ie., current year's price is 150 per cent of base year's price, For, Tons, 100, 125, 100, 125, B., Bales, 300, 400, Ex. 1:, 100, 133, Meters, 500, 550, 1980, 1990, 100, 110, Commodity, Price in Rs., Price in Rs., Total, 300, 368, Average Index number, 100, 122.67, Here three commodities produced are measured in three different, aits which cannot be converted in the same unit and direct addition is, mpossible. We could calculate the index number by this method of, average of relatives, because relatives are independent of units, employed., B, 10, 15, 2., 4., Solution:, 1980, 1990, Price Relatives, Commodity, Price in, Price in, Weighted Average of Relatives Method:, 1980, x 100: 1990, po, 10.5, In the above case we calculated simple average of relatives. That is,, all the items are considered to be of equal importance. But in practice all, the items are not equally important. Therefore, changes in the prices of, different commodities do not affect the overall expenditure to the same, extent. We have already seen how weighted average gives the correct, result in such cases., corresponding weights will be discussed later. But here we note that, generally weights for price index number are proportional to quantities, of different commodities and for quantity index number, weights are, proportional to prices of different commodities., We will see how to get index number using weighted average of, Rs. po, Rs. p1, A, 3., 100, 3 x 100 = 167, 10, 15, 100, 15, 10, x 100 = 150, How to determine the importance and, 100, 4, x 100 = 200, 4., Total, 300, 517, Average = Index Number, 100, 172.3, The formula can be written as, relative method:, x 100, po, K, Find the index number using weighted average of relatives, method., Ex. 3:, Por =, where K is the number of commodities., (Nov. 17), Using this method we can also calculate quantity index numbers. If, we have a number of commodities produced in two different periods, each of which has different units of measurement, we can find the index, of production using this method of average of relatives., Quantity, consumed 1980, Price in Rs. per unit, Commodities, 1980, 1990, 10, 10, 15, Ex. 2:, 4, Quantities Produced, Items, Unit, 1990, 1993, Tons, 100, 125, Bales, 300, 400

Page 4 :
ex Numbers, Ehe, 290, Vipel's Quantitative Methods-(, 18305, 119 15382, www, Solution:, P, Price in, Rs. per unit, 1980, Price, Quantity, consumed, 1980, relatives, Weights, Pogete, Commo-, Price in Rs. per unit Quantity, dities, Commodity, 1990, x 100, Pe, 1980, Pe, 1990, 10, 167, 30, 3., in 190, 5010, 3000, 2000, 10010, A., 10, 15, 2., 150, 20, B, 10, 10, 15, 4., 200, 10, 2., Total, 60, 2., olution:, Here the price relatives are calculated and denoted by i. The weights, ane proportional to quantities consumed in the base year. The actual, weights taken are the amounts spent in the base year of different, commodities. We now want weighted average of T with weight w = p., Price in Rs. per unit Quantity, Commodity, 1980, 1990, in 1980, Po, Pi P, 3., 5., 10010, 60, Pa-, 10, 50, 166.8, B, 10, 30, 15, 2., 2., 30, 20, 10.6 Weighted Aggregate Method (Lespeyre's, Paasche's, 5., 20, 10, Total 100, and Fisher's Formulae):, 60, The same result as above can be obtained by a simple method, Por =, x 100, Epogo, x100 x poe, Eite, 100, x 100, x 100, %3D, Pm, Epoto, 60, = 166.7, Ex. 4:, Calculate index number using weighted average of relative, method., This index number is practically the same as the previous one. The, (March 19), ifference is due to the fact that the first price relative x 100 is taken as, Price, Commodities, Quantity 2017, 67 and not as 166.67., 2017, 2018, Eputo, This formula por =, 4., 2., Epogo, x 100 is known as Laspeyre's Formula., B., 3., 5., 5., If instead of base year's quantities current year's quantities are used,, eget, 10, 15, 10, Solution:, Price, Price, Po=, Epon, This is known as Paasche's Formula., x 100, Quantity, 2017, Weights, w = poge, Relatives, Commo-, dities, 2017, 2018, iw, Po, P1, x 100, Po, in Laspeyre's formula we express Eps that is the aggregate, 800, enditure in the current period, as a percentage of the base year's, 2., 4., 2., 200, 4, enditure. We assume that even in the current year the same, antities as base year's are consumed. That, B, 3, 167, 15, 2505, 15000, standard of living is the, In Paasche's formula current year's standard of living is, nsidered., 10, 15, 10, 150, 100, Total, 119, 18305, RRR8

Page 5 :
If we interchange p and q in the above formula we get quantity index, We have one more formula for index number which is important. It is, Laspeyre's index number is defined as Por =, Vipul'sM Quantitative Methods-1 (BBI), ndex Numbers, = 131.09, 293, It should be noted here that, sher's index = V(Laspeyre's index) (Paasche's index), 292, Egipı, F=VLx P, Comparison between Laspeyre's and Paasche's, Index Numbers:, Eape, Eqopi, by, numbers, i.e., Qui = by the Laspeyre's formula and Qui, Paasche's formula., known as Fisher's ideal formula:, Epiga, x 100. Here base, Epogo, Epiga Epigi, x 100, Pon =, Epogo, Epogi, ar's quantities are used. These quantities may not represent the, ansumption pattern for later years. In Paasche's Index we use current, (Oct. 16), Ex. 6:, For the followving data, find Laspeyre's, Paasche's and Fisher's i ), Epigs, vear's quantities. It is defined as por =, Epogi, x 100. This requires selection, numbers., Current Year, of new weights every year, or even month. It is usually impossible to get, aurrent quantities so often. Besides, the amount of calculation is, doubled. In Laspeyre's index, denominator Epogo is fixed and only the, numerator is calculated every year. For Paasche's index both the, numerator and the denominator are to be calculated every year. A more, serious drawback of this method is that, each year is compared to the, base year but comparison among different years is not valid., As price of any commodity increases people try to reduce their, consumption and manage with less quantity or they shift some of their, Base Year, Price, Quantity, Quantity, 20, Commodity, Price, 10, 22, 15, 10, 20, 9, B., 18, 11, 15, C, 6., 15, 10, Solution:, Current Year, Base Year, Commodit, Price, Qty., Pogo Pogi Pr90 Pig1 purchases from commodities showing great relative price increase to, Price, Qty., some substitute commodities whose prices have increased less, 220 drastically. Therefore if we use base year's quantities when prices are, increasing, that index number overestimates the change. On the other, y, P1, 91, po, 8, 10, 22, 160, 176, 200, 20, 135, 180, 150, 200, hand if, 165, underestimates the change because the base year aggregate is not, 90, representative then. If the quantities do not change to a great extent, two, 15, 10, 20, use Paasche's index using current quantities it, we, 11, 15, 126, 105, 198, 18, C, 15, 6., 60, 60, 90, 10, 6., index numbers do not differ significantly., Fisher has suggested a formula which is called Fisher Index Formula., D, Total, 481, 521, 638 675, Laspeyre's index number is, 638, x 100 =, Epiga, Epogo, which is the geometric mean of the, Epigo, Poi =, Epogo, x 100 = 132.64, Por =, Epoq1, previous two indices. But this will require again current year's quantities, and the computation is also more., 10.8 Marshall-Edgeworth and Dorbish-Bowley Index, 481, Paasche's index number is, 675, x 100 =, Epigi, Poi =, Epog, x 100 = 129.56, Numbers:, We also have to consider two more formulae: The first one is known, as Fisher's alternate formula or Marshall-Edgeworth formula., 521, Fisher's index number is, Epigi, Epigo, Epogo Epogi, 638 675, 481 * 521 x 100, Poi =, x 100