Page 1 :
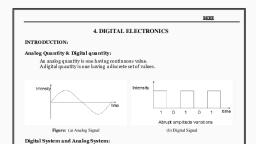
‘Syllabus :, , Number ayatem : Base or radix, Binary arithmetic :, , It, complement, Codes : BCD, Gray code, Excess-3 and ASCII code, BCD arithmetic : BCD addition., , a, , Addition, Subtraction,, , 1.1. Introduction:, , In the modem world of electronics, the term, generally associated with a computer,, , This is because, the term “digital” is derived from the way, computers perform operation, by counting digits., , “digital” is, , For many years, the main application of digital electronics, was only in the computer systems., , But today, the digital electronics is used in many other, applications such as : TV, Radar, Military systems, Medical, -equipments, ‘Communication systems, Industrial process, control and Consumer electronics., , 1.2 Signals: _, , Definition :, , We can define “signal” as a physical quantity, which contains, some information and which is a function of one or more, independent variables,, , The signals can be of two types :, 1. ‘Analog signals 2. Digital signals, , 1.2.1 Analog Signals :, , Definition :, , An analog signal is defined as the signal having continuous, values. They can have infinite number of different values., , Most of the quantities observed in nature are analog. The, examples of analog signal are as follows :, , of number system, Binary,, Multiplication, : Division, Subtraction using 1's complement and 26, , Octal, Decimal and hexadeclmal nenber ‘systom,, , , , 1.2.2 Digital Signals :, , Definition :, , , , 1. Temperature 2. Pressure, 3. Distance 4. Sound, 5. Brightness 6. Voltage, 7. Current 8. Power, , ‘A digits? signal is defined as the signal which has only a, , finite number of distinct values,, , Digital signals are not continuous signal. They are discrete, signals as shown in Fig. 1.2.1,, , Binary signal : If a digital signal has only two distinct values,, i.e. O and 1 then itis called as a binary signal., , , , , , , , , , , , 0 ot, , 0 41 a) 1 ao” 0, (B-2163) Fig. 1.2.1 : Binary signal (Digital signal), , Octal signal : A digital signal having eight distinct values is, , called as an octal signal., , Hexadecimal signal : A digital ‘signal having sixteen distinct \, , values is called as the hexadecimal number, , , , , , , , , , , , , , , , , , Hexadecimal,, , 1.2.3 Sources of Digital Signal :, , The digital signals can be obtained directly from the, computers. All the data used by the computers is digital., , We can also use an A to D converter (Analog to digital, converter) in order to convert analog signals into digital, signals., , , , , , , , , , Scanned with CamScanner

Page 2 :
“logic 1” state and + 5, V, ‘This is called as “negative logic”., , , , 3 Logic 0(LOW) =+5 V, Logic 1 (HIGH) =0 Vrem Logic 25V__ntogic 0,, ate |, r= Logic: ov + Logie 4., (a) Positive togic (b) Negative logic, , (439) Fig. 1.5.1 s}, , , , 1.6 Number Systems 2, , Definition ;, , A number system d, quantity. We talk, the numbe:, Aumbers to, The study o}, , lefines a set of values used to represent a, ‘ about the number of people attending class,, Of modules taken per student and also -use, Present grades obtained by students in tests., We spol f number systems is Not just limited to computers., ver wil eee every day and knowing how numbers, Us an insight i i, and poise a ay sight into how a computer manipulates, , 1.6.1, , Important Definitions :, , Ri, , aa or Base : The number of values that a digit (one, jane) can have is equal to the base of the system. It is, , also called as the Radix of the system,, , For example for a decimal system, the base is “10” because, , every digit can have 10 distinct values, (0, 1,2, scan 9)., , , , 2. The largest value of a digit Is always one less than the, base : For example, the largest digit in a decimal system is 9., (One less than the base 10)., , 3. Weight : Each place (position or column number) represents, , a different multiple of base or radix. These multiples are also, called as weighted values or Weight., ~ That means the numbers have positional importance. For, , example consider the decimal number (349.25),9 shown in, Fig.1.6.1., , , , 3x10" = 3x100 = 300 5x10" = 5/100, , , , (C-5) Fig. 1.6.1 : Numbers have positional importance, , , , , , , , , , , , , , , Where 6 = Base or Rad ., (carFig. 1.62, , Numbering systems :, , .6.2 Varlous : ;, - ing systems used in practice and their bases “>, a, , Various numbe:, are as shown in Table 1.6.1., , , , ystems and their bases, ‘Table 1.6.1 : Various number eat aT, zl, , , , , , , , , , , , , , , , , , , , 10, , 12, Duodecimal 16, Hexadecimal, , , , 1.7 The Decimal Number System :, , Definition :, ‘The number system we have been tnught to use since school is, , called the decimal numbering system., = We are all familiar with counting and mathematics that uses, , this system., = Looking at its make up will help us to understand other, , numbering systems., 1.7.1 Characteristics of a Decimal System :, , ‘Some of the important characteristics of a decimal system are :, , 1, Ituses the base of 10., , 2. The largest value of a digit is 9., , 3. Each place (column number) represents a different multiple, of 10. These multiples are also called as weighted values., The weighted values of each position ure as shown in, Fig. 1.7.1., , , , Decimal point, , , , 10'=0.1, (C-8) Fig. 1.7.1 : Positions and corresponding weighted values, , , , for a decimal system, ¥ TechKnowledg,, , Puctication, , Scanned with CamScanner

Page 3 :
Most Significant Digit (MSD);, , The Ioftmost digit having the'hi, most significant digit of a number,, , Least Significant Digit (LD) :, , The rightmost digit having the lowost Weight Is called og the, least significant digit of n number,, , ighest welght Is called ns the, , Ex..7.4: Represent the decimal number 532, 86 in, , terms of powers of 10,, , Soln.: The required Tepresentation is shown in Fig. P. 1.7.1,, , , , N= Sx 10°49 1042510 48x10 46s 107, (C-9) Fig, PL 1.7.1, , , , , , , , , , , , Definition :, , A number system with a radix 2 is called as the binary number, system., , Most modern computer systems use the binary logic for their, operation. A computer cannot operate on the decimal number, system., , A binary number system uses only two digits namely 0 and 1., The binary number system works like the decimal number, system except one change. It uses the base 2., , Hence the largest value of a digit is 1 and the number of, values a digit can assume is two i.e. 0 and 1., , The weighted values for different positions for a binary, system are as shown in Fig. 1.8.1., , , , |, Binary point, , (C-10) Fig. 4.8.1 : Weights for different positions, for a binary system, , The binary digits (0 and 1) are also called as bits. Thus binary, system is a two bit system., The leftmost bit in a given binary number with the highest, weight is called as Most Significant Bit (MSB) whereas the, rightmost bit in a given number with the lowest weight is, called as Least Significant Bit (LSB)., , Numbar Systems and Codes, Ex. 1.8.1: Exproas tho binary number tor1.0%1 In terme, , of powers of 2,, Soln.:, , Step 1; Express the given number In powers of 2:, , , , 1240x244 het 227402 et ota po, (C-11) Fig. P. 1.8.1, 1.8.1 Binary Numbers from (0),, to (15), :, , The binary numbers representing the decimal numbers from 0, to 15 are shown in the Table 1.8.1,, , , , Table 1.8,1 : Binary numbers upto G5),, , 0000, 0001, 0010, ool, 0100, 0101, 0110, Olli, 1000, 1001, 1010, 1011, 1100, 1101, 1110, lit, , , , 1.8.2 Binary Number Formats :, , We typically write binary numbers as a sequence of bits (bits, is short for binary digits). We have defined boundaries for, , , , , , , , , , , , , , , , , , , , , , , , these bits., — These boundaries are :, ‘Table 1.8.2 : Binary number formats, , Bit df 1, Nibble 4 0101, Byte 8 0000 0101, Word 16 0000 0000 6000 0101, Double Word 32 0000 0000 0000 0000 0000 0008 0000 0101, , , , , , , , , , = Tech Knowledge, publications, , , , i, , Scanned with CamScanner

Page 4 :
8advant : —, ~ They tages Of the Binary System :, , pay, Teauices a yer MDE System has an important ie a, imal ny FY Jong string of 1's and O's to fp!, mber, For example,, ee (128), = (10000000),.-.require 8 bits to represent (128),,, Imagine what will, z (26275) is tobe onvered., s :, deve OM this the other numbering systems were, ' Ped. Let us discuss them one by one.”, 9, Octal Number System 2, , S-11, S-17, I-Scheme : W-18, , , , , , Numbering systems in detail. Al ive), 2 (S14; 8 Marks), , , , Se/radix, digits/symbols and its example”, ~ Octal number * : fe, , , , Definition :, , A number system with a radix 8 is called as the octal number, system,, , The important features of the octal number systems are as follows :, , 1. Base : The Base used for octal number system is 8., , 2 — The number of values assumed by each digit: Each digit ia, the octal system will assume 8 different values from 0 ta 7 (0,, 12s 6.7, , 3. The largest value of a digit : The largest value of a digit ta, the octal system will be 7. That means the octal number, higher than 7 will not be 8, instead of that it will be 10, Table 1.9.1 gives you a clear idea about this., , , , Table 1.9.1 ; Octal numbers, , , , , , , , , , , , , , , , , , , , , , , , , , , , , , 0 1 | 20, , 1 uot 4, , 2 2 | 2, , 3 |, , 4 re es), , 5 15 | 25, , 6 lo |, , i 7 |, , x point (Octal point), , MSB, , , , , , isa, , , , orl La, , , , , , , , (c-13) Fig. 1.9.1 : Weights for different positions for, an octal system, , , , , , ‘This is as, shown, , , , Fr ach aig tx a erent mut of DS, inFig. 19.1., , , , tem =, 1.9.1 . Applications of Octal Sys!, ill need, 1. In order to represent large numbers. We will need a huge, , string of 0's and 1's if the binary system is ee ae, Si she octal system can be used for Fedveing 4, 2 So, “large binary number. aja ee, 3. But it is important, to note that the Oa ine:, : computers internally work strictly with the, and not with the octal structure., 4. The octal structure is used only as the convenience of the, user., in, Ex. 1.9.1: Represont tho octal number 645 In power, of 8., Soln.:, Representation In power of 8:, ne fe} 4]s§, , , , , , , , , , , , L, , °, axer + 4x6 + 5x8, (ety Fly. PAD, , 4.10 Hexadecimal Number System:, , Sh Ree Aes us Tek}, , , , | ., 0.1 Explain four numbaring systoms in datail. Also give, a:xampla of convarsions. (S-11,8 Marks), 0.2 Dascriva following numbar systams with respect to, thelr basa/radix, digits/symbols and Its example :, | 1, Octal number, | 2. Hexadacimal numbar. (5-17, 4 Marks), , , , Definition :, , ce system with a mdix 16 is called as the hexadecimal, , , , , , , system., , tant features of a hexadecimal number system are as, , - Base : The bate of hexadecimal system is 16, , ~ Number of values xssumed by each digit : The number of, , ‘fh, , od by each d, , , , is 16. The values include digits, , , , , , Hence the sikteen, $6789ABC, , , , ugh 9 and lettess ALB, C.D., O1234, , , , , , =, , wy ech Knowledgé, Puptications, , , , ete, , Scanned with CamScanner