Page 1 :
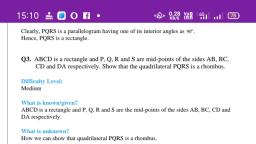
', 5] BYJ U S NCERT Solution For Class 9 Maths Chapter 8- Quadrilaterals, , The Learning App, , Exercise 8.2 Page: 150, , 1. ABCD is a quadrilateral in which P, Q, R and S are mid-points of the sides AB, BC, CD and DA, (see Fig 8.29). AC is a diagonal. Show that:, , (i) SR || AC and SR = 1/2 AC, , PQ=SR, , , , , , (iii) PQRS is a parallelogram., Fig. 8.29, Solution:, (i) In ADAC,, , R is the mid point of DC and S is the mid point of DA., Thus by mid point theorem, SR || AC and SR = % AC, , (ii) InABAC,, P is the mid point of AB and Q is the mid point of BC., Thus by mid point theorem, PQ || AC and PQ = % AC, , , , , , also, SR = 4% AC, -.,PQ=SR, Gii) =SR||AC from question (i), and, PQ || AC from question (ii), = SR || PQ - from (i) and (ii), also, PQ=SR, , ~., PQRS is a parallelogram., , 2. ABCD is a rhombus and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA, respectively. Show that the quadrilateral PQRS is a rectangle., Solution:

Page 2 :
', (as BYJ U S NCERT Solution For Class 9 Maths Chapter 8- Quadrilaterals, , The Learning App, , Given in the question,, ABCD is a rhombus and P, Q, R and S are the mid-points of the sides AB, BC,, CD and DA respectively., To Prove,, PQRS is a rectangle., Construction,, Join AC and BD., , Proof:, In ADRS and ABPQ,, DS=BQ (Halves of the opposite sides of the rhombus), ZSDR = ZQBP (Opposite angles of the rhombus), DR=BP (Halves of the opposite sides of the rhombus), -., ADRS = ABPQ [SAS congruency], RS=PQ [CPCT]---------------------- (i), In AQCR and ASAP,, RC=PA (Halves of the opposite sides of the rhombus), ZRCQ = ZPAS (Opposite angles of the rhombus), CQ=AS (Halves of the opposite sides of the rhombus), «., AQCR = ASAP [SAS congruency], RQ=SP (ecT|-=+--- ae. (ii), Now,, In ACDB,, Rand Q are the mid points of CD and BC respectively., = QR || BD, also,, P and S are the mid points of AD and AB respectively., => PS || BD, => QR||PS, -., PQRS is a parallelogram., also, ZPQR = 90°, Now,, In PQRS,, RS = PQ and RQ = SP from (i) and (ii), 2Q = 90°, , -., PQRS is a rectangle., , 3. ABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA, respectively. Show that the quadrilateral PQRS is a rhombus., Solution:, , , , Given in the question,, , com, , https://by;

Page 3 :
', (s BYJ U S NCERT Solution For Class 9 Maths Chapter 8- Quadrilaterals, , The Learning App, , ABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA, respectively., Construction,, Join AC and BD., To Prove,, PQRS is a rhombus., Proof:, In AABC, P and Q are the mid-points of AB and BC respectively, fs PQ ll AC and PQ = % AC (Midpoint theorem) --- (i), In AADC,, SR || AC and SR = % AC (Midpoint theorem) --- (ii), So, PQ || SR and PQ= SR, As in quadrilateral PQRS one pair of opposite sides is equal and parallel to each, other, so, it is a parallelogram., -., PS |] QR and PS = QR (Opposite sides of parallelogram) --- (iii), Now,, In ABCD,, Qand R are mid points of side BC and CD respectively., ©, QR ll BD and QR = % BD (Midpoint theorem) --- (iv), AC=BD (Diagonals of a rectangle are equal) --- (v), From equations (i), (ii), (iii), (iv) and (v),, PQ = QR=SR=PS, So, PQRS is a rhombus., Hence Proved, , , , , , , , , 4. ABCD is a trapezium in which AB || DC, BD is a diagonal and E is the mid-point of AD. A line is, drawn through E parallel to AB intersecting BC at F (see Fig. 8.30). Show that F is the mid-point of, , , , BC., D c, A B, Fig, 8.30, Solution:, Given that,, ABCD is a trapezium in which AB || DC, BD is a diagonal and E is the mid-point of AD., To prove,, F is the mid-point of BC., Proof,, , BD intersected EF at G., In ABAD,, , russe

Page 4 :
', (Ss BYJ U S NCERT Solution For Class 9 Maths Chapter 8- Quadrilaterals, , The Learning App, , E is the mid point of AD and also EG || AB., , Thus, G is the mid point of BD (Converse of mid point theorem), Now,, In ABDC,, , G is the mid point of BD and also GF || AB || DC., , Thus, F is the mid point of BC (Converse of mid point theorem), , 5. In a parallelogram ABCD, E and F are the mid-points of sides AB and CD respectively (see Fig., 8.31). Show that the line segments AF and EC trisect the diagonal BD., , D F C, , Aye, ss, , A r B, Fig. 8.31, , Solution:, Given that,, ABCD is a parallelogram. E and F are the mid-points of sides AB and CD, respectively., To show,, AF and EC trisect the diagonal BD., Proof,, ABCD is a parallelogram, ., AB || CD, also, AE || FC, Now,, AB = CD (Opposite sides of parallelogram ABCD), =>% AB=%CD, = AE = FC (E and F are midpoints of side AB and CD), AECF is a parallelogram (AE and CF are parallel and equal to each other), AF || EC (Opposite sides of a parallelogram), Now,, In ADQC,, F is mid point of side DC and FP || CQ (as AF || EC)., P is the mid-point of DQ (Converse of mid-point theorem), = DP = PQ -- (i), Similarly,, In AAPB,, , E is midpoint of side AB and EQ || AP (as AF || EC)., , Qis the mid-point of PB (Converse of mid-point theorem), , > PQ = QB--- (ii), , From equations (i) and (i),, , DP=PQ=BQ, , Hence, the line segments AF and EC trisect the diagonal BD., , https://byjus.com

Page 5 :
', (a) BYJ U S NCERT Solution For Class 9 Maths Chapter 8- Quadrilaterals, , The Learning App, Hence Proved., 6. Show that the line segments joining the mid-points of the opposite sides of a quadrilateral bisect, , each other., Solution:, , , , Let ABCD be a quadrilateral and P, Q, R and S are the mid points of AB, BC, CD and DA, respectively., Now,, In AACD,, Rand S are the mid points of CD and DA respectively., <., SRI AC., Similarly we can show that,, PQIIAC,, PS || BD and, QR|| BD, «., PQRS is parallelogram,, PRand QS are the diagonals of the parallelogram PQRS. So, they will bisect each, other., , 7. ABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and, parallel to BC intersects AC at D. Show that, , (i) D is the mid-point of AC, , (ii) MD L AC, , (iii) CM = MA = 2 AB, , Solution:, , https://byjus.com