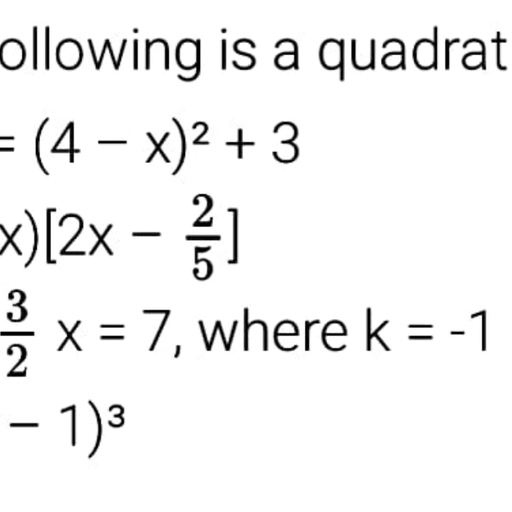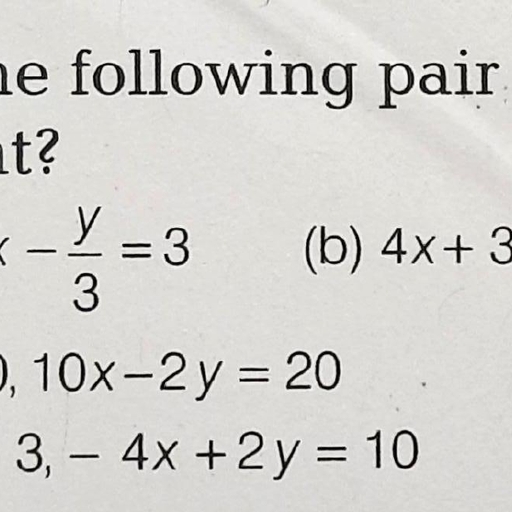Page 1 :
Activity 1, OBJECTIVE, To construct a square root spiral., Materials Required, 1., 2., 3., 4., , Adhesive, Geometry box, Marker, A piece of plywood, , Prerequisite Knowledge, 1. Concept of number line., 2. Concept of irrational numbers., 3. Pythagoras theorem., , Procedure, 1. Take a piece of plywood having the dimensions 30 cm x 30 cm., 2. Draw a line segment PQ of length 1 unit by taking 2 cm as 1 unit., 3., 4., 5., 6., , Construct a line QX perpendicular to the line segment PQ, by using compasses, From Q, draw an arc of 1 unit, which cut QX at C(say)., Join PC., Taking PC as base, draw a perpendicular CY to PC, by using compasses or a, set square., 7. From C, draw an arc of 1 unit, which cut CY at D (say)., 8. Join PD. (see Fig. 1.5)

Page 2 :
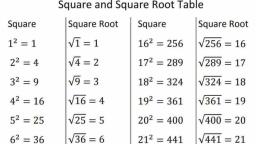
9. Taking PD as base, draw a perpendicular DZ to PD, by using compasses or a, set square., 10. From D, draw an arc of 1 unit, which cut DZ at E (say)., 11. Join PE. (see Fig. 1.5), , Keep repeating the above process for sufficient number of times. Then, the figure so, obtained is called a ‘square root spiral’., Demonstration, 1. In the Fig. 1.5, ΔPQC is a right angled triangle., So, from Pythagoras theorem,, we have PC² = PQ² + QC², [∴ (Hypotenuse)² = (Perpendicular)² + (Base)²], = 1² +1² =2, => PC = √2, Again, ΔPCD is also a right angled triangle., So, from Pythagoras theorem,, PD² =PC² +CD², = (√2)² +(1)² =2+1 = 3, => PD = √3, 2. Similarly, we will have, PE= √4, => PF=√5, => PG = √6 and so on., , Result, A square root spiral has been constructed., Application, With the help of explained activity, existence of irrational numbers can be illustrated., ..............................END...........................

Page 3 :
Now on a separate paper draw a square root spiral and use your creativity to, decorate the square root spiral I’m sharing one example