Page 1 :
Chapter, Chapter, , 15, , Mole Concept,, Number, Stoichiometry, Systems, and Behaviour, of Gases, Remember, Before beginning this chapter, you should be able, to:, • highlight basic concepts of matter and its classification., • understand the concepts of chemical reactions., , Key Ideas, After completing this chapter, you should be, able to:, • derive the formulae of compounds and understand, the naming of compounds., • , study the laws pertaining to the inter-relation of, measurable properties of gases along with ideal gas, equation., • develop numerical ability in mole concept., • learn the types of chemical reactions., • , balance the chemical equations and study the, stoichiometric relation in correlation with the, concept of mole., F I G U R E 1 . 1 Figure, Caption

Page 2 :
5.2, , Chapter 5, , INTRODUCTION, Chemistry is the branch of science which deals with the study of matter. Although the study of matter, involves various aspects, the most important aspect is the study of chemical reactions. A chemical, reaction involves transformation of matter associated with change in molecular composition. For the, sake of convenience and universal application, the chemical reactions are represented in the form of, chemical equations. In these chemical equations, the various substances involved in the reactions are, written in the form of symbols and formulae which are the short-hand notations of the respective, elements and compounds. The study of naming various compounds and derivation of formulae, for the compounds is an inevitable part in the study of chemical reactions, which is considered the, language of chemistry., , SYMBOLS AND FORMULAE, There are 118 elements discovered till now and all of them have been given symbols on the basis of, their English or Latin names. A symbol represents an atom of an element., TABLE 5.1 Examples of symbols, English Names, Name, Chlorine, Carbon, Beryllium, Magnesium, , Latin Names, , Symbol, , Name, Aurum (gold), Argentum (silver), Stannum (tin), Plumbum (lead), , Cl, C, Be, Mg, , Symbol, Au, Ag, Sn, Pb, , The formulae of elements and compounds are written by making use of the symbols of the, respective elements. It represents the actual number of atom(s) of each element present in one, molecule of the substance (element or compound)., TABLE 5.2 Examples of formulae, Names, Nitrogen, Ozone, Barium sulphate, , Formulae, N2, O3, BaSO4, , Radicals or Ions, An atom or a group of atoms gets converted to the corresponding ions or radicals by losing or, gaining electrons. These are called positive and negative radicals, respectively. Based on the, amount/number of charge on the radicals, they are categorised as monovalent, bivalent, trivalent, and tetravalent ions or radicals., TABLE 5.3 Some important positive radicals, Types, Monovalent, Monovalent, Monovalent, Monovalent, Monovalent, , Formulae of radical, H+, Na+, K+, Cu+, Hg+, , Names of radicals, Hydrogen, Sodium, Potassium, Cuprous, Mercurous, , (Continued)

Page 4 :
5.4, , Chapter 5, , Derivation of Formulae of Compounds, Two basic principles are followed in writing the formulae of the compounds. Firstly, the more, electropositive element (positive radical) is written first followed by the electronegative element or, negative radical. Secondly, the total charge on the positive radicals should be balanced by the total, charge on the negative radicals since a molecule is electrically neutral., TABLE 5.5 Compounds and their formulae, Examples, K+ Cl−, 1, , 1, , 1, , 1, , Fe+2, , O−2, , 2, , 2, , Fe+3, , O−3, , 3, , 2, , 2, , 3, , Si+4, 4, , O−3, 2, , 2, 1, , 1, 2, , Ca+2, , NO−3, , 2, , 1, , Formulae, KCl, , FeO, , Fe2O3, , SiO2, , Ca(NO3)2, , 1, , 2, , Naming of Compounds, , Binary Compounds, The compounds that are formed by the combination of two elements are called binary compounds., In naming binary compounds, the electropositive atom (generally metal) is specified first by, giving its ordinary English name. The name of the second element which is generally a non-metal, is obtained by adding the suffix ‘ide’ to its name., Examples:, MgCl2, CaCl2, BaO, H2S, , Magnesium chloride, Calcium chloride, Barium oxide, Hydrogen sulphide, , In case of metals showing variable valency, it is necessary to specify which of the positive ions are, present.

Page 5 :
Mole Concept, Stoichiometry and Behaviour of Gases, , Examples:, FeO, Fe2O3, CuCl, CuCl2, , Ferrous oxide or Iron (II) oxide, Ferric oxide or Iron (III) oxide, Cuprous chloride or Copper (I) chloride, Cupric chloride or Copper (II) chloride, , For binary covalent compounds, generally formed by two non-metallic elements, it is required, to specify the number of atoms of more electronegative element with the help of a meaningful, prefix., TABLE 5.6 Prefixes for binary covalent compounds, Number of atoms, One, Two, Three, Four, Five, Six, Seven, Eight, Nine, Ten, , Prefixes, Mono, Di, Tri, Tetra, Penta, Hexa, Hepta, Octa, Nona, Deca, , The less electronegative element is specified first, followed by the more electronegative element., The prefix is generally added to the more electronegative element to specify its number of atoms., SO2, Sulphur dioxide, N2O5, Nitrogen pentoxide, SF6, Sulphur hexafluoride, PCl3, Phosphorus trichloride, CO, Carbon monoxide, , Naming of Acids, Acids usually contain hydrogen ion (H+) as the positive radical. Hence, the name of the acid is, determined by the constituent(s) of its negative radical., TABLE 5.7 Naming of acids, Types of Acids, Binary acid, , Types of negative radicals, Negative radical consists of a single non-metal, Examples: HCl, HBr, etc., , Oxyacid, , Negative radical consists of a non-metal and oxygen., The name of the oxyacid is determined by the, percentage of the oxygen associated with a specific, non-metal, Acids with comparatively less percentage of oxygen, Examples: H2SO3, HNO2, H3PO3, etc., , Suffixes, ‘ic’ (prefix hydro), Hydrochloric acid, Hydrobromic acid, ‘ous’, Sulphurous acid, nitrous acid, phosphorous acid, , (Continued), , 5.5

Page 6 :
5.6, , Chapter 5, Types of Acids, , Types of negative radicals, Acids with comparatively more percentage of oxygen, Examples: H2SO4, HNO3, H3PO4, etc., , Suffixes, ‘ic’, Sulphuric acid, nitric acid,, phosphoric acid, etc., , If the acid contains lesser number of oxygen atoms than the corresponding ‘ous’ acid, ‘hypo’ prefix, is given to the negative radical, whereas ‘per’ prefix is given to the negative radical when the acid, contains greater number of oxygen atoms than the corresponding ‘ic’ acid., Examples:, Hypochlorous acid, Chlorous acid, Chloric acid, Perchloric acid, , HClO, HClO2, HClO3, HClO4, , Naming of Bases, Bases generally contain hydroxyl radical (OH–) as the negative radical and a metal ion as its positive, radical. While writing the name of the base, the name of the metal is written first followed by, hydroxide., Examples:, Calcium hydroxide, Magnesium hydroxide, Sodium hydroxide, Aluminium hydroxide, , Ca(OH)2, Mg(OH)2, NaOH, Al(OH)3, , Naming of Salts, The positive radical present in the salt comes from the corresponding base and the negative radical, comes from the corresponding acid., The name of the salts starts with the name of the metal present as positive radical which is, followed by the name of the negative radical. The name of the negative radical is determined by the, name of the acid from which the salt is produced., TABLE 5.8 Naming of salts, Acids from which the salt is produced, 1. ‘ous’ acid, Examples:, Sulphurous acid (H2SO3), Nitrous acid (HNO2), Phosphorous acid (H3PO3), 2. ‘ic’ acid, Examples:, Sulphuric acid (H2SO4), Nitric acid (HNO3), Phosphoric acid (H3PO4), , Suffix and name of the salts, ‘ite’, CaSO3, Zn(NO2), Mg(PO3)2, , Calcium sulphite, Zinc nitrite, Magnesium phosphite, , ‘ate’, ZnSO4, NaNO3, AlPO4, , Zinc sulphate, Sodium nitrate, Aluminium phosphate, , If NH4+ is present as a positive radical in the base or in the salt, ammonium is written in place of, the name of the metal.

Page 7 :
Mole Concept, Stoichiometry and Behaviour of Gases, , Examples:, Ammonium hydroxide (base), , NH4OH, , Ammonium phosphate (salt), , (NH4)3PO4, , EXAMPLE, The ratio of number of metal atoms to total number of constituents present in a metal (M), phosphate is 3 : 13. Calculate the total number of constituent atoms present in metal., (i) oxide      (ii) bisulphate      (iii) sulphide, SOLUTION, Let the metal be M and its valency be x, ∴ Metal phosphate = M+x PO4−3 Þ M3(PO4)x, 3, 3, =, The ratio of number of metal atoms to total number of constituents =, 3 + 5x 13, Þ 3 + 5x = 13 Þ x = 2, (i) Metal oxide is M+2O−2 Þ MO, , ∴ Total number of constituents is 2, (ii), , Metal bisulphite is M+2HSO3−1 Þ M(HSO3)2, , , ∴ Total number of constituents is 11, (iii) Metal sulphide is M+2S−2 Þ MS, , ∴ Total number of constituents is 2, EXAMPLE, The valencies of elements A, B, C and D with respect to chlorine in compounds P, Q, R and S are, 3, 4, 1 and 2, respectively. Find out the number of oxygen atoms present in the one molecule of, binary compounds formed by A, B, C and D with same valencies and also mention the formulae, of binary compounds., SOLUTION, The valencies of elements A, B, C and D with respect to chlorine in compounds P, Q, R and S, are 3, 4, 1 and 2, respectively. The formulae of binary compounds with oxygen are A2O3, BO2,, C2O and DO, respectively. So, the number of oxygen atoms present in each molecule of those, oxides is 3, 2, 1 and 1, respectively., A chemical formula gives scope for the study of matter with respect to the molecular composition., The other aspect of the study of matter involves the study with respect to the three distinct physical, states. The three physical states, namely, solids, liquids and gases are basically distinguished on the, basis of their molecular arrangement., Solids are characterised by closely packed molecular arrangement which gives them definite shape., Therefore, the intermolecular forces of attraction are very high in solids. In liquids, the molecules, are relatively loosely packed, and hence, they exhibit less intermolecular forces of attraction. Matter, in gaseous state is characterised by a very loosely packed arrangement of molecules. Due to this, molecular arrangement, there are negligible intermolecular forces of attraction in gaseous state., Consequently, in gaseous state, molecules behave independently, and hence, it is considered the, simplest state of matter., , 5.7

Page 8 :
5.8, , Chapter 5, , Characteristics of Gases Based on the Kinetic Theory of Gases, The postulates of kinetic theory of gases are the following:, 1. Gases contain large number of tiny particles known as molecules., 2. The force of attraction between the molecules is very low., 3. The intermolecular space is large., 4. M,  olecules of a gas are in a state of random motion resulting in continuous collisions among, themselves and with the walls of the container, exerting pressure., 5. The kinetic energy of molecules is proportional to the temperature., From the kinetic theory of gases, we can conclude that the following are the characteristics of gases:, 1. Gases do not possess definite volume and shape., 2. Gases possess low density compared to liquids and solids., 3. Gases exert pressure equally in all directions., 4. Gases are capable of great expansion. They occupy the entire volume of any given container., 5. Gases are highly compressible compared to liquids and solids., 6. Gases exhibit the property of diffusion., The volume and physical behaviour of a given mass of a gas depend on its temperature and pressure over it., Based on experiments, certain relations among the variables of gas (volume, temperature and, pressure) are established. These are stated as gas laws., , Boyle’s Law, The volume of a given mass of a gas is inversely proportional to its pressure at constant temperature., If a given mass of a gas occupies a volume (V) at pressure (P) and temperature (T), then from, Boyle’s law:, 1, V∝, (T is constant);, P, V =, , K, or, P, , PV = K (K is proportionality constant), If at constant temperature, a certain mass of a gas occupies a volume (V1) at pressure (P1), and a, volume (V2) at pressure (P2), then from Boyle’s law, P1V1 = P2V2, at constant temperature., , Graphical Representation of Boyle’s Law, 1. Volume (V) vs pressure (P), , V, , (Constant, temperature), , P, , FIGURE 5.1 P-V curve

Page 9 :
Mole Concept, Stoichiometry and Behaviour of Gases, , 2. Volume (V) vs, , 1, Pressure (P ), , V, (Constant, temperature), , ( 1/P ), , FIGURE 5.2 V-1/P curve, , 3. The product of pressure and volume (PV) vs pressure (P), (Constant, temperature), PV, , P, , FIGURE 5.3 P-PV curve, , NUMERICAL PROBLEM, 1. W,  hat will be the volume of a given mass of a gas at a pressure of 38 cm of Hg if it occupies, 250 mL at a pressure of 114 cm of Hg, keeping temperature constant?, SOLUTION, According to Boyle’s law, at constant temperature,, P1V1 = P2V2,   P1 = Initial pressure,   P2 = Final pressure, V1 = Initial volume, , V2 = Final volume., ,   P1 = 38 cm of Hg , , P2 = 114 cm of Hg, , V1 = ?     , 38 V1 = 114 × 250, V1 =, , 114 × 250, = 750 mL, 38, , V2 = 250 mL, , 5.9

Page 10 :
5.10, , Chapter 5, , Charles’ Law, At constant pressure, the volume of a given mass of a gas increases or decreases by (1/273) of its, volume at 0°C for every 1°C increase or decrease in temperature, respectively,, t °C , i.e., Vt = V0  1 +, , 273 , Let the volume of a given mass of the gas at 0°C be V0. Its volume increases to Vt at t°C under, constant pressure., Hence, from Charles’ law,, Vt = V 0 , , , 273 + t °C , 273 , , T , ; T is the absolute temperature (Kelvin temperature), Vt = V 0 ,  273 , V ∝ T, as, , V0, = constant, 273, , Hence, Charles’ law can also be stated as follows:, For a fixed mass of gas, the volume of a gas (V) is directly proportional to the absolute temperature, (T), at constant pressure,, i.e.,, V ∝ T (P is constant), or, , V, = K (K is the proportionality constant), T, , If at constant pressure, a certain mass of a gas occupies a volume (V1) at temperature (T1) and a, volume (V2) at temperature (T2), then according to Charles’ law:, V1 V2, =, (at constant pressure), T1 T2, , Graphical Representation of Charle’s Law, 1. Volume (V) vs absolute temperature (T), , V(mL), , 0, , (Constant, pressure), , T(K), , FIGURE 5.4 V-T(K) curve

Page 11 :
Mole Concept, Stoichiometry and Behaviour of Gases, , 2. Volume (V) vs temperature (t) in Celsius scale, , V(mL), , (Constant pressure), , t (°C), , 0 °C, , − 273 °C, , FIGURE 5.5 V-t(°C) curve, , From Charle’s law:, , V t = Vo , , , 273 + t °C , 273 , , As t in this equation approaches 273ºC, the volume approaches zero. Below 273ºC, the volume, of a gas would become negative which is an impossible result., Therefore, 273°C is the lowest temperature that can be attained theoretically. However, practically, before reaching this temperature itself all gases either get liquefied or solidified. Therefore, 273ºC is, taken as zero point on a new temperature scale called absolute temperature scale., Temperature in Kelvin scale can be obtained by adding 273 to the temperature measured in the, Celsius scale., T (Kelvin) = 273 + ºC (Celsius), NUMERICAL PROBLEM, (i) A,  t what temperature will a given mass of a gas occupy a volume of 75 L if it occupies a volume, of 100 L at a temperature of 27ºC, pressure remaining constant?, SOLUTION, According to Charle’s law at constant pressure, V1 V2, =, T1 T2, Where, V1 = Initial volume, , V2 = Final volume, , T1 = Initial temperature, , T2 = Final temperature, , Given,, V1 = 75 L, , V2 = 100 L, , T1 = ?, , T2 = 300 K, , V1 V2, =, T1 T2, 75 100, ;, =, T1 300, , T1 =, , 300 × 75, = 225 K, 100, , 5.11

Page 12 :
5.12, , Chapter 5, , The Gas Equation, For a given mass of a gas, the gas equation gives a relationship among the volume, pressure and, temperature, and can be derived by combining the laws of Boyle and Charles., The volume of a given mass of a gas is (V) at temperature (T) and pressure (P)., 1, Applying Boyle’s law: V ∝, (T is constant), (1), P, Applying Charles’ law: V ∝ T (P is constant), (2), Combining (1) and (2),, 1, V∝, T (when both T and P change), P, T, V=K, P, PV, = K (K is a proportionality constant), T, If the volume of a given mass of a gas changes from V1 to V2, pressure from P1 to P2 and, PV, PV, temperature from T1 to T2, then from the gas equation, we have 1 1 = 2 2 ., T1, T2, NUMERICAL PROBLEM, (i) A,  given mass of a gas occupies 143 cm3 at 17ºC and 700 mm of Hg pressure. What will be its, volume at 27ºC and 280 mm of Hg pressure?, SOLUTION, From gas equation:, PV, PV, 1 1, = 2 2, T1, T2, P1 = 700 mm, , P2 = 280 mm, , V1 = 143 cm3, , V2 = ?, , T1 = 290 K , , T2 = 300 K, , 700 × 143 280 ×V2, =, 290, 300, V2 =, , 300 × 700 × 143 2100 × 143, =, = 369.8 cm 3, 280 × 290, 28 × 29, , Standard Temperature and Pressure or, Normal Temperature and Pressure, Temperature and pressure have great influence on the volumes of gases. It is necessary to choose a, suitable value of each as standards to refer to the volume of a gas., The conditions of standard temperature and pressure are given below:, Standard temperature = 0°C = 273 K, Standard pressure = 760 mm of Hg (mercury), = 76 cm of Hg = 1 atm

Page 13 :
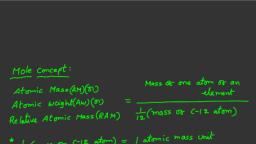
Mole Concept, Stoichiometry and Behaviour of Gases, , A gas which strictly obeys the gas equation under all the conditions of temperature and pressure, is called an ideal gas. However, in nature all gases are real gases, i.e., they do not perfectly obey the, gas equation under all the conditions of temperature and pressure., The behaviour of gases can be expressed by the laws of Boyle and Charles when the gases are, subjected to change in pressure and temperature. Another law, namely, Gay-Lussac’s law of combining, volumes describes the relationship among the volumes of gaseous reactants and products., , Gay-Lussac’s Law of Combining Volumes of Gases, When gases react chemically, they do so in volumes which bear a simple whole number ratio to each, other and to the volumes of the products, provided the products are also in the gaseous state and the, temperature and pressure of the reactant and product gases are the same., Example:, In the reaction of carbon monoxide with oxygen, two volumes of carbon monoxide react with one, volume of oxygen to give two volumes of carbon dioxide:, CO + CO + O2 , → CO2 + CO2, 2 vol, , 1vol, , 2 vol, , The volume ratio of carbon monoxide, oxygen and carbon dioxide is 2 : 1 : 2., In 1811, Amedo Avogadro established a relationship between the volumes of gases and the, number of molecules present in them provided the volumes are measured at similar conditions of, temperature and pressure., Avogadro’s law: Under similar conditions of temperature and pressure, equal volumes of all gases, contain equal number of molecules., Explanation: Under similar conditions of temperature and pressure, 1 L of any gas, hydrogen,, helium or hydrogen chloride contains the same number of molecules., From Avogadro’s law, the number of particles present in a given mass of a substance (solid, liquid, or gas) and the volume of the substance if it is in gaseous state, is calculated., The mass of a substance is nothing but the total mass of its constituent particles, i.e., atoms or, molecules., , Measurement of the Mass of Atoms and Molecules, , Atomic Weight or Relative Atomic Mass, 1, th of a carbon-12 isotope has been taken as the standard. The mass of the atoms of, 2, other elements is calculated with respect to the number of times an atom of an element is heavier, 1, than th part of the carbon-12 isotope. This is called atomic weight or the relative atomic, 2, 1, mass. Since the weight of th part of the carbon-12 is called atomic mass unit, the relative, 2, atomic mass is expressed in amu., The mass of, , Gram Atomic Weight or Gram Atom, The relative atomic mass expressed in grams is called gram atomic weight (GAW) or gram atom., Example: Atomic weight of oxygen = 16 amu, Gram atomic weight of oxygen = 16 g, , 5.13

Page 14 :
5.14, , Chapter 5, , Molecular Weight or Relative Molecular Mass, Molecular weight is a number which indicates how many times, a molecule of a substance is heavier, 1, in comparison to th the mass of one carbon-12 isotope., 2, , Gram Molecular Weight, Molecular weight expressed in grams is called gram molecular weight., The molecular weight of a substance can be easily determined from its formula by adding up the, atomic weights of its constituent atoms., Example:, Calculation of molecular weight of calcium carbonate (CaCO3):, Atomic weight of calcium is 40 amu, Atomic weight of carbon is 12 amu, Atomic weight of oxygen is 16 amu, Molecular weight of calcium carbonate, = 40 + 12 + (16 × 3) = 100 amu, Gram Molecular Volume: One gram molecule of any dry gas at standard, temperature and, pressure (STP) occupies the same volume, i.e., 22.4 L or 22.4 dm3. This is called gram molecular, volume or GMV., Example:, 1 g molecule of dry chlorine gas occupies 22.4 L at STP., Since GMW of chlorine is 71 g, 71 g of chlorine gas occupies 22.4 L at STP., , Avogadro’s Number and Mole Concept, Mole is the unit of amount of substance and it is a number like dozen. By using mole as a unit of, amount of substance, it is possible to calculate the number of atoms, molecules and ions of a given, mass of a substance., , Mole, Mole is defined as the amount of substance that contains the same number of units (atoms, molecules, or ions) as there are atoms in exactly 12 g of carbon-12 isotope. This number is called Avogadro, number. One mole of any substance contains Avogadro number of chemical units., Experimentally, it was found that this number is 6.023 × 1023., From the concept of mole, it can be concluded that:, 1. 1 g atom of any substance is equivalent to one mole of atoms of that substance and contains, Avogadro number of atoms., 2. 1 g molecule of any substance is equivalent to one mole of molecules of that substance and, contains Avogadro number of molecules., Examples: (i), , , (ii), , , , One mole of hydrogen atoms, 6.023 × 1023 hydrogen atoms, 1 g of hydrogen, One mole of carbon atoms, 6.023 × 1023 carbon atoms, 12 g of carbon

Page 15 :
Mole Concept, Stoichiometry and Behaviour of Gases, , (iii), , , (iv), , , (v), , , (vi), , , , One mole of NaCl, 6.023 × 1023 Na+ ions and 6.023 × 1023 Cl– ions, 58.5 g of NaCl, One mole of ammonia gas, 6.023 × 1023 ammonia gas, 17 g of NH3, One mole of sodium, 6.023 × 1023 hydrogen molecules, 23 g of sodium, One mole of hydrogen, 6.023 × 1023 hydrogen molecules, 2 g of hydrogen, , Relation between GMV, mole and Avogadro number: One gram molecule of any dry gas, occupies 22.4 L volume at STP. Hence, 22.4 L of a dry gas at STP is equivalent to 1 mole of that gas, and contains 6.023 × 1023 molecules, i.e., Avogadro number of molecules., Example: 1 gram molecule or 32 g or 1 mole of dry oxygen gas occupies 22.4 L at STP and contains, 6.023 × 1023 molecules of oxygen., Example: 1 gram molecule or 4 g or 1 mole of dry helium gas occupies 22.4 L at STP and contains, 6.023 × 1023 atoms because helium is a monoatomic gas., For all solid and liquid substances, mole can be converted into weight or number of atoms or, molecules. For gaseous substances, mole can also be converted into volume in addition to weight, and number of particles., Examples: (i) One mole of bromine liquid, , 6.023 × 1023 bromine molecules, , 160 g of bromine, (ii), , , , , One mole of chlorine gas, 6.023 × 1023 chlorine molecules, 71 g of chlorine, 22.4 L chlorine at STP, , Schematic Representation of Different Relationships for Mole, , GAW or GMW of an, element or compound, , Mole, , Avogadro number of atoms, or molecules (6.023 × 1023), , GMV, (22.4 L at STP only for gases), , FIGURE 5.6 Different relationships for mole, , 5.15

Page 16 :
5.16, , Chapter 5, , NUMERICAL PROBLEM, (i) Calculate the number atoms present in 112 g of N2 and also find its volume at STP., SOLUTION, Gram molecular weight of N2 = 28 g., 112, = 4 moles of nitrogen, 112 g of N2 is equivalent to, 28, 112 g of N2 contains 4 × 6.023 × 1023 molecules = 24 × 1023 (approx) molecules, The volume of the given mass N2 = (4 × 22.4) L = 89.6 L at STP, (ii) C,  alculate the mass of water which contains the same number of molecules as that of 667.5 g, of aluminium chloride., SOLUTION, Molecular weight of aluminium chloride (AlCl3) = 133.5, 667.5, 667.5 g of aluminium chloride is equivalent to, = 5 moles of aluminium chloride., 133.5, Numbers of molecules present in 667.5 g of aluminium chloride is equivalent to that present in, 5 moles of water., The mass of 5 moles of water = 18 × 5 = 90 g, Another characteristic property shown by gases is the process of diffusion. The spreading of the, fragrance of perfumes in a specific area can be attributed to this property of gases., The volume of the gas diffused in unit time at certain temperature and pressure through unit area is, called rate of diffusion of the gas., Thomas Graham based on his observations, established a quantitative relationship between the, rate of diffusion of gases and their densities., Graham’s law of diffusion states that the rates of diffusion of different gases are inversely proportional, to the square roots of their densities, under similar conditions of temperature and pressure., , Graham’s Law of Diffusion, r=, , 1, (constant temperature and pressure), d, , r1, d, = 2 =, r2, d1, , M2, M1, , NUMERICAL PROBLEMS, (i), , 4 80 cc of methane gas diffused in 40 min. If 1440 cc of another gas diffused in 60 min, under similar conditions of temperature and pressure, then find out the molecular mass of, the gas.

Page 17 :
Mole Concept, Stoichiometry and Behaviour of Gases, , SOLUTION, Rate of methane and unknown gas can be given as, rmethane =, , Vmethane, time, , rmethane =, , 480, = 12 cc / min, 40, , rx =, rCH4, rx, , =, , rx =, , Vx, time, , 1440, = 24 cc / min, 60, Mx, M CH4, , M x 12, =, 16, 24, 12 2, = M x = 2 × 16 = 4 g, 24, =, , Gram molecular mass of the gas = 4 g, (ii), ,  ind out the relative rates of diffusion of oxygen and sulphur dioxide gases under similar, F, conditions of temperature and pressure., , SOLUTION, rO2, rSO2, (iii), , =, , M SO2, M O2, , =, , 64, = 2 :1, 32, ,  olume of a gas was 600 cm3 at atmospheric pressure. Calculate the new volume when, V, pressure increases by 25%., , SOLUTION, Initial pressure of gas (P1) = 760 mm, 25% of initial pressure = 25 × 760/100 = 0.25 × 760 = 190 mm, Final pressure (P2) = 760 + 190 = 950 mm, Initial volume (V1)= 600 cm3; Final volume (V2)= ?, According to Boyle’s Law, P1 V1 = P2 V2 Þ V2 =, (iv), , PV, 760 × 600, 1 1, =, = 480 cm3, P2, 950, , A gas cylinder is filled with hydrogen gas which weighs 40 g. The same cylinder holds, 880 g of a gas A and 560 g of a gas B under the same conditions of temperature and, pressure. Calculate the relative molecular masses of A and B., , SOLUTION, Since the volume of cylinder is same for all gases, they contain same number of molecules that, means equal number of moles under the same conditions of temperature and pressure., 2 g of hydrogen ® 1 mole; 40 g of hydrogen ® 20 moles; 880 g of gas A also constitutes 20 moles, , 5.17

Page 18 :
5.18, , Chapter 5, , Mass of gas A corresponding to 1 mole =, , 880, = 44 g \ Molecular mass of A = 44, 20, , 560 g of gas B also constitutes 20 moles, Mass of gas B corresponding to 1 mole =, , 560, = 28 g \ Molecular mass of B = 28, 20, , EXAMPLE, Equal masses of four different gases A, B, C and D are taken in separate containers of same volume., The molecular masses of the gases are in the order B < D < A < C. Compare the pressures exerted, by the respective gases at constant temperature., SOLUTION, The pressure exerted by a gas depends upon the number of molecules present in the given amount, of gas. The greater the molecular mass, the lesser the pressure exerted by the gas. Since the order of, molecular masses is B < D < A < C, the order of number of molecules could be C < A < D < B., The pressures exerted by the gases is also in the same order., , STOICHIOMETRY, The chemical reactions are represented in the form of chemical equations. Since these chemical, equations should comply with the law of conservation of mass, they should be balanced with respect, to the number of atoms of each element involved in the reaction. Therefore, a quantitative relationship, can be established between the various reactants and products. The area of study pertaining to the, study of this quantitative relationship among reactants and products is called stoichiometry., Example of a balanced chemical equation: NaOH + HCl → NaCl + H2O, Reactants, One atom of sodium, One atom of chlorine, One atom of oxygen, Two atoms of hydrogen, , Products, One atom of sodium, One atom of chlorine, One atom of oxygen, Two atoms of hydrogen, , Balancing of Chemical Equations by Trial and Error Method, 1. T,  he number of times an element appears on the reactant side and the product side of the, equation is counted., 2. The element which appears the least number of times is balanced first., 3. The other elements are balanced in the increasing order of their frequency., 4. In case any two or more elements have the same frequency, the metallic element is balanced, first in preference to the non-metallic element., Example:, Skeleton equation, KI + H2SO4 + MnO2 → KHSO4 + MnSO4 + H2O + I2, Balancing sulphur, 2KI + 3H2SO4 + MnO2 → 2KHSO4 + MnSO4 + H2O + I2

Page 19 :
Mole Concept, Stoichiometry and Behaviour of Gases, , Balancing oxygen and hydrogen, 2KI + 3H2SO4 + MnO2 → 2KHSO4 + MnSO4 + 2H2O + I2, A balanced chemical equation provides, 1. weight–weight relationship of the reactants and products., 2. weight–volume relationship when some of the reactants and products are in gaseous state., 3. volume–volume relationship when all the reactants and products are in gaseous state., , Chemical Calculations Based on Weight–weight Relationship, EXAMPLE, What is the amount of NH3 formed when 14 g of N2 combines with 6 g of H2?, SOLUTION, N2, +, 3H2, →, 2NH3, 1 mol, 3 mol, 2 mol, 28 g, 3×2g, 2 × 17 g, From the balanced equation, 1 mol of N2 reacts with 3 mol of H2 or 28 g of N2 reacts with, 6 g of hydrogen. The amount of nitrogen is less than that required for complete reaction with H2., Hence, N2 is called limiting reactant or limiting reagent. However, H2 is an excess reactant., Further, 28 g of N2 forms 34 g of NH3, 14 × 34, g of NH3, 28, Amount of ammonia formed = 17 g, 14 g of N2 forms, , Chemical Calculations Based on Weight–Volume Relationship, EXAMPLE, When calcium carbonate is strongly heated, 28 g of calcium oxide is obtained, calculate the, volume of CO2 liberated at STP., CaCO3 ∆, → CaO + CO2, SOLUTION, The above chemical equation shows that 1 mole of CaCO3 decomposes to form 1 mole of CaO, and 1 mole of CO2., Hence, if 56 g of CaO is obtained by heating CaCO3, the volume of CO2 liberated is 22.4 L or, dm3 at STP., 28, Therefore, when 2g of CaO is obtained, the volume of CO2 is  22.4 ×  L = 11.2L or dm3., , 56 , , 5.19

Page 20 :
5.20, , Chapter 5, , Calculations Based on Volume–Volume Relationship, EXAMPLE, Calculate the volume of CO2 at STP, when 22.4 L of CO under STP completely burns in the, presence of excess oxygen., 2CO + O2 → 2CO2, SOLUTION, The above chemical equation shows that 2 gram molecular volume of CO reacts with 1 gram, molecular volume of O2, and hence, 2 gram molecular volume of CO2 is produced., Hence, (22.4 × 2) = 44.8 L of CO at STP burns in oxygen and produces (22.4 × 2) = 44.8 L of, CO2 at STP, Therefore, 22.4 L of CO at STP on complete combustion gives 22.4 L of CO2., , Calculation of Empirical and Molecular Formulae of Compounds, Another important aspect of stoichiometry is the elemental analysis of a substance. The proportion by, mass of each element present in a compound is called its percentage composition. The elemental, analysis helps to determine the mass of each element present in 100 g of known compound and it, also establishes the chemical formula of unknown compound., Percentage of an element by mass present in a compound, =, , mass of element in one mole of the compound, × 100, gram molecular mass of the compound, , The chemical formula of the compound that can be calculated from the elemental analysis data, (percentage by mass of each element in the compound) is called empirical formula., Empirical formula represents the simplest whole number ratio of the atoms of different constituent, elements present in one molecule of the compound. The molecular formula of a compound can be, calculated if both the empirical formula and the molecular mass are known., Molecular formula represents the actual number of atoms of different constituent elements present, in one molecule of the compound., The molecular and empirical formula of any chemical compound are related as, n × Empirical formula = Molecular formula, where n is a positive integer, n=, , Molecular mass of compound, Empirical formula mass, , NUMERICAL PROBLEM, (i) Calculate the percentage composition of calcium bicarbonate., GMM of calcium bicarbonate [Ca(HCO3)2] = 162, Amount calcium in 162 g of calcium bicarbonate = 40

Page 21 :
Mole Concept, Stoichiometry and Behaviour of Gases, , 40 × 100, = 24.7%, 162, Amount of hydrogen in 162 g of calcium bicarbonate = 2 g, Amount of calcium in 100 g of calcium bicarbonate =, , 2 × 100, = 1.23%, 162, Amount of carbon in 162 g of calcium bicarbonate = 24 g, , Amount of hydrogen in 100 g of calcium bicarbonate =, , 24 × 100, = 14.8%, 162, Amount of oxygen in 162 g of calcium bicarbonate = 96 g, 96 × 100, Amount of oxygen in 100 g of calcium bicarbonate =, = 59.2%, 162, Percentage composition of calcium bicarbonate, Percentage of calcium 24.7%, Percentage of hydrogen 1.23%, Percentage of carbon, 14.8%, Percentage of oxygen, 59.2%, Amount of carbon in 100 g of calcium bicarbonate =, , (ii) An organic compound on analysis has been found to have following percentage composition:, Percentage of carbon = 40%, Percentage of hydrogen = 6.66%, If the vapour density of the compound is 30, find out the molecular formula of the compound., SOLUTION, Elements, Carbon, , Percentages, 40, , Atomic masses, 12, , Atomic ratios, 40/12 = 3.33, , Simplest ratios, , 3.33, =1, 3.33, , Hydrogen, , 6.66, , 1, , 6.66, = 6.66, 1, , 6.66, =2, 3.33, , Oxygen, , 53.34, , 16, , 53.34, = 3.33, 16, , 3.33, =1, 3.33, , Empirical formula is CH2O, Vapour density = 30 Mol. wt = 2 × vapour density = 30 × 2 = 60, Empirical formula wt = 30, , 60, = CH 2O2, 30, = C 2 H 4 O2 ., , Molecular formula = CH 2O, , 5.21

Page 22 :
5.22, , Chapter 5, , EXAMPLE, Calculate the volume of CO2 formed at STP and the weight of zinc oxide formed in grams, when, 2.32 g of zinc carbonate decomposes with no further loss in weight., SOLUTION, ZnCO3 ® ZnO + CO2, 125.3 g of ZnCO3 ® 81.3 g of ZnO and 22.4 L of CO2 at STP, 2.32 g of ZnCO3 gives ? of ZnO and ? of CO2 at STP, 2.32 × 81.3, 2.32 × 22.4, g of ZnO and, L of CO2 = 1.5 g of ZnO and 0.41 L of CO2., 125.3, 125.3, EXAMPLE, One mole of hydrocarbon is subjected to combustion. The product obtained is condensed and, the resulting gaseous product occupied a volume of 89.6 L at STP. Oxygen required for this, combustion is 145.6 L. at STP. What should be the molecular formula of x?, SOLUTION, y, y, Equation for the combustion of hydrocarbon is CxHy+  x +  O2 ® xCO2 + H2O., , , 2, 4, The gaseous product left after condensation of water vapour is CO2., 89.6 L CO2=, , 89.6, = 4 moles ;, 22.4, , \x=4, 1 mole of O2 occupies 22.4 L of volume at STP, 145.6 ×1, = 6.5 moles of O2, 145.6 L of O2 1 corresponds to =, 22.4, y, y, ∴ x + = 6.5 ; 4 + = 6.5 Þ y = 10 ∴ Hydrocarbon is C4H10., 4, 4, EXAMPLE, 24.58 g of 80% pure potassium chlorate gives certain amount of oxygen which is sufficient for the, combustion of how many grams of acetylene at STP? (Molecular formula of acetylene is C2H2)., SOLUTION, 2KClO3 ® 2KCl + 3O2, 80×24.58, Amount of pure KClO3 in 24.58 g of 80 % sample =, = 19.66 g, 100, 245 g KClO3 gives 96 g O2, 96×19.66, 7.7, = 7.7 g O2 \ No. of moles of O2 =, = 0.24, 245, 32, C2H2 + 5/2O2 ® 2CO2 + H2O, 2.5 moles of oxygen reacts with 1 mole acetylene, 0.24×1, 0.24 moles of oxygen reacts with, = 0.096 moles, 2.5, Amount of acetylene subjected to combustion = 0.096 × 26 =2.504 g, 19.66 g KClO3 gives

Page 23 :
Mole Concept, Stoichiometry and Behaviour of Gases, , EXAMPLE, A mixture of sodium carbonate and sodium bicarbonate was subjected to heating. Some loss in, weight was found. How does this information help us to find out the composition of mixture?, SOLUTION, Between sodium carbonate and sodium bicarbonate, only sodium bicarbonate decomposes to, given sodium carbonate, CO2 and H2O. The gaseous products (CO2 and H2O) escape out into, the atmosphere. Therefore, an apparent loss in weight occurs during the reaction.This loss in, weight corresponds to the amount of gaseous products formed. From the mass of gaseous products, formed, amount of sodium bicarbonate in the mixture can be obtained, and thus, composition of, the mixture can be found out., , EXAMPLE, The percentage of oxygen in a metallic oxide of an alkali metal is 20.1%. The molecular mass of, the compound is 79.5. Write the molecular formula of the compound considering the symbol of, the metal as M and find out the atomic mass of the metal., SOLUTION, The molecular mass of that compound = 79.5, 79.5 × 20.1, The number of oxygen atoms present in one molecule of oxide =, =1, 100 ×16, The metal is univalent since it is alkali metal. The formula could be M2O, The atomic mass of metal be x; 79.5 = 2x + 16 Þ x = 31.75, , 5.23

Page 24 :
5.24, , Chapter 5, , TEST YOUR CONCEPTS, Very Short Answer Type Questions, 1. State Charle’s law., , 13. Ag+1, , Br–1, , 2. State Avogadro’s law., , 14. K+1, , OH–1, , 3. State Graham’s law of diffusion., , 15. NH4+1, , HPO4–2, , 4. 1 mm of Hg = _______ torr., , 16. Ca+2, , HSO4–1, , 5. What is the difference between a Kelvin scale and a, Celsius scale?, , 17. Sn+4, , S–2, , 6. Give the values for the following:, , (i) amount of sodium in 1 mole of sodium, , (ii) amount of nitrogen in 1 mole of nitrogen, 7. Calculate the number of moles present in, , (i) 32 g of sulphur dioxide, , (ii) 34 g of ammonia, 8. Calculate the volume occupied by 0.8 g of methane, at STP., 9. Calculate the molecular weight of, , (i) ammonium sulphate [(NH4)2SO4], , (ii) Cryolite [Na3AlF6], 10. The temperature at which molecular motion ceases, is _____°C or _____ K., , PRACTICE QUESTIONS, , 11. What is STP? Give the values of temperature and, pressure at STP., 12. Pressure of gas molecules is due to _____., Direction for questions from 13 to 17:, In each of the following questions, a positive and, a negative radical is listed. Using the criss-cross, method, write the formula for the compound, that is formed and name the compound., , 18. The SI unit of temperature is _____., Direction for questions from 19 to 24:, Balance the following chemical equations:, 19. NaNO3 → NaNO2 + O2, 20. BeO + NaOH → Na2BeO2 + H2O, 21. LiNO3 → Li2O + NO2 + O2, 22. KI + H2SO4 → K2SO4 + SO2 + I2 + H2O, 23. NaBr + H3PO4 → Na3PO4 + HBr, 24. SO2 + H2S → H2O + S, Direction for questions from 25 to 29:, For each of the following reactions, identify the, products formed and balance the equations:, 25. Na2O2 + H2O →, 26. S + HNO3 →, 27. MnO2 + HCl →, 28. HNO3 + CaCO3 →, 29. Fe2(SO4)3 + NaOH →, 30. Empirical formula of a compound is C2H4O. If its, empirical formula weight is equal to its vapour density,, calculate the molecular formula of the compound., , Short Answer Type Questions, 31. Explain the statement ‘Gases have neither a fixed, shape nor a fixed volume.’, 32. How do gases differ from solids and liquids?, 33. Mention the factors on which the rate of diffusion, of gases depends. Why are similar conditions of, temperature and pressure necessary?, , 34. Calculate the percentage of, , (i) magnesium in magnesium carbonate, , (ii) oxygen in calcium hydroxide, 35. State Gay-Lussac’s law of combining volumes of, gases. Give an example.

Page 25 :
Mole Concept, Stoichiometry and Behaviour of Gases, , 5.25, , 36. 2C2H6 + 7O2 → 4CO2 + 6H2O, , 60 dm3 of ethane is mixed with 448 dm3 of pure, oxygen at STP. If the mixture is ignited and reacts as, illustrated in the above reaction, calculate the volume of CO2 formed., , 41. Two flasks A and B of equal volumes are kept under, similar conditions of temperature and pressure. If, flask A holds 16.2 g of gas X while flask B holds, 1.35 g of hydrogen, calculate the relative molecular, mass of gas X., , 37. The relation between gram molecular mass and, gram molecular volume is established by Avogadro’s, law. Explain., , 42. A gaseous hydrocarbon of vapour density 14 contains 85.2% of carbon. Calculate its molecular, formula., , 38. Calculate the weight of the following gases which, occupy a volume 3.36 dm3 at STP:, , (i) nitrogen, , (ii) hydrogen, , (iii) helium, 39. Calculate the number of moles in, , (i) 29.4 g of H2SO4, , (ii) 31.9 g of hydrated copper sulphate, , (iii) 5 g of CaCO3, , 43. Calculate the amount of mercury obtained by the, decomposition of 2.16 kg of mercuric oxide., , 40. Calculate the weight (in g) of 5 × 1024 molecules of, nitrogen dioxide., , 44. Give the values for the following:, , (a) Gram molecule of helium = __________ g of, helium., , (b) Gram atom of chlorine = __________ g of, chlorine., , (c) Gram atom of potassium = __________ g of, potassium., 45. Calculate the amount of potassium chloride, obtained by the thermal decomposition of 12.25 kg, of potassium chlorate., , Essay Type Questions, 49. Calculate the volume of CO2 formed at STP and, the weight of zinc oxide formed in grams, when, 2.32 g of zinc carbonate decomposes with no, ­further loss in weight., 50. Calculate the volume of CO2 formed at STP and, weight of calcium oxide formed, in grams, when, 5.5 g of calcium carbonate crystals decompose with, no further loss in weight., , CONCEPT APPLICATION, Level 1, Direction for questions from 1 to 7:, State whether the following statements are true, or false., 1. Pressure of a gas is measured using a barometer., 2. Volume of the given mass of a gas is directly, ­proportional to pressure at constant temperature., 3. The number of molecules present in 16 g of s­ ulphur, dioxide is 3 × 1023., , 4. The volume of 32 g of oxygen at STP is 224 L., 5. Under similar conditions of temperature and pressure the ratio of rate of diffusion of methane and, sulphur dioxide is 2 : 1., 6. The vapour density of hydrogen peroxide is equal, to molecular weight of NH3., 7. Real gases obey gas laws under all conditions., , PRACTICE QUESTIONS, , 46. 47 g of impure Al2O3 is reduced electrolytically to, give aluminium and oxygen. Calculate the amount, of aluminium produced., 47. Calculate the empirical and molecular formula of, an organic compound whose percentage composition is C = 70.54%, H = 5.87%, O = 23.52%. The, molecular weight of compound is 136., 48. Calculate the empirical and molecular formula of a, compound whose molecular weight is 120 and has, the following percentage compositions:, , Mg = 19.68%; S = 26.24%, O = 52.48%

Page 26 :
Chapter 5, , 5.26, , 17. Which of the following graphs is true for a given, mass of a gas at constant pressure?, , Direction for questions from 8 to 14:, Fill in the blanks., 8. 9.2 g of sodium contains _____ atoms., , (a), , 9. Marsh gas in coal mines is detected by using ______ law., , (b), VL, , V (mL), , 10. The volume of 5 gram molecules of methane gas is, __________at STP., 11. 1 mole of argon gas contains _____ number of, ­fundamental particles., , t ( °c), T(K), , (c), , 12. The ratio of a gram atomic weight of nitrogen and, oxygen is __________., 13. Empirical formula of a compound is C2H5 and its, molecular weight is 58, then its molecular formula, is _____., 14. The measurable properties of a gas are _____,, _____ and _____., Direction for question 15:, Match the entries given in Column A with, appropriate ones in Column B., , PRACTICE QUESTIONS, , 15., , Column A, A. Avogadro number, B. Percentage weight of oxygen, in Na2O, C. Empirical formula of oxalic, acid, D. Empirical formula of acetic, acid, E. Percentage of carbon in, methane, , Column B, ( ) a. 25.8%, ( ) b. , 75%, ( ) c. 6023 × 1023, ( ) d. CHO2, , V, 0, , (1/P), , 0, , (1/P), , 0, , (1/P), , (d), , V, , V, , , , 0, , (1/P), , V (mL), 0, , t (°c ), , 18. At constant temperature, when the volume of a, gas is reduced to (1/3)rd, the pressure will increase, _______., (a) 1 time, (b) 2 times, (c) 3 times, (d) 4 times, 19. A monovalent positive radical, combines with a, chromate radical. Now, identify the formula of the, compound formed., (a) XCrO4, (b) X2CrO4, (c) X2Cr2O7, (d) X(Cr2O7)2, 20. Which of the following graphs is true for the given, mass of a gas at constant temperature?, (a), , (b), , PV, , ( ) e. CH2O, , 16. Which of the following graphs is true for the given, mass of a gas at constant temperature?, (a), (b), , , (c), , t (°c), , V (mL), , PV, , Direction for questions from 16 to 45:, For each of the questions, four choices have been, provided. Select the correct alternative., , V, , (d), , , (c), , 0, , 0, , P, , P, , (d), PV, , PV, , 0, , P, , 0, , P, , 21. The formula of calcium dihydrogen phosphate is, (a) CaH2PO4, (b) Ca(HPO4)2, (c) Ca(H2PO4)2, (d) Ca3(PO4)2, 22. The number of oxygen atoms present in 0.25 moles, of magnesium perchlorate is, (a) 4N, (b) 8N, (c) 6N, (d) 2N, 23. Vapour density of SO3 is _______., (a) 80, (b) 48, (c) 32, (d) 40

Page 27 :
Mole Concept, Stoichiometry and Behaviour of Gases, , (c) 2 times that of O2, (d) 2 times that of O2, 25. If the rate of diffusion of a gas is r and its density, is d, then under similar conditions of pressure and, temperature _______., (a) r ∝ d, (b) r ∝ d, 1, 1, (d) r ∝, d, d, 26. The volume of CO2 liberated at STP on burning, 24 g of carbon in excess oxygen is _______., (a) 22.4 L, (b) 44.8 L, (c) 16.8 L, (d) 67.2 L, (c) r ∝, , 27. Which among the following contain 43.4% of, sodium?, (a) sodium bicarbonate, (b) sodium nitrate, (c) sodium carbonate, (d) sodium chloride, 28. The number of atoms present in 16 g of O2 is, _______., (a) 6.023 × 1023, (b) 3.011 × 1023, 23, (c) 12.046 × 10, (d) 3.011 × 1022, 29. In which of the following cases, empirical formula, is the same as molecular formula?, (a) sucrose, (b) C6H6, (c) C2H5COOH, (d) glucose, 30. 50 g of magnesium on treatment 40 g of carbon, dioxide gives magnesium oxide. In this amount of, excess reagent taken is, (a) 8.5 g, (b) 6.37 g, (c) 5.5 g, (d) 7.5 g, 31. Identify the correct sequence of relevant steps to, write the formula of cupric bisulphate., , (1) , Writing the symbol of a negative radical as, HSO4–2., , (2) Writing the symbol of a positive radical as Cu+2., , (3) , Writing the symbol of a negative radical as, HSO4–., , , (4) Writing the symbol of a positive radical as Cu+., , (5) Interchanging the valencies of positive and negative radicals and writing subscripts as 1 and 2., , (6) Interchanging the valencies of positive and negative radicals and writing subscripts as 2 and 1., , (7) Keeping HSO4 in parenthesis., , (8) Keeping Cu in parenthesis., (a) 2 1 5 8, (b) 2 3 5 7, (c) 4 3 6 8, (d) 4 1 6 7, 32. Arrange the following relevant points in a proper, sequence to explain why gases exert pressure., , (1) Gas molecules are in random motion., , (2) Kinetic energy of gas molecules is proportional, to absolute temperature., , (3) , A gas is made up of tiny particles called, molecules., , (4) Intermolecular forces of attraction are negligible in gases., , (5) , During random motion, the gas molecules, ­collide with each other., , (6) , During random motion, the gas molecules, ­collide with the walls of a container., (a) 3 1 4 5 6, (b) 3 2 4 6 5, (c) 3 4 1 6, (d) 3 4 1 5 6, 33. Arrange the following relevant points in a proper, sequence for explaining why Kelvin scale is preferred to Celsius scale in the study of gases., , (1) –273°C is the least possible temperature., , (2) A graph of volume vs temperature is a straight, line passing through origin., , (3) A graph of volume vs temperature (°C) is a, straight line which intersects volume axis at, some point., , (4) , Extrapolation of straight line touches the, ­volume axis at –237°C., , (5) –237°C is called absolute zero or 0 K., , (6) All values of temperature are positive in Kelvin, scale., , (7) Usage of negative values for temperature gives, negative values for other properties, like, pressure and volume., (a) 3 4 1 5 6, (b) 2 4 1 5 6, (c) 3 4 6 5 1 7, (d) 2 4 6 5 1 2, 34. The ratio of phosphorus atoms present in calcium, phosphide and magnesium phosphate is, , PRACTICE QUESTIONS, , 24. If equal volumes of two gases, CH4 and O2, are, allowed to diffuse, then the time taken for diffusion, of CH4 is found to be, 1, (a) times that of O2, 2, 1, (b), times that of O2, 2, , 5.27

Page 28 :
5.28, , Chapter 5, , (a) 1 : 2, (c) 1 : 3, , (b) 2 : 1, (d) 1 : 1, , 35. For which of the following reactions, is Gay-Lussac’s, law not applicable?, (a) formation of HI from its constituents, (b) formation of NH3 from its constituents, (c) formation of CO2 from its constituents, (d) formation of SO3 from SO2 and O2, 36. The ratio of number of molecules present in a given, mass of oxygen and sulphur trioxide is, (a) 2 : 1, (b) 5 : 2, (c) 2 : 5, (d) 1 : 2, 37. In which of the following cases, is the empirical, formula same as the molecular formula?, (a) C12H22O11, (b) C6H6, (c) C3H5COOH, (d) C6H12O6, , PRACTICE QUESTIONS, , 38. Which of the following reactions is associated with, same volume ratio as the reaction of formation of, CO2 from CO and O2?, (a) synthesis of ammonia, (b) synthesis of HCl, (c) formation of SO3 from SO2 and O2, (d) synthesis of nitric oxide, 39. At constant temperature, a gas is at a pressure of 940, mm of Hg. At what pressure, its volume decreases, by 40%?, (a) 564 mm of Hg, (b) 1860 mm of Hg, (c) 2350 mm of Hg, (d) 1567 mm of Hg, 40. The number of molecules present in 2.8 g of nitrogen is, (a) 6.023 × 1023, (b) 6.023 × 1022, (c) 6.023 × 1021, (d) 6.023 × 1020, , 41. If the formula of a metallic nitrate is M(NO3)2,, then what will be the formula of the nitride of that, metal?, (a) MN2, (b) M3N2, (c) M2N, (d) M2N3, 42. The ratio of rates of diffusion of two gases X and Y, is 4 : 11 . If the molecular mass of Y is double to, the molecular mass of oxygen, then X is, (a) CO, (b) SO3, (c) CO2, (d) NO, 43. 160 mL of carbon monoxide is mixed with 100 mL, of oxygen and the mixture is ignited. What volume, of oxygen is left behind? (Assume that all volumes, are measured under same conditions.), (a) 80 mL, (b) 60 mL, (c) 20 mL, (d) 40 mL, 44. Assertion (A): One gram molecule of any gas, occupies 22.4 L volume at STP, , Reason (R): Under similar conditions of temperature and pressure equal masses of all gases occupy, equal volumes., (a) Both A and R are correct and R is the correct, explanation for A, (b) Both A and R are correct but R is not the correct explanation for A, (c) A is correct, but R is wrong, (d) A is wrong, but R is correct, 45. What is the volume of oxygen liberated at STP, when 24.5 g of potassium chlorate is subjected to, heating?, (a) 3.36 L, (b) 5.6 L, (c) 6.72 L, (d) 16.8 L, , Level 2, 1. Why is temperature in Kelvin scale always positive?, Also explain why Kelvin temperature is used only, in studying gas laws., 2. A certain amount of a gas is filled in a tank of volume 63000 L and 42 atm. If this gas is transferred, to a cylinder of volume of 1260 L, find the number, of cylinders that can be filled with the given gas at, STP? (assume complete evacuation of the cylinder), , 3. One mole of hydrocarbon is subjected to combustion. The product obtained is condensed and the, resulting gaseous product occupied a volume of, 89.6 L at STP. Oxygen required for this combustion is 145.6 L at STP. What should be the molecular formula of x?, 4. How many molecules of hydrogen chloride can be, synthesised from 896 L of chlorine gas at STP?

Page 29 :
Mole Concept, Stoichiometry and Behaviour of Gases, , 6. The ratio of nitrogen and oxygen by mass present, in a colourless gas is 7 : 8. When this colourless, gas combines with O2, it produces 44800 cm3 of, a brown-coloured gas at STP. Find out the number of moles of oxygen that have taken part in the, reaction., 7. In an organic compound the percentage of carbon, and hydrogen are 40 and 6.7, respectively. If the, vapour density of the compound is 30, what is the, molecular formula of the compound?, 8. How many grams of oxygen contain the same, number of molecules as present in 352 g of CO2?, 9. The volume occupied by oxygen at STP obtained, on heating the 490 g of KClO3 is 130 L. Calculate, the percentage purity of KClO3 [KClO3 on heating, produces KCl and O2]., 10. Balance the following chemical reactions by identifying the products:, (a) CuSO4 + HI → CuI2 ___, (b) PCl5 + H2O → H3PO4 + ____, (c) Fe3O4 + HCl → FeCl2 + FeCl3 _____, (d) Al2O3 + N2 + C → AlN + ____, 11. How many moles of water are required to be dissociated to produce oxygen which is just sufficient, to form 800 g of magnesium oxide by burning, ­magnesium? (atomic weight of Mg is 24), 12. The mass of 256 mL of a triatomic elemental gas at, 27°C and 4 atm is 2 g. Calculate the weight of one, atom., 13. 710 g of chlorine gas contains X atoms of chlorine., Calculate the mass of sodium chloride which contains X number of chloride radicals. (atomic weight, of Na is 23 g), 14. Two gases A and B, which do not chemically react,, are taken in two 1 L containers. They are found to, exert pressures P1 and P2, respectively. When the, mixture of the gases A and B is taken in another, 1 L container, the pressure exerted is found to be, (P1 + P2). How can you justify this on the basis of, kinetic molecular theory?, , 15. A particular compound contains only nitrogen and, hydrogen. The percentage of nitrogen in that compound is 875%. Further, 96 g of that compound, contains 18 × 1023 molecules of that substance., Find out the molecular formula of that compound., Directions for questions from 16 to 25:, Application-Based Questions, 16. The ratio of non-metal atoms to the number of, atoms of two non-metallic oxides A and B are 0.33, and 0.25, respectively. Find the valencies of nonmetals present in those non-metallic oxides., 17. Two moles of chlorine atoms are present in how, many grams of chlorine gas?, 18. A cylinder is filled with a mixture of equal number of molecules of oxygen, carbon dioxide and, helium. When leakage occurs, do equal amounts of, gases come out? Give a reason., 19. At what centigrade temperature, will the volume of, a given mass of a gas at 0°C triple itself if pressure is, kept constant?, 20. Two gases A and B are kept in two cylinders and, allowed to diffuse through a small hole. If the time, taken by gas A is four times the time taken by gas, B for diffusion of equal volume of gas under similar, conditions of temperature and pressure, what will, be the ratio of their molecular masses?, 21. If the volume occupied by a certain mass of gas is, decreased by 60%, what would be the percentage, change in pressure at the same temperature?, 22. The percentage of a trivalent metal in a metallic, oxide is 53%. How many grams of this metallic, oxide should be required to produce 22.8 g of salt, when treated with excess sulphuric acid?, 23. 448 L of ammonia at STP on decomposition gives, X g of nitrogen. How many molecules of oxygen, are required to produce NO2 from X g of nitrogen?, 24. Calculate the number of molecules of gaseous product obtained on heating 8.8 g of CO2 with coke if, the conversion of CO2 is 80% by mass., 25. The volume occupied by oxygen at STP obtained, on heating the 490 g of KClO3 is 130 L. Calculate, the percentage purity of KClO3 [KClO3 on heating, produces KCl and O2]., , PRACTICE QUESTIONS, , 5. How many grams of magnesium nitrate should be, heated to produce oxygen which is just sufficient to, form 15.3 g of alumina?, , 5.29

Page 30 :
5.30, , Chapter 5, , Level 3, 1. There are four different metal halides—A, B, C and, D. The ratio of the number of constituent atoms, (i.e., metal and halogen atoms present) in one gram, molecule of those metal halides are 1, 05, 025 and, 033, respectively. Find the valency of the metals, present in those metal halides. Give reasons in support of your answer., 2. 500 mL of a monoatomic gas X diffuses through, a hole at a pressure of 4 atm and 127. 1500 mL of, another elemental diatomic gas Y diffuses through, the same hole at a pressure of 2 atm and 27°C. If, the time taken for both the diffusion processes is the, same, then compare the atomic weights of the two, gases., 3. Under what conditions can ideal gases be liquefied?, Give reasons to support your answer., 4. The molecular weight of gas A is 10 times greater, than the molecular weight of gas B. These two gases, are taken in cylinders of 5 L volume at 1 atm pressure and 27°C. Comment on the number of molecules in the two gases. Justify with respect to kinetic, molecular theory of gases., , PRACTICE QUESTIONS, , 5. Easily liquefiable gases show larger deviations from, gas laws. Comment on this statement on the basis, of kinetic molecular theory., Directions for questions from 6 to 10:, Application-Based Questions, 6. A certain volume of O2 gas is kept in a cylinder fitted with a movable piston. If all the O2 molecules, present in that cylinder get converted to O3 molecules at the same temperature and pressure, will, , you observe any change in the system? Calculate, the percentage change if any change takes place., Justify your answer with appropriate reasons., 7. Equal volumes of CO and O2 are kept in a closed, cylinder under certain temperature and pressure., The mixture is heated till all the CO gets converted to CO2. Then, the temperature of the gases, is brought to the previous temperature. Will there, be any change in any parameter of the gas or gases, present in the cylinder? Justify your answer with, appropriate reasons. If any change takes place, calculate the percentage change., 8. A sample of a mixture of Na2CO3 and NaHCO3, is subjected to heating till there is no further loss, in weight. Assuming that the loss in weight of the, sample is 22% of the initial weight of the mixture, due to the evolution of CO2, find out the relative, percentages of the two components in the mixture., 9. A patient Vasu, had to survive for a month on artificial respiration before he passed away. A nurse was, instructed to give him 7.5 g of glucose per hour, for consumption to meet the energy requirement., What volume of carbogen (95% O2 + 5% CO2), had to be supplied for Vasu assuming that he was, kept under the conditions of 27°C and normal, atmospheric pressure?, 10. 64.5% pure sample of zinc when treated with excess, of dil HCl liberated some volume of hydrogen gas, at STP. This hydrogen is utilised for the reduction of, 23.2 g Fe3O4. Find out the amount of iron obtained, and also amount of impure zinc taken. [atomic mass, of Zn = 65.5 and Fe = 56].

Page 31 :
Mole Concept, Stoichiometry and Behaviour of Gases, , 5.31, , CONCEPT APPLICATION, Level 1, True or false, 1. True, , 2. False, , 3. False, , 5. True, , 6. True, , 7. False, , 4. True, , Fill in the blanks, 8. 2.4 × 1023, 12. 7 : 8, , 9. Grahams, , 10. 112 L, , 13. C4H10, , 11. 54 N, , 14. Pressure, volume,, temperature, , Match the following, 15. A : c, , B:a, , C:d, , D:e, , E:b, , 16. a, , 20. b, , 24. b, , 28. a, , 17. c, , 21. c, , 25. c, , 29. a, , 18. c, , 22. d, , 26. b, , 30. b, , 19. b, , 23. d, , 27. c, , 31. (i) writing the symbol of positive radical as Cu+2, , (ii) writing the symbol of negative radical as HSO–4, , (iii) Interchanging the valencies of positive and negative radicals and writing 1 and 2 as subscripts., , (iv) keeping HSO4 in parenthesis, 32. (i) Gas is made up of tiny particles called molecules., , (ii) Intermolecular forces of attraction are negligible, in gases., , (iii) Gas molecules are in random motion., , (iv) , During random motion, the gas molecules, collide with the walls of the container., 33. (i) , A graph of volume vs temperature (°C) is a, straight line which intersects volume axis at, some point., , (ii) , Extrapolation of straight line touches the, volume axis at –273°C., , , (iii) –273 °C is the least possible temperature., , (iv) –273°C is called absolute zero or 0 Kelvin., , (v) All values of temperature are positive in Kelvin, scale., , (vi) Usage of negative values gives negative values for, other properties, like, pressure and volume., 34. Ca3P2, Mg3(PO4)2, , 3 Ca atoms, 3 Mg atoms, , 2 P atoms, 2 P atoms, , 8 O atoms, , The ratio of phosphorus atoms is 2 : 2 = 1 : 1, 35. Constituents of CO2 are carbon and oxygen where, carbon is a solid, Gay-Lussac’s law is applicable for, only gaseous reactions., 36. 32 g of oxygen contains N molecules, 80, 32 g of SO3 contains, N molecules, 32, , H I N T S A N D E X P L A N AT I O N, , Multiple choice questions

Page 32 :
5.32, , Chapter 5, , , Ratio of number of molecules present in 32 g, 80, , of O2 and SO3 = N : N = 2.5 : 1 = 5 : 2, 32, 37. C12H22O11, empirical and molecular formulaes are, same, 38. 2CO + O2 → 2CO2. The volume ratio is 2 : 1 : 2., , 2 vol : 1 vol : 2 vol, , Formation of SO3 can be represented as 2SO2 + O2, → 2SO3 also possesses same volume ratio (2 : 1 : 2), 39. P1 = 940 mm of Hg, V2 = 60 L, , V1 = 100 L, P2 = ?, PV, 940 × 100, P2 = 1 1 =, = 1567 mm of Hg, V2, 60, , 4, =, 11, , 64, 16 64, ⇒, =, ⇒ M x = 44, Mx, 11 M x, , , ∴ Gas X is CO2, 43. 2CO + O2 → 2CO2, , 2 moles of CO react with 1 mole of O2, , 160 mL (moles) of CO react with ? mL (moles) of, O2, 160 × 1, = 80 ml of O2, 2, , ∴ Volume of O2 left = 100 – 80 = 20 mL, =, , 44. One gram molecule of any gas occupies 22.4 L, ­volume at STP., , 40. 28 g of nitrogen contains 6.023 × 1023 molecules, , 2.8 g of nitrogen contains 6.023 × 1022 molecules, , , According to Avogadro’s law, under similar conditions of temperature and pressure equal moles but, not equal mass of all gases occupy equal volumes., , 41. M(NO3)2 ⇒ Valency of M is +2, , ∆, 45. 2KClO3 , → 2KCl + 3O2 ↑, , , Metal nitride M+2 N–3 ⇒ M3N2, , , 2 moles of KClO3 → 3 moles of O2, , r, 4, 42. x =, =, ry, 11, , My, , 4, ⇒, =, Mx, 11, , My, Mx, , (1), , , Molecular weight of O2 = 32, , H I N T S A N D E X P L A N AT I O N, , ∴, , , ∴ Molecular weight of Y = 2 × 32 = 64, , 24.5, 3 × 0.2, = 0.2 moles → x =, 122.5, 2, , = 0.3 moles of O2, , 1 mole → 22.4 L, , 0.3 → x = 6.72 L, , Level 2, 1. (i) Charles’ law, , ( ii) determination of Kelvin from Charles law, , (iii) , relation between change in volume with, temperature, 2. (i), , (ii), , (iii), , (iv), , Boyle’s law, volume of gas at STP, determination of number of cylinders, 2100 cylinders, , 3. (i) , balanced equation for combustion of, hydrocarbon, , (ii) identification of the product that is condensed, , (iii) calculation of number of moles of the gaseous, product and oxygen from the given volume, , (iv) determination of the molecular formula of the, hydrocarbon, (v) C4H10, , 4. (i) relation between volume of the gas at STP and, number of moles, , (ii) 48 × 1023 molecules, 5. (i) Calculation of amount of oxygen required for, the formation of given amount of alumina., , (ii) Balanced chemical equation for the decomposition of magnesium nitrate., , (iii) , Calculation of mass of magnesium nitrate, required to be heated., , (iv) 66.6 g, 6. (i) Identification of the colourless gas., , (ii) Balanced chemical equation of combustion of, colourless gas., , (iii) , Relate volume of products to number of, moles of oxygen consumed., , (iv) 1 mole

Page 33 :
Mole Concept, Stoichiometry and Behaviour of Gases, , 8. (i) Relation between the mass and the number of, molecules., , (ii) Number of moles of CO2., , (iii) Mass of O2 containing equal number of moles, as CO2., , (iv) 256 g, 9. (i) weight–volume relationship, , (ii) Balanced chemical equation of decomposition, of KClO3., , (iii) Relating volume of O2 obtained and mass of, KClO3 actually present., , (iv) calculation of percentage purity, (v) 96.7%, 10. (i) type of chemical reaction, , (ii) balancing by keeping appropriate coefficients, 11. (i) relationship between the mass of reactants and, products, , (ii) , balanced chemical equation for synthesis of, MgO, , (iii) relating number of moles of oxygen and, amount of MgO, , (iv) , balanced chemical equation for dissociation of, water, (v) relating number of moles of oxygen and water, , (vi) 20 moles, , 14. Relation between the number of molecules of a gas, and its pressure, 15. (i) , relation between the number of molecules, and the gram molecular weight of a substance, , (ii) finding molecular weight relating given mass, and number of molecules, , (iii) percentage of hydrogen, , (iv) empirical formula of compound, (v) , relating empirical formula and molecular, weight to derive molecular formula, , (vi) N2H4, 16. Let the non-metallic oxide be XxOy., x, = 0.33 ⇒ x = x(0.33) + y(0.33), ∴, x+y, , ⇒ 0.67x = 0.33y ⇒ x:y = 1:2, , Hence, the number of oxygen atoms is 2, as the, valency of oxygen is’ two, the valency of the nonmetal is four., , Let the non-metallic oxide be Xx Oy., , In B, ∴, , x, = 0.25 ⇒ x = 0.25x + 0.25y, x+y, , , ⇒ 0.75x = 0.25y, , ⇒ x:y = 1:3, , Valency of non-metal, valency of O × No. of O atoms 2 × 3, =, =, =6, Number of non-metal atoms, 1, 17. 1 molecule of chlorine gas consists of two chlorine, atoms. Hence, 2 atoms of chlorine are present in 1, molecule of chlorine gas that is 71 g of Cl2., 18. When leakage occurs in a cylinder containing a, gaseous mixture containing equal masses of different gases, equal amounts of gases do not come out., This is because rate of diffusion of a gas depends on, its molecular mass. The order of molecular masses, of the gases is He < O2 < CO2. The rate of diffusion is in the order He > O2 > CO2., , 12. (i) ideal gas equation, , (ii) calculation of the volume occupied by the gas, at STP, , (iii) calculation of the molecular weight of the gas, from the mass given, , (iv) relation between gram molecular weight and, number of molecules, (v) calculation of the weight of one atom, , (vi) 2.66 × 1023, , , From the mixture, maximum amount of helium, comes out, whereas minimum amount of CO2, comes out., , 13. (i) Calculation of X from the given mass., , (ii) relation between gram atomic weight, given, mass and number of atoms, , (iii) 1170 g, , 19. 0°C corresponds to 273 K. Since volume of a gas, is directly proportional to absolute temperature at, constant pressure, the volume gets tripled when, temperature is tripled., , H I N T S A N D E X P L A N AT I O N, , 7. (i) Calculation of atomic ratio from the percentages of various elements., , (ii) Determination of empirical formula., , (iii) , Relation between molecular weight and, vapour density., , (iv) Determination of molecular formula., (v) C2H4O2, , 5.33

Page 34 :
Chapter 5, , 5.34, , , T1 = 273 K, T2 = ?,, ,  2x , 100 = 53 ⇒ x = 27.06, ∴,  2x + 48 , , , V1 = V, V2 = 3V,, V1 V2, VT, 3V × 273, =, ⇒ T2 = 2 1 =, = 819 K, T1 T2, V1, V, , t = 819 – 273 = 546°C, , , ? ← 22.8 g of Al2(SO4)3, , Volume of gas diffused (v ), time taken (t ), , =, , , Let time taken by gas B be t., , 22.8 × 102, = 6.87 g., 342, , , Then, rate of diffusion of, , 23. 2NH3 → N2 + 3H2, , Volume of gas B diffused (V1 ), B=, t, , according to the given data, , , 2(22.4) L of NH3 → 22.4 L of N2, , , time taken by gas A = 4 × time taken by gas B, =4×t, , , , A=, , Volume gas A diffused (V2 ), 4×t, , , ∴ V1 = V2, , , N2 + 2O2 → 2NO2, , rate of diffusion of A rA V1 t, = = ×, =, rate of diffusion of B rB 4t V2, rA 1, = =, rB 4, , MB, MA, , MB, MA, , 1 M, , Squaring on both sides = = B, 6 MA, , MA : MB = 16 : 1, 21. P1 = P, V1 = V, V2 = V −, , 28 × 224, = 280 g, 22.4, ∴ X = 280 g, =, , , Volume of gas B diffused = Volume of gas A diffused, , ∴, , , 448 L → ?, 448 × 22.4, =, = 224 L, 2 × 22.4, , 28 g of N2 corresponds to 22.4 L, , ? corresponds to 224 L, , , ∴ rate of diffusion of, , H I N T S A N D E X P L A N AT I O N, , , Al2O3 + 3H2SO4 → Al2(SO4)3 + 3H2O, , (54 + 48) g of Al2O3 gives [54 + 3(96)]g of, Al2(SO4)3, , 20. rate of diffusion(effusion), =, , , ∴ The metal is Al and formula of oxide is Al2O3., , 60V, 100, , , P2 = ?, PV, PV, = 2.5P, 1 1 = P2V 2 , P2 =, 60V, V−, 100, (2.5P − P ), , Percentage change =, × 100 = 150%, P, 22. The formula of metal oxide is M2O3., , Let the atomic weight of metal be x., , , 28 g of N2 → 64 g of O2, , 280 g → ?, 280 × 64, =, = 640 g, 28, , 32 g → 6 × 1023 molecules, , 640 g → ?, =, , 640 × 6 × 1023, = 12 × 1024 molecules, 32, , 24. CO2 + C → 2CO, , 44 g of CO2 → 2 × 6 × 1023 molecules of CO, , 8.88 g of CO2 → ?, 8.8 × 12 × 1023, = 24 × 1023 molecules, 44, , 100% conversion → 2.4 × 1023 molecules, =, , , 80% conversion → ?, =, , 80 × 2.4 × 1023, = 1.92 × 1023 molecules, 100

Page 35 :
Mole Concept, Stoichiometry and Behaviour of Gases, , 25. 2 KClO3 → 2 KCl + 3O2, , 2 × 122.5 g of KClO3 → 3 × 22.4 L of O2 at STP, , ? → 130 L of O2 at STP, , =, , 5.35, , 2 × 122.5 × 130, = 473 g of KCIO3, 3 × 22.4, , , % of purity of KCIO3 =, , 473, × 100 = 96.7%, 490, , Level 3, 1. (i) Relation between the number of constituent, atoms present in 1 molecule of the substance, and their valency., , (ii) Number of metal and halogen atoms in A, B,, C and D., , (iii) , Valency of metal depending on number of, ­halogens the metal is associated with., , , (ii) Properties of gas based on kinetic molecular, theory which follow gas laws., , (iii) Property which makes gases easily liquefiable., , (iv) Comparison of properties of easily liquefiable, gases and ideal gases., , , (iv), , , , , , ∴ The volume will be reduced if the temperature, and pressure are kept constant., , 2. (i) ideal gas equation, , (ii) Comparison of the volumes of gases X and Y, under similar conditions of temperature and, pressure., , (iii) Calculation of the ratio of rate of diffusion of, X and Y., , (iv) Determination of the ratio of their molecular, weights., , (v) , Comparison of atomic weights from the, atomicity of the gases., , (vi) (At wt)y × 8 = (At wt)x, 3. (i), , (ii), , (iii), , (iv), , properties of ideal gases, conditions for liquefaction of any gas, applying these conditions to ideal gases, unique nature of ideal gas, , 4. (i) the cause of pressure for the gas, , (ii) Relation between the number of molecules, and pressure exerted by the gas provided the, volume is kept fixed., , (iii) , Comparison of the number of molecules, of the gases under the given condition of, temperature., 5. (i) Comparing properties of gas which follow gas, laws and easily liquefiable gases., , , 3 moles of O2 are converted to 2 moles of O3., , , Let the volume of O2 be x L., , ∴ The volume of O3 will be, , 2x, L, 3, , , ∴ Percentage reduction of volume =, , 2x, 3 × 100, x, , x−, , x, x, = 3 × 100 =, × 100 = 33.33%, x, 3x, 7. 2CO + O2 → 2CO2, , Temperature is brought down to the previous temperature and the volume of the cylinder is fixed., , ∴ Pressure will be reduced, because the number of, molecules will be reduced., , Let 2n molecules of CO and 2n molecules of O2, be there in that cylinder (an equal volume of any, gas contains the same number of molecules under, similar conditions of temperature and pressure)., , 2n molecules of CO combine with n molecules of, O2 and form 2n molecules of CO2, according to, stoichiometric equation., , After the reaction 2n molecules of CO2 are formed, and n molecules of O2 will be left over. If T and V, are fixed, then pressure is directly proportional to, the number of molecules., , H I N T S A N D E X P L A N AT I O N, , A:1, B:2, C:4, D:3, , 6. 3O2 → 2O3

Page 36 :
Chapter 5, , 5.36, , , ∴, , p1 4 x, =, p 2 3x, , 3p, , ∴ p2 = 1, 4, , Percentage change is equal to, =, , 4 x − 3x, × 100 = 25%, 4x, , 8. 2NaHCO3 → Na2CO3 + H2O + CO2, , Let 100 g be the weight of mixture amount of CO2, produced = 22, , Number of moles CO2 = 0.5, , Amount of NaHCO3 present in the mixture 2, × 0.5 × 84 = 84 g, , Amount of Na2CO3 present in the mixture = 16 g, , % of NaHCO3 = 84%, , % of Na2CO3 = 16%, , H I N T S A N D E X P L A N AT I O N, , 9. C6 H12O6 + 6O2 → 6CO2 + 6H2 O, , Amount of glucose required for 30 days = 7.5 × 24, × 30 = 5400 g, 5400, , ∴ No of moles of glucose =, = 30, 180, , Volume of O2 required for combustion at STP =, 22.4 × 6 × 30 = 4032 L, , STP, , Given conditions, , , T1 = 273 K, , T2 = 300 K, , , P1 = 1atm, , P2 = 1 atm, , , V1 = 4032 L, , V2 = ?, PV, PV, 1 1, = 2 2, T1, T2, , 1 × 4032 × 300, = 4430.76 L, 273 × 1, , ∴ oxygen required = 4430.76 L, ∴ V2 =, , , 95 L of oxygen is present in 100 L of carbogen, 100 × 4430.76, , ∴ 4430 76 L of O2 is present in =, 95, , = 4663.95 L of carbogen, 10. Zn + 2 HCl → ZnCl2 + H2, , Fe3O4 + 4H2 → 3Fe + 4H2O, , Number of moles of Fe3O4 =, , 23.2, = 0.1, 232, , 23. 2 g of Fe3O4 = 0.1 mole, , 1 mole of Fe3O4 requires 4 moles of H2, , 0.1 mole of Fe3O4 requires 0.4 mole of H2, , To evolve 0.4 moles of H2, 0.4 moles of Zn are, required., , Mass of 0.4 mole of Zn = 0.4 × 65.5 = 26.2 g, 26.2 × 100, = 40 g, 65.5, , Amount of iron formed = 0.3 mole = 0.3 × 56, = 16.8 g, , Amount of 64.5% Zn =