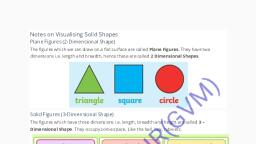
Page 1 :
Class 8 Maths Chapter 15 Mensuration By, Ashutosh sir(GVM), Exercise 15.1, , 1. The length and breadth of a rectangular field are in the ratio 9 : 5. If the, area of the field is 14580 square metres, find the cost of surrounding the, field with a fence at the rate of ₹3.25 per metre., Solution:, , Let the length of rectangle be 9x and its breadth be 5x, So,, Area = l × b, ⇒ 14580 = 9x × 5x, 45x2 = 14580, x2 = 14580/45 = 324, x = √324, x = 18, Hence,, Length = 9 × 18 = 162 m and Breadth = 5 × 18 = 90 m, Now, Perimeter = 2(l + b), = 2 (162 + 90) = 2(252), = 504 m., Therefore, cost for fencing the surrounding 504 m at the rate of ₹3.25 per metre = ₹(504, × 3.25) = ₹1638, , 2. A rectangle is 16 m by 9 m. Find a side of the square whose area equals, the area of the rectangle. By how much does the perimeter of the rectangle, exceed the perimeter of the square?, Solution:, , Area of rectangle = (16 × 9) m2 = 144 m2
Page 2 :
Given condition,, Area of square = Area of rectangle, ∴ (Side)2 = 144, Side = √144 = 12 m, Now,, Perimeter of square = 4 × side = 4 × 12 = 48 m, Perimeter of rectangle = 2(l + b) = 2 (16 + 9) = 50 m, Hence, difference in their perimeters = 50 – 48 = 2 m, ., , 3. Two adjacent sides of a parallelogram are 24 cm and 18 cm. If the, distance between longer sides is 12 cm, find the distance between shorter, sides., Solution:, , Let take 24 cm as the base of parallelogram, then its height is 12 cm., We know that,, Area of parallelogram = base × height, = 24 × 12 = 288 cm2, Let’s consider d cm to be the distance between the shortest sides., ∴ Area of parallelogram = (18 × d) cm2, 18 × d = 288, ⇒ d = 288/18 = 16 cm, Therefore, the distance between the shorter sides is 16 cm.
Page 3 :
4. Rajesh has a square plot with the measurement as shown in the given, figure. He wants to construct a house in the middle of the plot. A garden is, developed around the house. Find the total cost of developing a garden, around the house at the rate of ₹50 per m2., , Solution:, Given,, Side of square plot = 24 m, Length of house (l) = 18 m, and breadth (b) = 12m, Now,, Area of square plot = (24)2 m2 = (24 × 24) m2 = 576 m2, And,, Area of house = 18 × 12 = 216 m2, Remaining area of the garden = 576 m2 – 216 m2 = 360 m2, The cost of developing the garden = ₹50 per m2, Therefore, the total cost = ₹50 × 360 = ₹18000, , 5. A flooring tile has a shape of a parallelogram whose base is 18 cm and the, corresponding height is 6 cm. How many such tiles are required to cover a, floor of area 540 m2? (If required you can split the tiles in whatever way you
Page 4 :
want to fill up the comers)., Solution:, , Given,, , Base of the parallelogram-shaped flooring tile =, 18 cm and its height = 6 cm, So,, Area of one tile = Base × Height, = 18 × 6, = 108 cm2, We have the area of floor = 540 m2, Hence, number of tiles = Total area/ Area of one tile, = (540 x 100 x 100)/108 [As, 1 m2 = (100 x 100) cm2], = 50000, , 6. An ant is moving around a few food pieces of different shapes scattered, on the floor. For which food piece would the ant have to take a longer round?
Page 5 :
Solution:, , (a) Diameter of semicircle = 2.8 cm, ∴ Perimeter = πr + 2r, = 22/7 × 2.8 + 2 × 2.8, = 8.8 + 5.6 cm, = 14.4 cm, (b) Total perimeter = 1.5 + 1.5 + 2.8 + semi circumference (πr, where r = 2.8/2 = 1.4 cm), = 1.5 + 1.5 + 2.8 + (22/7 x 1.4), = 5.8 + 8.8, = 14.6 cm, (c) Total perimeter = 2 + 2 + Semi circumference (πr, where r = 2.8/2 = 1.4 cm), = 4 + 8.8, = 12.8 cm, Hence, it is clearly seen that distance of (b) i.e. 14.6 is the longest.
Page 6 :
7. In the adjoining figure, the area enclosed between the concentric circles is, 770 cm2. If the radius of the outer circle is 21 cm, calculate the radius of the, inner circle., , Solution:, , Given,, Radius of outer circle (R) = 21 cm., Radius of inner circle (r) = r cm., Area of shaded portion = 770 cm2, ⇒ π (R2 – r2) = 770, (212 – r2) = 770, 441 – r2 = 770 × (7/22) = 35 × 7 = 245, r2 = 441 – 245, r2 = 196, r = √196, ∴ r = 14 cm, , 8. A copper wire when bent in the form of a square encloses an area of 121, cm2. If the same wire is bent into the form of a circle, find the area of the
Page 7 :
circle., Solution:, , Given,, Area of the square = 121 cm2, So, side = √121 = 11 cm, Now,, Perimeter = 4 a = 4 × 11= 44 cm, And, circumference of the circle = 44 cm, ∴ Radius = (44 x 7)/ (2 x 22) = 7cm, Therefore, area of the circle = πr2 = (7)2, = 22/7 × 7 × 7, , = 154 cm2, , 9. A rectangular garden 80 m by 40 m is divided into four equal parts by two, cross-paths 2.5 m wide. Find, (i) the area of the cross-paths., (ii) the area of the unshaded portion.
Page 8 :
Solution:, , Given,, Length of rectangular garden = 80 m, and breadth = 40 m, Width of crossing path 2.5 m, So,, Area of length wise path = 80 × 2.5 = 200 m2, and, Area of breadth wise path = 40 × 2.5 = 100 m2, (i) Total area of both paths, = 200 + 100 – 2.5 × 2.5 m2, = 300 – 6.25 = 293.75 m2, (ii) Area of unshaded portion, = Area of garden – Area of paths, = 80 × 40 – 293.75 m2, = 3200 – 293.75 m2
Page 9 :
= 2906.25 m2, , 10. In the given figure, ABCD is a rectangle. Find the area of the shaded, region., , Solution:, , In the given figure, we have, Length of rectangle = 18 cm and breadth = 12 cm, ∴ Area = l × b = 18 × 12 cm2 = 216 cm2, Area of triangle I = ½ × 12 × 10 = 60 cm2, Area of triangle III = ½ × 18 × 7 = 63 cm2
Page 10 :
Thus,, Area of shaded portion, = Area of rectangle – Area of 3 triangles, = 216 – (60 + 63 + 20), = 216 – 143 cm2, = 73 cm2, , Exercise 15.2, , 1. Each sides of a rhombus is 13 cm and one diagonal is 10 cm. Find, (i) the length of its other diagonal, (ii) the area of the rhombus, Solution:, , (i) Given,, Side of rhombus = 13 cm., Length of diagonal AC = 10 cm., ∴ OC = 5 cm., Since, the diagonals of rhombus bisect each other at right angles, So, ∆BOC is rt. angled., Then, by Pythagoras Theorem we have, BC2 = OC2 + OB2, 132 = 52 + OB2, OB2 = 169 – 25 = 144, ⇒ OB = √144 = 12 cm, Hence,, Diagonal BD = 2 × OB = 2 × 12 = 24 cm
Page 11 :
(ii) Area of rhombus = ½ × d1 × d2, = ½ × 10 × 24 = 120cm2, , 2. The cross-section ABCD of a swimming pool is a trapezium. Its width AB =, 14 m, depth at the shallow end is 1-5 m and at the deep end is 8 m. Find the, area of the cross-section., , Solution:, , Here, AD and BC are the two parallel sides of trapezium, And, distance between them is 14 m., ∴ Area of trapezium = ½ (1·5 + 8) × 14, = ½ × 9·5 × 14, = 66.5 m2, , 3. The area of a trapezium is 360 m2, the distance between two parallel sides, is 20 m and one of the parallel side is 25 m. Find the other parallel side., Solution:
Page 12 :
Given,, Area of a trapezium = 360 m2, Distance between two parallel lines = 20 m, One parallel side = 25 m, Now,, Let’s assume the second parallel side to be x m, So, Area = (25 + x) × 20, ⇒ 360 = (25 + x) × 20, ∴ x = 36 – 25 = 11 m, Therefore, the second parallel side is 11 m., , 4. Find the area of a rhombus whose side is 6.5 cm and altitude is 5 cm. If, one of its diagonal is 13 cm long, find the length of other diagonal., Solution:, , Given,, Side of rhombus = 6.5 cm, And altitude = 5 cm, So,, Area of a rhombus = Side × Altitude = 6.5 × 5 = 32.5 cm2
Page 13 :
We have, one diagonal = 13 cm, Hence,, Length of other diagonal = (2 x Area)/ One diagonal, = (32.5 x 2)/ 13, = 5 cm, , 5. From the given diagram, calculate, (i) the area of trapezium ACDE, (ii) the area of parallelogram ABDE, (iii) the area of triangle BCD., , Solution:, (i) Area of trapezium ACDE = ½ × (AC + DE) × h, = ½ × (13 + 7) × 6.5, = ½ × 20 × 6.5, = 65 m2, (ii) Area of parallelogram ABDE = ½ × b × h, = ½ × 6 × 6.5, = 15.5 m2, (iii) Area of ∆BCD = ½ × base × height, = ½ × BC × height, = ½ × 6 × 6.5 [∵ BC = AC – AB = 13 – 7 = 6 m], = 19.5 m2
Page 14 :
6. The area of a rhombus is equal to the area of a triangle whose base and, the corresponding altitude are 24.8 cm and 16.5 cm respectively. If one of, the diagonals of the rhombus is 22 cm, find the length of the other diagonal., Solution:, , Given,, Base of triangle = 24.8 cm and altitude = 16.5 cm, Area = ½ × base × altitude, = ½ × 24.8 × 16.5 cm2, = 204.6 cm2, Now, Area of ∆ = Area of rhombus, But, area of rhombus = 204.6 cm2, Length of one diagonal = 22 cm, Area of rhombus = (First diagonal × Second diagonal), Thus,, Second diagonal = (2 × Area)/ First diagonal, = (204.6 × 2)/ 22, = 18.6 cm, , 7. The perimeter of a trapezium is 52 cm. If its non-parallel sides are 10 cm, each and its altitude is 8 cm, find the area of the trapezium., Solution:
Page 15 :
Given,, Perimeter of a trapezium = 52 cm, Length of each non-parallel side = 10 cm, Altitude DL = 8 cm, Now,, In right ∆DAL, by Pythagoras Theorem we have, DA2 = DL2 + AL2, (10)2 = (8)2 + AL2, 100 = 64 + AL2, AL2 = 100 – 64 = 36 = (6)2, ∴ AL = 6 cm, Similarly,, BM = 6 cm and DC = LM, Also, we have, Perimeter = AB + BC + CD + DA, and CD = DA, So, CD + DA = 2DA, But,, AB + CD = Perimeter – 2 AD, = 52 – 2 × 10
Page 16 :
= 52 – 20, = 32 cm, Thus, area of trapezium = ½ × (sum of parallel sides) × altitude, = ½ × 32 × 8, = 128 cm2, , 8. The area of a trapezium is 540 cm2. If the ratio of parallel sides is 7 : 5 and, the distance between them is 18 cm, find the lengths of parallel sides., Solution:, , Let’s assume the two parallel sides of trapezium to be 7x and 5x., Height = 18 cm, Now,, Area of trapezium = ½ × [Sum of || gm sides × height], ⇒ 540 = ½ × (7x + 5x) × 18, 540 = ½ × 12x × 18, 540 = 108x, x = 540/108, x = 5 cm, Hence, the two parallel sides are:, 7x = 7 × 5 = 35 cm and 5x = 5 × 5 = 25 cm, , 9. Calculate the area enclosed by the given shapes. All measurements are in, cm.
Page 17 :
Solution:, , (i) Firstly,, Area of trapezium ABCD, = (Sum of opposite ||gm sides) × height, , = [(AB + CD) × (AF + FD)]
Page 18 :
= [(AB + CD) × (AF + FD), = [(5 + 3) × (5 + 4)], = (5 + 3) × 9, = 36 cm2, Secondly,, Area of rectangle GAFE = Length × Breadth, = 2 × 5 = 10 cm2, Hence,, Total area of the figure = Area of trapezium ABCD + Area of rectangle GAFE, = (36 + 10) cm2, = 46 cm2+, (ii) It’s seen that,, , Area of given figure = Area of rect. ABCD + Area of ||, gm BIHJ + Area of rectangle EFGH, Area of rectangle ABCD = Length × Breadth, = AD × DC, = 9 × 2 = 18 cm2, And,, Area of rectangle EFGH = Length × Breadth
Page 19 :
= (EJ + JH) × EF, = (7 + 2) × 2, = 9 × 2 = 18 cm2, Now,, Area of parallelogram BIHJ = 2 × 5 = 10 cm2, , [Since, distance between BI and HJ = 9 – 2 – 2 = 5 cm], Hence,, Total area of the figure = (18 + 18 + 10) cm2 = 46 cm2, , 10. From the adjoining sketch, calculate, (i) the length AD, (ii) the area of trapezium ABCD, (iii) the area of triangle BCD, , Solution:, , (i) In right angled ∆ ABD, by Pythagoras Theorem we have, BD2 = AD2 + AB2, ⇒ AD2 = BD2 – AB2, = (41)2 – (40)2, = 1681 – 1600, = 81, ∴ AD = √81 = 9 cm
Page 20 :
(ii) Area of trapezium ABCD, = (Sum of opposite || gm lines) × height, = (AB + CD) × AD, = (40+ 15) × 9, = 247.5 cm2, (iii) Area of triangle BCD = Area of trapezium ABCD – Area of ∆ ABD, = (247.5 – × 40 × 9) cm2, = (247.5 – 180) cm2, = 67·5 cm2, , 11. Diagram of the adjacent picture frame has outer dimensions = 28 cm ×, 32 cm and inner dimensions 20 cm × 24 cm. Find the area of each section of, the frame, if the width of each section is same., , Solution:, , Given,, Outer length of the frame = 32 cm and outer breadth = 28 cm, Inner length = 24 cm and outer breadth = 20 cm, So, width of the frame = (32 – 24)/ 2 = 4 cm, ⇒ Height = 4 cm
Page 21 :
Now, area of each portion of length side, = ½ × (24 + 32) × 4, = ½ × 56 × 4, = 112 cm2, And,, Area of each portion of breadth side, = ½ × (20 + 28) × 4, = ½ × 48 × 4, = 96 cm2, Therefore,, Area each section are 112 cm2, 96 cm2, 112 cm2, 96 cm2., , 12. Top surface of a raised platform is in the shape of a regular octagon as, shown in the given figure. Find the area of the octagonal surface., , Solution:, , The raised surface of platform is in the shape of regular octagon ABCDEFGH of each, side = 8 cm.
Page 22 :
Join HC., GD = HC = 15 cm, FL = AM = 6 cm, Now, in each trapezium parallel sides are 15 cm and 6 cm and height = 6 cm, So, Area of each trapezium FEDG = ½ (GD + FE) × FL, = ½ (15 + 8) × 6, = 23 × 3 cm2, = 69 cm2, Also,, Area of trapezium FEDG = Area of trapezium ABCH = 69 cm2, And area of rectangle HCDG = HC × CD, = 15 × 8, = 120 cm2, Hence,, Total area = Area of trapezium FEDG + Area of trapezium ABCH + Area of rectangle, HCDG., = 69 + 69 + 120, = 258 cm2
Page 23 :
13. There is a pentagonal shaped park as shown in the following figure:, For finding its area Jaspreet and Rahul divided it in two different ways., , Find the area of this park using both ways. Can you suggest some other way, of finding its area?, Solution:, , The pentagonal shaped park is shown in the given figure., In which DL ⊥ CE and is produced to M., So, DM = 32 m, LM = CB = 18 m, ∴ DL = 32 – 18 = 14 m, (i) According to Jaspreet’s the figure is divided into two equal trapezium in area: DEAM, and DCBM
Page 24 :
Now,, Area of trapezium DEAM = ½ (AE + DM) × AM, = ½ (32 + 18) × 9, = (50 x 9)/ 2, = 225m2, (ii) According to Rahul’s the figure is divided into shapes: one square and on isosceles, triangle.
Page 25 :
Area of square ABCE = (Side)2, = (18)2, = 324 m2, And, area of isosceles ∆EDC = ½ × EC × DC, = ½ × 18 × 14, = 126 m2, ∴ Total area = 225 × 2 = 450 m2, The third way to find out the area of given figure is as follow:
Page 26 :
Here, DL ⊥ ED and DL = 14 m, Area of ∆DEC = ½ × EC × LD, = ½ × 18 × 14, = 126 m2, Area of ∆AEB = ½ × AB × AE, = ½ × 18 × 18, = 162 m2, Area of ∆BEC = ½ × BC × EC, = ½ × 18 × 18 = 162 m2, Hence, area of pentagon ABCDE = Area ∆DEC + Area of ∆AEB + Area of ∆BEC, = (126 + 162 + 162) m2, = 450 m2, , 14. Polygon ABCDE is divided into parts as shown in the given figure. Find its, area if AD = 8 cm, AH = 6 cm, AG = 4 cm, AF = 3 cm and perpendiculars BF =
Page 27 :
2 cm, CH = 3 cm, EG = 2.5 cm., , Solution:, , In the given figure, ABCDE, AD = 8 cm, AH = 6 cm, AG = 4 cm,, AF = 3cm ⊥ BF = 2 cm CH = 3 cm and ⊥ EG = 2.5 cm, , The given figure, consists of 3 triangles and one trapezium., Now,
Page 28 :
Area of ∆AED = ½ × AD × GE, = ½ × 8 × 2.5, = 10 cm2, Area of ∆ABF = ½ × AF × BF, =½×3×2, = 3 cm2, Area of ∆CDH = ½ × HD × CH, = ½ × (AD – AH) × 3, = ½ × (8 – 6) × 3, =½×2×3, = 3 cm2, Area of trapezium BFHC = ½ × (BF + CH) × FH, = ½ × (2 + 3) × (AH – AF), = ½ × 5 × (6 – 3), =½×5×3, = 7.5 cm2, Hence,, Total area of the figure = Area of ∆AED + Area of ∆ABF + Area of ∆CDH + Area of, trapezium BFHC, = 10 + 3 + 3 + 7.5, = 23.5 cm2, , 15. Find the area of polygon PQRSTU shown in 1 the given figure, if PS = 11, cm, PY = 9 cm, PX = 8 cm, PW = 5 cm, PV = 3 cm, QV = 5 cm, UW = 4 cm, RX, = 6 cm, TY = 2 cm.
Page 29 :
Solution:, , In the figure PQRSTU, we have, PS = 11 cm, PY = 9 cm, PX = 8 cm, PW = 5 cm, PV = 3 cm, QV = 5 cm, UW = 4 cm, RX = 6, cm and TY = 2 cm, And,, The figure consists of 4 triangle and 2 trapeziums, From the figure its seen that,, VX = PX – PV, =8–3, = 5 cm, XS = PS – PX, = 11 – 8, = 3 cm, YS = PS – PY, = 11 – 9, = 2 cm, WY = PY – PW
Page 31 :
1. The volume of a cube is 343 cm3, find the length of an edge of cube., Solution:, , Given,, Volume of a cube = 343 cm3, Let’s consider ‘a’ to be the edge of cube, then, V = a3 = 343 = (7)3, ∴ a = 7 cm, , 2. Fill in the following blanks:, Volume, of, cuboid, , Length, , Breadth, , Height, , (i), , 90 cm3, , –, , 5 cm, , 3 cm, , (ii), , –, , 15 cm, , 8 cm, , 7 cm, , (iii), , 62.5 m3, , 10 cm, , 5 cm, , –, , Solution:, Volume of cuboid = length x Breadth x Height, (i) 90 cm3 = length x 5 cm x 3 cm, Length = 90/(5 x 3) = 90/15 = 6 cm, (ii) Volume = 15 cm x 8 cm x 7 cm, = 840 cm3, (iii) 62.5 m3 = 10 m x 5 m x height, Height = 62.5/(10 x 5) = 1.25 m
Page 32 :
Volume, of, cuboid, , Length, , Breadth, , Height, , (i), , 90 cm3, , 6 cm, , 5 cm, , 3 cm, , (ii), , 840, cm3, , 15 cm, , 8 cm, , 7 cm, , (iii), , 62.5 m3, , 10 cm, , 5 cm, , 1.25, m, , 3. Find the height of a cuboid whose volume is 312 cm3 and base area is 26, cm2., Solution:, , Given,, Volume of a cuboid = 312 cm3, Base area = l × b = 26 cm2, ∴ Height= Volume/Base area = 312/26 = 12cm, , 4. A godown is in the form of a cuboid of measures 55 m × 45 m × 30 m. How, many cuboidal boxes can be stored in it if the volume of one box is 1.25 m 3?, Solution:, Given,, Length of a godown (l) = 55 m, Breadth (b) = 45 m, Height (h) = 30 m, So,, Volume = l × b × h
Page 33 :
= (55 × 45 × 30) m3, = 74250 m3, Also given, volume of one box = 1.25 m3, Thus,, Number of boxes = 74250/1.25 = 59400 boxes, , 5. If each edge of a cube is tripled, then find how many times will its volume, become?, Solution:, , Let’s consider the edge of a cube to be x, Then, it’s volume = x3, Now, if the edge is tripled, Edge = 3x, So, volume = (3x)3 = 27x3, ∴ Its volume is 27 times the volume of the given cube., , 6. A milk tank is in the form of cylinder whose radius is 1.4 m and height is 8, m. Find the quantity of milk in litres that can be stored in the tank., Solution:, , Given,, Radius of the milk cylindrical tank = 1.4 m and height (h) = 8 m, Hence,, Volume of milk in the tank = πr2h, = (22/7) × 1.4 × 1.4 × 8 m3, = 49.28 m3, = 49.28 × 1000 litres, = 49280 litres, Therefore, the quantity of the tank is 49280 litres.
Page 34 :
7. A closed box is made of 2 cm thick wood with external dimension 84 cm ×, 75 cm × 64 cm. Find the volume of the wood required to make the box., Solution:, , Given,, Thickness of the wood used in a closed box = 2 cm, External length of box (L) = 84 cm, Breadth (b) = 75 cm and height (h) = 64 cm, So, internal length (l) = 84 – (2 × 2), = 84 – 4, = 80 cm, Breadth (b) = 75 – (2 × 2), = 75 – 4, = 71 cm, and height (h) = 64 – (2 × 2), = 64 – 4, = 60 cm, Hence, Volume of wood used = 84 × 75 × 64 – 80 × 71 × 60 cm3, = 403200 – 340800 cm3, = 62400 cm3, , 8. Two cylindrical jars contain the same amount of milk. If their diameters, are in the ratio 3 : 4, find the ratio of their heights., Solution:, , Given,, Ratio in diameters of two cylindrical jars = 3 : 4, But their volumes are same., Let’s assume h1 and h2 to be the heights of the two jars respectively.
Page 35 :
Let radius of the first jar (r1) = 3x/2, and radius of the second jar (r2) = 4x/2, Then according to the condition in the problem, we have, , Therefore, the ratio in their heights =16 : 9, , 9. The radius of the base of a right circular cylinder is halved and the height, is doubled. What is the ratio of the volume of the new cylinder to that of the, original cylinder?, Solution:, , Let’s consider the radius of a cylinder to be r, And height = h, So,, Volume = πr2h, Now, its radius is halved and height is doubled, then, Volume = π(r/2)2 × (2h), = πr2h/ 2, Thus, the ratio in the volumes of the new cylinder to old one is, = πr2h/ 2 : πr2h
Page 36 :
=1:2, , 10. A rectangular piece of tin of size 30 cm × 18 cm is rolled in two ways,, once along its length (30 cm) and once along its breadth. Find the ratio of, volumes of two cylinders so formed., Solution:, , Given,, Size of rectangular tin plate = 30 cm × 18 cm, (i) When rolled along its length (30 cm),, Then, the circumference of the circle so formed = 30 cm, Radius(r1) = C/2π = (30 x 7)/ (2 x 22) = 105/22 cm, And height (h1) = 18 cm, Then, volume = πr12h1 = π x (105/22)2 x (18) cm3, If it is rolled along its breadth (18 cm) then,, Circumference = 18 cm, So, radius (r2) = C/2π = (18 x 7)/ (2 x 22) = 63/22 cm, And height (h2) = 30 cm, Then, volume = πr22h2 = π x (63/22)2 x (30) cm3, Now, ratio between the two volumes, = π x (105/22)2 x (18) : π x (63/22)2 x (30), = (105/22)2 x (18) : (63/22)2 x (30), =5:3, , 11. Water flows through a cylindrical pipe of internal diameter 7 cm at 5 m, per sec. Calculate, (i) the volume in litres of water discharged by the pipe in one minute., (ii) the time in minutes, the pipe would take to fill an empty rectangular tank, of size 4 m × 3 m × 2.31 m., Solution:
Page 37 :
Given,, Speed of water flow through cylindrical pipe = 5 m/sec., Internal diameter of the pipe = 7 cm, So, radius (r) = 7/2 cm, Now, length of water flow in 1 minutes (h) = 5 × 60 = 300 m, ∴ Volume of water = πr2h, = 22/7 x 7/2 x 7/2 x 300 x 100 cm3, = 1155000 cm3 = 1155 litres, (i) the volume of water = 1155000 cm3, Volume of rectangular tank of size = 4m × 3m × 2.31m, = 27.72 m3, Also given, speed of water = 4 m/sec., Radius of pipe = 7/2 cm, Volume of water in 1 sec = 22/7 x 7/2 x 7/2 x 5 x 100 cm3, = 19250 cm3, Hence,, (ii) Time taken to empty the tank = 27.72 m3/ 19250, = (2772 x 100 x 100 x 100)/(100 x 19250) sec, = 1440 sec, = 1440/60 = 24 minutes, , 12. Two cylindrical vessels are filled with milk. The radius of one vessel is 15, cm and height is 40 cm, and the radius of other vessel is 20 cm and height is, 45 cm. Find the radius of another cylindrical vessel of height 30 cm which, may just contain the milk which is in the two given vessels., Solution:, , Given,, Radius of one cylinder (r1) = 15 cm, And height (h1) = 40 cm
Page 38 :
Radius of second cylinder (r2) = 20 cm, And height (h2) = 45 cm, Now,, Volume of first cylinder = πr12h1, = 22/7 x 15 x 15 x 40 cm3, = 198000/7 cm3, And,, Volume of second cylinder = πr22h2, = 22/7 x 20 x 20 x 45, = 396000/7 cm3, So, total volume = (198000/7 + 396000/7) cm3, = 594000/7 cm3, Now, volume of third cylinder = 594000/7 cm3, And height = 30 cm, Thus,, , = √900 = 30 cm, ∴ Radius of the third cylinder = 30 cm, , 13. A wooden pole is 7 m high and 20 cm in diameter. Find its weight if the, wood weighs 225 kg per m3., Solution:, , Given,, Height of pole (h) = 7 m, Diameter = 20 cm, So, radius (r) = 20/2 = 10 cm = 10/100 = 1/10 m, And,
Page 39 :
Volume = πr2h, = 22/7 x 1/10 x 1/10 x 7 m3, = 22/100 m3, Weight of wood = 225 kg per m3, Hence,, Total weight = 225 × (22/100) = 99/2 = 49.5 kg, , 14. A cylinder of maximum volume is cut from a wooden cuboid of length 30, cm and cross-section a square of side 14 cm. Find the volume of the cylinder, and the volume of the wood wasted., Solution:, , A cylinder of the maximum volume is cut from a wooden cuboid of length 30 cm and, cross-section a square side 14 cm., , So,, Diameter of the cylinder = 14 cm, ⇒ Radius (r) = 14/2 = 7 cm, and height (h) = 30 cm
Page 40 :
Volume of cuboid = 30 × 14 × 14 = 5880 cm3, Volume of cylinder = πr2h, = 22/7 × 7 × 7 × 30, = 4620 cm3, Hence,, The wastage of wood = 5880 – 4620 = 1260 cm3, , Exercise 15.4, 384 cm2. Find, (i) the length of an edge, (ii) volume of the cube., Solution:, , Given,, Surface area of a cube = 384 cm2, (i) Surface area of cube = 6(side)2, Hence, edge (side) = √(surface area/6), = √(384/6), = √64, = 8 cm, (ii) Volume = (Edge)3 = (8)3 = 8 × 8 × 8 cm3 = 512 cm3, , 2. Find the total surface area of a solid cylinder of radius 5 cm and height 10, cm. Leave your answer in terms of n., Solution:
Page 41 :
Given,, Radius of a solid cylinder (r) = 5 cm, Height (h) = 10 cm, Hence,, Total surface area = 2πrh + 2πr2, = 2rπ(h + r), = 2π × 5(10 + 5), = π × 10 × 15, = 150π cm2, , 3. An aquarium is in the form of a cuboid whose external measures are 70, cm × 28 cm × 35 cm. The base, side faces and back face are to be covered, with coloured paper. Find the area of the paper needed., Solution:, , Given, a cuboid shaped aquarium, Length (l) = 70 cm, Breadth (b) = 28 cm, and height (h) = 35 cm, Now,, Area of base = 70 × 28 cm3, = 1960 cm3, Area of side face = (28 × 35) × 2 cm2, = 1960 cm2, Area of back face = 70 × 35 cm2, = 2450 cm, Thus, the total area = 1960 + 1960 + 2450 = 6370 cm2, Hence, area of paper required is 6370 cm2.
Page 42 :
4. The internal dimensions of rectangular hall are 15 m × 12 m × 4 m. There, are 4 windows each of dimension 2 m × 1.5 m and 2 doors each of dimension, 1.5 m × 2.5 m. Find the cost of white washing all four walls of the hall, if the, cost of white washing is ₹5 per m2. What will be the cost of white washing if, the ceiling of the hall is also white washed?, Solution:, , Given,, Internal dimension of rectangular hall = 15m × 12 m × 4 m, Now,, Area of 4-walls = 2(l + b) × h, = 2(15 + 12) × 4, = 2 × 27 × 4 m2, = 216 m2, Area of 4 windows of size = (2 × 1.5) × 4 = 12 m2, Area of 2 door of size = 2 × (1.5 × 2.5) = 7.5 m2, So, area of remaining hall = 216 – (12 + 7.5) = 216 – 19.5 m2 = 196.5 m2, And,, Cost of white washing the walls all four halls of the house is at the rate of ₹5 per m 2, = 196.5 × 5 = ₹982.50, Area of ceiling = l × b = 15 × 12 = 180 m2, Cost of white washing = 180 × 5 = ₹900, Therefore, the total cost for white washing = ₹982.50 + 900.00, = ₹1882.50, , 5. A swimming pool is 50 m in length, 30 m in breadth and 2.5 m in depth., Find the cost of cementing its floor and walls at the rate of ₹27 per square, metre., Solution:
Page 43 :
Given,, Length of swimming pool = 50 m, Breadth of swimming pool = 30 m, Depth (Height) of swimming pool = 2·5 m, Now,, Area of floor = 50 × 30 = 1500 m2, Area of four walls = 2 (50 + 30) × 2.5 = 160 × 2.5 = 400 m2, So, the area to be cemented = 1500 m2 + 400 m2 = 1900 m2, Cost of cementing 1m2 = ₹27, Hence,, Cost of cementing 1900m2 = ₹27 × 1900 = ₹51300, , 6. The floor of a rectangular hall has a perimeter 236 m. Its height is 4·5 m., Find the cost of painting its four walls (doors and windows be ignored) at the, rate of Rs. 8.40 per square metre., Solution:, , Given,, Perimeter of Hall = 236 m., Height = 4.5 m, Perimeter = 2 (l + b) = 236 m, Area of four walls = 2 (l + b) × h, = 236 × 4.5, = 1062 m2, We have, cost of painting 1 m2 = ₹8.40, Hence,, Cost of painting 1062 m2 = ₹8.40 × 1062 = ₹8920.80, , 7. A cuboidal fish tank has a length of 30 cm, a breadth of 20 cm and a
Page 44 :
height of 20 cm. The tank is placed on a horizontal table and it is threequarters full of water. Find the area of the tank which is in contact with, water., Solution:, , Given,, Length of tank = 30 cm, Breadth of tank = 20 cm, Height of tank = 20 cm, As the tank is three-quarters full of water, So, the height of water in the tank = (20 x 3)/4 = 15 cm, Hence,, Area of the tank in contact with the water = Area of floor of Tank + Area of 4 walls upto, 15 cm, = 30 × 20 + 2 (30 + 20) × 15, = 600 + 2 × 50 × 15, = 600 + 1500 = 2100 cm2, , 8. The curved surface area of a hollow cylinder is 4375 cm2, it is cut along its, height and formed a rectangular sheet of width 35 cm. Find the perimeter of, the rectangular sheet., Solution:, , Given, curved surface area of a hollow cylinder = 4375 cm2, By cutting it from the height,
Page 45 :
It becomes a rectangular sheet whose width = 35 cm, So, the height of cylinder = 35 cm, And, length of sheet = Area/Height, = 4375/35, = 125 cm, Hence, Perimeter of the sheet = 2(l + b), = 2 × (125 + 35), = 2 × 160, = 320 cm, , 9. A road roller has a diameter 0.7 m and its width is 1.2 m. Find the least, number of revolutions that the roller must take in order to level a playground, of size 120 m × 44 m., Solution:, , Given,, Diameter of a road roller = 0.7 m = 70 cm, So, radius (r) = 70/2 cm = 35 cm = 35/100 m
Page 46 :
and width (h) = 1.2 m, Now,, Curved surface area = 2πrh, = (2 × 22/7 × 35/100 × 1.2) m2, = 264/100 m2, Area of playground = 120 m × 44 m, = 120 × 44 m2, = 5280 m2, Hence, the number of revolution made by the road roller = (5280/264) × 100, = 2000 revolutions, , 10. A company packages its milk powder in cylindrical container whose base, has a diameter of 14 cm and height 20 cm. Company places a label around, the surface of the container (as shown in the figure). If the label is placed 2, cm from top and bottom, what is the area of the label?, Solution:, , Given,, Diameter of cylindrical container = 14 cm, So, radius (r) = 14/2 = 7 cm, And, height (h) = 20 cm, Now,, Width of label = 2 0 – (2 + 2) cm = 20 – 4 = 16 cm, Hence, area of label = 2πrh, = 2 × (22/7) × 7 × 16, = 704 cm2, , 11. The length, breadth and height of a rectangular solid are in the ratio 5 : 4, : 2. If its total surface area is 1216 cm2, find the volume of the solid., Solution:
Page 47 :
Given that the ratio in length, breadth and height of a rectangular solid = 5 : 4 : 2, Total surface area =1216 cm2, Let’s assume the length = 5x, breadth = 4x and height = 2x, Total surface area = 2[5x × 4x + 4x × 2x + 2x × 5x], = 2[20x2 + 8x2 + 10x2 ], = 2 × 38x2, = 76x2, So, 76x2 = 1216, ⇒ x2 = 1216/76 = 16 = (4)2, ∴x=4, Hence, the dimensions of the rectangular solid are, Length = 5 × 4 = 20 cm, Breadth = 4 × 4 = 16 cm, Height = 2 × 4 = 8 cm, and volume = lbh = 20 × 16 × 8 = 2560 cm3, , 12. A rectangular room is 6 m long, 5 m wide and 3.5 m high. It has 2 doors, of size 1·1 m by 2 m and 3 windows of size 1.5 m by 1.4 m. Find the cost of, whitewashing the walls and the ceiling of the room at the rate of ₹5.30 per, square metre., Solution:, Given, Length of room = 6 m, Breadth of room = 5 m, Height of room = 3.5 m, So, Area of four walls = 2 (l + b) × h, = 2 (6 + 5) × 3.5, = 77 m2, Area of 2 doors and 3 windows = (2 × 1.1 × 2 + 3 × 1.5 × 1.4), = (44 + 6.3) m2
Page 48 :
= 10.7 m2, Area of ceiling = l × b = 6 × 5 = 30 m2, Thus,, Total area for white washing = (77 – 10.7 + 30) m2 = 96.3 m2, Hence, the cost of white washing = ₹(96.3 × 5.30) = ₹510.39, , 13. The sum of the radius and height of a cylinder is 37 cm and the total, surface area of the cylinder is 1628 cm2. Find the height and the volume of, the cylinder., Solution:, , Given,, Sum of height and radius of a cylinder = 37 cm, Total surface area = 1628 cm2, Let’s consider the radius to be r, Then, height = (37 – r) cm, Now,, Total surface area = 2π(h + r), , ⇒ r = 7 cm, Height = 37 – 7 = 30 cm, Hence,, Volume = πr2h, = (22/7) × 7 × 7 × 30 cm3, = 4620 cm3
Page 49 :
14. The ratio between the curved surface and total surface of a cylinder is 1 :, 2. Find the volume of the cylinder, given that its total surface area is 616, cm3., Solution:, , Given that ratio between curved surface and total surface area of a cylinder = 1 : 2, Total surface area = 616 cm2, So, curved surface area = 616/2 = 308 cm2, And,, Area of two circular faces = 616 – 308 = 308 cm2, Area of one circular face = 308/2 = 154 cm2, Now, let’s consider the radius to be r, πr2 = 154, (22/7) × r2 = 154, r2 = (154 × 7)/ 22 = 49, ⇒ r = 49 = √7 cm, Hence, the volume = πr2h = (22/7) × 7 × 7 × 7 = 1078 cm2, , 15. The given figure shown a metal pipe 77 cm long. The inner diameter of, cross section is 4 cm and the outer one is 4.4 cm., Find its, (i) inner curved surface area, (ii) outer curved surface area, (iii) total surface area., Solution:
Page 50 :
Given,, Length of metal pipe (h) = 77 cm, Inner diameter = 4 cm, and outer diameter = 4.4 cm, So, inner radius (r) = 4/2 = 2 cm, And outer radius (R) = 4.4/2 = 2.2 cm, (i) Inner curved surface area = 2πrh, = 2 × 22/7 × 2 × 77 cm2, = 968 cm2, (ii) Outer surface area = 2πRH, = 2 × 22/7 × 2.2 × 77 cm2, = 1064.8 cm2, (iii) Surface area of upper and lower rings = 2[πR 2 – πr2], = 2 × 22/7 (2.22 – 22) cm2
Page 51 :
= 44/7 × 4.2 × 0.2, = 5.28 cm2, Hence,, Total surface area = (968 + 1064.8 + 5.28) cm2 = 2038.08 cm2