Page 1 :
Class: VIII, Squares and Square Roots
Page 2 :
Following topics we are going to cover, inside the lesson;, Introduction about square numbers, Properties of square numbers., Some interesting Patterns over square, numbers., Finding the square of a number, Pythagorean triplets, Finding square root, Estimating square roots
Page 3 :
Objectives of this lesson:, At the end of the lesson you will able to;, , Define the square numbers., Know the Properties of square numbers., Make interesting Patterns over square, numbers., Find the square of a number by prime, factorization and division method., Estimate the square root of a number.
Page 4 :
Square Number:, , The square of a number is the product of the, number with the number itself., Altematively, the square of a number is obtained, by raising the number to the power 2., Thus, if a is a number, then the square of a is (a, x a), denoted by a², For example:, ① 3² = 3 × 3 = 9, so we say that square of 3 is 9., , ② 7² = 7 × 7 = 49, so we say that square of 7 is 49.
Page 5 :
In other words;, Any natural number ‘p’ which can be represented as y²,, where y is a natural number, then ‘p’ is called a Square, Number., Example:, 4 = 2², 9 = 3², 16 = 4² Where 2, 3, 4 are the natural numbers and 4, 9, 16, are the respective square numbers., Such types of numbers are also known as Perfect Squares.
Page 6 :
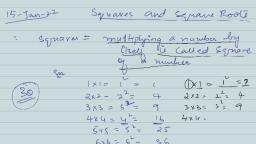
Some of the Square Numbers
Page 7 :
Properties of Square Numbers:, 1. We can see that, the square numbers, are ending with, 0, 1, 4, 5, 6 or 9 only., None of the square, number is ending, with 2, 3, 7 or 8.
Page 8 :
2. Any number having 1 or 9 in its one’s place, will always have a square ending with 1.
Page 9 :
3. Any number which has 4 or 6 in its unit’s place,, its square will always end with 6.
Page 10 :
4. Any number which has 0 in its unit’s place, its, square will always have an even number of zeros, at the end.
Page 11 :
5. The units digit of the square of a number can, be determined if the units digit of the number is, known.
Page 12 :
6. The square of an even number is always even., For example: 2² = 4, 4² = 16, 6² = 36 etc., 7. The square of an odd number is always odd., For example: 1² = 1, 3² = 9, 5² = 25 etc., 8. If a number divided by 3 leaves a remainder 2,, then it is not a perfect square., In other words, the square of a natural number, other than 1 is either a multiple of 3 or excecds, the multiple of 3 by 1.
Page 13 :
For example:, , 2² = 4 = 3×1+1, 3² = 9 = 3×3, 4² = 16 = 3×5+1, 5² = 25 = 3×8+1, 6² = 36 = 3×12, , Thus, square of a natural number other than, one can be expressed as 3n or 3n + 1.
Page 14 :
9. If a number divided by 4 leaves a remainder 2, or 3, then it is not a perfect square., In other words, the square of a natural number, other than 1 is either a multiple of 4 or exceeds a, multiple of 4 by 1., 2² = 4 = 4×1, For example:, 3² = 9 = 4×2+1, 4² = 16 = 4×4, 5² = 25 = 4×6+1, 6² = 36 = 4×9
Page 15 :
Thus, square of a natural number other than, one can be expressed as 4n or 4n + 1., , Note:, If a nuwmber leaves remainder O or 1 when, divided by 4, it is not necessarily a perfect, square. However, if it leaves remainder other, than O and 1, it is definitely not a perfect, square.
Page 16 :
Self assessment:, 1. Which of the following numbers are not a perfect, squares., I. 1857, II. 1681, III. 8281, IV. 8392, 2. Which of the following are squares of even, numbers?, I. 1444, II. 729, III. 8649, IV. 3844, 3. Which of the following are squares of odd, numbers?, I. 1296, II. 5329, III. 625, IV. 8392
Page 17 :
10. If 1 is added to the product of two, consecutive odd natural numbers, then the, result obtained is equal to the square of, the only even natural number between, them., For example: 3 x 5 + 1 = 16 = 4², 7 x 9 + 1 = 64 = 8²
Page 18 :
12. If 1 is added to the product of two, consecutive even natural numbers, then, the result obtained is equal to the square, of the only odd natural number between, them., For example: 2 x 4 + 1 = 9 = 3², 8 x 10 + 1 = 81 = 9²
Page 19 :
13. The Product of Two Consecutive, Even or Odd Natural Numbers:, If we have two consecutive odd or even numbers, (a + 1) and (a -1) then their product will be (a² - 1), Example:, Let take two consecutive odd numbers 21 and 23., 21 × 23 = (22 - 1) × (22 + 1) = 22² - 1 = 483, Let take two consecutive even numbers 38 and 40., 38 × 40 = (39 - 1) × (39 + 1) = 39² - 1 = 1520
Page 20 :
Interesting Patterns over square numbers:, , Triangular Numbers:, , A triangular number counts objects arranged, in an equilateral triangle., The nth triangular number is the number of, dots in the triangular arrangement with n, dots on a side, and is equal to the sum of the, n natural numbers from 1 to n.
Page 22 :
Alternately, Any of the series of numbers, obtained by continued summation of the, natural numbers are called triangular numbers., , Natural number, , Triangular number, , 1, , 1, , 1+2, , 3, , 1+2+3, , 6, , 1+2+3+4, , 10
Page 23 :
1. Adding Triangular Numbers:, If we add two consecutive triangular numbers, then we can get the square number., Triangular number, 1+3, 3+6, 6 + 10, 10 + 15, , Square number, 4, 9, 16, 25
Page 24 :
Pictorial representation for adding two consecutive, triangular numbers make a square number:
Page 25 :
2. Numbers between Square, Numbers:, If we take two consecutive numbers n, and n + 1, then there will be (2n) nonperfect square numbers between their, squares numbers.
Page 26 :
Example:, Let’s take n = 5 and 5² = 25, n + 1 = 5 + 1 = 6 and 6² = 36, Then, 2n = 2(5) = 10, There must be 10 numbers between 25 and, 36., The numbers are: 26, 27, 28, 29, 30, 31, 32,, 33, 34, 35.
Page 27 :
Self assessment:, 1. When you add two consecutive triangular number, then which type of number you get?, 2. Find the 15th triangular number., 3. How many non perfect square numbers between, the square of 15 and 16., 4. There are 48 non perfect square numbers between, two perfect square numbers. Then find the largest, perfect square number among them.
Page 28 :
3. Adding Odd Numbers, , Sum of first n natural odd numbers is n².
Page 29 :
Any square number must be the sum of, consecutive odd numbers starting from 1., , Note: If any natural number which is not a, sum of successive odd natural numbers, starting with 1, then it will not be a perfect, square.
Page 30 :
4. A Sum of Consecutive, Natural Numbers, The square of any odd natural number, other than 1 can be expressed as the, sum of two consecutive natural numbers.
Page 31 :
For example:, 3² = 9 = 4+5, 5² = 25 = 12+ 13, 7² = 49 = 24+25, 9² = 81 = 40 + 41, etc.
Page 32 :
5. Difference between the square of two, consecutive natural numbers:, The ditference between the square of two, consecutive natural numbers is equal to the sum of, the numbers or twice the smaller number plus one., Let the two consecutive numbers be n and n+1., Then, (n+1)² - n² = (n +1 + n)(n + 1 - n), [Using a² - b² = (a+ b)(a - b)], , = (2n + 1)(1) = (2n + 1) = (n + 1) + n, ∴ (n + 1)² - n² = {(n + 1) + n}
Page 33 :
For example:, {(92)², , - (91)²} = 92 +91 = 183, , Or, 2×91 + 1 = 182 + 1 = 183, {(37)², , - (36)²} = 37 + 36 = 73, , Or, 2×36 + 1 = 72 + 1 = 73
Page 34 :
6. Squares of natural numbers having all, digits 1 follow the following pattern.
Page 35 :
7. Some More Interesting Patterns about, Square Numbers:
Page 36 :
Finding the Square of a Number:, To find the square of any number we, needed to divide the number into two parts, then we can solve it easily., If number is ‘x’ then x = (p + q) and, x² = (p + q)², You can also use the formula, (p + q)² = p² + 2pq + q²
Page 37 :
Example: Find the square of 53., Solution:, Divide the number in two parts., 53 = 50 + 3, 53² = (50 + 3)², = (50 + 3) (50 + 3), = 50(50 + 3) +3(50 + 3), = 2500 + 150 + 150 + 9, = 2809
Page 38 :
Other pattern for the number ending with 5, For numbers ending with 5 we can use the pattern, (a5)² = a × (a + 1)100 + 25, Example:, 25² = 625 = (2 × 3) 100 + 25, 45² = 2025 = (4 × 5) 100 + 25, 95² = 9025 = (9 × 10) 100 + 25, 125² = 15625 = (12 × 13) 100 + 25
Page 39 :
Pythagorean Triplets:, If the sum of two square numbers is also, a square number, then these three, numbers form a Pythagorean triplet., For any natural number p >1, we have, (2p)² + (p² -1)² = (p² + 1)², So, 2p, (p² - 1) and (p² + 1) forms a, Pythagorean triplet.
Page 40 :
Square Roots, The square root is the inverse operation of squaring. To find, the number with the given square is called the Square Root., 2² = 4, so the square root of 4 is 2, 10² = 100, therefore square root of 100 is 10, There are two square roots of any number. One is positive, and other is negative., The square root of 100 could be 10 or -10., , Symbol of Positive Square Root, , ➡
Page 41 :
Finding Square Root, 1. Through Repeated Subtraction, As we know that every square number is the sum of, consecutive odd natural numbers starting from 1, so we can, find the square root by doing opposite because root is the, inverse of the square., We need to subtract the odd natural numbers starting from 1, from the given square number until the remainder is zero to get, its square root., The number of steps will be the square root of that square, number.
Page 42 :
Example: Calculate the square root of 64 by repeated addition, Solution: 64 – 1 = 63, 63 – 3 = 60, 60 – 5 = 55, 55 – 7 = 48, 48 – 9 = 39, 39–11 = 28, 28–13 = 15, 15–15 = 0, Hence, square root of 64 is 8
Page 43 :
2. Prime Factorization, In this method, we need to list the prime factors of the given, number and then make the pair of two same numbers., Then write one number for each pair and multiply to find the, square root., Example: Calculate the square root of 784 using prime, factorization method., Solution: List the prime factors of 784., 784 = 2 × 2 × 2 × 2 × 7 × 7, √784 = 2 × 2 × 7 = 28
Page 44 :
3. Division Method, Steps to find the square root by division method, Step 1: First we have to start making the pair of digits, starting from the right and if there are odd number of digits, then the single digit left over at the left will also have bar ., Step 2: Take the largest possible number whose square is, less than or equal to the number which is on the first bar, from the left. Write the same number as the divisor and the, quotient with the number under the extreme left bar as the, dividend. Divide to get the remainder.
Page 45 :
Step 3: Like a normal division process bring the digits in, next bar down and write next to the remainder., Step 4: In next part the quotient will get double and we will, right in next line with a blank on its right., Step 5: Now we have to take a number to fill the blank so, that the if we take it as quotient then the product of the new, divisor and the new digit in quotient is less than or equal to, the dividend., Step 6: If there are large number of digits then you can, repeat the steps 3, 4, 5 until the remainder does not, become 0.
Page 46 :
Example: Calculate the square root of √729 using division, method., Solution:, , Thus, √729 = 27.
Page 47 :
Square Roots of Decimals, To find the square root of a decimal number we have to put, bars on the primary part of the number in the same manner as, we did to find the square root of a perfect square number. And, for the digits on the right of the decimal we have to put bars, starting from the first decimal place., Rest of the method is same as above. We just need to put the, decimal in between when the decimal will come in the division.
Page 48 :
Example: Find √7.29 using division method., Solution:, Remark: To put the, bar on a number like, 174.241, we will put a, bar on 74 and a bar, on 1 as it is a single, digit left. And in the, numbers after, decimal, we will put a, bar on 24 and put, zero after 1 to make it, double-digit., Thus, √7.29 = 2.7, 1 74. 24 10
Page 49 :
Estimating Square Root, Sometimes we have to estimate the square root, of a number if it’s not possible to calculate the, exact square root., Example:, Estimate the square root of 300.
Page 50 :
Solution: We know that, 300 comes between 100 and, 400, i.e. 100 < 300 < 400., Now, √100 = 10 and √400 = 20., So, we can say that, 10 < √300 < 20., We can further estimate the numbers as we know that, 17² = 289 and 18² = 324., Thus, we can say that the square root of √300 = 17 as, 289 is much closer to 300 than 324.