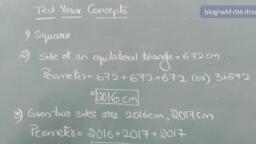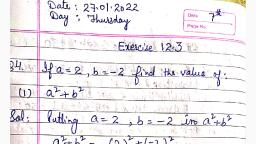Page 1 :
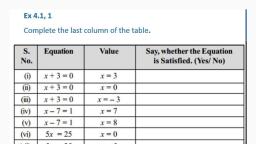
VIVEKANANDA RESIDENTIAL SCHOOL, Class-VII, Subject: MATHEMATICS, Chapter-12, ALGEBRAIC EXPRESSIONS, EXERCISE-12.3, 1. If m = 2, find the value of:, (i) m - 2 = 2 - 2 = 0, (ii) 3m - 5 = (3 x 2) - 5 = 6 - 5 = 1, (iii) 9 - 5m = 9 - (5 x 2) = 9-10 = -1, (iv) 3 m2 - 2m - 7 = 3 x (2 × 2) - (2 x 2) - 7, = 12 - 4 - 7 = 1, 5x2, -4%3D, 5m, -4 = 1, 2, (v), 2. If p = -2, find the value of:, (i) 4p + 7 = 4 x (-2) + 7 = - 8 + 7 = -1, (ii) - 3p2 + 4p + 7 = -3 (-2) × (-2) + 4 × (-2) + 7, = - 12 - 8 + 7 = -13, (iii) -2 p3, 3p2 + 4p + 7, = -2 (-2) x (-2) x (-2) - 3 (-2) x (-2) + 4 x (-2) + 7, = 16 - 12 - 8 + 7 = 3, 3. Find the value of the following expressions, when x = - 1:, (i) 2x - 7= 2 × (-1) - 7 = -9, (ii) - x + 2 = - (-1) + 2 = 1 + 2 = 3, (iii) x2 + 2x + 1 = (-1) x (-1) + 2 x (-1) + 1, = 1 - 2 + 1 = 0, (iv) 2x2 - x - 2 2 (-1) x (-1) - (-1) – 2, = 2 + 1 - 2 = 1, 4. If a = 2, b = - 2, find the value of:, (i) a? + b2= (2)2 + (-2)2 = 4 + 4 = 8, (ii) a2 + ab + b2= (2 x 2) + 2 x (-2) + (-2) × (-2), = 4 - 4 + 4 = 4, - (-2)2 = 4 - 4 = 0, (iii) a2 - b2= (2)2, 5. When a = 0, b = - 1, find the value of the given expressions:, (i) 2a + 2b = 2 x (0) + 2 x (-1) = 0 - 2 = -2, (ii) 2a2 + b2 + 1= 2 x (0)2 + (-1) × (-1) + 1, = 0 + 1 + 1 = 2, (iii) 2a²b + 2ab? + ab- 2 x (0)2 x (-1) + 2 × (0) x (-1) x (-1) + 0 x (-1), = 0 + 0 + 0 = 0, (iv) a? + ab + 2= (0)2 + 0 x (-1) + 2, = 0 + 0 + 2 = 2, 6. Simplify the expressions and find the value if x is equal to 2, (i) x + 7 + 4 (x - 5) = x + 7 + 4x - 20, = x + 4x + 7 - 20, = 5x - 13, = (5 x 2) - 13, = 10 - 13 = -3, (ii) 3 (x + 2) + 5x - 7 = 3x + 6 + 5x - 7, = 3x + 5x + 6 - 7 = 8x - 1, = (8 x 2) - 1 = 16 - 1 =15
Page 2 :
(iii) 6x + 5 (x - 2) = 6x + 5x - 10, 11x - 10, = (11 x 2) - 10 = 22 - 10 = 12, (iv) 4 (2x - 1) + 3x + 11 = 8x - 4 + 3x + 11, = 11x + 7, (11 x 2) + 7, = 22 + 7 =29, 7. Simplify these expressions and find their values if x = 3, a = - 1, b = - 2., (i) 3x - 5 - x + 9 = 3x - x - 5 + 9, = 2x + 4 = (2 x 3) + 4 = 10, (ii) 2 - 8x + 4x + 4 = 2 + 4 - 8x + 4x, = 6 - 4x = 6 - (4 x 3) = 6 - 12 = -6, (iii) 3a + 5 - 8a + 1 = 3a - 8a + 5 + 1, = - 5a + 6 = -5 x (-1) + 6, = 5 + 6 = 11, (iv) 10 - 3b- 4- 5b = 10 - 4- 3b - 5b, = 6 - 8b = 6 - 8 x (-2), = 6 + 16 = 22, (v) 2a - 2b - 4 - 5 + a = 2a + a - 2b - 4 - 5, = 3a - 2b - 9s, = 3 x (-1) - 2 (-2) - 9, = - 3 + 4 - 9 = -8, 8. (i) If z = 10, find the value of z3 - 3 (z - 10)., z3 - 3 (z - 10) = z3 - 3z + 30, (10 x 10 x 10) - (3 x 10) + 30, = 1000 - 30 30 = 1000, (ii) p2 - 2p - 100, = (-10) x (-10) 2 (-10) - 100, = 100 + 20 - 100 = 20, 9. What should be the value of a if the value of 2x2 + x - a equals to 5, when x = 0?, 2x2 + x - a = 5, when x = 0, (2 x 0) + 0 - a = 5, 0 - a = 5, a = -5, 10. Simplify the expression and find its value when a = 5 and b = -3., 2 (a2 + ab) + 3 - ab, 2 a2 + 2 ab + 3 - ab, = 2 a2 + 2ab - ab + 3, = 2 a? + ab + 3, 2 x (5 x 5) + 5 x (-3) + 3, 50 - 15 + 3 = 38, 2 (a2 + ab) + 3 - ab