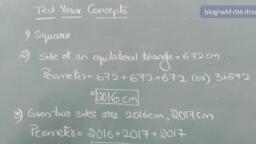Page 1 :
VIVEKANANDA RESIDENTIAL SCHOOL, Class-VII, Subject: MATHEMATICS, Chapter-11, PERIMETER AND AREA, Circle:, • A circle is a simple closed curve which is not a polygon., • A circle is a collection of points which are equidistant from a fixed point., , The fixed point in the middle is called the centre., The fixed distance is known as radius., Circumference of a Circle:, • The circumference of a circle (C) is the total path or total distance covered, by the circle. It is also called a perimeter of the circle., Circumference of a circle = 2×π×r, Area of Circle:, • Area of a circle is the total region enclosed by the circle., Area of a circle = πr2, where r is the radius of the circle., Note: diameter (d) = twice the radius (r), d = 2r, Introduction and Value of Pi:, • Pi (π) is the constant which is defined as the ratio of a, circle’s circumference (2πr) to its diameter (2r)., π= Circumference (2πr)/Diameter (2r), • The value of pi is approximately equal to 3.14(approximately) or 22/7., Conversion of Units:, • Sometimes we need to convert the unit of the given measurements to make, it similar to the other given units., Unit, Conversion, •, •, , 1 cm, 1m, 1 km, 1 hectare(ha), , 10 mm, 100 cm, 1000 m, 100 × 100 m, , Unit, , Conversion, , cm 2, , 100 mm2, 10000 cm 2, 1000000 m 2, 10000 m 2, , 1, 1 m2, 1 km2, 1 ha, , EXERCISE – 11.3
Page 2 :
1. Find the circumference of the circle with the following radius: (Take π = 22/7), (a) 14 cm, Solution:Given, radius of circle = 14 cm, Circumference of the circle = 2πr, = 2 × (22/7) × 14, = 2 × 22 × 2, = 88 cm, (b) 28 cm, Solution:Given, radius of circle = 28 cm, Circumference of the circle = 2πr, = 2 × (22/7) × 28, = 2 × 22 × 4, = 176 cm, (c) 21 cm, r = 21 cm, Circumference = 2πr, , = 132 cm, , 2. Find the area of the following circles, given that:, (a) Radius = 14 mm (Take π = 22/7), Solution:, r = 14 mm, Area = πr 2, , = 616 mm2, , (b) Diameter = 49 m, Solution:, d = 49 m, r =, Area = πr 2 =, (c) Radius = 5 cm, Solution:, r = 5 cm, , = 1886.5 m 2, , Area = πr 2 =, = 78.57 cm 2, 3. If the circumference of a circular sheet is 154 m, find its radius. Also find the, area of the sheet. (Take π = 22/7), Solution:Circumference = 2πr =154 m
Page 3 :
Area = πr 2 =, =, = 1886.5 m 2, 4. A gardener wants to fence a circular garden of diameter 21m. Find the length, of the rope he needs to purchase, if he makes 2 rounds of fence. Also find the, cost of the rope, if it costs ₹ 4 per meter. (Take π = 22/7), , Solution:d = 21 m, r=, Circumference = 2πr =, = 66 m, Length of rope required for fencing = 2 × 66 m = 132 m, Cost of 1 m rope = Rs 4, Cost of 132 m rope = 4 × 132 = Rs 528, 5. From a circular sheet of radius 4 cm, a circle of radius 3 cm is removed. Find, the area of the remaining sheet. (Take π = 3.14), Solution:From the question it is give that,, Radius of circular sheet R = 4 cm, A circle of radius to be removed r = 3 cm, Then,, The area of the remaining sheet = πR2 – πr2, = π (R2 – r2), = 3.14 (42 – 32), = 3.14 (16 – 9), = 3.14 × 7, = 21.98 cm2, So, the area of the remaining sheet is 21.98 cm 2., 6. Saima wants to put a lace on the edge of a circular table cover of diameter 1.5, m. Find the length of the lace required and also find its cost if one meter of the, lace costs ₹ 15. (Take π = 3.14), Solution:From the question it is given that,, Diameter of the circular table = 1.5 m, Circumference = 2πr, , Cost of 1 m lace = Rs 15, Cost of 4.71 m lace = 4.71 × 15 = Rs 70.65
Page 4 :
7. Find the perimeter of the adjoining figure, which is a semicircle including its, diameter., , Solution:From the question it is given that,, Diameter of semi-circle = 10 cm, Radius = 5 cm, Length of curved part = πr, , = 15.71 cm, Total perimeter = Length of curved part + Length of diameter, = 15.71 + 10 = 25.71 cm, 8. Find the cost of polishing a circular table-top of diameter 1.6 m, if the rate of, polishing is ₹15/m2. (Take π = 3.14), Solution:Diameter = 1.6 m, Radius, = 0.8 m, Area = 3.14 × 0.8 × 0.8, = 2.0096 m 2, Cost for polishing 1 m 2 area = Rs 15, Cost for polishing 2.0096 m 2 area = 15 × 2.0096 = 30.14, Therefore, it will cost Rs 30.14 for polishing such circular table., 9. Shazli took a wire of length 44 cm and bent it into the shape of a circle. Find, the radius of that circle. Also find its area. If the same wire is bent into the, shape of a square, what will be the length of each of its sides? Which figure, encloses more area, the circle or the square? (Take π = 22/7), Solution:From the question it is given that,, Length of wire that Shazli took =44 cm, Then,, Circumference = 2πr = 44 cm, , r = 7 cm, Area = πr 2, If the wire is bent into a square, then the length of each side would be =, , Area of square = (11) 2 = 121 cm 2, Therefore, circle encloses more area.
Page 5 :
10. From a circular card sheet of radius 14 cm, two circles of radius 3.5 cm and, a rectangle of length 3 cm and breadth 1cm are removed. (as shown in the, adjoining figure). Find the area of the remaining sheet. (Take π = 22/7), , Solution:From the question it is given that,, Radius of the bigger circle = 14 cm, Radius of the two small circle = 3.5 cm, Length of the rectangle = 3 cm, Breadth of the rectangle = 1 cm, First we have to find out the area of bigger circle, two circles and rectangle to, find out the remaining area., Now,, Area of bigger circle =, , = 616 cm2, , Area of 2 small circles = 2 × πr 2, = 77 cm2, Area of rectangle = Length × Breadth = 3 × 1 = 3 cm 2, Remaining area of sheet = 616 − 77 − 3 = 536 cm 2, 11. A circle of radius 2 cm is cut out from a square piece of an aluminium sheet, of side, 6 cm. What is the area of the left over aluminium sheet? (Take π = 3.14), Solution:From the question it is given that,, Radius of circle = 2 cm, Square sheet side = 6 cm, First we have to find out the area of square aluminium sheet and circle to find, out the remaining area., Now,, Area of square-shaped sheet = (Side) 2 = (6) 2 = 36 cm2, Area of circle = 3.14 × 2 × 2 = 12.56 cm 2, Remaining area of sheet = 36 − 12.56 = 23.44 cm 2, 12. The circumference of a circle is 31.4 cm. Find the radius and the area of the, circle? (Take π = 3.14), Solution:From the question it is given that,, Circumference of a circle = 31.4 cm, We know that,, Circumference = 2πr = 31.4 cm, 2 × 3.14 × r = 31.4, r = 5 cm, Area = 3.14 × 5 × 5 = 78.50 cm 2, 13. A circular flower bed is surrounded by a path 4 m wide. The diameter of the, flower bed is 66 m. What is the area of this path? (π = 3.14)
Page 6 :
Solution:From the question it is given that,, Diameter of the flower bed = 66 m, Radius of flower bed, = 33 m, Radius of flower bed and path together = 33 + 4 = 37 m, Area of flower bed and path together = πr2 = 3.14 × 37 × 37 = 4298.66 m 2, Area of flower bed = πr2 = 3.14 × 33 × 33 = 3419.46 m 2, Area of path = Area of flower bed and path together − Area of flower bed, = 4298.66 − 3419.46 = 879.20 m 2, 14. A circular flower garden has an area of 314 m2. A sprinkler at the centre of, the garden can cover an area that has a radius of 12 m. Will the sprinkler water, the entire garden? (Take π = 3.14), Solution:From the question it is given that,, Area of the circular flower garden = 314 m2, Sprinkler at the centre of the garden can cover an area that has a radius = 12, m, Area of the circular flower garden = πr2, 314 = 3.14 × r2, 314/3.14 = r2, r2 = 100, r = √100, r = 10 m, ∴Radius of the circular flower garden is 10 m., Since, the sprinkler can cover an area of radius 12 m, Hence, the sprinkler will water the whole garden., 15. Find the circumference of the inner and the outer circles, shown in the, adjoining figure? (Take π = 3.14), , Solution:From the figure,, Radius of inner circle = outer circle radius – 10, = 19 – 10, =9m, Circumference of the inner circle = 2πr, = 2 × 3.14 × 9, = 56.52 m, Then,, Radius of outer circle = 19 m, Circumference of the inner circle = 2πr
Page 7 :
= 2 × 3.14 × 19, = 119.32 m, 16. How many times a wheel of radius 28 cm must rotate to go 352 m? (Take π =, 22/7), Solution:From the question it is given that,, Radius of the wheel = 28 cm, Circumference = 2πr =, , = 176 cm, , Number of rotations =, Therefore, it will rotate 200 times., 17. The minute hand of a circular clock is 15 cm long. How far does the tip of, the minute hand move in 1 hour. (Take π = 3.14), Solution:From the question it is given that,, Length of the minute hand of the circular clock = 15 cm, Then,, Distance travelled by the tip of minute hand in 1 hour = circumference of, the clock, = 2πr, = 2 × 3.14 × 15, = 94.2 cm