Page 3 :
Electric charge and field, , Batch -PARAKRAM, Electrostatics-, , Electrostatics , deals with the study of charges in rest. These stationary charges occurs due to, friction of two insulating bodies, therefore it is often called frictional electricity, , ❑ Charge, Charge is the property associated with matter due to which it produces, and experiences electrical and magnetic effects., Charge at rest, Velocity=0, , E Only, , Charge in uniform motion, Velocity = Constant, , E & B both, , Accelerated charge, Velocity ≠ 𝑪𝒐𝒏𝒔𝒕𝒂𝒏𝒕, , E, B and radiation of EMW, , Charges are of two types., (a) Positive charge : Lesser number of, electrons than number of protons., (b) Negative charge : More number of, electrons than number of protons, , ✓ Only , electron is responsible for a substance to be charged and not the proton., , Unit, S.I. unit of charge is Ampere sec = coulomb (C), smaller S.I. units, are mC, mC., C.G.S. unit of charge is Stat coulomb or e.s.u. Electromagnetic unit, of Ab coulomb, ✓ Smallest unit of charge is Frankline and largest is Faraday, 1 coulomb = 3 × 109 e.s.u.(Frankline) = 1/10 e.m.u., 1 Faraday = 96500 C., , Properties of Charge :, (i) Like charges repel while unlike charges attract each other., (ii) Charge is quantized in nature i.e. The magnitude of charge possessed by different, objects is always an integral multiple of charge of electron (or proton) i.e. q = ± ne where, n = 1 , 2 , 3 ........, (iii) The minimum possible charge that can exist in nature is the charge of electron which, has a magnitude of e = 1.6x10-19 coulomb. This is also known as quantum of charge or, fundamental charge., (iv) In an isolated system the algebraic sum of total charge remains constant. This is the law, of 'Conservation of charge'., (v) Charge is invariant (It does not depends on speed), (vi) Charge can not be massless., , ❑ Methods of Charging, (1) By friction : By rubbing two bodies, together, both positive and negative, charges in equal amounts appear, simultaneously due to transfer of, electrons from one body to the other., , Group 1, (+ve), , Group 2, (-ve), , Glass rod, , Silk cloth, , Catskin, , Plastic rod, Ebonite rod, , Woolen, cloth, , Plastic rod, Ebonite rod, Amber,, Rubber, , Method Guru - Shashtrinagar, Sultanpur (UP) Mob. 7014344748
Page 4 :
Electric charge and field, , Batch -PARAKRAM, , -, , +, uncharged body, , Uncharged Body, , Rubbing, , Both Charged, , (2) By Conduction:, Take two conductors, one charged and other uncharged. Bring the, conductors in contact with each other. The charge under its own, repulsion will spread over both the conductors. Thus the conductors will, be charged with the same sign. This is called as charging by conduction, (through contact)., , +, Charged body, , +, Uncharged Body, , +, , Contact, , +, Both Charged, , (3) By Induction:, If a charged body is brought near an uncharged body, one side of, neutral body (closer to charged body) becomes oppositely charged while, the other side becomes similarly charged., , +, , -, , Induced charge can be lesser or equal to inducing charge (but never greater) and, its maximum value is given by, 1, , Q' = −Q1 − , K, , , where Q is the inducing charge and K is the dielectric constant of the material of the uncharged body, , Dielectric constant for different materials, Medium, , K, , Medium, , K, , Vacuum, air, Paraffin vax, Rubber, Transformer oil, Glass, , 1, 1.0003, 2.1, 3, 4.5, 5–10, , Mica, Silicon, Germanium, Glycerin, Water, Metal, , 6, 12, 16, 50, 80, , , Method Guru - Shashtrinagar, Sultanpur (UP) Mob. 7014344748
Page 5 :
Electric charge and field, , Batch -PARAKRAM, ontact)., ❑ Gold, leaf Electroscope(GLE)-, , This is used to➢ Detect the presence of charge on body., ➢ Compare the charge on two bodies., ➢ Detect the nature of charge ., , ❑, , Charge Distribution, , Continuous charge distribution, , Linear charge distribution, , Discrete charge distribution, , Surface charge distribution, , ++, ++, , ++++++++++, Linear charge density, (Charge per unit length), , =, , Charge, =, Length, , Surface charge density, (Charge per unit area), , 𝑞, 𝐿, , =, , Unit- C/m, , Charge, =, Area, , 𝑞, 𝐴, , 𝑞, 2𝜋𝑅, , Uniformly Charged ring, , 𝜎=, , Volume charge density, (Charge per unit volume), , =, , Charge, =, Volume, , 𝑞, 𝑉, , Unit- 𝐶ൗ𝑚𝟑, , Unit- 𝐶ൗ𝑚2, , Example:, , 𝜆=, , Volume charge distribution, , 𝑞, 4𝜋𝑅 2, , Uniformly Charged conducting sphere, , 𝜌=, , 𝑞, 4 3, 𝜋𝑅, 3, , Uniformly Charged non-conducting sphere, , ❑ Charge on a conductor:, ➢ Charge given to a conductor always resides on it's outer surface., ➢ This is why a solid and hollow conducting sphere of same outer radius will, hold maximum equal charge., A, , If uniform cross-section area, then uniform charge distribution, and uniform charge density, , 𝜎𝐵 = 𝜎𝐴, , B, , A, , B, , If non uniform cross-section area, Then non uniform charge distribution, And non uniform charge density, 1, 𝜎∝, 𝐵, 𝐴, 𝑅, , 𝜎 >𝜎, , Method Guru - Shashtrinagar, Sultanpur (UP) Mob. 7014344748
Page 6 :
Electric charge and field, , Batch -PARAKRAM, ❑ Coulomb’s Law, , The force of attraction or repulsion between two stationary point charges isq1, , F=, , q2, r, , ➢ In C.G.S. (for free space ), , k = 1,, , F=, , 0 =, , Q1 Q 2, r, , 2, , Dyne, , kQ1 Q2, r2, , ➢ In S.I. (for free space ), k=, , 1, 4 0, , = 9 109, , F=, , QQ, 1, . 12 2, 4 0, r, , Absolute permittivity of air or free space = 8.85 10 −12, , ➢ Effect of medium, ➢ When a dielectric medium is, completely filled, , Fmedium =, , N -m 2, C2, , Fair, Q Q, 1, =, . 12 2, K, 4 0 K, r, , C2, N − m2, , ➢ When a dielectric medium is, partially filled, , F=, , Q1 Q 2, 1, 4 0 (r − t + t K ) 2, , (force between two charges decreases by a factor of K), , K- Dielectric constant or specific inductive capacity or relative permittivity(r, ➢ Vector form of coulomb’s law, , ), , Q1 Q 2, , Q Q, r 12 = K. 1 2 2 rˆ12 , = −𝐹2, 1, r3, r, (Force on both charges will be equal and in opposite direction), F, , 12, , = K., , ✓ Coulomb's law is applicable to point charges only. But it can be applied for, distributed charges also, ✓ This law is valid only for stationary charges and cannot be applied for moving, charges., ✓ This law is valid only if the distance between two charges is not less than 10–, 15 m., ✓ Electric force between two charges not depends on neighboring charges, ✓ For a three charge system it is not possible that all charges are in stable equilibrium., ✓ A charged body may attract an uncharged body in specific conditions due to, induction., , Method Guru - Shashtrinagar, Sultanpur (UP) Mob. 7014344748
Page 7 :
Batch -PARAKRAM, , Electric charge and field, , Principle of superposition Net force on Q will be-, , F net = F 1 + F 2 + .... + F n−1 + F n, , ➢ If two charges applying force on third charge then magnitude of the, resultant of two electric forces is given by -, , Fnet = F12 + F22 + 2F1F2 cos , , ✓ Electrostatic force is conservative and central force, work done by, electrostatic force does not depends on path., ❑ Electrical Field:, Space around a charge in which another charged particle experiences a force, , ➢ Electric field intensity, Force experienced by a unit positive charge placed in an electric, field at a point is called electric field intensity at that point. It is also known, as electric field simply, , E = Lim, , q0 →0, , , F, q0, , , , F, E=, q0, , ➢ Unit, S.I. unit, , Newton, volt, Joule, =, =, coulomb meter coulomb meter, , C.G.S. unit – Dyne/stat coulomb., , ➢ This is a vector quantity and its direction is the same as force on the positive, test charge., , ➢ Direction of electric field due to positive charge is away from charge, while direction of electric field due to negative charge is towards the, charge, , Method Guru - Shashtrinagar, Sultanpur (UP) Mob. 7014344748
Page 8 :
Electric charge and field, , Batch -PARAKRAM, ➢ Electric field due to a point charge is, E=k, , Q, r, , 2, , , 1, k =, , 4 0, , , , Q, or E = k 2 rˆ, r, , , , , , , ➢ Electric field due to Charged arc at center, , ++, , ++, , ++, , R, , ++ ++ ++ ++, , , , 2 k , sin , R, 2, , EP =, , P, , +, , ++, , ➢ Electric field due to charged circular ring, x >> R, , kQx, E= 2, ,, (x + R 2 )3 / 2, , x << R, , kQ, x2, kqx, EP = 3, R, , EP =, , ✓ At center x = 0 so Ecentre = 0, ✓ At, , x=, , R, , 2, , E max =, , Q, 6 3 0 a 2, , ➢ Electric field and potential due to a charged straight conducting wire of, length l and charge density , Ex =, , k, (sin + sin ), r, , Ey =, , 𝐸𝑛𝑒𝑡 =, , ✓, , k, (cos − cos ), r, , 𝐸𝑥2 + 𝐸𝑦2, , If point P lies at perpendicular bisector of wire ( = ) E x =, , ✓ If wire is infinitely long i.e. l → so = =, , , , Ex =, , 2, , 2k, sin , r, , 2k, r, , Ey = 0, , Ey = 0, , , ✓ If point P lies near one end of infinitely long wire i.e. = 0, and = 2, | E x|=| E y|=, , k, r, , Enet = Ex2 + Ey2 =, , 2 k, r, , Method Guru - Shashtrinagar, Sultanpur (UP) Mob. 7014344748
Page 9 :
Electric charge and field, , Batch -PARAKRAM, , ➢ Electric field due to charged Conducting sphere or shell, Q = A = 4 R2, , Eout =, , 1, Q R 2, ., =, 4 0 r 2 0 r 2, , 1, Q, , ., =, 4 0 R 2 0, , Es =, , Ein = 0, , ➢ Electric field due to uniformly charged non-conducting sphere, , =, , E out =, , Eout, , 1, Q, ., 4 0 r 2, , R 3, =, 3 0 r 2, , Es =, , R, 1, Q, ., =, 4 0 R 2 3 0, , Ein =, , 1, Qr, ., 4 0 R 3, , =, , Q, 4, R 3, 3, , r, 3 0, , ➢ Electric field due to infinite thin plane sheet of charge, 𝐸, , E=, (E r o ), 2 0, ✓, , , 4 0, , 𝑟, , 𝜎, , Electric field near the surface of charged sheet does not depends on distance, , ➢ Electric field due to, hemispherical charged body, E=, , 𝐸, , ➢ Electric field due to, uniformly charged disc, E=, , , 1 −, 2 0 , , , , x, , x 2 + R 2 , , ~ , If x → 0, E – 2, , 0, , ➢ Electric field at all points inside, ➢ Electric field at the surface of, charged conductor of any shape charged conductor of any shape 𝐸=, , 𝜎, 𝜀0, , 𝐸=0, , Method Guru - Shashtrinagar, Sultanpur (UP) Mob. 7014344748
Page 10 :
Electric charge and field, , Batch -PARAKRAM, , ❑ Electric lines of forces, An electric line of force is that imaginary smooth curve drawn in an, electric field along which a free isolated unit positive charge moves., properties:✓ Imaginary, ✓ Can never cross each other, ✓ Can never be closed loops, ✓ Field lines are always normal to conducting surface, ✓ Field lines do not exist inside a conductor., ✓ Tangent to the field line at any point gives the direction of the field at that, point, ✓ Density of field lines is proportional to the strength of the electric field., , ❑ Motion of Charge Particle in Electric Field, (1) When charged particle initially at rest is placed in the uniform field, , (Path will be straight line), , Force, F = QE, , Acceleration, a=, , Velocity after time t, , F QE, =, m, m, , v=, , QEt, m, , Momentum, p = m, , QEt, = QEt, m, , 2, , Kinetic energy, , K=, , 1, 1 QEt , Q2 E 2t 2, mv 2 = m, =, 2, 2 m , 2m, , (2) When a charged particle enters with an initial velocity at right angle to the uniform field, , (Path will be parabolic), Uniform velocity along x-axis, , Velocity at any instant, , QEt, m, Equation of trajectory, Q 2 E 2t 2, 2, 2, 2, 2, v, =, |, v, |, =, v, +, v, =, u, +, x, y, 1 QE x , m2, y= , , 2 m u , vy QEt, tan =, =, vx, mu, , x = ut, , vx = u, , vy =, , Method Guru - Shashtrinagar, Sultanpur (UP) Mob. 7014344748
Page 11 :
Electric charge and field, , Batch -PARAKRAM, ❑ Equilibrium of Charges, , ✓ A charge is said to be in equilibrium, if net force acting on it is zero, ✓ A system of charges is said to be in equilibrium if each charge is separately in equilibrium, ✓ A body will be in equilibrium if net force and torque is zero., , Stable equilibrium, , Unstable equilibrium, , After displacing body returns back, , U is minimum, , U is Maximum, d 2U, , 2, , d U, , = +ve, , dx 2, , dx, , 2, , = -ve, , System of three collinear charge, , ➢, , Neutral equilibrium, , After displacing body never returns back, , charge Q will be in equilibrium if and only if, , |Force applied by charge Q1| = |Force applied by charge Q2 |, , After displacing body neither, come back nor move, , U is constant, d 2U, dx 2, , =0, , ✓ If all the three charges (Q1, Q and Q2) are, similar, Q will be in stable equilibrium along the, joining line but unstable equilibrium, perpendicular to the joining line., ✓ If extreme charges are similar while charge Q, is of different nature so Q will be in unstable, equilibrium along the joining line but stable, equilibrium perpendicular the joining line., , ❑ Neutral Point (A neutral point is a point where resultant electrical field is zero), (1) Neutral point Due to a system of two like point charge, At point N- |E.F. due to Q1| = |E.F. due to Q2|, , 1, Q, 1, Q, . 1 =, . 2, 4 0 x12 4 0 x 22, , Shortcut, , x, , x1 =, , Q2 / Q1 + 1, , x2 =, , x, Q1 / Q2 + 1, , Q1 x1 , = , Q2 x 2 , , 2, , (2) Neutral point due to a system of two unlike point charge, , Q1 Q2, , l=, , x, , ( Q /Q − 1), 2, , ✓ Here neutral point lies outside the line joining two, unlike charges and also it lies nearer to charge, which is smaller in magnitude., , 1, , Method Guru - Shashtrinagar, Sultanpur (UP) Mob. 7014344748
Page 12 :
Electric charge and field, , Batch -PARAKRAM, , ❑ Time Period of Oscillation of a Charged Body, ➢ Simple pendulum, , ✓ Electric field downwards, l, g, , T = 2, , T2 = 2, , l, g + (QE/m ), , T2 < T, ✓ Electric field upwards, T3 = 2π, , ✓ Electric field in Horizontal, l, g − (QE/m ), , T = 2, , l, , (g, , 2, , + (QE/m ) 2, , ), , 1, 2, , T3 > T, ✓ If mg = QE then T will be infinite, ➢ Charged ring, , ➢ Spring mass system, T = 2, , T = 2π, , m, k, , 4 0mR 3, Qq, , ➢ Charge particle oscillates between two fixed charge Q of same nature, Case I - If all the three charges are similar, q, will execute SHM along the joining line, , Case II –If center charge is in opposite nature, q, will execute SHM perpendicular the joining line, , 2d, , 2d, Q, , Q, , Q, , (+q , m), , 𝑇 = 2𝜋, , 𝜋𝜀0 𝑚𝑑 3, 𝑄𝑞, , Q, (-q , m), , 𝑇 = 2𝜋, , 2𝜋𝜀0 𝑚𝑑 3, 𝑄𝑞, , Method Guru - Shashtrinagar, Sultanpur (UP) Mob. 7014344748
Page 13 :
Electric charge and field, , Batch -PARAKRAM, ❑ Electric Dipole, , System of two equal and opposite charges separated by a small fixed distance is called a dipole, Ee =, , 1, p, ., 4 0 r 3, , Eg =, , 1, p, ., (3 cos 2 + 1), 4 0 r 3, , Ea =, , 1, 2p, ., 4 0 r 3, , ➢ Dipole moment, It is defined as the product of the magnitude of either of the charge and the dipole length, , , , p = q (2 l ), ✓, , ✓, , Its S.I. unit is coulomb-meter or Debye and C.G.S unit is stat Coulomb-cm, 1 Debye = 3.3 × 10–30 C m, , It is a vector quantity directed always from negative charge to positive charge, , ❑ Electric Dipole in an uniform electric field, ➢ Net force = 0, ➢ Torque = pE sin , , ➢ Work done in rotation, , W = pE(cos1 − cos 2 ), , ➢ Potential energy of dipole, , U = − pE cos , , 𝜏Ԧ = 𝑃 × 𝐸, , ➢ Oscillation of dipole, , =, , 0o, , Stable equilibrium, , =, , 90O, , Not in equilibrium, , =, , T = 2, , 180o, , Unstable equilibrium, , =0, , max = pE, , =0, , W=0, , W = pE, , Wmax = 2pE, , Umin = – pE, , U=0, , I, pE, , ➢ Motion of dipole will be, pure rotational, , Umax = pE, , ➢ Electric dipole in non-uniform electric field➢ Net force on dipole, , ⅆ𝐸, ⅆ𝑟, ➢ Motion of the dipole is combination of translatory, and rotatory ., 𝐹 = −𝑃, , Method Guru - Shashtrinagar, Sultanpur (UP) Mob. 7014344748
Page 15 :
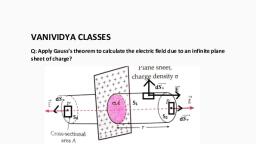
Electric charge and field, , Batch - PARAKRAM, ❑ Electric Flux, , It is defined as the total number of lines of force passing perpendicular through, a surface placed in the filed., ✓, , In case of variable electric field or curved area, , = E. A, , =, , = E.A cos, , E. dA, , ❑ where 𝜃 = angle between electric field and area vector, ✓ Unit : (a), ✓, , N-m2/C, , (b) volt - meter, , Flux entering is taken as negative while flux leaving is taken as positive, , 𝐀, , 𝑬, , 𝐀, θ = 00, , θ = 90, , 𝝓 = 𝑬𝑨, , 𝝓=𝟎, , 𝑬, , 𝑬, , 𝑬, , 𝐀, 𝝓 = 𝑬𝑨 𝐜𝐨𝐬 𝜽, , =, , E. dA, , Electric Flux Density, It is defined as the total number of lines of force passing perpendicular through, per unit area a surface placed in the filed., , 𝜙, = 𝐵 = Electric flux density/ Electric field intensity, 𝐴, , ❑ Gauss's LawThis law states that electric flux through any closed surface is equal to, , 1/o times the net charge 'q' enclosed by the surface ., , 𝜙 𝑇 = ර𝐸 ⋅ 𝑑Ԧ =, , 𝑞𝑖𝑛, 𝜀0, , ✓ The electric field is resulting from all charge, both those inside and those outside the Gaussian surface, but electric field due to a charge outside the Gaussian surface contributes zero net flux through the, surface., ✓ The closed surface can be hypothetical and then it is called a Gaussian surface., ✓ Net flux is independent of distances between charges inside the surface and their distribution., , ✓ Net flux is independent of shape , size and nature of surface., ✓ Net flux depends on charges enclosed by surface, their nature and on the medium., , Method Guru - Shashtrinagar, Sultanpur (UP) Mob. 7014344748
Page 16 :
Electric charge and field, , Batch -PARAKRAM, ✓, ✓, ✓, , Net flux due to a charge outside the surface will be zero., If ∆Q = 0 , then , 𝝓 = 0 but it is not necessary that E = 0, Gauss law is valid only for the vector fields which obey inverse square law, , ✓ If a closed body (not enclosing any charge) is placed in an electric field, (either uniform or non-uniform) total flux linked with it will be zero, , Examples of calculating net flux using Gauss’s law, 𝑄, , Flux from surface S1 𝜙1 = + 𝜀0, , 1., , Flux from surface S2 𝜙2 = −, , 2., , Flux from surface S3, , 𝜙3 = 0, , Flux from surface S4, , 𝜙4 = 0, , 𝑄, 𝜀0, , Flux 𝑡ℎ𝑟𝑜𝑢𝑔ℎ 𝑠𝑢𝑟𝑓𝑎𝑐𝑒 𝑎 (𝜙𝑎) = Flux trough surface b(𝜙𝑏), , a, , 2𝒒, , 𝜙𝑎 = 𝜙𝑏 =, , b, , 3., total =, , 4., , 1, , 0, , 2𝑞, 𝜀0, , .(Q), , face =, , Q, 6 0, , Flux leaving from curved surface = + 𝐸 × 𝜋𝑅 2, Flux entering flux from flat surface = - 𝐸 × 𝜋𝑅 2, R, , Total electric flux= 0, , 5., Flux leaving from curved surface (Outside) = 𝐸 × 2𝜋𝑅 2, , Flux leaving from curved surface (Inside) = - 𝐸 × 2𝜋𝑅 2, , Method Guru - Shashtrinagar, Sultanpur (UP) Mob. 7014344748
Page 17 :
Batch -PARAKRAM, , Electric charge and field, , q is placed at center of hemisphere, , q is placed at one end of cylinder, , q is placed at the center of, one face of a cube, , q is placed at the corner of, a cube, , face =, , Q / 8 0, Q, =, 3, 24 0, , q is placed at the middle of, one edge of a cube, , (Flux from 5 face only), , (Flux from 3 face only), cube, , (Flux from 4 face only), cube, , Method Guru - Shashtrinagar, Sultanpur (UP) Mob. 7014344748