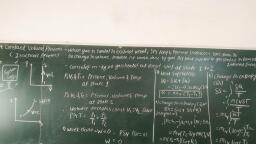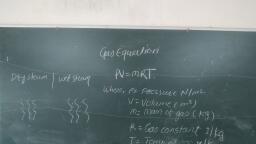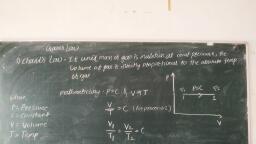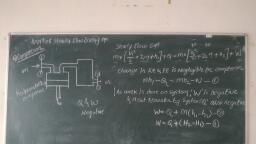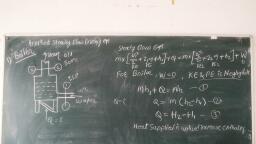Page 1 :
Ideal Gases and Ideal Gas, Processes, , , , 2.1, , , , , , [Weightage of Marks = 14, Teaching Hours = os}, , Avogadro's law, Calculate molar volume. Derivation of characteristic gas equation using Boyle's, and Charle's law, characteristic gas constant and Universal gas constant., , 2.2 Ideal gas processes — Isobaric, Isochoric, Isothermal, Isentropic, Polytropic, Throttling and their, , representation on P-V and T-S diagrams. Determination of work, Heat, Internal energy, Enthalpy, change and Entropy change., , About this Chapter, , After reading this chapter, students can —, , Evaluate the work done and thermal energy transfer according to Boyles law for the given situation., Evaluate the work done and thermal energy transfer according to Charle's law for the given situation., Calculate the mass of a gas and its final condition parameters after undergoing Polytropic process for, the given situation., , Determine characteristic gas constant of commonly used gases for the given data., , Calculate different energy changes during ideal gas processes for the given situation., , , , , , , , , A perfect gas or an ideal gas is one, which follows the gas laws at all ranges of pressure and, , temperatures., , An ideal gas has no forces of molecular attraction because at low pressure and high, temperature, molecules of gas are far away from each other and so there is no any, molecular attraction between them., , In nature, no such gas exists but real gases follow these laws at low pressure and high, , temperature or at both., , , , 2.1.1 Assumptions Made for Ideal Gas, , 1., 2., , 3., 4., As, , , , A finite volume of gas contains large number of molecules., The collision of molecules with one another and with the walls of the’container is perfectly, elastic., The molecules are separated by large distances compared to their own dimensions., The molecules do not exert forces on one another except when they collide., long as the above assumptions are valid, the behaviour of a real gas approaches closely that, , of an ideal gas., , [2.1], , Scanned with CamScanner

Page 2 :
— — — ———————, , Gases and Ideal Gas Processes, , Tremelengnesng a, , , , , , , , , , , , , , , , , , at constant pressure, the volume», , f the gas’., P,, , , , Charie’s law states that ‘If unit mass of gas Is maintained, Of gas is directly proportional to the absolute temperature ©, , It can be shown on PV diagram as —, Mathematically, V « T, ifP=C, , , , o ¥ Ze, , +. For process 1-2, pw, , : ve, , oe Vic, , “ Ma Ne Fig. 2.1: Charle’s law, Ti ~~ Ta, , * Charle’s law can also be stated as, ‘If unit mass of gas is maintained at constant volume,, the pressure of gas Is directly proportional to the absolute temperature of the gas’., Mathematically,, Pe T,ifV=C, , Boyle's gas law states that ‘If unit, mass of gas is maintained at constant, temperature, the volume of gas is, inversely | proportional with the, absolute pressure during change’ of, : -State of gas'.. vee ot, , tt can be shown in PV diagram as —, , , , , , , : Mathematically, 0, 1., , V« P if T=C . : Fig. 2.2: Boyle's law, s ose seee PY e, , :. For process 1-2, — Pec, , a . » Pi = P22 0, , ° ws tg Ww, ” ’ P, ~ Vy 20, , , , , , , stern, :, . GER Cae, , A mole of substance has a mass numerically equal to the molecular weight of the substance., For example, 1 gm mole of oxygen has a mass of 32 gm and 1 gm mole of carbon dloiide, has a mass of 44 gm and so on. ;, , e Fora certain gas, m = Mass In kg, , M = Molecular weight in kg/kg-mole, , Then, number of kg-moles of the gas (n) Is given by,, , mk = Dkg-mol, N= M(kg/kg-mole) = mM “9-Moles, , ae, , I, , Scanned with CamScanner

Page 3 :
Thermal Engineering 2.3 Ideal Gases and Ideal Gas Processes, , © The molar volume, Vmoie= ¥ m3/kg-mole, , Where, V = Total volume of gas In m?, , ¢ There are 6.02 x 1026 molecules in a kg-mole of a substance. This Is known as Avogadro’s, number (A). If N = Total number of molecules. Then, N = nA., , ¢ Avogadro's law states that ‘equal volume of all the perfect gases at the same temperature, and pressure contain an equal number of molecules’., , ¢ Thus, if two Ideal gases having masses ma and mp having molecular weight Ma and Ms, respectively, are contained In two vessels of equal volume at same temperature and, pressure, then each gas will contain the same number of molecules (N)., , ¢ Mathematically, ma = NM, = a Ma, N, and Mp = 0Mg = A Ms, Mm, _ Ma, ms: Mp, But m = pV, where V is same for both gases A and B., paxV Ma, paxV ~ Mp, Pa _ Ma, Pa Mp, But p = 1/v We, Ye _ Ma, Va Mp, , MaVa = MaVe = Vote = Constant A ;, e The product of molecular weight and specific volume is constant for. all gases at same, temperature and pressure and is known as molar volume. _. ee tone, ¢ Thus, from Avogadro's law, ‘The volume of 1 kg- -mole of all gases at normal temperature, and pressure is the same’ and is equal to 22.4 m’., , , , , , , , , , Consider 1 kg of gas which changes its, state from P,, V1, Ti to P2, V2, T2 by two, processes namely constant pressure, process (1 to A) and _ constant, temperature process (A to 2) as shown in, Fig. 2.3., , * During constant pressure process,, , volume changes from V; to Va and during, constant temperature process volume Fig. 2.3: Derivation of characteristic gas, , changes from Va to V2. equation, , Process 1-A, P = C Applying Charle’s law we get,, , Mi _ Ma, , , Ti (Ta, Mi Ma ® =T], o Va = 7, TA= Ty Ta Ai oy ae (2.1) [AS Ta = Ta], , Process A-2 , T = C. Applying Boyle’s law we get,, VaPa = V2P2, , Scanned with CamScanner

Page 4 :
2.4, , P; Po, Va = Vip, = V2p,, . From equation (2.1) and (2.2), We get., , Mw — vi, Ty te = Map, , 7 _.. Characteristi, n J/kg K, , , , , , mRT n, = Characteristic gas constant i, Pressure in N/m?, , Volume in m?, , Mass of gas in kg, ire of gas in K, , «For gas having m kg mass,, Where,, , u, , 43 <0, i, , , , , , , , , , , CHAR: GAS CON, Characteristic gas equation is, PV = mRT. ;, Where, R = Characteristic gas constant, Unit of Characteristic gas constant is J/kg K., , The value of this constant is different for different gases., for Oxygen., , on, * different for different gases., , ¢ For uniformity, characteristic gas constant is replaced by Universal gas constant, which is, product of molecular weight and characteristic gas constant. ., , , , , , , , Let, M = Molecular weight of gas in kg., R = Characteristic gas constant for same gas., Then, R = Characteristic gas constant x Molecular weight = R M, , Unit of Universal gas constant is J/kg-mole K, , , , , , , , , , , , , , , 2.9.1 Isobaric Process (Constant Pressure Process), , , , e For isobaric process, consider perfect gas heated in frictionless piston and cylinder arranyenionl, as shown in Fig. 2.4. ., , TA, , , , , , =, , , , , , , , , , (a) (b), Fig. 2.4: Isobaric process (constant Pressure), , , , , , Scanned with CamScanner