Page 1 :
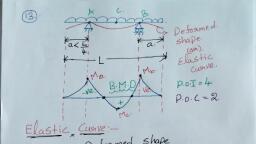
Chapter, , 4:, , :, , Bending Momenis, , shown in Fig. 4.33 (b)., shall be as, B.M., diagram, and, Shall be zero, in Fig. 4.33, Ifa /2 then Mnar, shall be as shown, diagram, B.M., and, be negative, Ifa> U2 then Mma Shall, at a distance x from either end theCn, If B.M. is zero, , (c)., , =, , +, , +, or,, , w +2a)(N-a)= (0, , 2a) t - d, , =, , THE POINTS OF CONTRAFL.EXURE, of beams in oppositee, nature always produce curvatures, The bending moments of opposite, the point itself having ze, the bending moment changes sign at a point,, is, directions. In a beam, moment and this point, curvature at this point of zero bending, momeni, the bcam changes, , 4.19., bending, , called the, , in opposite direction., contraflexure. So at a point of contraflexure the beam flexes, of, point, , contraflexure, is called the point ofinflexion o r a virtual hinge. The point of, point of contratlexure, a span, the bending moment equation in terms ofx equal t0 zero for part of, can be found by setting, to change sign., where bending moment is likely, , The, , Overhanging Beams:, , Example, , Draw S.F. and B.M. diagrams for the loaded beamn, , 4.14., , shown in, , Fig., , 4.34, , (a)., , Solution. To determine reactions R and R, taking moments about A, we get, , +14 = 50, R x5=5.5 x2 +2x5x+ 2x7=11+25, , 5.5 kN, , R=10kN, kN, But R,+R =5.5 + 2 x5 +2= 17.5, , R, , 175, , =, , 10, , -, , 7.5 kN, , =, , QC, , S.F. calculations:, Sp-B - 2 kN, , 2, , 1, , =, , -, , m, , =, , -, , m, -2 m, , 3 m-, , R, , (a) Beam, , -, , D, , AB, 1.5, , m-, , Sp = - 2 + 10 =8 kN, 3.5 kN RA =7.5 kN, Sc 8 2x3 5.5, 7.5 kN, SA -3.5 2x2, =, , 2 kN, , 2 kN/m, , 10 kN, 8, , -, , kN, , S.F. diagram is shown in Fig. 4.34 (b)., 2, , B.M. calculations:, , (, , Mp=0, , 2 - 4 kNNm, B.M. mid way between B and C,, , M-2 x, , Mp, , =, , -, , =, , 2x 3.5, , +, , 2 kN, , 3.5 kN, , 10 x 1.5 -2, , 7.5 kN, , 2 kN, , (b) S.F. diagram, II kNm, , 6.5 kNm, , X1.5x, , 5.75 kNmn, , =-7+15 -2.25 =5.75 kNm, , Mc = - 2x5 + 10x3 -2x3x3/2, , r = 0.54m, , 10 + 30 -9 = 1IkNm, , B.M. mid way between A and C,, , Mo, , 2x 4x 4/2, , 2x6+ 10x 4, , -, , = -, , 12 + 40, , 16 -, , 5.5, , -, , 6.5 kNm, , 5.5 xI, , 4 kNm, (c) B.M. diagram, , Fig. 4.34, Mo =+ 7.5 x 1 - 2x 1x, , or,, =, , 6.5 kNm, , ..., , 2, From left side, , |

Page 2 :
Grinding machine., Since B.M. at B is negative and at P+ ve. therefore. the B.M. will cross zero line betweenthen, Let the point ofcontraflexure lie at a distance, , M, =-2 (2 +x), , from B., , Or,, , 10x - 2 xIx/2 = 0, - 4- 21 + 1 0 =0, , Or,, , -4 +St -, , +, , = 0 or, , - 8x + 4 0, , 8t 6 4 - 16, , 8t 6.93, , Of,, from which * = 0.54 m, the other value of r being inadmissible., , B.M. diagram is shown in Fig. 4.34 (c)., , Example, , 4.15., , Fig. 4.35 (a) shows, , loaded beam. (a) Sketch the B.M. and S.E, diagun, giving the important numerical values. (b) Calculate the maximum bending moment and the pou, a, , which it occurs., , Solution. To deternmine reaction, , R,, , and, , R, taking moments about A,, , RX 4.5 =6 x1.5 +3x3+3x 4.5 x, =, , R, , But, R+, , 9 +9 + 30.375, 13.8 kN, , +, , 4.5, , 13.8, , R, , =6+3+3 x4.5 +2 24.5 kN, 24.5- 13.8 10.7 kN, S.F. calculations:, , RA=, , =, , E-B-2 kN, S, , = - 2 + 13.8, , Sp = 11.8 -, , 11.8 kN, , 3 x 1.5 - 3 =, , 4.3 kN, , Sc = 4.3- 3 x1.5 - 6 = -6.2 kN, , SA-6.2 -3x1.5 = - 10.7 kN, , +2x, , (4.5+ 2.4), , we, , get

Page 3 :
Chapter, , : 4, , : Bending, , Moments and Shearing, 6 kN, , the point between C and D, To locate, is zero we have from similar, where S.F., abc and cde., triangles, , 0.2, , 3 kN/m, , AB, , D, , C, , 1.5m1.5m->+1.5m-, , cd, , (a) Beam, , cd, , 11.8 kN, , 0.2 cd= 4.3 (1.5 - cd), or., , or, , 0.2 cd, , 7.3 kN, , 6.45 -4.3 cd, , 4.3 k N e, , cd= 1.43 m, , or, , At this, , a CA, , will be maximum., , point B.M., , TTTT, , -2, , x, , 2, , x, , =-, , d, , 143m, , ME = 0, , Mp, , =, , 1.5, 2, , 10.7 kN, , (b) S.F. diagram, , 12.612.61, , =-7.8+ 20.7-3.375, = 9.52 kNm, , 9.52 kNm, , -2 x (2.4 +1.5+1.43) +, x, , (1.5 +, , 1.43) -, , 3 x, , 13.8, , 2.93, , 0.43, , 2.93, 3 x 1.43, = - 10.66 + 40.43 -12.87, , 4.8 kNm, (c) B.M. diagram, , Mc =-2 x 5.4 + 13.8 x 3 - 3x 1.5 -3x 3x, 10.8 + 41.4, , m, , 4.29, , = 12.61 kNm, , = -, , 2 kN, , 2 kN, , 6.2 kN, , - 4.8 kNm, (2.4 +1.5) +13.8, , 2.4, , x 1.5 -3 x 1.5 x, , M, , *, , b0.2 kN, , B.M. calculations:, , M, , -2.4 m, , R13.8 kN, , RA 10.7 kN, , 4.3, , (1.5- cd), , 2 kN, , 3 kN, , E, , ab_de, ac, , orce, , 4.5 -, , Fig. 4.35, , 13.5 = 12.6 kNm., , MA = 0, , Since B.M. at B is negative and at Dis positive, therefore, the B.M. will cross zero line between, them. Let the point of contraflexure lie at a distance x from B., , M, = -2x(2.4+ x)+ 13.8x x - 3xxx, , =0, , Or,, , -4.8 2 x + 13.8x -1.5r = 0, , or,, , 1.5x 11.8x + 4.8 =0, , from which x = 043 m, the other value of x being inadmissible., B.M. diagram is shown in Fig. 4.35 (c)., , Example 4.16. For the beam loaded as shown in Fig. 4.36 (a) calculate the value of U.D.L. w, at C is 50 kNm. Draw the S.F. and B.M., diagrams for this beam for the calculated value, of w. Locate the, point of contraflexure, if any., Solution. Taking moments about A, we get, , So, , that B.M., , RX 8 = w x4x4/2 +20 x 10 =8w + 200, or, , Rg (W+ 25) kN, But, R, +R =Wx 4 +20, R= (4w+ 20) - (w+ 25), = (3w-5)) kN