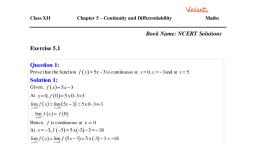Page 1 :
Scanned by CamScanner, 9. APPlications. of Integration 2) Find an approximate value 3 Find an approximate value of Ex9.1, EXERCISE 9.1., 0.5, |-5, 1) Eind an approximate Value, of Jx2dx by applying the, (2-x)dx by applying the mid-Raint Estimate the value of fx, 1.5, of, Jxdx by applying the left-en yight -end rule with the Pantil rule with the pantition{1-1,1•2, | using the Riemann Sums coes, 1-3, 1-4,1-5}, -Ponding to sub intervals of, equal width and applying, ci) left-end rule (ii) sight-end, Yule (iii) the mid- Point Yule, Soln:, (i) a=0, b=0:5 and n=5., -tion {い,-2,1-3,14ット5 Soln:, Soln:, Yube with the partition {1-1,1-2,1-3|, 1-4, I-5}, Sola:, a=1, b= 1.5 and n= 5, aニリb=lg and n=5, a=!, b=1.5 and n=5, 0.1, 4X = b-a, in, ax = ba = 5- =, AX =, n, 1.5-1, %3D, 1.5-1, 0.1, b-a, 1.5-1, 5, AX =, Ax =0.1, AX =0.1, Let xo =1, X; =l·1, X2=\•2,, Ax = 0:), Let xo=し X」=l1, Zュ=1-2| Let xi=l), X2=l,2,X3=1-3,| xg=l-3,ス4ニ-4 and X5=1-5, X3 = 1•3, X4=1-4 and X5=1-5 X4 =1.4 and X5 = 1.5, 0.5-0, Ax = b-a, AX =0.1, Let fex) = 2-X, Let Xo =0, x1=0.1, X2=0.2, Let Fcx)=x., Let fox) =x?, S=, X3-0-3, 24 =o.4 and x5=0-5, S= [fcx0)+f(a1)+fras)4., +F(xn-1)JAx, S= [fixo)+f(x)+fra2), S=[f(1·1)+f(1•2)+ f(l-3)+f(1-4), + F(!-5)]co-1), s=[f(l.05)+ f(1-15)+f(1.25), +f(1:35)+f(1.45)](o•1), = [0.95+0.85+0.75+0.65, +0.55](0.1), Sz[f1)+fC1-)+fC1-2)+f(l:3), +f(l·4)](0.1), s= [fto)+f(o-1)+flo.2)+ F(0-3), +f(o.4)](0•1), =[1-21 + 1. 44 +l.69+1-96+2:25/(01), ニ, - 8.55x0.1=0.855, = 6xo.1 =0.6, j.5, =0•30X0•1=0.03, 0.5, ニ, 3.15×0-1こ0·375, :. Jxdx=0.6, .. x*dx =0.855, x?dx =0.03, 1.5, S(2-x)dx3Do•375