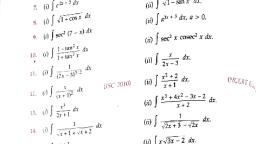Page 1 :
INTEGRATION BY SUBSTITUTIONS, 1. INTEGRATION BY SUBSTITUTION:, Such functions in which standard formulae can not be applied directly but by making some proper, substitution they are changed in standard functions and their integrations can be done using the, , formulae of standard functions. This method of integration is called Integration by Substitution., The method is made clear below taking various forms of such functions., TYPE I, , (1) FUNCTIONS OF THE FORM | f (axt b) dr, Let ax tb =t, then differentiating (ax1t0) dr= dt d s =, , dt, a, , saxt b)d=Js)x, , ., , Js(ax t, , b), , =, , =, , F)= F(ax+b), a, , (axt b)+, , F, , a, , (Formula), , From the result it is clear that formulae of the standard functions can be applied directly till the, variable is linear function of x the rule given below., , Rule: In the funetions of the form f(axt b), apply the formulae of the standard functions, directly taking (ax t b) as x and then divide the result so obtained by the coefficient of x. Thus, according to this rule,, , (ar t, , de=, , ar t b)"*, , +C, , (n +1) a, , (ax t b), , dy=log, , (ii), ii), , b)", , C, , a, , cos (axt, , b), , dr=, , sin (ax t b), , 4C, , a, , eaxt b), , (iv), , Jeadr-, , For example:, , 1., , +C etc., , (8x+3)°, (8x+3) dr = (8*5=, 6x 8, 48, , 2.7-3, , dr, , =, , 8, , (7X- 3), , Ans., , Ans., , 7, , TYPE II, , (2) FUNCTIONS OF THE, , FORM|f (x)}" f'(x) dx:, ., , If the integrand is the product of two such functions that one function is the differential coefficient of, the other function, then

Page 2 :
8, , ---~-a., , Sx) =t, , put, , and f ' (x) dx = dt, , IS " s ' ()dr =[" dt, , then,, , For example:, put, , Then, , sec x tan*x dx, tan x, , =, , t, , t'_Lf (x)]"*i, , =, , +, , C, , n +1, , n+1, , sec x is the differential coefficient of tan x,, see, , and, , x dr =, , Formula, , dt, , tan, , sec x tanx dx =f12 dt =, =, , C, , +, , Ans, , 3, , 3, , f' (x), dx:, , (3) FUNCTION OF THE FORM, , f(x), , If the intergrand is a fraction in which the numerator is the differential coefficient of the function, denominator, then put denominator equal to t', ie.,, Sx)= t, , put, , dx=[, , then, , and f ' (x) dx = dt, , =log t= log IfI, , (Formulam, , Rule Integral of the function, in which Nr. is the differential coefficient of the Dr., is equal, the, , log of, , the Dr. In, , case, , the Dr. is of the form [f (x)I" and Nr. is equal to, , f' (x),thenp, , f(x) =1, the integral will become | " dt, which will be integrable applying the formula d, , J " d., dx,, For example: sin, , put sin x = t and cos x dx = dt, , Sinx, , then, , COS x dx, sin, , dt, , x, , 2, , =, 2 sin, , 2., , -2, cosec, , At, , x, , x, , 2. TO FIND THE INTEGRALS OF THE FUNCTIONS tan, x, cot x, sec x,, , tan xdr = sin, COS, Let, , cos x = then, , -, , sin, , x, , dx, , =, , dx, , (U.P.Diploma19, , x, , dt, , tan xdx =f =, =, , cox, , s i n x dx = =, , -, , log, , log (cos x), , t, , =, , =, , log, , -, , log, , dt, cos x, , =, , log sec x + C, (Formub, , t a n x dx = log sec x + C, , (ii), Let, , cot xd, sin, , x, , =, , t, , cot x d, , COS X, , Sin x, , then, , dx, , cos x, , dx, , =, , dt, , = | = log t = log sin x + C

Page 3 :
Integration by Substitutions, , (Formula), , cot x dr = log sin x+C, , sec x(sec x+ tan x), , sec x dr=|, , (iii), Let, , sec x+ tan x, , t, then, , =, , (sec, , tan, , x, , sec x+ tan x, , sec x) dx, , +, , x, , ec x dx = |, , we have,, , sec x dx, , =, , dt, i.e.,sec x (tan, , x+ sec, , x), , dx, , =, , dt, , = log t = log (sec x + tan x), , (Formula), , = log (sec x + tan x) +C, , This result can be simplified as under, log (sec x+ tan r) =, , sin, , (1+ sin X, , COS, , cos x, , s lo, , log, cos x, , sin 2 (x/ 2)+ cos ( r / 2 ) + 2 sin (x/2) cos (r/2), E, , log, , cos, , (x/ 2), , -, , sin, , (x/ 2), , [(cos (x/2) + sin (x/ 2)]*, =, , log, , [(cos (x/ 2), , sin (x/2)][cos (x/2) + sin (x/2)]|, , 1+ tan (x/2)|, , loo cos (x/2)+ sin (x/2, , = log, , cos (x/2) -, , tan, , TT, , sin (x/ 2)|, , 1 - tan (x/2)], , X, , + tan, , = log tan|, , = log, , 1, , tan, , X, , x tan, 4, , (Formula), , sec x dx = log (sec x + tan x)= log tan, , cosecx dx, , (iv), cosec x +, , Let, , cot x, , =, , =, , [COSCC X(COSec r+, , cot, , x), , (U.P. Diploma 1998), , cosec x + cot x, , 1, then (-cosec x cot x -, , cosec x ) dx =, , dt, , cosec x (cot x + cosec x) dx = - dt, , dt, = - |=, - log t=, , cosec x d, , we have,, , cosec x dx, , =-, , log (cosecx +, , cot, , log (cosecx + cot x), , x) +C, , (Formula), , This result can be simplified as under:, -, , log (cosec x, , + cot, , x), , =, , -, , log, , - l o g t(1+Sin, Sinx, , COS, , Sin x, , = log (1+ cossx, , log, , cosec x dx, , log, , =-, , sin x, , 2 sin (x/2) cos (x2)=, 2cos, , x\, , x, , 1+ cos x), , sin x, =, , cos, , log tan, , (x/2), , log (cosec* +cot x) =log tan, , +C, , (x/2), (Formula)

Page 5 :
12, SOLUTION: Let, , 4x+3 = t,, , then (4 x 1+0) dx = dt, , dx=., , dt, , and = 3, , 4, , Jay4x+3d =f, , x, 3/2, , =, , -, , 4, , -3)x d, , 16, , 3/2, , 32 dt =, , - 3x, , 3/2, , (4x+35/2 4x+3)32+C, EXAMPLE 6. Find the value off|, , Ans., , 1, , Vx+1+x- 2, , SOLUTION: If the function is of the form-, , first rationalise the function and, , (ax + b) t (ax + c), , then apply the formulae directly or apply the method of substitution as is the case., , Rationalising the denominator,, , [x+1-Vr-2] dr, , +1+ *-2]lVx +1]-vx -2, + 1 - r + 2dr= + l - r - 2, x+1- x +2, , =-, , r+1)3/2, , 3, , x -2)3/2, , C, , +C, , (3/2), , (3/2), , 3, , dx, , a+1, , 2, , +C, , Ans., , EXAMPLE 7. Find the vaiue of| (3 x +2) V(2x +3) d., , SOLUTION: Let 2x+3 = i =x =Sdifferentiating, dr=*, , (3x+2)2 +3dr =, =, , 2ix, , 2, , S9+4, , 2, x, , 1V/2, d = (33/2 52dt, 2, , S/2, , 3/2, , (5/2), , (3/2, , +, , C, , (2x +3/2- x+332+c, 3, , Ans., , EXAMPLE 8. Evaluate l 2x+5x-7 dx, x+1, , SOLUTION, , 2*5r-7 dr, x+1, , (dividing Nr. by Dr.)

Page 8 :
sin x, , s.0, , sinx= dr, , 1+ sin x, , dx, , [Hint: Divide Nr. and Dr. by cos x], , (3 cos x -2 sin r), 5, , sin x cosx, , (U.P. Diploma 2013), , dr, , sin 2r, , 9., a, , cos x+bsinx, , (U.P. Diploma 1999), , dx, , (U.P. Diploma 2012), , (i) t a n 2 dx, , 1+r, e(1+), , cot (log ), , 10., , 1+ tan, , xe, , (iv)tanx+cotx)dr, , dx, , (v)1+2 tan r, , (vi)e, , (U.P. Diploma 2000), , cos (r e), , X, , (tan r, , +, , sin 2 x, , (vi) J, , sec x) dr, , dx, , (U.P. Diploma 2003), , sinx+ cos" x, , xe"dr, , (viii)|, , sec r, , log (secr +, , tan x) dr, , (U.P. Diploma 1996, 2001), dx, , 11., , 1-*, (ii), , (U.P. Diploma 1995), , dx, , dv2-1-2x-3, , (2x-1)/r +1 dr, , ANSWERS 2, 1. ) l o g(6 x + 4), , (i)--, , 21(7x -12), , 4, , cos x", , A, , 4, , iv)sin(2.), , 14, , i )Sin3, )-, , tan (4 x), , (i)-(cos 7 x +7 cos x), , 2. )13 sin 2x- sin 6 x], 3., , (ii), , 3, , G), ii), , + loglog(1+) Gv) log(3+4 tan x), , ()llog(x+y1+x*)?, , (vi)tane, , (vi)-log(be"* +C), , (vii)(sin, , (ix) 2 sin vx, , (x), , 2, sin r