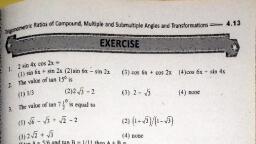Page 1 :
TRIGONOMETRY, , UNIT-II|, 3.1, , COMPOUND ANGLES, , Trigonometrical ratios:, There are six Trigonometrical ratios sine, cosine,, , tangent, cotangent,, as, , sin, , 0,, , cos, , 6,, , tan, , secant, , 6,, , cot, , and, , 8,, , cosecant, , sec, , 0 and, , The side opposite to angle, , shortly written, , cosec, , 6., , opposite to 90°, opposite, Hypotenuse. The other side is adjacent side., Hyp, Sin=Opp cosec, Cose=d, , Hyp, tan=PP, , 90, adjacent side (adj), , Fig.3.11, , IHyP, Cos&, , adj, adj, , tane, , opp, , cote=, , adj, , is called, , Opp, , Sine, , sect=, , Hyrotenuse, , (Opp), , (Theta) is called, , side. The side, , Hyp, , HYP, , Opposite side, , Note:, tan=, , Sin, , and, , cose, , Cose, , cot9 =, , sin6, , Fundamental trigonometrical identities, 1), , s i n - +cos-0 =, , 1, , 2) 1+tan 0, , sec0, , 3) 1+cot0 =cosec-80

Page 2 :
70, , Engineering Mathematics-, , Trigonometrical ratios of known angles, e, , 0, , 30, , 45, , sine0 2 2, , 60, , 90, , 2, 0, , cose, , tan 0 A, Signs of Trigonometrical ratios, 90, , Quadrant, , Quadrant, I, 90+, , 90-6, , 180-0, , 360 +0, , Quadrant, , Quadrant, IV, , 180 +0, , 270+0, , 270-0, , 360-0, , 180, , -6, , 270°, , 0 (or) 360°P

Page 3 :
Note:, -6falls in, , Quadrant, , IV where cos and, , sec, , 0are +ve. Therefore, , c o s 0 and sec (-0)=, cos(-0) =, , sec 0; sin (-0)=-sin ; tan(-0)=-tan 0; cot (-0)=-cot 6; cosec(-6)=-cosec 6., , CompoundAngles:, If an angleis expressed asthe algebraic sum or differenceof two or moreangles, thenit is called, compound angle.

Page 4 :
72EngineeringMathematics-I, , Formulae, 1) sin (A+ B) sin A cos B +cos A sin B, 2) sin (A- B) sin A cos B- cos A sin B, =, , =, , 3), , cos, , (A +B), , 4), , cos, , (A -B), , =, , =, , cos A cos B- sin A sin B, cos, , A, , cos, , B, , +, , sin A sin B, , B, 5) tan(A+ B)= 1- tan Atan, tan B, tan A+, , tan A tanB, , 6) tan(A-B)=, Results:, 1., , I+tanA tan B, , sin (A +B) sin (A- B) = sin?A - sin?B, , sinB+cos, B, cos B =, =, , sin A, , 1 - sin'B, , =cos A = 1, cosA =, , 2, , 1, , 1 -, , sin>A, , cos (A+B) cos (A - B) = cos'B - sin'A= cos A - sin'B., , sin?A +cos?A =I, cosA =1-sin A, sinB cos*B =1, =, , sin B, , = I - cos*B, , Sin'B +cos-B = 1, , sin A, , =, , cos B, cos A, , =, , 1, , =, , 1, , -, , sin B, , sin A = 1 - cos?A

Page 5 :
Trigonometry, , 3.1 WORKED EXAMPLES, , PART-A, 1., , Find the value, , of sin65° cos 25° +, , cos, , 65° sin 25°., , Solution:, sin65° cos 250 + cos 65° sin 250, , sin (A + B) formula, , sin (65° + 2 5 ) = sin 90°= 1, , 2., , Find the value, , of sin 40° cos, , 10°-, , cos, , 40° sin 10°., , Solution:, sin 40°, , cos, , 10°-, , cos, , 40° sin 10°, , sin" (A - B), , sin (40°-10°) = sin 30°, 3., , Find the value, , of cos 50° cos 40°, , formula, , sin 50° sin 40°., , Solution:, cos, , 50°, , cos, , 40°-sin, , cos ( 5 0 ° + 40°) =, , 4., , 50° sin 40°, , cos 90° =, , cos (A -B) formula, , 0, , What is the value of cos 70° cos 10°, , +, , sin 70° sin 10°?, , Solution:, cos 70° cos 10° + sin 70° sin 10°, cos, , (70°- 10°) = cos 60°=, , cos (A +B) formula, , 1, 2, , 5., 5., , an z0" + tan, , Find, value of, Find the value, , 25°, , or1tan 20° tan 25°, , Solution:, , tan 2 0 +, , tan, , tan 25°, , (A, , +, , B) formula, , 1-tan 20° tan 25°, tan (20° + 25°) = tan 45°= l, Find the value of, , ., , an 155-tan 75°, 1+tan 135° tan 75, , Solution:, , tan135, , tan 75°, , 1+ tan135 tan 75°, , tan (A - B) formula, , tan (135- 75°) = tan 60° = 3, , PART BB, ., , Find the value of cos (60°- A) cos (30 + A)- sin (60°-A) sin (30° +A)., Solution:, , cos (60- A) cos (30 +A)-sin (60- A) sin (30 + A), , y 30 +AA, , cOs x cos y -sin x sin y, c o s (x +y) =, , cos 90° =, , x 60°-A, , 0, , x+y90], , 75

Page 6 :
74, , 2., , Engineering Mathematics-, , Find the value of sin 15., Solution:, sin 15°= sin (45° -30), sin 45° cos 30°- cos 45° sin 30°, , 22 22, 3., , 22, , Find hte value of cos 75., , Solution:, , cos (45°+30°), , cos 75°, , cos 45° cos 30°- sin 45° sin 30°, , .132/2 2/222, 4., , Prove that, , sin(A+ B)+ SinAD= tan A, , ., , cos(A+ B)+ cos(A - B), , Solution:, , LHSSinA cos B+ cos Asin B+ sin Acos B-cos, , A sin B, , cos A cos B-sin A sin B+ cos A cos B+ sin Asin B, , 2sin AcosB, 2 cos A cos B, , snA tan A= RHS, cos A, , 5. Prove that sin (A + B) sin (A - B) + sin (B+C) sin (B-C)+ sin (C+A) sin (C--A) =0., Solution:, , LHS, , sin (A + B) sin (A - B) + sin (B +C) sin (B-C)+ sin (C +A) sin (C-A), = sin?A - sin?B +sin B- sin'C + sin'C- sin?A = 0=RHS, , 6. If tan A -, , and tan B, , find the value of tan (A + B)., , 2, , Solution:, , tan(A+ B)=, , tan A+ tan B, 1- tan A tan B, , 2, , 3+, 2, , 5

Page 7 :
Trigonometry, 7., , Find the value of tan 105°, with out, , using tables., , Solution:, tan 105°, , tan, , (60° +45°), , tan60°+ tan 45°, , 1-tan 60°tan 45, V3+1 3+1, , 1-3x1 1-3, 8., , Prove that tan 20°, , 25°, , + tan, , + tan, , 20°, , tan, , 250 =1., , Solution:, 20°+25°=45°, tan (20°+25°) = tan 450, , tan 20°+tan 25°, , 1- tan 20° tan 25°, , =l|, , Cross multiplying, tan 200 +tan 250=1, , - tan 20° tan 25, , tan 20°+tan 25° +tan 20 tan 25° = 1, , PART-C, 1., , IfA and B are acute and, , if, , 1, , and sin B=, sin A= V10 an, , prove, , that A+B=, , Solution:, Given:, , sinA=, , and, sin B=, V10, , cosA= vi-sin? A cosB= v1-sin* B, , sinA=, , 5, , 9, , V10, 3, , sin B, , oCOSB, , coS A= -, , sin (A+ B) = sin A cos B+cos A sin B, , 2, vs0 50, 5, , 5, , 5, , S0 25x2 52, sin(A+B)=, , sin 45°, , 2, , A+ B= 45°= 180, , =

Page 8 :
76, , 2., , Engineering Mathematics-I, , IfA and B are acute and ifcos A =, , and cos B =,prove that A - B = 60°=, , 14, , Solution:, Given:, , cos A, , and, , 3, , B, , cos, , 14, , sinA= v- cos*A sin B= v1-cosB, , 196, , 49-1, , 196-169, , 49, , 196, 16x 3, , 49 49, , 9x3, V14x 14, , V196, , 45, , SinA v3, , 14, , 33, , COsA=, , 14, cos (A-B), , sinB=vV3, , CosB=3, , 14, , = cos A cos B + sin A sin B, , - x 4 3 , N3, 14, , 13,, 12x3, 98, 98, 13+ 36 491, =, , 98, , cos(A B)=, , 98 2, , cos60°, , 2, , A-B 60°= OU, 3, , 3., , IfA +B, , =, , 45°, prove that (1, , +, , tan A) (1, , + tan, , Solution:, , Given: A+B=45°, Taking tan on both sides, tan, , (A + B), , tan, , tan A+ tanB, , 1-tan Atan B, , 45, , 1, , tan A +tan B = I - tan A tan B, tan A + tan B + tan A tan B, , LHS= (1, , 1, , +tan A) (1+tan B), , I + tan B+ tan A + tan A tan B, =, , 2, , 1+1, , using (1), , RHS, , B), , =, , 2 and hence deduce the value, , of tan 22

Page 9 :
Trigonometry, , Put A 22,B- 22. Then A+ B 22+22, (1+, 22)1+ tan 22%-2, tan, , (say), , =2, , x= v2, 1+, , tan 22= v2, , tan22=2-1, , 45