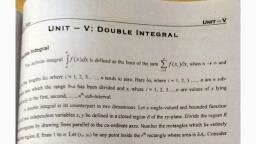Page 1 :
UNIT, Btep by Blay, - VI, UNIT, VI: TRIPLE INTEGRATION, 1. Triplo Integral, Consider a function r, y, 2) wlleh is continuoun at every point of a finite region v of three, dimensional space, Divide the region v into n mub-reglons of respective volumes Ov, where r1,2,3.., let (N, Vn z) be an arbitrary point in the sub-region. Consider the mum 2.S(x,,Y,,%,)ðv, , The limit, of this sum as n- o nnd Ov, - 0, ir it exists la called the triple integral of (x, y, z) over the region v and i, denoted by, SIS S(x, y, z)dv, where dv dx dy dz, For, of evaluntion, it, be cxpressed as, the, repeated integral, purpose, can, TII/(x, y, z) dx dy dz the order of integration depending upon the limits., Let, X1, X2 bc functions of y, z; yi, 2 are function of z and z,, zz bc constants., i.c., x = gi0, z), x2 = 8:0, z), yı - hi(z), y2 = h2(z) and z = a, z2 = b then the above integral is, evaluated as follows:, b h, (z) 82(y.=), SS S(x, y,z)dx dy dz = [ J J S(x,y,z)dx dy dz, a 4(z) K(y.z), SS S(x,y, z)dx dy dz = [{ | | S Scx, y,z)dx dy dz, 4(z)L(y.z), First f(x, y, z) is integrated with respect to x (kccping y and z constant) between the limits, XI = gı(, z), x2 = g20', z). The resulting cxpression, wliich is a function of y and z is then integrated with, respect to y (kceping constant) between the limits yI = h(z), y2 = h2(z)., %3D, %3D, The resulting expression, which is a function of z is then integrated with respect to z between the, limits z =a, z2 =b, If x1, X2, Yi, Y2, Zı, z2 are all constants, then the order of integration is immaterial, provided the, limits are changed accordingly. Thus,, [[[S(x,y,z)dx dy dz = [|[ S(x,y,z)dx dy dz, %3D, 278, Engineering Mathematics-, Scanned with CamScanner