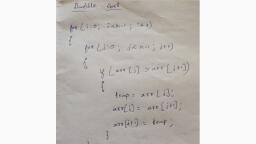Page 1 :
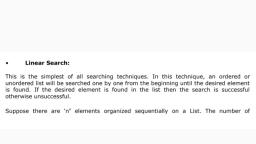
Merge Sort, To understand merge sort, we take an unsorted array as the following , [1 = [= J[ 19} JL JL), , We know that merge sort first divides the whole array iteratively into equal halves, unless the atomic values are achieved. We see here that an array of 8 items is divided, into two arrays of size 4., , (ws |=} [ss] lla), , This does not change the sequence of appearance of items in the original. Now we, divide these two arrays into halves., , (=l*) (=l=J (-f-), , We futher dvide these araye and we achieve atomic value which can no more be, , (+) &) FRAG ee&, , Now, we combine them in exactly the same manner as they were broken down. Please, note the color codes given to these lists., , We first compare the element for each list and then combine them into another list in a, sorted manner. We see that 14 and 33 are in sorted positions. We compare 27 and 10, and in the target list of 2 values we put 10 first, followed by 27. We change the order of, 19 and 35 whereas 42 and 44 are placed sequentially., , (l=) (#l=J (el), , In the next iteration of the combining phase, we compare lists of two data values, and, merge them into a list of found data values placing all in a sorted order., , (0 | le (=) (els ela), , After the final merging, the list should look like this ~, , | 10 || 14 | 19 || 27 | 3 35 |[ 42 | as |, , Now we should learn some programming aspects of merge sorting., Algorithm
Page 2 :
Merge sort keeps on dividing the list into equal halves until it can no more be divided., By definition, if it is only one element in the list, it is sorted. Then, merge sort combines, the smaller sorted lists keeping the new list sorted too., , Step 1 - if it is only one element in the list it is already sorted, return., Step 2 - divide the list recursively into two halves until it can no more be divided., Step 3 - merge the smaller lists into new list in sorted order., , Merge sort works with recursion and we shall see our implementation in the same way., , procedure mergesort( var a as array ), if(n == 1) returna, var |1 as array = a[0] ... a[n/2], var |2 as array = a[n/2+1] ... a[n], 11 = mergesort( 11 ), 12 = mergesort( |2 ), return merge( |1, 12), end procedure, procedure merge var a as array, var b as array ), var c as array, while ( a and b have elements ), if ( a[O] > [0] ), add b[0] to the end of c, remove b[0] from b, else, add a[0] to the end of c, remove a[0] from a, end if, end while, , while ( a has elements ), add a[0} to the end of c, remove a[0] froma, end while, , while ( b has elements ), add b[0] to the end of c, remove b[0] from b, end while, return c, end procedure