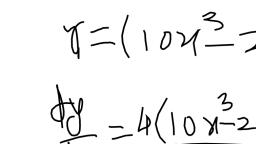Page 1 :
Maharashtra State Board Of Technical Education, Mumbai, Teaching And Examination Scheme For Post S.S.C. Diploma Courses, Program Name : Electronics Engineering Group, , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , | Program Code : DE/EJ/ET/EX/EN/EQ With Effect From Academic Year: 2017 - 18, Duration of Program : 6 Semesters Duration : 16 Weeks, Semester : Second Scheme - I, | ene Examination Scheme, Course | Theory Practical, Ss. . Course Credit ESE. PA Total ESE PA Total Grand, N. CourseeTitls Abbre | Code (L4T#P)) . 1] + Total, viation L|T| P xam, | Duration| Max | Min | Max | Min | Max | Min | Max | Min | Max | Min | Max) Min, | in Hrs. | Marks Marks) Marks|Marks) Marks | Marks) Marks Marks) Marks Marks | Marks) Marks, 1 | Applied Mathematics AME | 22210| 4 | 2] - | 6 | 3 | 70 2g | 30* | 00 | 100 | 40 -- - - | - - | = | 100, = T, | @ /iElements-ot Electrical EEC | 22215/ 4|-|2) 6 3 | 7 | 28 | 30*| 00 | 100 | 40 | 25# | 10 | 25 | 10 | so | 20 | 150, Engineering | |, 3. | Basic Electronics BEL | 22216| 4 | -| 4 8 3 | 70 28 | 30* | 00 | 100 | 40 | 50# | 20 | 50 20 | 100 | 40 | 200, > _——— t T i, Electronic Engineering EEM |22217/ 3 | -| - 3 3 10 28 | 30* | 00 | 100 | 40 _ a = we me oa 100, Materials, 5 | C Programming Language | CPR | 22218) 4 -|/ 4) 8 | 3 70 28 | 30* | 00 | 100 | 40 | SO@ | 20 50 20 | 100 | 40 | 200, : 7 ry T, Business Communication R@@mlsaqp0| - |-|2]/ 2 | - | -~ |~|-~|-—| — | — |ss@] 14] 15 | 06 | so | 20 | 50, | Using Computers | | |, Total 19 | 2/12) 33 = 350 = 150 | -- 500 | -- 160 | ~ 140 - 300 -__ 800, Student Contact Hours Per Week: 33 Hrs. . Medium of Instruction: English, Theory and practical periods of 60 minutes each. . Total Marks : 800, Abbreviations: ESE- End Semester Exam, PA- Progressive Assessment, L - Lectures, T - Tutorial, P - Practical, @ Internal Assessment, # External Assessment, *# On Line Examination, “ Computer Based Assessment, , , , * Under the theory PA, Out of 30 marks, 10 marks are for micro-project assessment (5 marks each for Physics and Chemistry) to facilitate integration of COs, and the remaining 20 marks is the average of 2 tests to be taken during the semester for the assessment of the cognitive domain LOs required for the attainment, of the COs., ~ For the courses having ONLY Practical Examination, the PA marks Practical Part - with 60% weightage and Micro-Project Part with 40% weightage, > If Candidate not securing minimum marks for passing in the “PA” part of practical of any course of any semester then the candidate shall be, declared as “Detained” for that semester., , , , MSBTE — Final Copy dt. 30.10.2017

Page 2 :
Applied Matinematies P Scheme, , , , ProgramName __: Electrical Engineering Program Group & Electronics, Engineering Program Group, Program Code: DE/EE/EJ/TE/IS/MU/ET/EN/EX, , Semester : Second, Course Title : Applied Mathematics, Course Code 222210, , 1. RATIONALE, , The core technological studies can be understood with the help of potential of applied, mathematics, This course is an extension of Basic Mathematics of first semester which is, designed for its applications in engineering and technology using the techniques of calculus,, differentiation, integration, differential equations and in particular complex numbers and, Laplace transform. Derivatives are useful to find slope of the curve, maxima and minima of, the function, radius of curvature, Integral calculus helps in finding the area. In analog to, digital converter and modulation system integration is important, Differential equation is used, in finding the curve and its related applications for various engineering models like LCR, circuits. This course further develops the skills and understanding of mathematical concepts, which underpin the investigative tools used in engineering., , 2. COMPETENCY, The aim of this course is to help the student to attain the following industry identified, competency through various teaching learning experiences:, © Solve electrical and electronics engineering related broad-based problems using, the principles of applied mathematics, , , , 3. COURSE OUTCOMES (COs), The theory, practical experiences and relevant soft skills associated with this course are to be, taught and implemented, so that the student demonstrates the following industry oriented, COs associated with the above mentioned competency:, , a, Calculate the equation of tangent. maxima,minima.radius of curvature by, , differentiation., , b. Solve the given problem(s) of integration using suitable methods., , c. Apply the concepts of integration to find the area and volume., , d, Solve the differential equation of first order and first degree using suitable methods., , e. Use Laplace transform to solve first order first degree differential equations,, , 4 TEACHING AND EXAMINATION SCHEME, , , , , , Examination Scheme, , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , Credit Theory Practical, ult |p [TP cer [ESE] PA Total ESE [PA | ‘Total, Hrs. (Max [atin | Max [Nin | Max | Min| Max | Mia | Max | Min | Max | Min, 4[2[~[ 6 3_| 70 [2a] 30° oo] too [ao] = | = | - | = | - | =, MSBTE — Final Copy dt. 30.10.2017 Page 1 of 7 1, , , , ‘Applic Mathematics # Seheme, , (*): Under the theory PA, Out of 30 marks, 10 marks are for micro-project assessment to, facilitate integration of COs and the remaining 20 marks is the average of 2 tests 10 be taken, ‘during the semester for the assessment of UOs required for the attainment of the COs., Legends: L-Lecture; T - Tutorial/Teacher Guided Theory Practice; P -Practical; C— Credit,, ESE -End Semester Examination; PA - Progressive Assessment, , COURSE MAP (with sample COs, Unit Outcomes i.e. UOs and topics), , ‘This course map illustrates an overview of the flow and linkages of the topics at various levels, of outcomes (details in subsequent sections) to be attained by the student by the end of the, course, in all domains of learning in terms of the industry/employer identified competency, depicted at the centre of this map., , , , , , , , , , , , , , , Gaui, , , , , , gmk, , \, , , , , , , , Figure 1 - Course Map, , 6. SUGGESTED PRACTICALS/ EXERCISES, The tutorials in this section are sub-components of the COs to be developed and assessed in, the student to lead to the attainment of the competency., , , , MSBTE - Final Copy dt. 30.10.2017 Page 2 of7 2

Page 3 :
pled Marheneiss 1 Setsine, init APPTOX., PA Tutorials wait, 7 Required, |_| Solve problems based on finding value of the fenction at different | I aT Tl, points,, |, | Solve problems to find derivatives of implicit function and T A, parametric function, 3 Solve problems to find derivative of logarithmic and exponential I 5, functions., 4 Solve problems based on finding equation of tangent and normal. I 2, 5 Solveproblems based on finding maxima, minima of function and | 1 %, radius of curvature at a given point., [6 | Solve the problems based on standard formulae of integration. I 2, 7 | Solve problems based on methods of integration, substitution, | II >, partial fractions, 8 | Solve problems based on integration by parts i | 2, 9 | Solve practice problems based on properties of definite integration. | Il | 2, jo Solve practice problems based on finding area under curve, areal Il |, between two curves and volume of revolutions. |, 11 | Solve the problems based on formation, order and degree of | IV 2 |, differential equations., [yy | Develop a model using variable separable method to related) IV ., | “* | engineering problem. |, | 13, | Develop a model using the concept of linear cifferential equation | 1V | z, to related engineering problem |, 14 | Solve problems based on algebra of complex numbers. vi[o2 i, 5 | FindLaplace transform and inverse Laplace transformusing related | V 2 |, properties,, 16 Make use of concept of Laplace transform to solve first order first) V 2 |, degree differential equation, a, , , , Note: The above tutorial sessions are Jor guideline only. The remaining tutorial hours are for, , revision and practice, , 7. MAJOR EQUIPMENT/ INSTRUMENTS REQUIRED, - Not applicable , 8. UNDERPINNING THEORY COMPONENTS,, , The following topics/subtopics is to be taught and assessed in order to develop UOs for, , achieving the COs to attain the identified competency:, , , , Unit Unit Outcomes (UOs), (in cognitive domain), , Topics and Sub-topics, , , , [Unit-1, , la. Solve the given simple problems | J.1 Functions and Limits :, Differential based on functions a: Concept of function and simple, Caleulus Ib, Solve the given simple examples, , problems based on rules of, differentiation 1.2 Derivatives :, le. Obtain the derivatives of 2, , b} Concept of limits without examples., , Rules of derivatives such as sum,, , , , MSBTE = Final Copy dt. 3¢.10.2017 Page 3 of 7, , Applied Mathematics, , U Scheme, , , , , , , , , , , , | Unit Unit Outcomes (UOs) Topics and Sub-topics, (in cognitive domain) _, logarithmic,exponential product, quotient of functions., functions. b) Derivative of composite functions, id. Apply the concept of (chain Rule), implicit and, differentiation to find equation parametric functions., of tangent and normal c) Derivatives of inverse, logarithmic, le. Apply the concept of and exponential functions, differentiation to calculate 1.3. Applications of derivative :, maxima and minima and a) Second order derivative without |, radius of curvature of givea examples |, problem, b) Equation of tangent and normal, c) Maxima and minima, d) Radius of curvature, Unit 2a. Solve the given problem(s) 2.1 Simple Integration: Rules of, Integral based on rules of integration. integration and integration of, Calculus 2b. Obtain the given simple standard functions,, integral(s) using substitution | 2.2. Methods of Integration:, method a) Integration by substitution,, 2c. Integrate given simple b) Integration by parts, functions using the integration | c) Integration by partial fractions, by parts., 2d. Evaluate the given simple, integral by partial fractions., Unit- I 3a. Solve given simple problems 3.1 Definite Integration:, Applications based on properties of definite a) Simple examples, of Definite integration. b) Properties of definite integral, Integration 3b. Apply the concept of definite (without proof) and simple, integration to find the area examples, under the given curve(s). 32 Applications of integration :, 3c. Utilize the concept of definite a) Area unde: the curve, integration to find area b) Area between two curves., between given two curves c) Volume of revolution, 3d. Invoke the concept of defirite, integration to find the volume, of revolution of given surféce, | Unit-1V 4a. Find the order and degree cf 4.1 Concept of differential equation, First Order given differential equations 42 Order. degree and formation of, First Degree 4b. Form simple difterential differential equation, Differential equations for given 43 Solution of differential equation, Equations engineering problem(s) a. Variable separable form, | 4c. Solve the given differential b. Linear differential equation, , , , , , , , dd., , ‘equations using the method of, variable separable., , Solve the given problems based, on linear differential equations, , , , 4.4 Application of differential equations, , , , , , and related engineering problems, , , , , , , , , , , , , , Page 4 of7

Page 4 :
Applied Mathomaties AU Scheme, , , , , , , , , , d. Laplace transform of derivatives, and solution of first order first, degree differential equations., , Note: To attain the COs and competency. above listed UOs need to be undertaken to achieve, , the ‘Application Level’ and above of Bloom's ‘Cognitive Domain Taxonomy, , Unit Unit Outcomes (UOs) Topics and Sub-topics, (in cognitive domain), [Unit-v ‘Sa. Solve given problems based on | 5.1 Complex numbers:, Complex algebra of complex numbers. | a. Cartesian, polar and exponential form, Numbers 5b. Solvethe given problems based | of a complex number., and on properties of Laplace b. Algebra of complex numbers, | Laplace transform 5.2 Laplace transform:, | transform. Se. Solve the given problems a. Laplace transform of standard, | based on properties of inverse | functions (without proof)., Laplace transform. |b. Properties of Laplace transform, Sd Invoke the concept of Laplace such as linearity, first and second, transform to solve first order | _ shifting properties (without proof)., first degree differential c. Inverse Laplace transform using, equations. partial fraction method, linearity and |, first shifting property,, , , , , , vi SUGGESTED SPECIFICATION TABLE FOR QUESTION PAPER DESIGN, , , , , , , , , , , , , , , , , , , , , , Unit Unit Title ‘Teaching | Distribution of Theory Marks, No. Hours R U A | Total, Level_| Level | Level | Marks, |_| Differential calculus [20 4 08 2 24, 1_| Integral calculus [14 02 06 08 16, Ti | Applications of Definite 0 | 02 2 04 08, Integration |, TV_| First Order First Degree 08 02 02 04 08, Differential Equations |, V_ | Complex numbers and 12 2 05 07 4, Laplace transform, I Total lL 64 12 23 35 70, , , , , , , , , , , , , , Legends: R=Remember, U=Understand, A=Apply and above (Bloom 's Revised taxonomy), Note: This specification table provides general guidelines to assist student for their learning, and 10 teachers to teach and assess students with respect to attainment of UOs. The actual, distribution of marks at different taxonomy levels (of R, U and A) in the question paper may, vary from above table., , 10. | SUGGESTED STUDENT ACTIVITIES, Other than the classroom learning, following are the suggested student-related co-curricular, activities which can be undertaken to accelerate the attainment of the various outcomes in this, course, , a Identify engineering problems based on real world problems and solve with the use of, , free tutorials available on the internet., b. Use graphical software's: EXCEL, DPLOT, and GRAPH for related topics., c. Use Mathead as Mathematical Tools and solve the problems of Calculus., , , , MSBTE — Final Copy dt 30.10.2017 Page 5 of7, , , , , Applied Mathematics {F Schone, , d. Identify problems based on applications of differential equations and solve these, , problems., , Prepare models to explain different concepts of applied mathematics., , Prepare a seminar on any relevant topic based on applications of integration, , g. Prepare a seminar on any relevant topic based on applications of Laplace transform to, related engineering problems, , mo, , 11. SUGGESTED SPECIAL INSTRUCTIONAL STRATEGIES (if any), These are sample strategies, which the teacher can use to accelerate the attainment of the, various outcomes in this course:, a. Massive open online courses (MOOCs) may be used to teach various topics/sub, topics., b. ‘L’ in item No. 4 does not mean only the traditional lecture method, but different, types of teaching methods and media that are to be employed to develop the outcomes, c. About 15-20% of the topics/sub-topics which is relatively simpler or descriptive in, nature is to be given to the students for self-directed learning and assess the, development of the COs through classroom presentations (see implementation, guideline for details)., , d, With respect to item No.10, teachers need to ensure to create opportunities and, provisions for co-curricular activities, , eGuide student(s) in undertaking micro-projects, , f Apply the mathematical concepts learnt in this course to branch specific problems, , g. Use different instructional strategies in classroom teaching, , h. Use video programs available on the internet to teach abstract topics, , 12. SUGGESTED MICRO-PROJECTS, , Only one micro-project is planned to be undertaken by a student assigned to him/her in the, beginning of the semester. S/he ought to submit it by the end of the semester to develop the, industry oriented COs. Each micro-project should encompass two or more COs which are in, fact, an integration of UOs and ADOs. The micro-project could be industry application based,, internet-based, workshop-based, laboratory-based or field-based, Each student will have to, maintain dated work diary consisting of individual contribution in the project work and give a, seminar presentation of it before submission. The total duration of the micro-project should, not be less than 16 (sixteen) student engagement hours during the course., , In the first four semesters, the micro-project could be group-based. However, in higher, , semesters, it should be individually undertaken to build up the skill and confidence in every, , student to become problem solver so that s/he contributes to the projects of the industry. A, , suggestive list is given here. Similar micro-projects could be added by the concemed faculty:, a, Prepare models using the concept of tangent and normal to bending of roads in case of, , sliding of a vehicle., , b. Prepare models using the concept of radius of curvature to bending of railway track, , c. Prepare charts displaying the area of irregular shapes using the concept of integration, , d. Prepare charts displaying volume of irregular shapes using concept of integration, , e. Prepare models using the concept of differential equations for mixing problem., , f Prepare models using the concept of differential equations for radio carbon decay, , g. Prepare models using the concept of differential equations for population growth., , h. Prepare models using the concept of differential equations for thermal cooling,, , i, Prepare models using the concept of Laplace transform to solve linear differential, , equations., , , , MSBTE — Final Copy dt. 30.10.2017 Page 6 of 7 2