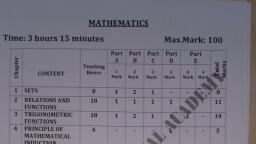
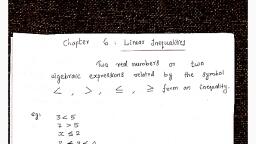Page 1 : LINEAR INEQUALITY, , TOPIC-1-ALGEBRAIC SOLUTIONS OF LINEAR, INEQUALITIES IN ONE VARIABLE, , f ( x) and g ( x) are polynomials in x are called rational, algebraic inequalities., , LINEAR INEQUALITIES, , 1. If two numbers or algebraic expressions are related, by the symbols ' ' , ' ' , ' ' or ' ' then they are, said to form an inequality., 2. An expression of the form, , ax b c , ax b c , ax b c , ax b c ,, where a, b, c are real numbers, with x 0 , is called, , linear inequality in one variable x., 3. A solution set of an inequality is the set of all real, numbers that satisfy the inequality. The method of, finding the solution set of an inequality is known as, solving the inequality., 4. During the process of solving an inequality, following rules are followed, The inequality does not change, if we add or, subtract the same number on both The sides of the, inequality i.e. a b a k b k k R, The inequality does not change; if we multiply or, divide both the sides by the same positive real, number i.e., a b, k is a real, a b ka kb and a b , k k, number., The inequality reverses in its direction if we, multiple both the sides of the inequality by the, same negative real number i.e., a b ka kb if k 0 and a b , , 1 1, , a b, , Note: The similar results hold good in the case of other, inequality signs ' ' , ' ' or ' ' , 5. Two or more linear inequalities are one variable are, together said to form a system of linear inequalities, more variable., Examples: 3x 7 5 x,, , 11 5 x 1, , 6. Absolute value of a real number x, is denoted by, , x if x 0, and defined by x , , x if x 0, 7. Rational algebraic inequalities, The inequalities of the form, f ( x), f ( x), f ( x), f ( x), 0,, 0,, 0,, 0 where, g ( x), g ( x), g ( x), g ( x), , x, , SHORT CUT METHODS, 1., , x 0 if x R, , 2., , x a a x a, i.e. x a , a , , 3., , x a a x a, i.e. x a , a, , 4., , x a x a or x a i.e. x , a a , , , 5., , x a x a or x a i.e. x , a a , , , 6., , x a b a b x a b i.e. x a b, a b, , 7. x a b x a b or x a b i.e. x , a b a b, , 8. The solution set of a b , , xa, 0 is x , a b, , xb, , The solution set of, xa, 0 is x , a b, , xb, xa, 0 is x a , b , 10. The solution set of, xb, 9., , 11. The solution set of, , 12. The solution set of, xa, 0 is x , c b, a where a b c, x bx c , 13. Triangular inequality, , x y x y x, y R, x y x y x, y R, 14., , xy x y, , 15., , x, x, , y, y, , 16., , x x x R, , 17. If a1 a 2 , a 2 a3 ........ a n 1 a n , then a1 a n, 18. If a b 0 then, a2 b2, , , , a b, , , , 1 1, , a b, , 19. If, CHETHAN M G, , xa, 0 is x a , b , xb, , a 0 b then, ,
[email protected], Phon number-8105418762 / 7019881906, , 1
Page 2 : CONCEPTS OF MATHEMATICS FOR KCET JEE MAIN & ADVANCED, , , , a b if a b, , , , a 2 b 2 if a b, , 2, , 2, , 20. If a x b and a, b are positive real numbers,, then a 2 x 2 b 2, 21. If a x b and a is a negative number and b is, a positive numbers, then, , , , 0 x 2 b 2 if b a, , , , 0 x b if a b, , 22. If, , 2, , 2, , a, 0 then, b, , a 0 if b 0, a 0 if b 0, 23. If ai bi 0 where i 1,2,3...... n then, a1 a 2 a3 ...a n b1b2 b3 ...bn, 24. If ai bi where i 1, 2,3...n then, a1 a 2 a3 ... a n b1 b2 b3 ... bn, 25., , If x x 0 , then x , , If x x 0 , then x , , If x x 0, then x , , , If x x 0, then x , , 26. If a b c are the sides of a triangle, then, , 12. If, , a) x –2, b) x – 2, c) x < – 2, d) x > –2, Solution:(d), 2. Given that x, y and b are real numbers and, x y, b 0, then, a) x y, b) x y, b b, b b, x y, c) , d) x y, b b, b b, Solution:(c), 3. If 3x 17 13 then, a) x 10, , b) x 10, , c) x ,10 , d) x 10,10 , Solution:(a) 3x 17 13, 3x 13 17 3x 30 x 10, x 10, , , , , 4. If x is a real numbers and x 3 then, a) x 3, b) 3 x 3, c) x 3, d) 3 x 3, Solution:(b) x 3 3 x 3, 5. x and b are real numbers. If b 0 and x b, then, , a, b, c, , , 1 a 1 b 1 c, SOLVED PROBLEMS, LEVEL-I, , 1. If x 5 then, a) x 5, b) x 5, c) x 5, d) x 5, Solution:(c) x 5 x 5, 9. If x > y and z < 0 then, a) –xz < – yz, b) –xz – yz, c) –xz > –yz, d) –xz –yz, Solution:(c), 10. If x < –5 and x > 2 then, a) x (–5, 2), b) x (–5, ), c) x (–, 2), d) no solution, Solution:(d), 11. If p > 0 and q < 0 then, a) p + q < p, b) p + q > p, c) p + q p, d) p + q p, Solution:(a), 2, , 2, 0 then, x2, , a) x b, , , b) x , b , , c) x b, b , , d) x , b b, , , Solution:(d) x b, x , b b, , 6. If x 1 5, then, a) x 4, 6 , b) x 4, 6, c) x , 4 6, , d) x , 4 6, , Solution:(c), , x 1 5,, , x 1 5 Or x 1 5, x 6 Or x 4 x , 4 6, , , 7. If x 2 9, then, a) x 7,11, , b) x 11,7 , , c) x , 7 11, , , d) x , 7 11, , , Solution:(b) x 2 9,, , 9 x 2 9 11 x 7 x 11, 7, ,
[email protected], Phon number-8105418762 / 7019881906, , MCP-MATHEMATICS
Page 3 : LINEAR INEQUALITY, , 8. If x 2 9, then, b) x 11,7 , , a) x 7,11, c) x , 11 7, , , d) x , 7 11, , , Solution:(c) x 2 9,, , x 2 9 x 11 Or x 2 9 x 7, x , 11 7, , , 9. If x 5 10, then, a) x 15,5, , b) x 5,5, , c) x , 15 5, , , d) x , 15 5, , , [KCET-2018-1M] [One option correct type], , Solution:(c) x 5 10,, , x 5 10 x 15 Or x 5 10 x 5, , x , 15 5, , , 10. The set of all real number x for which, x 2 x 2 x 0 is, b) , 2 2, , d), 2, , , a) , 2 2, , , , , c) , 1 1, , , , , Solution:(b) x x 2 x 0, 2, , (i) If x 2 1, , x2 x 2 x 0, x2 x 2 x 0, , x2 2 0 x2 2, , , , , , x , 2 , , x 2, , , , 2, 2 , , (ii) If x 2 3, , x2 x 2 x 0, x2 2x 2 0, d 2 4ac 22 4 1 2 4 0, So solution does not exists, , , , , , x , 2 , , , , 2, 2 , , 11. Solution of a linear inequality in variable x is, represented on number line in, a) x ,5, c) x 5, , , 5, , Solution:(d) x 5, , , CHETHAN M G, , b) x ,5, , d) x 5, , , 9. The length of a rectangle is three times the breadth., If the minimum perimeter of the rectangle is 160, cm, then, a) breadth > 20 cm, b) length < 20 cm, c) breadth 20 cm, d) length 20 cm, Solution:(c) If x cm is the breadth then, 2(3x + x) 160 x 20, breadth 20 cm, 10. The longest side of a triangle is twice the shortest, side and the third side is 2 cm longer than the, shortest side. If the perimeter of the triangle is, more than 166cm then the minimum length of, shortest side is, a) 82 cm, b) 41 cm, c) 42 cm, d) 81 cm, Solution:(b)Let shortest side be x cm. Then longest, side = 2x cm. Third side x + 2, By data x + 2x + (x + 2) > 166, 4x > 164 or x > 41 cm, 11. In drilling world’s deepest hole, it was found that, the temperature T in degree celcius, x km below the, earth’s surface was given by T = 30 + 25(x – 3),, 3 x 15. T then range of x where temperature is, between 155C and 205C is, a) 8 < x < 10, b) 8 < x < 9, c) 18 < x < 20, d) 9 < x < 10, Solution:(a) 155 < 30 + 25x – 75 < 205 8 < x < 10, 12. A company manufactures cassettes. Its cost and, revenue functions are C(x) = 26000 + 30x and R, (x) = 43x, respectively, where x is the number of, cassettes produced and sold in a week. The, minimum number of cassettes must be sold by the, company to realize some profit is, a)1000 b) 1500 c) 2600 d) 2000, Solution:(d) profit = R(x) – C(x), To achieve some profit, R(x) – C(x) > 0, 43x > 26000 + 30x 13x > 26000 x > 2000, 13. If 1 |x – 2| 3 then, a) x (–, 1) [3, ), b) x [–1, 5], c) x [–1, 1] [3, 5], d) x (–, 5], Solution:(c) |x – 2| 1 and |x – 2| 3, (x – 2 –1 or x – 2 1) and (–3 x – 2 3), (x 1 or x 3) and (–1 x 5), x (–, 1] [3, ) and x [–1, 5], Combining the solutions of two inequalities we, have x [–1, 1] [3, 5], ,
[email protected], Phon number-8105418762 / 7019881906, , 3
Page 4 : CONCEPTS OF MATHEMATICS FOR KCET JEE MAIN & ADVANCED, , 3x 4 x 1, 12. The solution set of the in equation, , 1, 2, 4, is, a) 0,1, b) 1, , d) 1, , , c) 1, , , 3x 4 x 3, 3x 4 x 1, , 1 , , 2, 4, 2, 4, 2 3 x 4 x 3 6 x 8 x 3 , , Solution:(b), , w.n.t x a x a or x a i.e. x , a a , , 5x 6 8 Or, 5x 6 8, Or, 5x 14, 5x 2, 14, 2, 2 14 , , Or, x, x, x , , , 5, 5, 5 5 , , 17. The solution set of the in equation 4 x 3 27 is, , a) 6, 15 , , x5, 0 is, x2, b) 5 x 2, d) 5 x 2, , 13. The solution set of the in equation, a) 5 x 2, c) 5 x 2, , Solution:(d) w.k.t x a a x a, i.e. x a , a , 4 x 3 27, 27 4 x 3 27, , x 5 , Solution:(a) x 5 0 , 0, x2, x2, xa, w.n.t, 0 is x a , b , xb, , 24 4 x 30, 6 x , , a) , 5 2, , , x5, 0 is, x2, b) 5 x 2, , c) 5 x 2, , d) 5 x 2, , 14. The solution set of the in equation, , Solution:(a) x 5 0 , x2, w.n.t, , x2, , x , 5 2, , 15. The solution set of the in equation x 3 0 is, x4, , b) , 4 3, , d) , 4 3, , , xa, Solution:(c) w.n.t, 0 is x , a b, , xb, x3, x 3, 0, 0, x4, x 4 , 16. The solution set of the in equation 5 x 6 8 is, , , 5 , , 5, , , , c) , 2 14 , , 5 5 , , Solution:(a) 5x 6 8, 4, , 15 , 15, , x 6, , 2, 2, , , b) , 2 14 , , 5 5 , , 2 14 , d) ,, ,, 5 5 , , , a) x 1,3, , b) x 1,3 , , c) x 1,3, , d) x 1,3, , 1 x 2 1, 1 2 x 2 2 1 2, 1 x 3, x 1,3, 19. The solution set of the in equation 6 x x 2 0 is, a) 1 x 2, b) 2 x 3, c) 2 x 1, d) None of these, 2, Solution:(b) 6 x x 0 x 2 x 6 0, , x 2 x 3 0, , x 2 x 3 0, x 2,3, , , , , , 20. If x 2 5x 4 x 2 5x 4 then x belongs to, a) 2, , c) 2, , Solution:(b), , x , 4 3, , a) , 2 14 , , , , Divide by 4, , Solution:(a) x 2 1, , 0, , xa, 0 is x , a b, a b , xb, , a) , 4 3, , c) , 4 3, , , add 3, , 18. If x 2 1 ,then, , 5 x 2, , x 5 , , , 2 , d) 6, 15 , 2, , , 2 , , c) 6, 15 , 2 , , , 6x x 8 3 5 x 5 x 1, x 1, , , b) 6, 15 , , b) , , d) 2, , , 21. The solution set of the in equation, a) 2, , , c) 2, , Solution:(a), , b) 2, , , x2, 0 is, x2, , d) 2, , , Clearly x 2 & x 2 0, , x 2 0 x 2 x 2, , ,
[email protected], Phon number-8105418762 / 7019881906, , MCP-MATHEMATICS
Page 5 : 22. The minimum value of f x 3 x 7 is, a) 0, b) 6, c) 7, d) 8, Solution:(c) f x 3 x 7 7 x R, x2, 23. Solution set of inequality loge , is, x3, a) 2, , b) , 2, c) , , d) , 2 3, , x 2 is defined as, f x log e , , x3 , , Solution:(d), , x2, o, x 3 , x ,2 3, , when , , 24. If, , r is a real number such that, , r 1 and if, , a 5 1 r then, a) 0 a 5, b) 5 a 5, c) 0 a 10, d) 0 a 10, Solution:(a) r 1 1 r 1, Put r 1 a 5 1 2 10, Put r 1 a 5 1 1 0, 0 a 10, 25. The set of all solution of the in equation, x 2 2 x 5 0 in R is, a) R , 5, b) R 5, , , d) R , 4, , c) , , Solution:(c) x 2 x 5 0, 2, , 2, , x R x 1 4 0, 2, , LEVEL-II, , The set A x : 2 x 3 7 is equal to the, set, a) B x : 3 x 7, b) C x : 13 2 x 4, c) D x : 0 x 5 7, d) E x : 7 x 7, , [KCET-14-1m] [Only one option correct], , Solution:(c) A x : 2 x 3 7, , A x : 7 2 x 3 7, A x : 10 2 x 4, A x : 5 x 2, A x : 0 x 5 7 D, CHETHAN M G, , b) 1, 9 ,6, d) , 6 1 , , , a) 1, 9, c) 1, 9 , , Solution:(d) (i)w.n.t x a a x a, i.e. x a , a , , 5 x 4 5 1 x 9 x 1,9 1, (ii) w.n.t x a x a or x a i.e. x , a a , , Or, 2x 5 7, 2x 5 7, Or, 2x 2, 2x 12, Or, x 1, x 6, x , 6 1, 2 , From 1 & 2 x , 6 1, 1,9 , , x 1,9 , 27. The solution set of the in equation x 2 8 8 is, b) , 4, d) 4, , , a) , , c) 4, 4, , Solution:(a) w.n.t x a a x a, i.e. x a , a, 8 x 2 8 8 0 x 2 16, (i) 0 x2 x R 1, , (ii) x 2 16 4 x 4 x 4, 4 2 , From 1 & 2 x R 4, 4, , x 4, 4, 28. The solution set of the in equation, b) 3, 0, d) 1,1, , a) 3,1, c) 3, 1, , x 1 4 0, , 1., , LINEAR INEQUALITY, , 26. The solution set of the in equation x 4 5 ,, 2 x 5 7 is, , x2 2x 3, 0 is, x2 1, , x2 2x 3, 2, 0 Clearly x R, x 1 0, x2 1, x2 2x 3 0, x 3 x 1 0, , Solution:(a), , x 3 x 1 0, , w.n.t x x 0 , then x , , , x 3,1, 29. The solution set of the in-equation, a) 7,1, c) 7, 4 4,1, , x2 6x 7, 0 is, x4, , b) 7, 4, d) 7, 4 4,1, , [KCET-15-1m] [Only one option correct], , Solution:(c), , x2 6x 7, 0, x4, ,
[email protected], Phon number-8105418762 / 7019881906, , 5
Page 6 : CONCEPTS OF MATHEMATICS FOR KCET JEE MAIN & ADVANCED, , Clearly x R, x 4 0 but x 4, , x 2 4 x 5 0 x 5 x 1 0, , x 5 x 1 0 x 1,5, , x 2 6 x 7 0 x 7 x 1 0, , x 7 x 1 0 x 7,1, , From 1 & 2 x R 1,5 x 1,5, , x 7, 4 4,1, , 33. If 3 x 1 7 then which of the following does, 4, 2 2, not belong to its Solution set?, 25, 111, a) 0, b) 119, c), d), 32, 4, 25, 3, x, 1, 7, Solution:(d), , 4, 2 2, 7 3x 1 7, , , 2 4 2 2, 7 1 3x 1 1 7 1, , , 2 2 4 2 2 2 2, 3x, 16, 3 , 4, 4 x , 4, 3, 25, Does not belong to the Solution set, 4, 34. The solution set of the in equations, 2, 1, x 4 is, x4, a) 2, 6, b) 1, 4 4, 6, c) 2, 4 4, 6, d) 2, 4 6, 8, Solution:(c) Clearly x 4, , 30. x denotes the greatest integer less than or equal, x 6 0 is, to x, then the Solution of, 8 x, b) 7, 8, , a) 6, 7, , c) 7, 8, d) 6, 7, Solution:(b), x 6 0 x 6 0, 8 x, x 8, , xa, 0 is x a , b , xb, 6 x 8 x 7 x 7, 8, , w.n.t o, , 31. The solution set of the in equation x 2 x x 1 0, is, a) , , b) , 4, c) 4, 4, d) , Solution:(d), (i) If x 0 x 2 x x 1 0 x 2 2 x 1 0, , x 1 0 This is not possible case, 2, , (ii) If x 0 x x x 1 0 x 1 0, This is not possible case, Solution set is , 32. The solution set of the in equations, x4 x2 1, x2 6x 7, and, , 2, , 0, 0 is, x2 1, x2 4x 5, a) 1, 5, b) 5,1, c) , , d) 2, 3, 2, , x2 6x 7, Solution:(a) (i), 20, x2 1, x2 6x 9, x2 6x 9, , , 0, , 0, x2 1, x2 1, , x 3, , , 2, , x2 1, , 0, , x , 1, , x4 x2 1, 0, x2 4x 5, Clearly x R, x 4 x 2 1 0, (i), , 6, , 2, 1 x4 2, x4, , 2, , 2 x 4 2 2 x 6, x 2, 4 4,6 , , 35. If x 2 4ax 2 0 for all values of x ,then a lies in, the interval, a) 2, 4, b) 1, 2, c) 2 , 2 , , d) 1 , 1 , 2, , 2, , Solution:(d) w.n.t ax bx c 0 iff a 0 & D 0, 2, , x 2 4ax 2 0, D 0 4a 4 1 2 0, 2, , 1, 2, , 1, 1, a, 2, 2, 2, 36. If x 2 x n 10 , x R then which of the, following conditions is true?, a) n 11 b) n 10 c) n 11 d) n 11, Solution:(d) w.n.t ax 2 bx c 0 iff a 0 & D 0, 16a 2 8 0, ,
[email protected], Phon number-8105418762 / 7019881906, , a2 , , , , x 2 2 x n 10 0, MCP-MATHEMATICS
Page 7 : a) , 2 2, , , D 0 2 4 1 n 10 0, 2, , c) , 1 1, , Solution:(a), , 4 4n 40 0 4n 44 0 4n 44, n 11, 37. For all x 2 2ax 10 3a 0 ,then the, interval in which a lies is, a) a 5, b) 5 a 2, c) a 5, d) 2 a 5, 2, Solution:(b) w.n.t ax bx c 0 iff a 0 & D 0, , a) 120, , , 5 a 2, 38. The solution set contained in R of the in equation, 3x 31 x 4 0 is, a) 1, 3, b) 0, 1, c) 1, 2, d) 0, 2, Solution:(c) 3x 31 x 4 0, 32 x 3 43x 0 32 x 43x 3 0, 32 x 33x 3x 3 0 3x 3x 3 1 3x 3 0, , , , , , 1 3x 3 10 3x 31, , 0 x 1, 39. The solution set of the in equation, 8sec 2 6 sec 1 0 is, a) , b) R 2n 1 : n Z , 2, , , c) R n : n Z , d) R, 2, , Solution:(a) 8sec2 6 sec 1 0, 8sec2 4sec 2sec 1 0, , 4sec 2sec 1 1 2sec 1 0, , 2sec 1 4sec 1 0, 1 , 1, , 2 sec 4 sec 0, 2 , 4, , 1 , 1, , sec sec 0, 2 , 4, , 1 1, sec , Which is impossible, 4 2, 40. The set of all real number x for which, x 2 x 2 x 0 is, CHETHAN M G, , d) 120,0, , Solution:(b) we have 1 3 x 4 1 x 6 , 25, 3, , a 5 a 2 0, , , , 3, , b) ,120, , c) 0,120, , 4a 2 40 12a 0, a 2 3a 10 0, a 5 a 2 0, , , , , , is, , 2, , 3x 3 3x 1 0, , , , 25, , D 0 2a 4 110 3a 0, , , , , , 41. The solution set of in equation 1 3 x 4 1 x 6 , , x 2 2ax 10 3a 0, , , , LINEAR INEQUALITY, , b) , 2 2, , d) 2 , , , 1 3 x 20 1, , x 6, 2 5 3, 3x 20 x 6, , , 10, 3, 3 3x 20 10 x 6 , , 9x 60 10x 60, 9x 60 60 60, x 120, x 120, x ,120, , Hence, the solution set of the given in equation is, , ,120, , 42. If 5 x 3 x 39 and 2 x 1 x 1 3x 1 ,then, 4, 8, 8, 12, 3, 4, 5 x 3 x 39, belongs to the interval, , , 4, 8, 8, , a) 3, , , b) 0, , , c) ,3, , d) , 0 , , Solution:(a) 5 x 3 x 39 and 2 x 1 x 1 3x 1, 4, 8, 8, 12, 3, 10 x 3 x 39, 2 x 1 4 x 4 3x 1, and, , , , 8, 8, 12, 4, 13 x 39, and 2 x 3 3 x 1, , , 4, 8, 12, 4, 13x 39 and 2x 3 9x 3, x 3 and x 0, x 3, and x 0, x 3, , , 4, , 43. The set of all values of, x satisfying the in, equations x 1 5 and x 2 is, a) 4, 6, , b) 4, 2, , c) 4, 2 2,6, , d) 2, 6, , Solution:(c) x 1 5 and x 2, 5 x 1 5 and x 2 or x 2 ,
[email protected], Phon number-8105418762 / 7019881906, , 7
Page 8 : CONCEPTS OF MATHEMATICS FOR KCET JEE MAIN & ADVANCED, , 4 x 6 and x 2 or x 2 , x 4,6 and x , 2 2, , x 4, 2 2, 6, , 44. If the solution set of the in equation 3 1 is, x 2, a) 1,1, , b) 1,1, , Solution:(a), , 3, 1, x 2, , c) ,1, , a) R 0, , b) R 1,0,1, , c) R 1, , d) R 1,1, , Solution:(b) x , , x2 1, 2, x, , d) 1, , , x2 1, 2 x 2 1 0, x, , 3 x 2, , x2 1 2 x, , 1 x x 1 x 1,1, x, , a) 1, 2 , , b) 0,1, , c) 1, 0 , , d) 1, , , x 2 x 1 0, 2, , 45. If x 1 2 then x belongs to the interval, , x 1, , 2, , 46. The set of all values of x satisfying the in, equations x 1 x 1 0 is, b) , 1, , c) 1, 1, , d) , 1, , Solution:(c) 5x 1 x 1 7 x 3, 2, , 5x 1 x 1 and x 1 7 x 3, 2, , 2, , 2, , 0, , for all x R , , , equations 5x 2 3x 8 and , x 2 4 is, , 0 , then x lies to the interval, , b) 2, 2 , , Solution:(c)we have, , d) 1, 1, x 1, x 2, , 0, , 1 x 2, , x 2, 1 1, 2 , 48. Solution of x , , 2, , 50. The set of values of x satisfying the system of in, , 1 x 1 x 1,1, , c) 2, 1 1, 2, , 2, , x 2, 4 , , x 1 x 1 ( x 1) 0, , a) 1, 2 , , d) ,1 2, , , x ,1 2, and x 1, 4 , , 3, , x 2, , c) 2, 4 , , x 2 3x 2 0 and x 2 5 x 4 0, x 1 x 2 0 and x 1 x 4 0, , Solution:(a) x 1 x 1 0, , 47. If, , b) 2, 4, , 2, , a) 1,1, , x 1, , a) 1, 4 , , x 1 5x 1 0 and x 1 7 x 3 0, , 3, , x 1, , 0 x 1 x 1, 1, , 49. The solution set of 5x 1 x 1 7 x 3 is, , x 1, x 1, x 1, x 1, 2, 20, 0, 0, x, x, x0, x0, x 1, , 0 x 1, 0 , x0, , , , , 2, , x R 1,0,1, , Solution:(c)we have, , x 1 ( x 1) 0, , 1, 2 Clearly x 0, x, , x 1, , a) ,1, , b) 2,3, , c) ,3, , d) ,1 2,3, , Solution:(d) 5x 2 3x 8 and x 2 4, x 1, x, , 2, 2x 6 0 and, 40, x 1, 3 x 6, 2 x 3 0 and, 0, x 1, x2, x 3 0 and, 0, x 1, x ,3 and x ,1 2, , , 1, 2 is, x, , x ,1 2,3, , 51. The set of real values of x satisfying the, 8, ,
[email protected], Phon number-8105418762 / 7019881906, , MCP-MATHEMATICS
Page 9 : LINEAR INEQUALITY, , inequality x2 x 6 6 , is, a) 4,3, , b) 3, 2 , , c) 4,3 2,3, , d) 4, 1 0,3, , Solution(d)we have x2 x 6 6, 6 x 2 x 6 6, 6 x 2 x 6 and x 2 x 6 6, x 2 x 0 and x 2 x 12 0, , x x 1 0 and x 4 x 3 0, x , 1 0, and 4 x 3, x 4, 1 0,3, LEVEL-III, , CHETHAN M G, ,
[email protected], Phon number-8105418762 / 7019881906, , 9