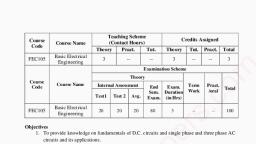
Page 1 :
AC CIRCUITS, Module 2, , 08:56
Page 2 :
An sinusoidally varying alternating, (AC) quantity, • An alternating (AC) quantity continuously, changes in magnitude and alternates in, direction at regular intervals of time., , 08:56
Page 3 :
An sinusoidally varying alternating, (AC) quantity, , Instantaneous value of alternating voltage, , e = Em sinwt, 08:56
Page 4 :
The important terms associated with, an alternating quantity are given, below, , • 1. Amplitude: It is the maximum or peak value, attained by the alternating quantity., • 2. Time period (T): It is the time taken in, seconds for completing one cycle of an, alternating quantity., • 3. Cycle: an alternating quantity either voltage, or current when completes one set of positive, and negative values. One cycle is equal to 2π, radian or 3600 electrical degree., 08:56
Page 5 :
The important terms associated with, an alternating quantity are given, below, , • 4. Instantaneous value: It is the value of the, alternating quantity at a particular instant in, time., • 5. Frequency: This represents the number of, cycles that occur in a second. The unit of, frequency is Hertz (Hz) or cycles / sec,, mathematically f = (1/T) or also T = (1/f)., , 08:56
Page 6 :
The important terms associated with, an alternating quantity are given, below, , 08:56
Page 7 :
Magnitude of Alternating Voltage and, Current, • There are three ways to measure magnitude, of alternating voltage and current., • 1. Peak value., • 2. Average or mean value., • 3. R.M.S value., , 08:56
Page 8 :
Peak value, • The maximum value attained by an alternating, quantity either voltage or current during one, cycle is called the peak value. It is also known, as amplitude and denoted as Emax or Imax., , 08:56
Page 9 :
Average value, • The arithmetic mean of all the instantaneous, values of an alternating quantity over one, cycle is known as average value., , 08:56
Page 10 :
Average value, • Since in symmetrical waves like sinusoidal current or, voltage wave +ve half is equal to -ve half, the average, value over a complete cycle is zero. Therefore, for, alternating quantity average value is considered only, for +ve half of the cycle., , 08:56
Page 11 :
Average Value of Sinusoidal Current, • Consider an elementary area of width dθ in, the +ve half of an alternating current. If i is the, mid ordinate of the strip, then area of strip:, , Equating an alternating current, , I = Imax sinwt, 08:56
Page 12 :
Average Value of Sinusoidal Current, , 08:56
Page 13 :
R.M.S Value (Root mean Square, value), , 08:56
Page 14 :
R.M.S Value of Sinusoidal Current, • The equation for sinusoidal alternating current, is given by:, I = Imax sinwt, , 08:56
Page 15 :
R.M.S Value of Sinusoidal Current, , 08:56
Page 16 :
R.M.S Value of Sinusoidal Current, , 08:56
Page 17 :
R.M.S Value of Sinusoidal Current, • Base of half cycle = π, , 08:56
Page 18 :
Form Factor, • The ratio of r.m.s value to average value of an, alternating quantity is known as form factor:, , 08:56
Page 19 :
Peak Factor, • Peak factor is the ratio of maximum value, to r.m.s value of an alternating quantity is known as, peak factor., , 08:56
Page 20 :
An alternating current ‘i’ is given as i = 141.4 sin 314t, find a), maximum value b) frequency c) time period d) instantaneous, value when t = 3 ms., , • a) It is in the form i = , so Im= 141.4 A., , • b) We know, ω = 2Πf, here, ω = 314,, therefore, f = 314/2x3.14 = 50 Hz., , 08:56
Page 21 :
An alternating current ‘i’ is given as i = 141.4 sin 314t, find a), maximum value b) frequency c) time period d) instantaneous, value when t = 3 ms., , • a) It is in the form i = , so Im= 141.4 A., , • b) We know, ω = 2Πf, here, ω = 314,, therefore, f = 314/2x3.14 = 50 Hz., , 08:56
Page 22 :
An alternating current ‘i’ is given as i = 141.4 sin 314t, find a), maximum value b) frequency c) time period d) instantaneous, value when t = 3 ms., , • c) Time period t = 1/f = (1/50) = 0.02 sec., • d) Instantaneous value, • ‘i’ = 141.4 sin (314 x 3 x 10-3 x 180/3.14 ) =, =141.4 sin (540), = 114.35 A, , 08:56
Page 23 :
What is Phase, • The phase is defined as the position of the, waveform at a fraction of time period. Phase is, expressed in angle or radian., , 08:56
Page 24 :
Phase difference:, • Phase difference is the difference, between, two waves is having the same frequency and, referenced to the same point in time. It is, expressed in degrees or radians., , 08:56
Page 25 :
Phase difference:, , In Phase (Phase difference = 0), Out of phase (Phase difference not, equal to one), 08:56
Page 26 :
Phase difference:, , Out of Phase, , • Leading, • Lagging, , 08:56
Page 29 :
08:56
Page 30 :
Out of Phase, , 08:56
Page 31 :
i lagging e by an angle 90, , 08:56
Page 32 :
i leading e by an angle 90, , 08:56
Page 33 :
i lagging e by an angle 90, , 08:56
Page 34 :
i leading e by an angle 90, , 08:56
Page 37 :
Analysis of single-phase ac circuits, consisting, 1., 2., 3., 4., 5., 6., , 08:56, , Pure resistance (R), Pure Inductance (L), Pure capacitance (C), Series RL, Series RC, Series RLC
Page 38 :
Analysis of single-phase ac circuits, consisting Pure resistance (R), , 08:56
Page 39 :
Analysis of single-phase ac circuits, consisting Pure resistance (R), , 08:56
Page 40 :
Analysis of single-phase ac circuits, consisting Pure resistance (R), , 08:56
Page 41 :
Analysis of single-phase ac circuits, consisting Pure resistance (R), , • By observing the equations for voltage , it can be, concluded that, the current is in phase with the, voltage., , 08:56
Page 42 :
Analysis of single-phase ac circuits, consisting Pure resistance (R), , •, Phasor Diagram, , 08:56
Page 43 :
Analysis of single-phase ac circuits, consisting Pure resistance (R), , •, , 08:56
Page 44 :
Analysis of single-phase ac circuits, consisting Pure resistance (R), , •, , 08:56
Page 45 :
Analysis of single-phase ac circuits, consisting Pure resistance (R), , 08:56
Page 46 :
Analysis of single-phase ac circuits, consisting Pure resistance (R), , 08:56
Page 47 :
Analysis of single-phase ac circuits, consisting Pure inductance (L), , 08:56
Page 48 :
Analysis of single-phase ac circuits, consisting Pure inductance (L), , 08:56
Page 49 :
Analysis of single-phase ac circuits, consisting Pure inductance (L), , 08:56
Page 50 :
Analysis of single-phase ac circuits, consisting Pure inductance (L), , 08:56
Page 51 :
Analysis of single-phase ac circuits, consisting Pure inductance (L), , 08:56
Page 52 :
Analysis of single-phase ac circuits, consisting Pure inductance (L), , 08:56
Page 53 :
Analysis of single-phase ac circuits, consisting Pure Capacitance (C), , 08:56
Page 54 :
Analysis of single-phase ac circuits, consisting Pure Capacitance (C), , 08:56
Page 55 :
Analysis of single-phase ac circuits, consisting Pure Capacitance (C), , 08:56
Page 56 :
Analysis of single-phase ac circuits, consisting Pure Capacitance (C), , 08:56