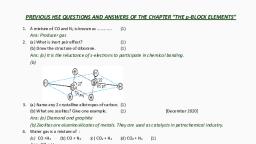
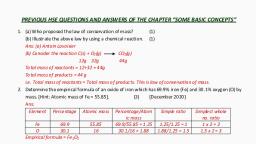
Page 1 :
CHAPTER I, SOME BASIC CONCEPTS OF, CHEMISTRY
Page 2 :
What is chemistry??, , • The branch of science that studies the preparation, properties, structure and, reactions of material substances is called chemistry., , • Chemistry deals with the composition, structure and properties of matter.
Page 3 :
Development of, chemistry, , • People in ancient India, already had the, knowledge of many scientific, phenomenon much before the advent of, modern science., , • In ancient India, chemistry was called, Rasayan Shastra, Rastantra, Ras Kriya or, Rasvidya. It included metallurgy,, medicine, manufacture of cosmetics,, glass, dyes, etc.
Page 4 :
What is common in all…????, •, •, •, •, •, , The Universe…….., The earth……, Different creatures….., , 118 elements…10L compounds....5L carbon compounds...., What is common in all …………..????, , • The 9 alphabets…………., , C, H, E, M, I, S, T, R, Y
Page 5 :
Importance of chemistry, Branches, Of, chemistry, , Inorganic chemistry, , 1, , Rubber technology, , Organic chemistry, , 2, , Nano technology, , Physical chemistry, , 3, , Plastic technology, , Analytical chemistry, , 4, , Food & Drug analysis, , 5, , Metallurgy, , Industrial chemistry
Page 6 :
Nature of matter, Anything which has mass and occupy space is called matter., , •, •, •, •, •, , Matter is classified into physical and chemical substances., Physical substances are further classified into Solids, Liquids and Gases., , Chemical substances are further classified into Pure and Mixture., Pure substances are further classified into Elements and compounds., Mixtures are classified into Homogenous and Heterogenous mixtures.
Page 7 :
Physical classification of matter
Page 8 :
Classification of matter
Page 9 :
Pure substances, Elements and Compounds, Elements are pure substances which, contain same type of atoms., , E.g. : H, He, Li, Be, C etc., Compounds are pure substances, containing different types of atoms or, elements., E.g. : H2O, CO2, NH3, CH4 etc
Page 10 :
Mixtures, • Mixtures: Two or more substances physically combine to form mixtures., • Homogenous mixtures: These are the mixtures in which particles are, uniformly distributed. Eg : salt solution, sugar solution, air, , • Heterogenous mixtures: These are the mixtures in which particles are not, uniformly distributed., , • Eg : Salt and sand mixture, mixtures of salt and sugar.
Page 11 :
The International System of Units, • The International System of Units, (SI) was established by the 11th, General Conference on Weights, and Measures., , • The SI system has seven base units, pertain to the seven fundamental, scientific quantities.
Page 12 :
Prefixes used in the SI system, • The SI system allows the use of, prefixes to indicate the multiples or, submultiples of a unit.
Page 13 :
Mass and Volume, • Mass of a substance is the amount of matter present in it, while weight is the, force exerted by gravity on an object., , • The mass of a substance is constant, whereas, its weight may vary from one, place to another due to change in gravity., , • Volume is the amount of space occupied by a substance., • It has the units of (length)3.
Page 14 :
Density and Temperature, • Density of a substance is its amount, •, •, •, •, , of mass per unit volume. Its unit is kg, m–3 ., Temperature is the measure of degree, of hotness or coldness of a body. 3, scales are generally used, (i) Celsius scale, (ii) Kelvin scale, (iii) Fahrenheit scale., , •, •, , K = 0C + 273.15, F= (9/5 × 0C) +32
Page 15 :
Scientific Notation, Multiplication and Division, , Addition and Subtraction
Page 16 :
Significant figures, Significant figures are meaningful digits which are known with certainty., There are certain rules for determining the number of significant figures. These, are stated below, , All non-zero digits are significant. For example in 285 cm, there are three, significant figures and in 0.25 mL, there are two significant figures., , Zeros previous to first non-zero digit are not significant. Such zero indicates, the position of decimal point. Thus, 0.03 has one significant figure and, 0.0052 has two significant figures.
Page 17 :
Significant figures, Zeros between two non-zero digits are significant. Thus, 2.005 has four, significant figures., , Zeros at the end or right of a number are significant, provided they are on, the right side of the decimal point. For example, 0.200 g has three significant, figures., , Counting the numbers of object, for example, 2 balls or 20 eggs, have, infinite significant figures.
Page 18 :
Precision and Accuracy, • Precision refers to the closeness of, various measurements for the same, quantity., , • Accuracy is the agreement of a, particular value to the true value of, the result.
Page 20 :
Law of Conservation of Mass, , This law was put forth by Antoine Lavoisier in 1789, , According to Lavoisier matter can neither be, created nor destroyed. This is called ‘Law of, Conservation of Mass’.
Page 21 :
Law of Definite Proportions, Joseph Proust, , (1754–1826), , • He stated that a given compound, always contains exactly the same, proportion of elements by weight., , Irrespective of the source a given, compound always contains same elements, combined together in the same proportion, by mass.
Page 22 :
Law of Multiple Proportions, • John Dalton, (1803), , • According to this law, if two elements, , can combine to form more than one, compound, the masses of one element, that combine with a fixed mass of the, other element, are in the ratio of small, whole numbers.
Page 23 :
Gay Lussac’s Law of Gaseous Volumes, Gay Lussac, (1808), , • He observed that when gases combine or, are produced in a chemical reaction they, do so in a simple ratio by volume,, provided all gases are at the same, temperature and pressure.
Page 24 :
Avogadro’s Law, • Lorenzo Romano, , Amedeo Carlo, Avogadro di Quareqa, edi Carreto (1776–1856), , • Avogadro proposed that equal, , volumes of all gases at the same, temperature and pressure should, contain equal number of molecules.
Page 25 :
DALTON’S ATOMIC THEORY, • Matter consists of indivisible atoms., • All atoms of a given element have identical properties, including identical, mass. Atoms of different elements differ in mass., , • Compounds are formed when atoms of different elements combine in a, fixed ratio., , • Chemical reactions involve reorganisation of atoms. These are neither, created nor destroyed in a chemical reaction.
Page 26 :
Atomic Mass, • One atomic mass unit is defined as a mass exactly equal to one-twelfth of the, mass of one carbon - 12 atom.
Page 27 :
Average Atomic Mass, • Many naturally occurring elements, exist as more than one isotope., , • Using these isotopes and their, relative abundance (per cent, occurrence), the average atomic, mass of that element can be, calculated. This is called average, atomic mass.
Page 28 :
Molecular Mass, • Molecular mass is the sum of, atomic masses of the elements, present in a molecule., , • It is obtained by multiplying the, atomic mass of each element by the, number of its atoms and adding, them together.
Page 29 :
Formula Mass, • Some substances, such as, sodium chloride, do not contain, discrete molecules as their, constituent units. In such, compounds, positive (sodium, ion) and negative (chloride ion), entities are arranged in a threedimensional structure., , • Formula mass is the sum of the atomic, masses of all the atoms in a formula, unit of an ionic compound.
Page 30 :
PERCENTAGE COMPOSITION, • Mass % of an element =, , mass of that element in the compound, X 100, molar mass of the compound, , • Percentage composition of elements in water can be written as, • Molar mass of water = 18.02 g, • Mass % of hydrogen =, , • Mass % of oxygen =, , 2𝑋1.008, 18.02, , 16.00, 18.02, , X 100 = 11.18, , X100 = 88.79
Page 31 :
limiting reagent, • In certain reactions one reactant is in more amount than the amount required, by balanced chemical reaction., , • The reactant, which gets consumed first, limits the amount of product, formed and is, therefore, called the limiting reagent., A+B, C+D, If A present 10g and B present 5g then B limits A.
Page 32 :
Balancing a chemical equation, • According to the law of conservation of mass, a balanced chemical equation, has the same number of atoms of each element on both sides of the, equation. Many chemical equations can be balanced by trial and error., , • 4 Fe(s) + 3O2 (g) → 2Fe2O3 (s) balanced equation, • 2 Mg(s) + O2 (g) → 2MgO(s), balanced equation, • P4 (s) + O2 (g) → P4O10(s), unbalanced equation
Page 33 :
Balance the following reaction???
Page 34 :
Empirical Formula for Molecular Formula, • An empirical formula represents the simplest whole number ratio of various, atoms present in a compound., , • Example: CH2Cl, • A molecular formula shows the exact number of different types of atoms, present in a molecule of a compound., , • Example: C2H4Cl2
Page 35 :
Steps involved for finding molecular formula, • Step 1. Conversion of mass per cent to grams, • Step 2. Convert into number moles of each element, • Step 3. Divide each of the mole values obtained above by the smallest, number amongst them, , • Step 4. Write down the empirical formula by mentioning the numbers after, writing the symbols of respective elements, , • Step 5. Writing molecular formula
Page 37 :
Empirical and Molecular, formula, , A compound contains 4.07%, hydrogen, 24.27% carbon, and 71.65% chlorine. Its, molar mass is 98.96 g. What, are its empirical and, molecular formulas?, , Element, , Symbol, , % of, element, , Atomic 𝑃𝑒𝑟𝑐𝑒𝑛𝑡𝑎𝑔𝑒, mass of 𝐴𝑡𝑜𝑚𝑖𝑐 𝑚𝑎𝑠𝑠, element, , Simplest, molar, ratio, , Simplest, whole, number, ratio, , Hydrogen H, , 4.07, , 1, , 4.07, , 2.01, , 2, , Carbon, , C, , 24.27, , 12, , 2.02, , 1, , 1, , Chlorine, , Cl, , 71.65, , 35.5, , 2.02, , 1, , 1, , CH2Cl is, thus, the empirical formula of the above compound.
Page 40 :
Exercise, • Calculate the mass of i)an atom of Silver ii) a molecule of carbon dioxide?, i) 1 mole of Ag atoms = 108g = 6.022×1023 atoms, 6.022×1023 atoms of silver has mass = 108g, 108, , Mass of one atom of Silver = 6.022×1023 = 1.793× 10-22, ii)1 mole of CO2 = 44g, 44, , Mass of 1 molecule of CO2 = 6.022×1023 = 7.307× 10-23
Page 43 :
Concentration of a solution, The concentration of a solution or the amount of substance present in its, given volume can be expressed in any of the following ways., , 1. Mass per cent or weight per cent (w/w %), 2. Mole fraction, 3. Molarity, 4. Molality
Page 45 :
Mole fraction, It is the ratio of number of moles of, a particular component to the total, number of moles of the solution., If a substance ‘A’ dissolves in, substance ‘B’ and their number of, moles are nA and nB , respectively,, then the mole fractions of A and B, are given as
Page 46 :
Molarity, • It is the most widely used unit and, is denoted by M., , • It is defined as the number of, moles of the solute in 1 litre of the, solution., Molarity (M) =, No. of moles of solute, Volume of solution in litres
Page 47 :
Molality, • It is defined as the number of, moles of solute present in 1 kg of, solvent., , • It is denoted by m., • Molality (m) =, , No. of moles of solute, Mass of solvent in kg