Page 1 :
miCene sal, , | 1. Wave Nature of Light: Huygens’ Theory, , There are some phenomena like interference, diffraction, explained by Newton’s corpuscular theory,, Huygen., , a Theassumptions of Huygens’ wave theory are: (i), The locus of particles of a medium vibrating in th, source, the wavefront is spherical; while for a lin, wavefront is plane. (i) Each point of a wavefro, envelope of all wavelets at a given instant gives, , en and polarisation which could not be, These were explained by wave theory first proposed by, , Asource sends waves in all possible directions., € same phase is called a wavefront. For a point, € source the wavefront is cylindrical. A distant, nt acts as a source of secondary wavelets. The, the position of a new wavefront., , . Wavefront, , no, , A wavefront is defined as the locus of all the particles which are vibrating in the same phase. The i, , perpendicular line drawn at any point on the wavefront represents the direction of propagation of, the wave at that point and is called the ‘ray’., , @ Types of Wavefronts: The wavefronts can be of different shapes. In general, we experience |, three types of wavefronts. ;, @ Spherical Wavefront: If the waves in a medium are originating from a point source, then i, they propagate in all directions. If we draw a spherical surface centred at point-source, then, all the particles of the medium lying on that spherical surface will be in the same phase,, because the disturbance starting from the source will reach all these points simultaneously. i, Hence in this case, the wavefront will be spherical and the rays will be the radial lines 5, , [Fig @]. a, , , , E Lm, SOR | vos _ ~, Spherical wavefront eee Plane wavefront, , , , , , Cylindrical wavefront, (a) (b) (c), , ® Cylindrical Wavefront: If the waves in a medium are originating from a line source, then, they too propagate in all directions. In this case the locus of particles vibrating in the same, phase will hea cylindrical surface. Hence in this case the wavefront will be cylindrical. [Fig., , ()), , , , , , Wave Optics | 89, , Scanned with CamScanner
Page 2 :
PEprescints cae press :, , 3. Coherent and Incoherent Sources of Light, , The sources of light emitting waves of same, difference are called coherent sources., , vi per, frequency having 4, , lifference are called incoherent Sources, ase diffe, , a random phase, , ust be coherent, , ndent sou, es, , The sources of light emitting waves with, For interference phenomenon, the sources m, B Methods of Producing Coherent Sources: ©, sources. There are two broad ways of producing, © By division of wavefront: In this method the wall, phase) is divided into two parts. The examples are ‘, @ By division of amplitude: In this method the ae od., , by successive reflections, ¢.g.5 Lloyd's single mirror ™, , rces can never be coheren,, pi at sources foT the same source,, coherent § cof po}, andl t (which is the locus of points of same, efron, , Young's double slit and Fresnel’s biptism,, ‘our s, , ide of a wave, , , , is divided into two party, , 4. Interference of Light light waves ofsame frequency and constant, oO = ~, , Interference is the phenomenon of superposition of tw maximum intensity are called maxima,, phase different travelling in same direction. The positions of ma, while those of minimum intensity are called minima., , @ Conditions of Maxima and Minima: If a, and ay ar, the phase difference at a point under consideration, then, , i i ing waves a i, e amplitudes of interfering waves and 9 is, , Resultant intensity at a point in the region of superposition, T= a} +45 + 2aa,cosh, , =1, +1, + 2/11, cos, , where J, = a; = intensity of one wave, = a; = intensity of other wave, , @ Condition of Maxima:, Phase difference, 6 = 2nz, or path difference, A = ni, n being integer, Maximum amplitude, Aja, = @ + ay, Maximum intensity, J... = AP se = (a, + ay)?, Sap t+a5+2aa,=1,+1+2/11,, , © Condition of Minima: Phase difference, $ = (Qn-1)n, Path difference, A = @n-1)A,n = 1,2,3,., , Minimum amplitude, 4,,;, = (a; ay), , Minimum intensit = 2, Yo Tain (4,~a,) = alta?, , “ht+h-2/Ti, , —2a,a,, , 90 | Physics-XIl: Term-2, , Scanned with CamScanner, , » or constant initial Phase |, coi
Page 3 :
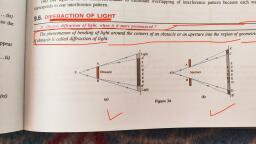
gp Young’s Double Slit Experiment, , Let §, and S, be coherent sources at separation d and D be the, , distance of screen from sources,, then path difference between waves reaching at P, , can be shown as, , For maxima A= nd, , saeiees . . nDA, ©. Position of nth maxima y, = =, , Position of nth minima = (n - 5)s, , @ Fringe width: Fringe width is defined as the separation between, two consecutive maxima or minima., , , , @ Linear fringe width, B = Iati- In = 71, , @ Angular fringe width, By = fo =, , @ Use of white light: When white light is used to illuminate the slit, we obtain an interference, , pattern consisting ofa central white fringe having few coloured fringes on two sides and uniform, illumination., , @ Remark: If waves are of same intensity,, T, = Iy = I (say) then, I= 2, + 2I,cos >, = 21, (1 + cos$), , = 41, cos” 2, , 2, , 5. Diffraction of Light, The bending of light from the corner of small obstacles or apertures is called diffraction of light., @ Diffraction due to a Single Slit:, , When a parallel beam of light is incident normally on a single slit, the beam is diffracted from, the slit and the diffraction pattern consists of a very intense central maximum, and secondary, maxima and minima on either side alternately., , If a is width of slit and @ the angle of diffraction, then the directions of maxima are given by, , asin8 =(n +5) W 3 152,38):, , The position of nth minima are given by, asin @=n\A,, where n = + 1, + 2, + 3, ... for various minima on either side of principal maxima., @ Width of Central Maximum:, The width of central maximum is the separation between the first minima on either side., The condition of minima is, asin @=+mndA (n= 1, 2,3...), The angular position of the first minimum (n= 1) on either side of central maximum is given by, , asin@=+A, => @=+sin (4), , Scanned with CamScanner
Page 4 :
Ds, , Ans., , — A — pal (A, ~. Half-width of central maximum, 8 = sin (2 ), , A, . (A, ©. Total width of central maximum, B = 20 = 2sin (4 ), , lo, , , , , , , , 1, r, 1, 1, ', 1, i, 1, 1, 1, i, 1, 1, 1, 1, 1, 1, 1, ', 1, ‘, t, 1, , 0, , , , 3a., a@ a@ a, , al>, X, 8, , Ae., a a a a, , Diffraction due to a single slit by a monochromatic light, , @ Linear Width: If D is the distance of the screen from slit and y is the distance of nth minima, , from the centre of the principal maxima, then, sin @ = tan8=0 = D, , , , Now,, , nA=asinO@=a0, , An _ In, B= TD, _nAD, z In @, Linear half-width of central maximum, y = =, Total linear width of central maximum, B = = 20D., a, , ELECTED NCERT TEXTBOOK QUESTIONS, , Monochromatic light of wavelength 589 nm is inc} ., the wavelength, pened and esd of () refloctedand Ge air ona water surface, What is, of water is 1.33. refracted light? Refractive index, Given = 589 nm = 589 x 10° m, , Speed of light in air,c = 3 x 10° m/s, , Refractive index of water n,, = 1.33, , (a) The reflected and incident rays are in the same medium so, , seers” ee aS all physical quantities (wavelength,, Wavelength of reflected wave, d= 589 a, Speed of reflected wave, C=3x 198 mi, s, Frequency of reflected wave, veLe 3X 108, 589 x 19-9 ~ 5.1 x 10! Hz, , (b) Refracted wave is in second medium; its frequer, n, , av Cy remain., < times and wavelength changes accordingly Ss unchanged;, , i the speed becomes, , Scanned with CamScanner
Page 5 :
Frequency of refracted wave, v=5.1x 10" Hz, , 3x 108, 1.38, j 8, Wavelength of refracted wave, ate 2.26 X10", vo 5.1.x 10!, = 443 x 10“m = 443 nm, , 9. (a) The refractive index of glass is 1.5, What is the speed of light in glass? (Speed of light in, , = 2.26 x 10° m/s, , , , Speed of refracted wave, v + =, , vacuum is 3.0 x 10° ms" ')., (b) Is the speed of light in glass independent of the colour of light? If not, which of the two, colours, red and violet, travels slower in the glass prism?, Ans. (a) Speed of light in glass,, , ¢ _ 3x10*, , n, 1.5, (b) No, the speed of light in glass depends on the colour of light., , , , = 2x10° m/s, , 1, vos AS Ny > Np “Uy <p, , That is, violet colour travels slower in glass prism., 3. In Young’s double slit experiment the slits are separated by 0.28 mm and the screen is placed, 1.4 m away. The distance between the central bright fringe and the fourth fringe is measured, to be 1.2 cm. Determine the wavelength of light used in this experiment., , Ans. Given d = 0.28 mm = 0.28 x 10°°m,D=14m, , Position of nth bright fringe from central fringe is y, = om, , Here n = 4,94 = 1.2 cm = 1.2 x 10°? m, , 4d _ 1.210") x(0.28%10% m), , = -7 Aes, => Wavelength 4 = 4D al dom =6x107m = 600nm, , , , 4. In Young’s double slit experiment using monochromatic light of wavelength 4 the intensity at, a point on the screen where path difference is 4 is K units. What is the intensity of light at a, , point where path difference is 3?, , Ans. Resultant intensity at any point having a phase difference 6 is given by I= 41, cos” 3, When path difference is 4, phase difference is 2x, [=4I cos? t = 4Iy = K (given) -(i), , When path difference, A= , the phase difference, , geya=> 375, , re Aly cos? oS (since K = Alp), oR_py(LV ab, , K cos Z-xx(5) 4%, , 50 nm and 520 nm, is used to obtain interference, , 5. Abeam of light consisting of two wavelength 6:, y. The separation between, , fringes in a Young’s double slit experiment on a screen 1.2 m awa, the slits is 2mm., , Scanned with CamScanner