Page 1 :
Physics, Model Set – 2, Academic Year: 2020-2021, Date: April 2021, Duration: 3h, , Marks: 70, , 1. The question paper is divided into four sections., 2. Section A: Q. No. 1 contains Ten multiple-choice type of questions carrying One, mark each., 3. Section A: Q. No. 2 contains Eight very short answer type of questions carrying One, mark each., 4. Section B: Q. No. 3 to Q. No. 14 contains Twelve short answer type of questions, carrying Two marks each. (Attempt any Eight)., 5. Section C: Q. No.15 to Q. No. 26 contains Twelve short answer type of questions, carrying Three marks each. (Attempt any Eight)., 6. Section D: Q.No. 27 to Q. No. 31 contains Five long answer type of questions, carrying Four marks each. (Attempt any Three)., 7. Use of log table is allowed. Use of calculator is not allowed., 8. Figures to the right indicate full marks., 9. For each MCQ, correct answer must be written along with its alphabet., e.g., (a) ..... / (b ) .... / ( c ) .... / ( d) ..... Only first attempt will be considered for, evaluation., 10. Physical constants:, a. Latent heat of vaporisation, Lvap = 2256 kJ/kg, b. Acceleration due to gravity, g = 9.8 m/s2, Q. 1 | Select and write the correct answer:, 1. i A diver in a swimming pool bends his head before diving. It ______, 1. Increases his linear velocity, 2. Decreases his angular velocity, 3. Increases his moment of inertia, 4. Decreases his moment of inertia, 1. ii The average energy per molecule is proportional to ______, 1. the pressure of the gas, 2. the volume of the gas, 3. the absolute temperature of the gas
Page 2 :
4. the mass of the gas, 1.iii Heating a gas in a constant volume container is an example of which process?, 1. isochoric, 2. adiabatic, 3. isobaric, 4. cyclic, 1.iv A set of tuning forks is arranged in ascending order of frequencies each tuning fork, gives 8 beats/s with the preceding one. If the frequency of the first tuning fork is 120 Hz, and the last fork is 200 Hz, then the number of tuning forks arranged will be, ______, 1. 8, 2. 9, 3. 10, 4. 11, 1.v If an electron of charge (-e) and mass me revolves around the nucleus of an atom having, an orbital magnetic moment m0, then the angular momentum of the electron is ______, , 1.vi According to De-Broglie, the waves are associated with ______, 1. moving neutral particles only., 2. moving charged particle only., 3. electrons only, 4. all moving matter particles, 1.vii In a Bipolar junction transistor, the largest current flows through ______, 1. in the emitter, 2. in the collector, 3. in the base, 4. through CB junction, 1.viii The moment of inertia of a circular loop of radius R, at a distance of R/2 around a, rotating axis parallel to horizontal diameter of the loop is ______
Page 3 :
1. ½ MR2, 2. ¾ MR2, 3. MR2, 4. 2MR2, Multiple Choice Question., 1.ix. The energy stored in a soap bubble of diameter 6 cm and T = 0.04 N/m is nearly, 1. 0.9 × 10-3 J, 2. 0.4 × 10-3 J, 3. 0.7 × 10-3 J, 4. 0.5 × 10-3 J, 1.x The speed of electron having de Broglie wavelength of 10 -10 m is ______, (me = 9.1 × 10-31 kg, h = 6.63 × 10-34 J-s), 1. 7.28 × 106 m/s, 2. 4 × 106 m/s, 3. 8 × 105 m/s, 4. 5.25 × 105 m/s, Q. 2 | Answer the following:, 2.i On what, the values of absorption coefficient, reflection coefficient, and transmission, coefficient depend, in addition to the material of the object on which the radiation is an, incident?, Ans. The values of absorption coefficient, reflection coefficient, and transmission, coefficient depend on the wavelength of the incident radiation, in addition to the material, of the object on which the radiation is incident., 2.ii Above what temperature, all bodies radiate electromagnetic radiation?, Ans. All bodies at a temperature above 0 K radiate electromagnetic radiation., 2.iii What is the net weight of a body when it falls with terminal velocity through a viscous, medium?, Ans. The net weight of a body when it falls with terminal velocity through a viscous, medium is zero., 2.iv What is the energy associated with the random, disordered motion of the molecules of, a system called as?, Ans. Energy associated with the random, disordered motion of the molecules of a system, called internal energy., 2.v What is the shape of the wavefront on Earth for Sunlight?, Ans. The shape of the wavefront on Earth for Sunlight is a plane.
Page 4 :
2.vi What is the angular momentum of an electron in the first excited state for a hydrogen, atom?, Ans., , 2.viii A solenoid of length 50 cm of the inner radius of 1 cm and is made up of 500 turns of, copper wire for a current of 5 A in it. What will be the magnitude of the magnetic field, inside the solenoid?, Ans. The magnitude of the magnetic field inside the solenoid,, , Q. 3 | Attempt Any Eight:, Derive an expression for maximum safety speed with which a vehicle should move along a, curved horizontal road. State the significance of it., Ans., i. Consider a vertical section of a car moving on a horizontal circular track having a, radius ‘r’ with ‘C’ as the centre of the track., , ii., , Forces acting on the car (considered to be a particle):, a. Weight (mg), vertically downwards,, b. Normal reaction (N), vertically upwards that balances the weight, c. Force of static friction (fs) between the road and the tyres., Since normal reaction balances the weight, ∴ N = mg ….(1)
Page 5 :
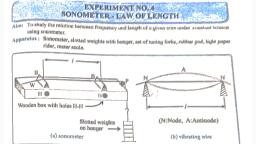
While working in the frame of reference attached to the vehicle, the frictional force, balances the centrifugal force., , i., ii., , This is an expression of maximum safety speed with which a vehicle should move, along a curved horizontal road., Significance: The maximum safe speed of a vehicle on a curve road depends upon, friction between tyres and road, the radius of the curved road and acceleration due, to gravity., , Q. 4 For a stationary wave set up in a string having both ends fixed, what is the ratio of the, fundamental frequency to the third harmonic?, Ans., , Q. 5 How the frequency of the vibrating wire is affected if the load is fully immersed in, water?
Page 6 :
Ans. According to the law of tension of a vibrating string, the fundamental frequency (n) is, directly proportional to the square root of its tension. [when l and m are kept constant], , i., , If the load is fully immersed in water, the tension in the string decreases. Hence, the, frequency of vibration also decreases., , Q. 6 What are the disadvantages of a potentiometer over a voltmeter?, Ans., i. The potentiometer is not portable., ii. Direct measurement of potential difference or emf is not possible., Q. 7 Distinguish between an ammeter and a voltmeter., Ans., , Q. 8 Define magnetization. State its SI unit and dimensions., Ans., i. The ratio of magnetic moment to the volume of the material is called magnetization., ii. Unit: Am-1 in SI system., iii. Dimensions: [M0L-1T0I1], Q. 9 Draw a neat labelled circuit diagram of a full-wave rectifier using a semiconductor, diode., Ans. Full-wave rectifier:
Page 7 :
Q. 10 3 mole of a gas at temperature 400 K expands isothermally from an initial volume of, 4 litres to a final volume of 8 litres. Find the work done by the gas. (R = 8.31 J mol-1 K-1), Ans. Given:, n = 3 mol, T = 400 K, Vi = 4 L, Vf = 8 L, R = 8.31 J mol-1 K-1, To find: Work done by gas (W)
Page 8 :
Q. 11 The acceleration due to gravity on the surface of the moon is 1.7 m/s2. What is the, time period of a simple pendulum on the surface of the moon if its time period on the, surface of the earth is 3.5 s? (g on the surface of earth = 9.8 m/s2), Ans. Given: gm = 1.7 m/s2, gE = 9.8 m/s2, TE = 3.5 s, To find: Time period on the surface of the moon (Tm), , The time period of a simple pendulum on the surface of the moon is 8.4 s., Q. 12 Currents of equal magnitude pass through two long parallel wires having a, separation of 1.35 cm. If the force per unit length on each of the wires is 4.76 x 10-2 N/m,, what is I?
Page 9 :
Ans., , Q. 13 If the total energy of radiation of frequency 1014 Hz is 6.63 J, Calculate the number of, photons in the radiation., Ans. Given:, E = 6.63 J, ν = 1014 Hz,, We know, h = 6.63 × 10–34 Js., To find: Number of photons (n), , Q. 14 Draw the circuit symbol for NPN and PNP transistors. What is the difference in the, Emitter, Base, and Collector regions of a transistor?, Ans. The circuit symbols of the two types of transistors:
Page 10 :
Figure (a), , Figure (b), The difference in the Emitter (E), the Base (b), and the Collector (C) are as follows:, i., ii., iii., , Emitter: It is a thick heavily doped layer. This supplies a large number of majority, carriers for the current flow through the transistor, Base: It is the thin, lightly doped central layer., Collector: It is a thick and moderately doped layer. Its area is larger than that of the, emitter and the base. This layer collects a major portion of the majority of carriers, supplied by the emitter. The collector also helps dissipation of any small amount of, heat generated., , Q. 15 | Attempt Any Eight:, State Stoke’s law and give two factors affecting angle of contact., Ans. Statement: The viscous force acting on a small sphere falling through a medium is, directly proportional to the radius (r) of the sphere, its velocity (v) through fluid, and, coefficient of viscosity (η) of the fluid., Two factors affecting the angle of contact:, i., ii., , The nature of the liquid and the solid in contact., Impurities present in the liquid change the angle of contact., , Q. 16 Answer in brief:, Obtain the expression for the period of a magnet vibrating in a uniform magnetic field and, performing S.H.M.
Page 11 :
Ans. A, , Time period of an oscillation body about a fixed point can be defined as the time taken by, the body to complete one vibration around that particular point is called time period., Ans. B, i. If a bar magnet is freely suspended in the plane of a uniform magnetic field, it, remains in equilibrium with its axis parallel to the direction of the field., If it is given a small angular displacement θ about an axis passing through its centre,, perpendicular to itself and to the field and released, it performs angular oscillations., ii. Let μ be the magnetic dipole moment and B the magnetic field. In the deflected, position, a restoring torque acts on the magnet that tends to bring it back to its, equilibrium position.
Page 12 :
iii., iv., , i., ii., , Magnet vibrating in a uniform magnetic field, The magnitude of this torque is τ = µBsinθ, If θ is small, sinθ ≈ θ, ∴ τ = µBθ, For clockwise angular displacement θ, the restoring torque is in the anticlockwise, direction., ∴ τ = Iα = –μBθ, Where I is the moment of inertia of the bar magnet and α is its angular acceleration., , Since µ, B, and I are constants, equation (1) shows that angular acceleration is, directly proportional to the angular displacement and directed opposite to the, angular displacement. Hence the magnet performs angular S.H.M., The period of vibrations of the magnet is given by,, , Q. 17 Explain experimental setup for Fraunhofer diffraction with neat diagram., Ans.
Page 13 :
i., ii., iii., , iv., , Set up for Fraunhofer diffraction has a monochromatic source of light S at the focus, of a converging lens. Ignoring aberrations, the emerging beam will consist of plane, parallel rays resulting in-plane wavefronts., These are incidents on the diffracting element such as a slit, a circular aperture, a, double slit, a grating, etc., In the case of a circular aperture, S is a point source and the lenses are bi-convex., For linear elements like slits, grating, etc., the source is linear and the lenses are, cylindrical in shape so that the focussed image is also linear., , Set up for Fraunhofer diffraction, An emerging beam is an incident on another converging lens that focuses the beam, on a screen., , Q.18 Explain step up and step down transformer?, Ans., i. Step-up transformer:, a. A transformer that converts a low voltage at high current into a high voltage at, low current is called a step-up transformer., b. In a step-up transformer, the number of turns in secondary coil NS is greater than, the number of turns in primary coil NP. In this transformer, eS > eP and IS < IP., c. The primary coil is made from a thick insulated copper wire so that it can sustain, the high current. The secondary coil is made of a thin insulated wire., d. Current through secondary is less than primary., ii. Step down transformer:, a. A transformer which converts a high voltage at low current into a low voltage at, high current is called a step-down transformer., b. In step down transformer, the number of turns in the secondary coil NS is less, than the number of turns in the primary coil NP. In this transformer eS < eP and IS >, IP., c. The primary coil is made of a thin insulated wire and the secondary coil is made, from thick wire so that it can sustain the high current., d. Current through primary is less than secondary., Q. 19 Obtain an expression for the energy stored in a charged condenser. Express it in, different forms., Ans.
Page 14 :
i., , ii., , Consider a capacitor of capacitance C being charged by a DC source of V volts as, shown in the figure below., , A capacitor charged by a DC source, During the process of charging, let q' be the charge on the capacitor and V be the, potential difference between, , This work done is stored as electrical potential energy U of the capacitor. This work done, can be expressed in different forms as follows., , Q. 20 Explain Biot Savart's Law., Ans., i., Consider an arbitrarily shaped wire carrying a current I., ii. Let dl be a length element along the wire. The current in this element is in the, direction of the length vector dldl→ which produces differential magnetic, field dBdB→ directed into the plane of the paper as shown in the figure below:
Page 15 :
iii., , Current carrying wire of arbitrary shape, Consider point P at distance r from element dl. The net magnetic field at point P can, be obtained by integrating i.e., summing up of magnetic fields dBdB→ from these, length elements., , Q. 22 A radio can tune over the frequency range of a portion of the MW broadcast band, (800kHz -1200kHz). If its LC circuit has an effective inductance of 200mH, what must be, the range of its variable condenser?, Ans. Given:, f1 = 800 kHz = 0.8 × 106 Hz, f2 = 1200 kHz = 1.2 × 106 Hz, L = 200 mH = 200 × 10-3 = 0.2 H, To find: Range of condenser
Page 16 :
Q. 23 In Fraunhoffer diffraction by a narrow slit, a screen is placed at a distance of 2 m, from the lens to obtain the diffraction pattern. If the slit width is 0.2 mm and the first, minimum is 5 mm on either side of the central maximum, find the wavelength of light., Ans. A Data: D = 2 m, y1d = 5 mm = 5 × 10-3 m,, a = 0.2 mm = 0.2 × 10-3 m = 2 × 10-4 m
Page 17 :
Ans. B Given:, D = 2 m, a = 0.2 mm = 2 × 10-4 m, y1d = 5 mm, Width of central maxima = 2y1d = 2 × 5 mm, = 10 mm = 10 × 10-3 m, To find: Wavelength of light (λ), , Wavelength of the light used is 5000 Å., Q. 24 Two parallel plate capacitors X and Y have the same area of the plates and the same, separation between them is connected in series to a battery of 15 V. X has air between the, plates while Y contains a dielectric of constant k = 2., i) Calculate the capacitance of each capacitor if the equivalent capacitance of the, combination is 2 μF., ii) Calculate the potential difference between the plates of X and Y.
Page 18 :
iii) What is the ratio of the electrostatic energy stored in X and Y?, Ans. Given: V = 15 volt, kX = 1, kY = 2, Cs = Ceq = 2 μF
Page 20 :
i., ii., iii., , Capacitance of each capacitor are 3 μF and 6 μF., The potential difference between the plates of X and Y is 10 V and 5 V respectively., The ratio of electrostatic energy stored in X and Y is 2:1., , Q. 25 A cylinder containing one gram molecule of the gas was compressed adiabatically, until its temperature rose from 27°C to 97°C. Calculate the work done and heat produced in, the gas (𝛾 = 1.5)., Ans. Given:, n = 1, 𝛾 = 1.5, Tf - Ti = 97 - 27 = 70°C, We know, R = 8.31 J/mol K, To find:, i., ii., , Work done (W), Heat produced (Q), , i., ii., , Work done is -11.63 × 102 J, The heat produced in the gas 278 cal., , Q. 26 A flywheel of mass 8 kg and radius 10 cm rotating with a uniform angular speed of 5, rad/sec about its axis of rotation, is subjected to an accelerating torque of 0.01 Nm for 10, seconds. Calculate the change in its angular momentum and change in its kinetic energy., Ans. Given:, M = 8 kg, R = 10 cm = 0.1 m,, ω1 = 5 rad/s, τ = 0.01 Nm, t = 10 s
Page 21 :
To find:, i., ii., , Change in angular momentum (∆L), Change in K.E. (∆K.E.), , The change in its angular momentum and change in its kinetic energy is 0.1 kg m2/s, and 0.625 J respectively., Q. 27 | Attempt Any Three:
Page 22 :
27.i Derive Laplace’s law for spherical membrane of bubble due to surface tension., Ans. A Consider a spherical liquid drop and let the outside pressure be Po and inside, pressure be Pi, such that the excess pressure is Pi − Po, , Let the radius of the drop increase from r to Δr, where Δr is very small, so that the pressure, inside the drop remains almost constant., , This work done is equal to the product of the force and the distance Δr., dF=(P1 - P0)4πr2
Page 23 :
The increase in the radius of the bubble is Δr., , This is called Laplace’s law of spherical membrane., Ans. B, , i., , ii., iii., iv., , v., vi., , The free surface of drops or bubbles is spherical in shape., Let,, Pi = inside pressure of a drop or air bubble, Po = outside pressure of the bubble, r = radius of drop or bubble., As drop is spherical, Pi > Po, ∴ excess pressure inside drop = Pi − Po, Let the radius of drop increase from r to r + ∆r so that inside pressure remains, constant., Initial area of drop A1 = 4πr2 ,, Final surface area of drop A2 = 4π (r + ∆r)2, Increase in surface area,, ∆A = A2 − A1 = 4π[(r + ∆r)2 − r2], = 4π[r2 + 2r∆r + ∆r2 − r2], = 8πr∆r + 4π∆r2, As ∆r is very small, the term containing ∆r2 can be neglected., ∴ dA = 8πr∆r, Work is done by a force of surface tension,, dW = TdA = (8πr∆r)T ….(1), This work done is also equal to the product of the force F which causes an increase, in the area of the bubble and the displacement Δr which is the increase in the radius, of the bubble., ∴ dW = FΔr, The excess force is given by,, (Excess pressure) × (Surface area), ∴ F = (Pi – Po) × 4πr2, ∴ dF = (Pi – Po)A, dW = F∆r = (Pi − Po) A∆r
Page 24 :
From equation (1),, (Pi − Po) A∆r = (8πr∆r) T, , Equation (2) represents Laplace’s law of spherical membrane., 27.ii Show that half life period of radioactive material varies inversely to decay constant λ., Ans. From law of radioactive decay,, , Q. 28 Derive Mayer’s relation., Ans., i. Consider one mole of an ideal gas that is enclosed in a cylinder by a light, frictionless, airtight piston., ii. Let P, V, and T be the pressure, volume, and temperature respectively of the gas., iii. If the gas is heated so that its temperature rises by dT, but the volume remains, constant, then the amount of heat supplied to the gas (dQ1) is used to increase the, internal energy of the gas (dE). Since the volume of the gas is constant, no work is, done in moving the piston., ∴ dQ1 = dE = CV dT ..............(1), where CV is the molar specific heat of the gas at constant volume.
Page 25 :
iv., , i., ii., iii., , iv., v., , On the other hand, if the gas is heated to the same temperature, at constant, pressure, the volume of the gas increases by an amount say dV. The amount of heat, supplied to the gas is used to increase the internal energy of the gas as well as to, move the piston backward to allow expansion of gas. The work is done to move the, piston dW = PdV., ∴ dQ2 = dE + dW = Cp dT ..............(2), Where CP is the molar specific heat of the gas at constant pressure., From equations (1) and (2),, ∴ Cp dT = CV dT + dW, ∴ (Cp - Cv)dT = PdV ..............(3), For one mole of gas,, PV = RT, ∴ P dV = R dT, since pressure is constant., Substituting equation (3), we get, (Cp - Cv) dT = R dT, ∴ Cp - Cv = R, This is known as Mayer’s relation between CP and CV., Also, CP = M0SP and CV = M0SV, where M0 is the molar mass of the gas and SP and, SV are respective principal specific heats. Thus, M0SP - M0SV = R/J, Where J is the mechanical equivalent of heat., , 29.i Distinguish between a potentiometer and a voltmeter., Ans. A, Potentiometer, , Voltmeter, , 1., , A potentiometer is used to determine the, emf of a cell, potential difference, and, internal resistance., , A voltmeter can be used to measure the, potential difference and terminal voltage of, a cell. But it cannot be used to measure the, emf of a cell., , 2., , Its accuracy and sensitivity are very high., , Its accuracy and sensitivity are less as, compared to a potentiometer., , 3., , It is not a portable instrument., , It is a portable instrument., , 4., , It does not give a direct reading., , It gives a direct reading., , Ans. B, No., i., , Potentiometer, Its resistance is infinite., , Voltmeter, Its resistance is high but finite.
Page 26 :
ii., , It does not draw any current from the, source of known e.m.f., , It draws some current from the source, of e.m.f., , iii., , The potential difference measured by it is, equal to the actual potential difference, (p.d.)., , The potential difference measured by it, is less than the actual potential, difference (p.d.)., , iv., , It has high sensitivity., , It has low sensitivity., , v., , It measures e.m.f as well as p.d., , It measures only p.d., , vi., , It is used to measure the internal, resistance of a cell., , It cannot be used to measure the, internal resistance of a cell., , vii. It is more accurate., , It is less accurate., , viii. It does not give a direct reading., , It gives a direct reading., , ix., , It is not portable., , It is portable., , x., , It is used to measure lower voltage values, only., , It is used to measure lower as well as, higher voltage values., , 29.ii An iron rod of the area of cross-section 0.1m2 is subjected to a magnetizing field of, 1000 A/m. Calculate the magnetic permeability of the iron rod. [Magnetic susceptibility of, iron = 59.9, magnetic permeability of vacuum = 4π x 10-7 S. I. unit], Ans. A, Given:- H= 1000 A/m, χ = 59.9, μ0 = 4π x 10-7 S.I. unit, To find:- Permeability (μ), Formula:- μ = μ0 (1 + χ), Calculation:- From formula,, μ = 4π x 10-7 (1 + 59.9), = 4 x 3.142 x 10-7 x 60.9, = antilog [log(4) + log(3.142) + log(60.9)] x 10-7, = antilog [0.6021 + 0.4972 + 1.7846] x 10-7, = antilog [2.8839] x 10-7, = 765.4 x 10-7, ∴ μ = 7.654 x 10-5 Wb/A-m, The magnectic permeability of the iron rod is 7.654 x 10-5 Wb/A-m., Ans. B Given:
Page 27 :
H = 1000 A/m, χ = 599,, μ0 = 4π × 10-7 S.I. unit, To find: Permeability (μ), Formula: μ = μ0(1 + χ), Calculation:, From formula,, μ = 4π × 10-7 (1 + 599), = 4 × 3.142 × 10-7 × 600, ∴ μ = 7.54 × 10-4 Hm-1, The magnetic permeability of the iron rod is 7.54 × 10-4 Hm-1., 30.i Why and where are eddy currents are undesirable? How are they minimized?, Ans. Undesirable effects of eddy currents:, The soft iron core is used in dynamo transformers, motors, generators, etc. When a.c is, passed through these instruments the flux changes and eddy currents are set up in the, core. Therefore, the core is heated up so the electrical energy is wasted in the form of heat, energy., Minimization of the undesirable effect of eddy current:, i., ii., , To minimize the undesirable effect of eddy currents, laminated or insulated iron, core is used which minimizes the magnitude of eddy currents., If the surface area of the metal plate is reduced, amount of eddy current generated is, reduced., , 30.ii Calculate De Broglie's wavelength of the bullet moving with speed 90m/sec and, having a mass of 5 gm., Ans. Given: v = 90 m/s, m = 5 g, To find: De Broglie wavelength (λ), , De Broglie wavelength of given bullet is 1.473 × 10-36 m.
Page 28 :
31.i Obtain an expression for the self-inductance of a solenoid., Ans., i. Consider a current I established in the windings (turns) of a long solenoid. The, current produces a magnetic flux BϕB through the central region., ii. The inductance of the solenoid is given by,, , i., ii., , iii., , where N = the number of turns,, ΦB = magnetic flux linkage., The flux linkage for a length l near the middle of the solenoid is,, , where n = the number of turns per unit length,, B = magnetic field, A = the cross-sectional area of the solenoid., , where, Al is the interior volume of solenoid., 31.ii The angular momentum of an electron in the 3rd Bohr orbit of a Hydrogen atom is, 3.165 × 10-34 kg m2/s. Calculate Plank’s constant h., Ans. Given: L3 = 3.165 × 10-34 kg m2/s, n = 3, To find: Planck’s constant (h)
Page 29 :
= 6.284 × 1.055 × 10−34, = antilog {log(6.284) + log(1.055)} × 10−34, = antilog {0.7982 + 0.0232} × 10−34, = antilog{0.8214} × 10−34, = 6.628 × 10−34 Js, The value of Planck’s constant (h) is 6.628 × 10–34 Js.