Page 1 :
Physics, Model Set-1, Academic Year: 2020-2021, Date: April 2021, Duration: 3h, , Marks: 70, , 1. The question paper is divided into four sections., 2. Section A: Q. No. 1 contains Ten multiple-choice type of questions carrying One, mark each., 3. Section A: Q. No. 2 contains Eight very short answer type of questions carrying One, mark each., 4. Section B: Q. No. 3 to Q. No. 14 contains Twelve short answer type of questions, carrying Two marks each. (Attempt any Eight)., 5. Section C: Q. No.15 to Q. No. 26 contains Twelve short answer type of questions, carrying Three marks each. (Attempt any Eight)., 6. Section D: Q.No. 27 to Q. No. 31 contains Five long answer type of questions, carrying Four marks each. (Attempt any Three)., 7. Use of log table is allowed. Use of calculator is not allowed., 8. Figures to the right indicate full marks., 9. For each MCQ, correct answer must be written along with its alphabet., e.g., (a) ..... / (b ) .... / ( c ) .... / ( d) ..... Only first attempt will be considered for, evaluation., 10. Physical constants:, a. Latent heat of vaporisation, Lvap = 2256 kJ/kg, b. Acceleration due to gravity, g = 9.8 m/s2, , Q.1 | Select and write the correct answer:, 1.i Which of the following is correct, when the energy is transferred to a system from its, environment?, 1. System gains energy, 2. System loses energy, 3. System releases energy, 4. the system does not exchange energy, 1.ii For work done to be reversible, the process should be ______, 1. cyclic, 2. isobaric, 3. isochoric, 4. adiabatic
Page 2 :
1.iii A particle is performing simple harmonic motion with amplitude A and angular, velocity ω. the ratio of maximum velocity to maximum acceleration is ______, 1. ω, 2. I/ω, 3. ω2, 4. A/ω, 1.iv In the law of tension, the fundamental frequency of the vibrating string is, ______, 1. inversely proportional to the square root of tension, 2. directly proportional to the square of tension, 3. directly proportional to the square root of tension, 4. inversely proportional to the density, 1.v The integral multiple of fundamental frequencies are ______, 1. beats, 2. resonance, 3. overtones, 4. harmonics, 1.vi A LED emits visible white light when its ______, 1. junction is reversed biased, 2. depletion layer widens, 3. holes and electrons recombine, 4. junction becomes hot, 1.vii Insect moves over the surface of water because of ______, 1. Elasticity, 2. Surface tension, 3. Friction, 4. Viscosity, 1.viii Two capillary tubes of radii 0.6 cm and 0.3 cm are dipped in the same liquid. The, ratio of heights through which the liquid will rise in the tubes is ______, 1. 2:1, 2. 1:2, 3. 4:1, 4. 1:4, 1.ix Light of wavelength 5000 A.U. falls on a plane reflecting surface. The frequency of, reflected light is ______, 1. 6 × 1014Hz, 2. 5 × 1014Hz, 3. 2 × 1014Hz, 4. 1.666 × 1014Hz
Page 3 :
1.x You are given a number of capacitors labelled as 8μF - 250V. Find the number of, capacitors needed to get an arrangement equivalent to 16μF - 1000V., 1. 4, 2. 16, 3. 32, 4. 64, Q.2 | Answer the following:, 2.i What are cohesive forces?, Ans. The force of attraction between the molecules of the same substance is called cohesive, force., 2.ii Under which condition laws of Boyle, Charles, and Gay-Lussac are valid?, Ans. The laws of Boyle, Charles, and Gay-Lussac are strictly valid for real gases, only if the, pressure of the gas is not too high and the temperature is not close to the liquefaction, temperature of the gas., 2.iii When two objects are said to be in thermal equilibrium?, Ans. When two objects are at the same temperature, they are in thermal equilibrium., 2.iv A simple pendulum moves from one end to the other in ¼ second. What is its, frequency?, Ans., , 2.v What is the basis of Kirchhoff’s current law and voltage law?, Ans., i. Kirchhoff’s current law is based on the law of conservation of charge., ii. Kirchhoff’s voltage law is based on the law of conservation of energy.
Page 4 :
2.vi What does the ratio of magnetization to magnetic intensity indicate?, Ans. The ratio of magnetization to magnetic intensity indicates magnetic susceptibility (χ)., 2.vii A square metal plate of area 100 cm2 moves parallel to another plate with a velocity of, 10 cm/s, both plates immersed in water. If the viscous force is 200 dyne and the viscosity, of water is 0.01 poise, what is the distance between them?, Ans., , 2.viii What do you mean by dielectric polarization?, Ans. Dielectric polarization is the term given to describe the behavior of a material when, an external electric field is applied to it. It occurs when a dipole moment is formed in an, insulating material because of an externally applied electric field., Q. 3 | Attempt Any Eight:, A flywheel is revolving with a constant angular velocity. A chip of its rim breaks and flies, away. What will be the effect on its angular velocity?, Ans., i. When the chip of the rim of a flywheel revolving with a constant angular velocity, breaks away, its mass will decrease., ii. Due to the decrease in its mass, the moment of inertia of the flywheel will decrease., iii. In order to conserve angular momentum, the angular velocity of the flywheel will, increase., Q. 4 Draw a p-V diagram of the reversible process., Ans. p-V diagram of the reversible process:
Page 5 :
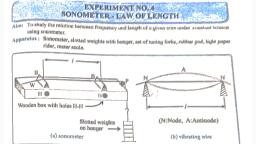
Q. 5 Draw a p-V diagram showing negative work with varying pressure., Ans. p-V diagram showing negative work with varying pressure:, , Q. 6 Distinguish between an overtone and harmonic., Ans., Sr., No., , Overtone, , Harmonic, , i., , The first harmonic is the, The first overtone is the next higher frequency of, natural frequency of vibration. vibration., , ii., , Harmonics are simply integral Overtones are not necessarily integral multiples of, multiples of the fundamental the fundamental frequency. They are frequencies, frequency., other than the fundamental frequency., , iii., , All harmonics may or may not, All overtones are always present in the vibration., be present in vibration, , Q. 7 What are stationary waves? Why are they called stationary waves?, Ans., i. When two identical waves traveling along the same path in opposite directions, interfere with each other, the resultant wave is called a stationary wave., ii. Stationary waves are called so because the resultant harmonic disturbance of the, particles does not travel in any direction and there is no transport of energy., Q. 8 Draw a neat labelled diagram of a schematic of the experimental setup for the, photoelectric effect., Ans. Schematic of experimental set-up for photoelectric effect:
Page 6 :
Q. 9 State any two advantages and disadvantages of a photodiode., Ans. Advantages of photodiode:, i., ii., iii., iv., v., vi., , Quick response when exposed to light., The reverse current is linearly proportional to the intensity of incident light. (Linear, response), High speed of operations., Lightweight and compact size., Wide spectral response. E.g., photodiodes made from silicon respond to radiation of, wavelengths from 190 nm (UV) to 1100 nm (IR)., Relatively low cost., , Disadvantages of photodiode:, i., ii., , Its properties are temperature-dependent, similar to many other semiconductor, devices., Low reverse current for low illumination levels., , Q. 10 The moment of inertia of a body about a given axis is 1.2 kgm2. initially, the body is at, rest. For what duration on the angular acceleration of 25 radian/sec2 must be applied, about that axis in order to produce rotational kinetic energy of 1500 joule?, Ans.
Page 7 :
Q. 11 1000 calories of radiant heat are incident on a body. If the body absorbs 400 calories, of heat, find the coefficient of emission of the body., Ans.
Page 8 :
Q. 12 Four resistances 6Ω, 6Ω, 6Ω and 18Ω form a Wheatstone bridge. Find the resistance, which connected across the 18Ω resistance will balance the network., Ans.
Page 9 :
Q. 13 The magnetic flux through a loop varies according to the relation Φ = 8t2 + 6t + 2, Φ is, in milliweber and t is in second. What is the magnitude of the induced emf in the loop at t =, 2 seconds?, Ans.
Page 10 :
Q. 14 Define current amplification factor αDC and βDC Obtain the relation between them., Ans.
Page 11 :
Q. 15 | Attempt Any Eight:, Derive an expression for the kinetic energy of a rotating body with uniform angular, velocity., Ans., i. Consider a rigid object rotating with a constant angular speed ω about an axis, perpendicular to the plane of the paper., , A body of N particles, For theoretical simplification, let us consider the object to be consisting of N, particles of masses m1, m2, …..mN at respective perpendicular distances r1, r2,, …..rN from the axis of rotation., iii. As the object rotates, all these particles perform UCM with the same angular speed, ω, but with different linear speeds,, v1 = r1ω, v2 = r2ω,…., vN = rNω, ii.
Page 12 :
Q. 16 Explain the phenomena of surface tension on the basis of molecular theory., Ans. Molecular theory of surface tension:, i., ii., iii., iv., , v., , vi., , Let PQRS = Surface film of liquid in a container containing liquid. PS is the free, surface of the liquid and QR is the inner layer parallel to PS at distance equal to the, range of molecular force., Now consider three molecules A, B, and C in a liquid in a vessel such that molecule A, is well inside the liquid, molecule B within the surface film, and molecule C is on the, surface of the liquid as shown in the figure., The sphere of influence of molecule A is entirely inside the liquid. As a result,, molecule A is acted upon by equal cohesive forces in all directions. Thus, the net, cohesive force acting on molecule A is zero., For molecule B, a large part of its sphere of influence is inside the liquid and a, smaller part is outside the surface (in the air). The adhesive force acting on molecule, B due to air molecules above it and within its sphere of influence is weak compared, to the strong downward cohesive force acting on the molecule. As a result, molecule, B gets attracted inside the liquid., For molecule C, half of the sphere of influence is in air and half is in liquid. As the, density of air is much less than that of liquid, the number of air molecules within the, sphere of influence of molecule C above the free surface of the liquid is much less, than the numbers of liquid molecules within the sphere of influence that lies within, the liquid. Thus, the adhesive force due to the air molecules acting on molecule C is, weak compared to the cohesive force acting on the molecule. As a result, molecule C, also gets attracted inside the liquid., Thus, all molecules in the surface film are acted upon by an unbalanced net cohesive, force directed into the liquid. Therefore, the molecules in the surface film are pulled, inside the liquid. This minimizes the total number of molecules in the surface film., As a result, the surface film remains under tension. The surface film of a liquid
Page 14 :
(superposition) of two linear S.H.M.s of the same period and occurring along the, same path is also an S.H.M., , Q. 18 Explain the reflection of light at a plane surface with the help of a neat ray diagram., Ans., , Reflection of light, XY: Plane reflecting surface, AB: Plane wavefront, RB1: Reflecting wavefront, A1M, B1N: Normal to the plane, ∠AA1M = ∠BB1N = ∠i = Angle of incidence, ∠TA1M = ∠QB1N = ∠r = Angle of reflection, Explanation:, i. A plane wavefront AB is advancing obliquely towards the plane reflecting surface XY., AA1 and BB1 are incident rays.
Page 15 :
ii. When ‘A’ reaches XY at A1, then the ray at ‘B’ reaches point ‘P’ and it has to cover distance, PB1 to reach the reflecting surface XY., iii. Let ‘t’ be the time required to cover distance PB1. During this time interval, secondary, wavelets are emitted from A1 and will spread over a hemisphere of radius A1R, in the same, medium. Distance covered by secondary wavelets to reach from A1 to R in time t is the, same as the distance covered by primary waves to reach from P to B1. Thus A1R = PB1 = ct., iv. All other rays between AA1 and BB1 will reach XY after A1 and before B1. Hence, they will, also emit secondary wavelets of decreasing radii., v. The surface touching all such hemispheres is RB1 which is reflected wavefront, bounded, by reflected rays A1R and B1Q., vi. Draw A1M ⊥ XY and B1N ⊥ XY., Thus, angle of incidence is ∠AA1M = ∠BB1N = i and angle of reflection is ∠MA1R = ∠NB1Q =, r., ∴ ∠RA1B1 = 90 - r and ∠PB1A1 = 90 - i, vii. In ΔA1RB1 and ΔA1PB1, ∠A1RB1 ≅ ∠A1PB1, A1R = PB1 (Reflected waves travel equal distance in the same medium in equal time)., A1B1 = A1B1 ….(common side), ∴ ΔA1RB1 ≅ ΔA1PB1, ∴ ∠RA1B1 = ∠PB1A1, ∴ 90 - r = 90 - i, ∴i=r, viii. Also, from the figure, it is clear that incident ray, reflected ray, and normal lie in the, same plane., ix. Assuming rays AA1 and BB1 to be coming from extremities of the object, A1B1 is the size, of the object. Distance between corresponding reflected rays A1T and B1Q will be the same, as A1B1 as they are corresponding parts of congruent triangles. This implies the size of the, object in a reflected image is the same as the actual size of an object., x. Also, taking A and B to be right and left sides of the object respectively, after reflection, right side at A is seen at T and left side at B is seen at Q. This explains lateral inversion., Q. 19 Describe Young’s double-slit experiment with a neat diagram showing points of, maximum and minimum intensity., Ans., i., , In Young’s double-slit interference experiment, a plane wavefront is made to fall on, an opaque screen AB having two similar narrow slits S1 and S2.
Page 16 :
ii., , iii., iv., v., vi., vii., viii., ix., x., , The figure below shows a cross-section of the experimental setup and the slits have, their lengths perpendicular to the plane of the paper., , Young’s double-slit experiment, The slits are about 2 - 4 mm apart from each other., An observing screen PQ is placed behind AB., Assuming that the slits S1 and S2 are equidistant from the S, the wavefronts starting, from S and reaching the S1 and S2 at every instant of time are in phase., When the rays fall on S1 and S2, the two slits act as secondary sources of lightemitting cylindrical wavelets (with axis along the slit length) to the right of AB., The two secondary sources emit waves in phase with each other., The crests/troughs of the secondary wavelets superpose as shown in the figure and, interfere constructively high intensity giving rise to a bright band., When the crest of one wave coincides with the trough of the other causing zero, intensity, dark images of the slits are produced on the screen PQ., The dark and bright regions are called fringes and the whole pattern is called an, interference pattern., , Q. 20 Explain the construction and working of the Moving coil Galvanometer., Ans. Construction:, i. M.C.G. consists of a coil of several turns mounted (suspended or pivoted) in such a, way that it can freely rotate about a fixed axis, in a radial uniform magnetic field.
Page 17 :
ii., , A soft iron cylindrical core makes the field radial and strong., , Moving coil galvanometer, Working:, i., , ii., , The coil rotates due to a torque acting on it as the current flows through it. The, torque acting on the current-carrying coil is τ = NIAB sinθ., Here θ = 90° as the field is radial., ∴ τ = NIAB, where A is the area of the coil, B the strength of the magnetic field, N the number of, turns of the coil, and I the current in the coil., This torque is counter balanced by a torque due to a spring fitted at the bottom so, that a fixed steady current I in the coil produces a steady angular deflection Φ., , Q. 21 Explain the term inductive reactance. State its unit and dimensions., Ans.
Page 18 :
Q. 22 An alternating emf of 230V, 50Hz is connected across a pure ohmic resistance of 50Ω., Find (1) the current (2) equations for instantaneous values of current and voltage., Ans.
Page 19 :
Q. 23 The work function of a surface is 3.1 eV. A photon of frequency 1 × 1015 Hz. Is an, incident on it. Calculate the incident wavelength is photoelectric emission occurs or not., Ans.
Page 20 :
Q. 24 The primary of a transformer has 40 turns and works on 100 V and 100 W. Find a, number of turns in the secondary to step up the voltage to 400 V. Also calculate the current, in the secondary and primary., Ans.
Page 22 :
Q. 25 A circular loop of radius 9.7 cm carries a current 2.3 A. Obtain the magnitude of the, magnetic field, (a) at the centre of the loop, (b) at a distance of 9.7 cm from the centre of the loop but on the axis., Ans. A Data: R = z = 9.7 cm = 9.7 x 10-2 m, I = 2.3 A, N = l, (a) At the centre of the coil:, The magnitude of the magnetic induction,
Page 23 :
Ans. B Given:, R = 9.7 cm = 9.7 × 10-2 m,, I = 2.3 A,, z = 9.7 cm = 9.7 × 10-2 m, To find:
Page 24 :
Magnetic field, i., ii., , at the centre of the loop, on the axis at a distance, , Q. 26 A cell of e.m.f 1.5V and negligible internal resistance is connected in series with a, potential meter of length 10 m and the total resistance of 20 Ω. What resistance should be, introduced in the resistance box such that the potential drop across the potentiometer is, one microvolt per cm of the wire?, Ans. Given:
Page 25 :
R = 20 Ω, L = 10 m, E = 1.5 V,, K = 1 μV/cm = 1 × (10-6 /10-2 ) V/ m, = 10-4 V/ m, To find: External resistance (RE), , Q. 27 | Attempt Any Three:, Answer in brief: Explain the spectral distribution of blackbody radiation., Ans. 1 All objects with a temperature above absolute zero (0 K, -273.15oC) emit energy in, the form of electromagnetic radiation., A blackbody is a theoretical or model body that absorbs all radiation falling on it, reflecting, or transmitting none. It is a hypothetical object which is a “perfect” absorber and a, “perfect” emitter of radiation over all wavelengths.
Page 26 :
The spectral distribution of the thermal energy radiated by a blackbody (i.e. the pattern of, the intensity of the radiation over a range of wavelengths or frequencies) depends only on, its temperature., , The characteristics of blackbody radiation can be described in terms of several laws:, 1. Planck’s Law of blackbody radiation, a formula to determine the spectral energy, density of the emission at each wavelength (Eλ) at a particular absolute temperature, (T)., , 1. Wien’s Displacement Law, which states that the frequency of the peak of the, emission (fmax) increases linearly with absolute temperature (T). Conversely, as the, temperature of the body increases, the wavelength at the emission peak decreases., fmax α T, 2. Stefan–Boltzmann Law, which relates the total energy emitted (E) to the absolute, temperature (T)., E α T4, In the image above, notice that:, •, •, •, •, •, •, , The blackbody radiation curves have quite a complex shape (described by Planck’s, Law)., The spectral profile (or curve) at a specific temperature corresponds to a specific, peak wavelength, and vice versa., As the temperature of the blackbody increases, the peak wavelength decreases, (Wien’s Law)., The intensity (or flux) at all wavelengths increases as the temperature of the, blackbody increases., The total energy being radiated (the area under the curve) increases rapidly as the, temperature increases (Stefan–Boltzmann Law)., Although the intensity may be very low at very short or long wavelengths, at any, temperature above absolute zero energy is theoretically emitted at all wavelengths, (the blackbody radiation curves never reach zero).
Page 27 :
Ans. 2, i. The rate of emission per unit area or power per unit area of a surface is defined as a, function of the wavelength λ of the emitted radiation., ii. Scientists studied the energy distribution of blackbody radiation as a function of, wavelength., , iii., , By keeping the source of radiation (such as a cavity radiator) at different, temperatures they measured the radiant power corresponding to different, wavelengths. The measurements were represented graphically in the form of curves, showing the variation of radiant power per unit area as a function of wavelength λ, at different constant temperatures as shown in the figure., , Q. 28 State the postulates of Bohr’s atomic model. Hence show the energy of electrons, varies inversely to the square of the principal quantum number., Ans. Bohr’s three postulates are:, i., ii., , i., , In a hydrogen atom, the electron revolves around the nucleus in a fixed circular, orbit with constant speed., The radius of the orbit of an electron can only take certain fixed values such that the, angular momentum of the, , An electron can make a transition from one of its orbits to another orbit having, lower energy. In doing so, it emits a photon of energy equal to the difference in its, energies in the two orbits., , Expression for the energy of an electron in the nth orbit of Bohr’s hydrogen atom:, i., , Kinetic energy:, Let, me = mass of the electron, rn = radius of nth orbit of Bohr’s hydrogen atom, vn = velocity of electron
Page 28 :
−e = charge of the electron, +e = charge on the nucleus, Z = a number of electrons in an atom., According to Bohr’s first postulate,
Page 29 :
Q. 29. i Draw a neat labelled diagram showing energy levels and transition between them, for the hydrogen atoms., Ans. Energy levels and transition between them for hydrogen atom:
Page 30 :
Q. 29.ii An electron in an atom is revolving around the nucleus in a circular orbit of a, radius of 5.3 x 10-11 m, with a speed of 2 x 106 m/s. Find the resultant orbital magnetic, moment and angular momentum of the electron. [e = 1.6 x 10-19 C, me= 9.1 x 10-31 kg], Ans. A, i. Data: r = 5.3 × 10-11 m, v = 2 × 106 m/s,, e = 1.6 × 10-19 C, me = 9.1 × 10-31 kg, The orbital magnetic moment of the electron is
Page 31 :
Ans. B
Page 32 :
Q. 30.i Define magnetization. State its SI unit and dimensions. Derive the relation between, magnetic field intensity(H) and magnetization(M) for a magnetic material placed in a, magnetic field., Ans., i. The ratio of magnetic moment to the volume of the material is called magnetization., ii. Unit: Am-1 in SI system., iii. Dimensions: [M0 L-1 T0 I1], iv., Relation between magnetic field intensity(H) and magnetization(M):, a. Consider a magnetic material (rod) placed in a magnetizing field (solenoid with n, turns per unit length and carrying current I)., b. The magnetic field inside the solenoid is given by,, B0 = μ0nI ….(1)
Page 33 :
Where µ0 = permeability of free space., c. The magnetic field inside the rod is given as,, Bm = µ0M ….(2), Where M = magnetization of the material, d. The net magnetic field inside the rod is expressed as,, B = B0 + Bm ….(3), ∴ B = µ0nI + µ0M, ∴ B = µ0H + µ0M, e. Equation (4) shows that the magnetic field (B) induced in the material depends on, magnetic field intensity (H) and magnetization (M)., Q. 30.ii Two capacitors each of capacity 2 μF are connected in parallel. This system is, connected in series with the third capacitor of 12μF capacity. Find the equivalent capacity, of the system., Ans.
Page 34 :
Q. 31.i Using Ampere's law, obtain an expression for the magnetic induction near a, current-carrying straight infinitely long wire., Ans. Consider a long straight wire carrying a current I as shown in the figure below., , A long straight current-carrying wire, , Q. 31.ii Two spheres A and B of radius a and b respectively are at the same potential. Find, the ratio of the surface charge densities of A and B.