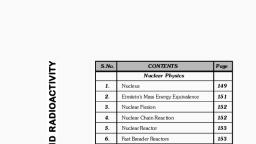
Page 1 :
Nuclei, Recap Notes, Composition of the Nucleus, X The nucleus of an atom contains protons, and neutrons which are collectively known, as nucleons. The number of protons in a, nucleus is called its atomic number and is, denoted by Z. The total number of protons, and neutrons in a nucleus is called its, mass number and is denoted by A., – Number of protons in an atom = Z, – Number of electrons in an atom = Z, – Number of nucleons in an atom = A, – Number of neutrons in an atom = N, = A – Z., X Nuclide : It is a specific nucleus of, an atom which is characterised by its, atomic number Z and mass number A., It is represented by ZXA where X is the, chemical symbol of the element., X Nuclear Radius : Nuclear radius R = R0, A1/3 where R0 is a constant and A is the, mass number., Nuclear radius is measured in fermi., 1 fm = 10–15 m, X Nuclear Density :, Mass of nucleus, Nuclear density, ρ =, Volume of nucleus, Nuclear density is independent of A and, is in order of the 1017 kg m–3., Isotopes : Isotopes of an element are the, atoms of the element which have the same, atomic number but different mass numbers,, e.g., 1H1, 1H2, 1H3, are the three isotopes of, hydrogen., Isobars : Isobars are the atoms of different, elements which have the same mass number, but different atomic numbers, e.g., 11Na 22, and 10Ne22., , Isotones : Isotones are the nuclides which, contain the same number of neutrons, e.g.,, 37, 39, 17Cl and 19K ., Nuclear forces : Nuclear forces are the, strong forces of attraction which hold, together the nucleons (neutrons and protons), in the tiny nucleus of an atom, inspite, of strong electrostatic forces of repulsion, between protons., X Nuclear forces are strongest forces in, nature., X Nuclear forces are short range forces., X Nuclear forces do not obey inverse square law., X Nuclear forces are charge independent., Mass defect : The difference in mass of a, nucleus and its constituents is known as the, mass defect and is given by, Dm = [Zmp + (A – Z)mn – mN], where mp is the mass of the proton and mn is, the mass of the neutron and mN is the mass, of the nucleus., Binding Energy : The binding energy of, nucleus is given by, Eb = Dmc2 = [Zmp + (A – Z)mn – mN]c2, = [Zmp + (A – Z)mn – mN] × 931.49 MeV/u., Nuclear reaction : A nuclear reaction is, represented by, A+a→B+b+Q, where A is the target nucleus, a is the, impinging particle, B and b are the products,, Q is the energy released in the process., The nuclear reaction is represented by, notation A(a, b)B., Q value of nuclear reaction,, Q = (mA + ma – mB – mb)c2

Page 2 :
X, , X, , X, , If Q is positive, the reaction is exothermic, and if Q is negative the reaction is, endothermic., Conservation laws obeyed by every, nuclear reaction are, – Conservation of charge number, – Conservation of mass number, – Conservation of linear momentum, – Conservation of energy, Nuclear fission : It is the phenomenon of, splitting a heavy nucleus into two or more, smaller nuclei., The nuclear fission of 92U235 is represented, as, 235, , 92U, , + 0n1 → 56Ba141 + 36Kr92 + 3 0n1 + Q, , The value of the Q is 200 MeV per fission, reaction., X Nuclear chain reaction : Under suitable, conditions, the three secondary neutrons, may cause further fission of U235 nuclei, and start what is known as nuclear chain, reaction. The nuclear chain reaction is, controlled by, Neutron reproduction factor, (K), Rate of production of neutrons, =, Rate of loss of neutrons, , X, , X, , X, , X, , Uncontrolled nuclear chain reaction is the, basis of an atom bomb. Controlled nuclear, chain reaction is the basis of a nuclear, reactor., Nuclear reactor : Nuclear reactor uses, nuclear energy for peaceful purposes. It, is based on the phenomenon of controlled, nuclear chain reaction. Moderators like, heavy water, graphite, paraffin and, deuterium slow down neutrons. Rods of, cadmium and boron serve as control rods., Ordinary water and heavy water serve as, coolants., Nuclear fusion : It is the phenomenon of, fusing two or more lighter nuclei to form a, single heavy nucleus., – The nuclear fusion reaction of two, deutrons is represented as, – 1H2 + 1H2 → 2He4 + 24 MeV, – Temperature ≈ 107 K are required for, fusion to take place., – Nuclear fusion is a basis of hydrogen, bomb., Stellar energy : It is the energy obtained, from the sun and stars. The source of, stellar energy is nuclear fusion.

Page 3 :
Practice Time, OBJECTIVE TYPE QUESTIONS, , Multiple Choice Questions (MCQs), 1. If 200 MeV energy is released in the fission, of a single nucleus of 235, 92U, the fissions which are, required to produce a power of 1 kW is, (a) 3.125 × 1013, (b) 1.52 × 106, 12, (c) 3.125 × 10, (d) 3.125 × 1014, The equation 4 11 H +, , 4, 2+, 2 He, , 2., →, represents, (a) both fusion and fission, (b) neither fusion nor fission, (c) only fusion, (d) only fission, 3., (a), (b), (c), (d), , −, , + 2e + 26 MeV, , In nuclear reaction, there is conservation of, mass only, energy only, momentum only, mass, energy and momentum, , 4. The fission properties of 239, 94 Pu are very, similar to those of 235, U., The, average energy, 92, released per fission is 180 MeV. If all the atoms, in 1 kg of pure 239, 94Pu undergo fission, then the, total energy released in MeV is, (a) 4.53 × 1026 MeV, (b) 2.21 × 1014 MeV, 13, (c) 1 × 10 MeV, (d) 6.33 × 1024 MeV, 5. 1 MeV positron encounters a 1 MeV, electron travelling in opposite direction., What is the wavelength of photons produced?, (Given rest mass energy of electron or positron, = 0.512 MeV and h = 6.62 × 10–34 Js), (a) 8.2 × 10–11 m, (b) 8.2 × 10–13 m, –12, (c) 8.2 × 10, m, (d) 8.2 × 10–9 m, , 8. The mass number of iron nucleus is 55.854, and A = 56, the nuclear density is, (a) 2.29 × 1016 kg m–3 (b) 2.29 × 1017 kg m–3, (c) 2.29 × 1018 kg m–3 (d) 2.29 × 1015 kg m–3, 9. Order of magnitude of density of uranium, nucleus is, (a) 1020 kg m–3, (b) 1017 kg m–3, 14, –3, (c) 10 kg m, (d) 1011 kgm–3, 10. How much mass has to be converted into, energy to produce electric power of 500 MW for, one hour?, (a) 2 × 10–5 kg, (b) 1 × 10–5 kg, (c) 3 × 10–5 kg, (d) 4 × 10–5 kg, 11. Two stable isotopes 36 Li and 37 Li have, respective abundances of 7.5% and 92.5%. These, isotopes have masses 6.01512 u and 7.01600 u, respectively. The atomic weight of lithium is, (a) 6.941 u, (b) 3.321 u, (c) 2.561 u, (d) 0.621 u, 12. The ratio of the nuclear radii of the gold, 197, isotope 79 Au and silver isotope 107, 47Ag is, (a) 1.23, (b) 0.216, (c) 2.13, (d) 3.46, 13. Let mp be the mass of a proton, mn the mass, 20, of a neutron, M1 the mass of a 10, Ne nucleus and, 40, M2 the mass of a 20 Ca nucleus. Then, (a) M2 = M1, (b) M2 > 2M1, (c) M2 = 2M1, (d) M1 < 10 (mn + mp), Light energy emitted by star is due to, breaking of nuclei, joining of nuclei, burning of nuclei, reflection of solar light, , 6. In nuclear reactors, the control rods are, made of, (a) cadmium, (b) graphite, (c) krypton, (d) plutonium, , 14., (a), (b), (c), (d), , 7. The equivalent energy of 1 g of substance is, (a) 9 × 1013 J, (b) 6 × 1012 J, 13, (c) 3 × 10 J, (d) 6 × 1013 J, , 15. The mass of proton is 1.0073 u and that of, neutron is 1.0087 u (u = atomic mass unit). The, 4, binding energy of 24 He, if mass of 2He is 4.0015 u

Page 4 :
(a) 0.0305 erg, (c) 28.4 MeV, , (b) 0.0305 J, (d) 0.061 u, , 16. The set which represents the isotope, isobar, and isotone respectively is, 198, 3, 2, (a) (12H, 13H), (197, 79Au, 80Hg) and (2 He, 1 H), , (b), , 198, (23He, 11H), (197, 79Au, 80Hg), , and, , (11H, 31H), , 198, (c) (23He, 13H), (12H, 13H) and (197, 79Au, 80Hg), 198, (d) (12H, 13H), (23He, 13H) and (197, 79Au, 80Hg), , 17. The radius of a spherical nucleus as measured, by electron scattering is 3.6 fm. What is the mass, number of the nucleus most likely to be?, (a) 27, (b) 40, (c) 56, (d) 120, , 18. If in a nuclear fusion reaction, mass defect is, 0.3%, then energy released in fusion of 1 kg mass, is, (a) 27 × 1010 J, (b) 27 × 1011 J, 10, (c) 27 × 10 J, (d) 27 × 1013 J, 19. If the nucleus 13Al27 has a nuclear radius of, about 3.6 fm, then 52Te125 would have its radius, approximately as, (a) 9.6 fm, (b) 12 fm, (c) 4.8 fm, (d) 6 fm, 20. Boron has two stable isotopes, 105B and 115B., Their respective masses are 10.01294 u and, 11.00931 u, and the atomic mass of boron is, 10.811 u. Find the abundances of 115B., (a) 90.1%, (b) 80.1%, (c) 85.5%, (d) 95%, , Case Based MCQs, Case I : Read the passage given below and answer, the following questions from 21 to 25., Discovery of Nucleus, The nucleus was first discovered in 1911 by Lord, Rutherford and his associates by experiments, on scattering of a-particles by atoms. He found, that the scattering results could be explained,, if atoms consist of a small, central, massive and, positive core surrounded by orbiting electrons., The experimental results indicated that the size, of the nucleus is of the order of 10–14 m and is, thus 10000 times smaller than the size of atom., 21. Ratio of mass of nucleus with mass of atom is, approximately, (a) 1, (b) 10, 3, (c) 10, (d) 1010, 22. Masses of nuclei of hydrogen, deuterium and, tritium are in ratio, (a) 1 : 2 : 3, (b) 1 : 1 : 1, (c) 1 : 1 : 2, (d) 1 : 2 : 4, 23. Nuclides with same neutron number but, different atomic number are, (a) isobars, (b) isotopes, (c) isotones, (d) none of these, 24. If R is the radius and A is the mass number,, then log R versus log A graph will be, (a) a straight line, (b) a parabola, (c) an ellipse, (d) none of these., , 25. The ratio of the nuclear radii of the mercury, 107, isotope 198, 80Hg and silver isotope 47Ag is, (a) 1.23, (b) 0.216, (c) 2.13, (d) 3.46, Case II : Read the passage given below and, answer the following questions from 26 to 30., Nuclear Fission, In the year 1939, German scientist Otto Hahn, and Strassmann discovered that when an, uranium isotope was bombarded with a neutron,, it breaks into two intermediate mass fragments., It was observed that, the sum of the masses of, new fragments formed were less than the mass, of the original nuclei. This difference in the mass, appeared as the energy released in the process., Thus, the phenomenon of splitting of a heavy, nucleus (usually A > 230) into two or more lighter, nuclei by the bombardment of proton, neutron,, a-particle, etc with liberation of energy is called, nuclear fission., 235, 236, + 0n1 →, → 56Ba144 + 36Kr89, 92U, 92U, , , 26., of, (a), (b), (c), (d), , Unstable nucleus, , + 30n1 + Q, , Nuclear fission can be explained on the basis, Millikan’s oil drop method, Liquid drop model, Shell model, Bohr’s model.

Page 5 :
27. For sustaining the nuclear fission chain, reaction in a sample (of small size) of 235, 92U, it is, desirable to slow down fast neutrons by, (a) friction, (b) elastic damping/scattering, (c) absorption, (d) cooling, , (a) more mass per nucleon than either of the two, fragments, (b) more mass per nucleon as the two fragment, (c) exactly the same mass per nucleon as the, two fragments, (d) less mass per nucleon than either of two, fragments., , 28. Which of, reaction(s)?, , 33. When 92U235 undergoes fission, about 0.1%, of the original mass is converted into energy. The, energy released when 1 kg of 92U235 undergoes, fission is, , (I), , 1, 0n, , the, , following, , is/are, , fission, , 236, 133, 99, 1, + 235, 92U → 92U → 51Sb + 41Nb + 4 0n, , 1.40, 94, 1, (II) 10n + 235, 92U → 54 Xe + 38Sr + 2 0n, , (III) 21H + 21H → 32He + 10n, (a) Both II and III, (c) Only II, , (b) Both I and III, (d) Both I and II, , 29. On an average, the number of neutrons and, the energy of a neutron released per fission of a, uranium atom are respectively, (a) 2.5 and 2 keV, (b) 3 and 1 keV, (c) 2.5 and 2 MeV, (d) 2 and 2 keV, 30. In any fission process, ratio of mass of, daughter nucleus to mass of parent nucleus is, (a) less than 1, (b) greater than 1, (c) equal to 1, (d) depends on the mass of parent nucleus., Case III : Read the passage given below and, answer the following questions from 31 to 35., Nuclear Energy, A heavy nucleus breaks into comparatively, lighter nuclei which are more stable compared to, the original heavy nucleus. When a heavy nucleus, like uranium is bombarded by slow moving, neutrons, it splits into two parts releasing large, amount of energy. The typical fission reaction of, 235, ., 92U, 235, 92U, , + 0n1 → 56Ba141 + 36Kr92 + 30n1 + 200 MeV, , The fission of 92U235 approximately released, 200 MeV of energy., 31. If 200 MeV energy is released in the fission, of a single nucleus of 235, 92U, the fissions which are, required to produce a power of 10 kW is, (a) 3.125 × 1013, (b) 1.52 × 106, 12, (c) 3.125 × 10, (d) 3.125 × 1014, 32. The release in energy in nuclear fission is, consistent with the fact that uranium has, , (a) 9 × 1011 J, (c) 9 × 1015 J, , (b) 9 × 1013 J, (d) 9 × 1018 J, , 34. A nuclear fission is said to be critical when, multiplication factor or K, (a) K = 1, (b) K > 1, (c) K < 1, (d) K = 0, 35. Einstein’s mass-energy conversion relation, E = mc2 is illustrated by, (a) nuclear fission, (b) atomic transition, (c) rocket propulsion, (d) steam engine, Case IV : Read the passage given below and, answer the following questions from 36 to 40., Nuclear Force, Neutrons and protons are identical particle in, the sense that their masses are nearly the same, and the force, called nuclear force, does into, distinguish them. Nuclear force is the strongest, force. Stability of nucleus is determined by the, neutron proton ratio or mass defect or packing, fraction. Shape of nucleus is calculated by, quadrupole moment and spin of nucleus depends, on even or odd mass number. Volume of nucleus, depends on the mass number. Whole mass of the, atom (nearly 99%) is centred at the nucleus., 36. The correct statements about the nuclear, force is/are, (a) charge independent, (b) short range force, (c) non-conservative force, (d) all of these., 37. The range of nuclear force is the order of, (a) 2 × 10–10 m, (b) 1.5 × 10–20 m, (c) 1.2 × 10–4 m, (d) 1.4 × 10–15 m, 38. A force between two protons is same as the, force between proton and neutron. The nature of, the force is

Page 6 :
(a) electrical force, (c) gravitational force, , (b) weak nuclear force, (d) strong nuclear force., , 39. Two protons are kept at a separation of 40 Å., Fn is the nuclear force and Fe is the electrostatic, force between them. Then, (a) Fn << Fe, (b) Fn = Fe, , (c) Fn >> Fe, 40., (a), (b), (c), (d), , (d) Fn ≈ Fe, , All the nucleons in an atom are held by, nuclear forces, Van der Waal’s forces, tensor forces, coulomb forces, , Assertion & Reasoning Based MCQs, For question numbers 41-49, two statements are given-one labelled Assertion (A) and the other labelled Reason (R)., Select the correct answer to these questions from the codes (a), (b), (c) and (d) as given below., (a) Both A and R are true and R is the correct explanation of A, (b) Both A and R are true but R is NOT the correct explanation of A, (c) A is true but R is false, (d) A is false and R is also false, 41. Assertion (A) : Two protons can attract, each other., Reason (R) : The distance between the protons, within the nucleus is about 10–15 m., , 46. Assertion (A) : There is a chain reaction, when uranium is bombarded with slow neutrons., Reason (R) : When uranium is bombarded with, slow neutrons more neutrons are produced., , 42. Assertion (A) : The nuclear force becomes, weak if the nucleus contains too many protons, compared to neutrons., Reason (R) : The electrostatic forces weaken the, nuclear force., , 47. Assertion (A) : Cadmium rods used in a, nuclear reactor, control the rate of fission., Reason (R) : Cadmium rods speed up the slow, neutrons., , 43. Assertion (A) : For the fission of heavy, nuclei, neutrons are more effective than protons., Reason (R) : Neutrons are heavier than protons., 44. Assertion (A) : Energy is released in a, nuclear reaction., Reason (R) : In any nuclear reaction the, reactants and resultant products obey the law of, conservation of charge and mass only., 45. Assertion (A) : Density of all the nuclei is same., Reason (R) : Radius of nucleus is directly, proportional to the cube root of mass number., , 48. Assertion (A) : A fission reaction can be, more easily controlled than a fusion reaction., Reason (R) : The percentage of mass converted, to energy in a fission reaction is 0.1% whereas, in a fusion reaction it is 0.4%., 49. Assertion (A) : Thermonuclear fusion, reactions may become the source of unlimited, power for the mankind., Reason (R) : A single fusion event involving, isotopes of hydrogen produces more energy than, energy from nuclear fission of a single uranium., , SUBJECTIVE TYPE QUESTIONS, , Very Short Answer Type Questions (VSA), 1., , What is the radius of the nucleus of, , 2., , Find, , 64, 29 Cu, , the, , 27, and 13, Al ., , ratio, , of, , nuclear, , 3., , 64, 29 Cu?, , radius, , of, , Define the nuclear force?, , 4. The nuclear radius of a nucleus with nucleon, number 16 is 3 × 10–15 m. Then, find the nuclear, radius of a nucleus with nucleon number 128?

Page 7 :
5. Assume that a neutron breaks into a proton, and an electron. Find the energy required during, this process ?, (Mass of neutron = 1.6725 × 10–27 kg, Mass of proton, = 1.6725 × 10–27 kg, mass of electron = 9 × 10–31 kg), 6. A neutron is absorbed by a 63 Li nucleus with, the subsequent emission of an alpha particle., Calculate the energy released, in MeV, in this, reaction., [Given : mass, , 6, 3 Li, , and mass (triton) = 3.0100000 u., Take 1 u = 931 MeV/c2], 7. From the relation R = R0 A1/3, where R0 is a, constant and A is the mass number of a nucleus,, show that the nuclear matter density is nearly, constant (i.e., independent of A)., 8., , The three stable isotopes of neon :, , 21, 10 Ne, , and, , 22, 10 Ne, , 20, 10 Ne, , ,, , have respective abundances of, , 90.51%, 0.27% and 9.22%. The atomic masses, of the three isotopes are 19.99 u, 20.99 u and, 21.99 u, respectively. Obtain the average atomic, mass of neon., , = 6.015126 u;, , mass (neutron) = 1.0086654 u;, mass (alpha particle) = 4.0026044 u;, , Short Answer Type Questions (SA-I), 9. Find the disintegration energy Q for the, fission event represented by equation, 235, 94, 1, + 0n1 → 92U236 → 140, 92U, 58Ce + 40Zr + 20n, If mass of 92U235 = 235.0439 u, 0n1 = 1.00867 u,, 140, 94, 58Ce = 139.9054 u and 40Zr = 93.9063 u, find, energy released in the process., 10. 92U235 absorbs a slow neutron (thermal, neutron) and undergoes a fission represented by, 235, + 0n1 → 92U236 → 56Ba141 + 36Kr92 + 3 0n1 + E., 92U, , Calculate :, (i) The energy released E per fission., (ii) The energy released when 1 g of, undergoes complete fission., Given : 92U235 = 235.1175 amu (atom),, , 235, 92U, , is mass converted into energy (or vice versa)?, Explain giving one example., 12. Calculate the energy released in fusion, reaction : 12 H +12 H → 32 He + n , where B.E. of, 2, 1H, , = 2.23 MeV and of, , 3, 2 He, , = 7.73 MeV., , 13. Which is more, the density of lead nuclei or, the density of oxygen nuclei?, 14. Consider a particle or, nucleus, which, contains 2 protons and 2 neutrons. Find its, binding energy., mp = 1.007276 u, mn = 1.008665 u, mHe = 4.001508 u, , 1 amu = 931 MeV/c, , 15. A nuclide 1 is said to be the mirror isobar of, nuclide 2 if Z1 = N2 and Z2 = N1. (a) Which nuclide, is a mirror isobar of 23, 11Na ? (b) Which nuclide out, of the two mirror isobars have greater binding, energy and why?, , 11. If both the number of protons and neutrons, in a nuclear reaction is conserved, in what way, , 16. Why do stable nuclei never have more, protons than neutrons?, , 141, = 140.9577 amu (atom), 56Ba, 92, 1, 36Kr = 91.9264 amu (atom), 0n =, 2, , 1.00868 amu,, , Short Answer Type Questions (SA-II), 17. Calculate for how many years will the fusion, of 2.0 kg deuterium keep 800 W electric lamp, glowing. Take the fusion reaction as, 2, 2, 3, 1, 1H + 1H → 2He + 0n + 3.27 MeV, 18. Consider the fusion reaction:, 4, He + 4He → 8Be, For the reaction, find (i) mass defect (ii) Q-value, (iii) Is such a fusion energetically favourable?, , Atomic mass of 8Be is 8.0053 u and that of 4He, is 4.0026 u., 19. A nuclear reactor using 235U generates 250 MW, of electrical power. The efficiency of the reactor, (i.e., efficiency of conversion of thermal energy, into electrical energy) is 25%. What is the amount, of 235U used in the reactor per year? The thermal, energy released per fission of 235U is 200 MeV.

Page 8 :
20. The deuteron is bound by nuclear forces, just as H-atom is made up of p and e bound by, electrostatic forces. If we consider the force, between neutron and proton in deuteron as given, in the form of a Coulomb potential but with an, effective charge e′:, 1 e′ 2, F=, 4 πε0 r, , 22. When four hydrogen nuclei combine to form, a helium nucleus estimate the amount of, energy in MeV released in this process of fusion, (Neglect the masses of electrons and neutrons)., Given:, , Estimate the value of (e′/e) given that the binding, energy of a deuteron is 2.2 MeV., , 23. In a typical nuclear reaction, e.g., , 21. Distinguish between the phenomena of, nuclear fission and fusion., , although number of nucleons is conserved, yet, energy is released. How? Explain., , (i) Mass of 11 H = 1.007825 u, (ii) mass of helium nucleus = 4.002603 u,, , 1u = 931 MeV/c2, 2, 1H, , + 12 H →32 He + 10 n +3.27 MeV,, , Long Answer Type Questions (LA), 24. Deuteron is a bound state of a neutron and a, proton with a binding energy B = 2.2 MeV. A g-ray, of energy E is aimed at a deuteron nucleus to try, to break it into a (neutron + proton) such that, , the n and p move in the direction of the incident, g-ray. If E = B, show that this cannot happen., Hence, calculate how much E should be bigger, than B for such a process to happen., , OBJECTIVE TYPE QUESTIONS, , 6. (a) : In nuclear reactors, cadmium rods are used as, control rods., 7. (a) : Using, E = mc2, Here, m = 1 g = 1 × 10–3 kg,, c = 3 × 108 m s–1, \ E = 10–3 × 9 × 1016 = 9 × 1013 J, 8. (b), 9. (b) : Order of magnitude of nuclear density = 1017 kg m–3, 10. (a) : Here, P = 500 MW = 5 × 108 W, t = 1 h = 3600 s, Energy produced, E = P × t = 5 × 108 × 3600 = 18 × 1011 J, As E = mc2, , 1. (a) : Let the number of fissions per second be n., Energy released = n × 200 MeV = n × 200 × 1.6 × 10–13 J, Energy required = power × time = 1 kW × 1 s = 1000 J, \ n × 200 × 1.6 × 10–13 = 1000, 1000, 10, or n =, =, × 1013 = 3.125 × 1013, −11 3.2, 3.2 × 10, 2. (c) : During nuclear fusion, two or more lighter nuclei, combine to form a heavier nucleus., 3. (d) : In any nuclear reaction mass, energy and momentum, all are conserved., 4. (a) : Number of atoms in 1 kg of pure 239Pu, 23, , 6.023 × 10, × 1000 = 2.52 × 1024, 239, As average energy released per fission is 180 MeV, \ Total energy released = 2.52 × 1024 × 180 MeV, , = 4.53 × 1026 MeV, 0, 0, 5. (b) : –1 e + +1 e → 2g, The total energy of the positron = 1 + 0.512 MeV, The total energy of the electron = 1 + 0.512 MeV, Energy of each photon, 2(1+ 0.512), =, = 1.512 MeV = 1.512 × 1.6 × 10 −13 J, 2, hc, hc 6.62 × 10 −34 × 3 × 108, E=, ⇒λ=, =, λ, E, 1.512 × 1.6 × 10 −13, –13, = 8.2 × 10 m, =, , \, , E, 18 × 1011 18 × 1011, = 2 × 10 −5 kg, =, m= 2=, c, (3 × 108 )2 9 × 1016, , 11. (a) : Atomic weight = Weighted average of the isotopes, 6.01512 × 7.5 + 7.01600 × 92.5, =, (7.5 + 92.5), 45.1134 + 648.98, =, = 6.941 u, 100, 12. (a) : Here, A1 = 197 and A2 = 107, 1/ 3, , \, , R1  A1 , = , R2  A2 , , 1/ 3, ,  197 , =, ,  107 , , = 1.225  1.23, , 13. (d) : Due to mass defect, the rest mass of a nucleus is, always less than the sum of the rest masses of its constituent, nucleons.

Page 9 :
20, 10Ne, , nucleus consists of 10 protons and 10 neutrons., \ M1 < 10 (mp + mn), 14. (b) : Light energy emitted by stars is due to fusion of light, nuclei., 15. (c) : Dm = 2mp + 2mn – m(42He), = 2 × 1.0073 + 2 × 1.0087 – 4.0015 = 0.0305 u, Binding energy = 0.0305 × 931 MeV = 28.4 MeV, 16. (d) : Nuclides with same atomic number Z but different, mass number A are known as isotopes., Nuclides with same mass number A but different atomic, number Z are known as isobars., Nuclides with same neutron number N = (A – Z ) but different, atomic number Z are known as isotones., 2, 3, 1H and 1H are isotopes, 3, 3, 2He and 1H are isobars, 197, and 80Hg198 are isotones., 79Au, 17. (a) : Nuclear radius, R = R0(A)1/3, where A is the mass number of a nucleus., Given, R = 3.6 fm, ∴ 3.6 fm = (1.2 fm)( A1/ 3 ), or, , [∵R0 = 1.2 fm], , A = (3)3 = 27, , 0 .3, kg = 3 × 10 −3 kg, 100, \ E = (Dm) c2 = 3 × 10–3 × (3 × 108)2 = 27 × 1013 J, 19. (d) : Here, A1 = 27, A2 = 125, R1 = 3.6 fm, 18. (d) : Here, Dm = 0.3% of 1 kg =, , 1/ 3, , 1/ 3, R2  A2 , 5,  125 , =  =, =,  27 , 3, R1  A1 , \ R = 5 R = 5 × 3.6 = 6 fm, 2, 3 1 3, 20. (b) : Let abundance of 105B is x % than abundance of 115B, will be (100 – x)%., Atomic mass of boron, x [10.01294 u] + (100 − x )[11.00931u], =, 100, ⇒ 100 × 10811 u = 1100.931 u – 0.99637x u, 19.831, Solving we get, x =, = 19.9%, 0.99637, , As,, , So, relative abundance of 105B isotope = 19.9%, Relative abundance of 115B isotope = 80.1%, 21. (a) : As nearly 99.9% mass of atom is in nucleus, Mass of nucleus 99.9, ∴, =, = 0.99 ≈ 1, Mass of atom, 100, 22. (a) : Since, the nuclei of deuterium and tritium are, isotopes of hydrogen, they must contain only one proton each., But the masses of the nuclei of hydrogen, deuterium and, , tritium are in the ratio of 1 : 2 : 3, because of presence of, neutral matter in deuterium and tritium nuclei., 23. (c), 24. (a) : R = R0A1/3, 1, log R = log R0 +, log A, 3, Which is of form, y = mx + c. So, the graph between log A and, log R is a straight line., 25. (a) : Here, A1 = 198 and A2 = 107, 1/ 3, , 1/ 3, , R1  A1 ,  198 , =  =,  = 1.23, R2  A2 ,  107 , 26. (b), 27. (b) : Fast neutrons are slowed down by elastic scattering, with light nuclei as each collision takes away nearly 50% of, energy., 28. (d) : Reactions I and II represent fission of uranium, isotope 235, 92U, when bombarded with neutrons that breaks, it into two intermediate mass nuclear fragments. However,, reaction III represents two deuterons fuses together to from, the light isotope of helium., 29. (c) : On an average 2.5 neutrons are released per fission, of the uranium atom., The energy of the neutron released per fission of the uranium, atom is 2 MeV., 30. (a) : In fission process, when a parent nucleus breaks, into daughter products, then some mass is lost in the form of, energy. Thus,, mass of fission products < mass of parent nucleus., Mass of fission products, ⇒, <1, Mass of parent nucleus, \, , 31. (d) : Let the number of fissions per second be n., Energy released = n × 200 MeV = n × 200 × 1.6 × 10–13 J, Energy required = power × time = 10 kW × 1 s = 10000 J, \ n × 200 × 1.6 × 10–13 = 10000, 10000, or n =, = 3.125 × 1014, −11, 3.2 × 10, 32. (a), 33. (b) : As only 0.1% of the original mass is converted into, energy, hence out of 1 kg mass 1 g is converted into energy., \ Energy released during fission, E = Dmc2, = 1 g × (3 × 108 m s–1)2 = 10–3 × 9 × 1016 J = 9 × 1013 J, 34. (a) , 35. (a), 36. (d) : All options are basic properties of nuclear forces. So,, all options are correct., 37. (d) : The nuclear force is of short range and the range of, nuclear force is the order of 1.4 × 10–15 m., Now, volume ∝ R3 ∝ A

Page 10 :
38. (d), 39. (a) : Nuclear force is much stronger than the electrostatic, force inside the nucleus i.e., at distances of the order of fermi., At 40 Å, nuclear force is ineffective and only electrostatic, force of repulsion is present. This is very high at this distance, because nuclear force is not acting now and the gravitational, force is very feeble. Fnuclear << Felectrostatic in this case., 40. (a), 41. (a) : Due to electrostatic forces between two protons, (like charges) there is a force of repulsion. However, when, the distance between them is ~ 10–15 m they come under, the influence of the short range, strong nuclear forces. (The, range of the nuclear forces is ~ 10–15 m). These forces are, attractive forces and charge independent. The net force on the, protons is attractive as nuclear forces are much stronger than, electrostatic forces. The protons attract each other., 42. (c) : Nuclear forces are strongest when the number of, protons equals the number of neutrons. An excess of protons, compared to neutrons weakens the nuclear force. Also too, many neutrons compared to protons inside the nucleus, weaken the nuclear forces. The electrostatic force which is a, hundred times less than the nuclear force is not the cause., 43. (b) : A neutron is slightly heavier than a proton. As, neutrons are chargeless particles they penetrate matter more, than protons. Therefore, they are more effective than protons, in fission reactions., 44. (c) : In both fission and fusion large amount of energy is, released. Assertion is correct. Charge, mass, momentum and, energy, all are conserved., 45. (a) : Experimentally, it is found that the average radius of, a nucleus is given by, R = R0A1/3 where R0 = 1.1 × 10–15 m = 1.1 fm, and A = mass number, 4, 4, The volume of a nucleus is V = p R3 = p R03A., 3, 3, Now as the masses of a proton and a neutron are roughly, equal, say m, the mass of a nucleus is also roughly proportional, to the mass number A, M = mA. Hence density within a, M, mA, m, nucleus, ρ = =, is independent of the, =, 4 3, 4 3, V, πR, πR A, 3 0, 3 0, mass number A., 46. (a) : When uranium is bombarded by slow neutrons the, reaction is represented as, 235, 1, 92 U + 0n, , 92, 1, → 141, 56 Ba + 36Kr + 30n + Energy., As more neutrons are produced, the reason is correct. These, additional neutrons strike other uranium nuclei to produce, even more neutrons. Thus a chain reaction is established., 47. (c) : Cadmium rods are used in a nuclear reactor to, control the rate of fission. The cadmium rods do not slow, down or speed up the neutrons produced in a fission reaction, of 235U. Instead they absorb the neutrons thereby regulating, , the power level of the reactor., 48. (b) : Percentage of mass converted to energy in a fission, reaction is 0.1% whereas in a fusion reaction it is 0.4%., Consequently the amount of energy released is more in a, fusion than in a fission reaction., It is not easy to control a fusion reaction., 49. (c) : When fusion is achieved by raising the temperature, of the system so that particles have enough kinetic energy, to overcome the coulomb repulsive behaviour, it is called, thermonuclear fusion. It is clean source of energy but energy, released in one fusion is much less than a single uranium, fission., , SUBJECTIVE TYPE QUESTIONS, 1., , 2., , As, R = R0A1/3 = (1.2 × 10–15)(64)1/3 = 4.8 × 10–15 m, ( R0 = 1.2 × 10–15 m), As, R = R0, , 1, 3, A, 1, , 1, , RCu  Acu  3  64  3 4, ⇒, =,  =  =, R Al  AAl , 3,  27 , 3. Nuclear force is the strongest attractive force which binds, the protons and neutrons together inside a tiny nucleus., 4. Radius R of a nucleus changes with the nucleon number, A of the nucleus as, R, A , Hence, 2 =  2 , R1  A1 , \, , 1/ 3, ,  128 , =,  16 , , 1/ 3, , = (8)1/3 = 2, , R2 = 2R1 = 2(3 × 10–15)m = 6 × 10–15 m, , 5. 0n1 → 1H1 + –1e0 + ν + Q, Dm = mn – ma – me, = (1.6725 × 10–27 – 1.6725 × 10–27 – 9 × 10–31) kg = – 9 × 10–31 kg, Energy = Dmc2 = 9 × 10–31 × (3 × 108)2 = 0.511 MeV, 6. 3Li6 + 0n1 → 2He4 + 1H3 + Q, Total initial mass = 6.015126 + 1.0086654 = 7.0237914 amu, Total final mass = 4.0026044 + 3.01 = 7.0126044 amu, Mass defect, Dm = 7.0237914 – 7.0126044 = 0.0111870 amu, Energy released, Q = 0.0111870 × 931 = 10.415 MeV., 7., , Density of nuclear matter =, , Mass of nucleus, Volume, , A × 1 amu, , where R = R0 A1/ 3 ( R0 = 1.2 × 10–15 m), 4, 3, πR, 3, A × 1 amu 1 amu 3 amu, =, =, Density, ρ =, 3, 4, 4, πR03A, πR03 4 πR0, 3, 3, 3 × 1.66 × 10 −27, =, 4 × 3.14 × (1.2 × 10 −15 )3, ρ=, , , , = 2.27 × 1017 kg m–3

Page 11 :
As R0 is constant, r is constant, So, nuclear density is constant irrespective of mass number or size., 8. , Average atomic mass of neon with the given abundances,, 90.51 (19.99 u) + 0.27 (20.99 u) + 9.22 (21.99 u), A=, 100, 2017.7, A=, u = 20.18 u, 100, , 14. , B.E. = (2mp + 2mn – mHe)u × 931 MeV, = [2(1.007276 u + 1.008665 u) – 4.001508 u] × 931 MeV, = [4.031882 u – 4.001508 u] × 931 MeV, = 0.030374 × 931 MeV, B.E. = 28.3 MeV, , 9. , The mass lost in the process,, Dm = 235.0439 + 1.00867 – (139.9054 + 93.9063 + 2.01734), = 0.22353 u, The corresponding energy released, = Dmc2 = 0.22353 × 931 MeV = 208 MeV, 10. , (i) E = [MU + mn – MBa – MKr – 3mn] × 931 = 200.57 MeV, NA, ×E, (ii) Energy released =, 235, 200.57 × 106 × 1.6 × 10−19 × 6.023 × 1023, =, = 22.84 MWh, 235 × 3.6 × 106, 11. , A certain number of neutrons and protons are brought, together to form a nucleus of a certain charge and mass, an, energy DEb will be released in this process., The energy DEb is called the binding energy of the nucleus., If we separate a nucleus into its nucleons we would have to, transfer a total energy equal to DEb, to the nucleons., , 23, For mirror isobar of 11, Na, Z 2 = N1 = 12 and N2 = Z1 = 11., , 92, 1, Example : 92 U235 + 0 n1 → 141, 56 Ba + 36Kr + 30 n + Q, The energy (Q) released was estimated to be 200 MeV per, fission and is equivalent to the difference in masses of the, nuclei before and after the fission., 12. Given fusion reaction,, , Energy released = final B.E. – initial B.E., = 7.73 – (2.23 + 2.23) = 3.27 MeV., 13. , We know that the density of solid lead is much greater, than the density of gaseous oxygen. But here we are checking, about the densities of their nuclei., If the mass of a neutron is m, then mass of nuclei, M = Am., 4, Now, volume V = pR3, 3, 4, But R = R0A1/3 or V = p(R0A1/3)3, 3, 4, V = pR03A, 3, M, The density of the nucleus r =, V, Am, 3m, =, =, = constant., 3, 4 3, πR0 A 4 πR0, 3, Nuclear density is almost a constant, whether it is lead or, oxygen., , 23, , 15. (a) For 11 Na , Z1 = 11, N1 = 12, 23, 23, Thus mirror isobar of 11, Na is 12, Mg ., 23, (b) As 12, Mg contains even number of protons (12) against, 23, 11 Na, , which contains odd number of protons (11), hence, , 23, 12 Mg, , has greater binding energy comparatively., 16. , The stability of a nucleus depends on its neutron to proton, ratio. More is the number of protons in the nucleus, greater is, the electrical forces between them. Therefore more neutrons, are needed to provide the strong attractive force necessary to, keep the nucleus stable., 17. , Given m = 2 kg, P = 800 W., Here two deuterium nuclei produce 3.27 MeV energy, , = 3.27 × 106 × 1.6 × 10–19 = 5.232 × 10–13 J, 5.232 × 10 −13, = 2.616 × 10–13 J, 2, No. of deuterium atom in 2 kg, \ Energy per nuclei =, , 6.023 × 1023 × 2000, = 6.023 × 1026 atom, 2, \ Total energy = 6.023 × 1026 × 2.616 × 10–13, = 15.75 × 1013 J, Energy, Total energy, Power =, ⇒t =, Time, Power, 15.75 × 1013, ⇒ t=, = 1.96 × 1011s, 800, =, , =, , 1.96 × 1011, = 6.2 × 103 years, 365 × 24 × 60 × 60, , 4, 18. , He + 4He → 8Be + Q, (i) Dm = 2 × 4.0026 – 8.0053 = 8.0052 – 8.0053, = – 0.0001 amu, (ii) Q = (2mHe – mBe) c 2, MeV, = (2 × 4.0026 – 8.0053)c2 × 931 2, c, = –0.0931 MeV = –93.1 keV, (iii) Since Q is negative, the fusion is not energetically, favourable., 19. , Rate of electrical energy generation is 250 MW, = 250 × 106 W (or J s–1).

Page 12 :
So, electrical energy generation is 250 MW = 250 × 106 W, (or J s–1)., Therefore, electrical energy generated in 1 year is, (250 × 106 J s–1) × (365 × 24 × 60 × 60 s) = 7.884 × 1015 J, Thermal energy from fission of one 235U nucleus is 200 MeV =, 200 × 1.6 × 10–13 = 3.2 × 10–11 J, Since the efficiency is 25%, the electrical energy obtained from, the fission one 235U nucleus,, 25, E1 = 3.2 × 10 −11 ×, = 8.0 × 10 −12 J, 100, \ The number of fissions of 235U required in one year,, 15, , 7.884 × 10, , = 9.855 × 1026, 8.0 × 10 −12, Number of moles of 235U required per year,, N=, , N=, , 9.855 × 1026, 23, , 6.02 × 10, Therefore, mass of 235U required per year,, m = 1.636 × 103 × 235 = 3.844 × 105 g = 384.4 kg, 20. , We know that binding energy of hydrogen atom in, ground state,, me 4, = 13.6 eV …(i), E =, 8 ∈20 h 2, Replacing e by e′ and m by m′, reduced mass of neutron –, proton,, M × M M 1836m, m′ =, = =, = 918 m , 2, M +M 2, (M = mass of neutron/proton), ,4, Binding energy, E ′ = 918 me = 2.2 MeV ...(ii), 8 ∈20 h 2, Dividing eq. (ii) by (i), we get, , \, , 21., , 6, , 2.2 × 10,  e′, 918   =, e, 13.6, e′, 1/ 4, = (176.21) = 3.64, e, , Nuclear Fission, 1. The process of splitting of 1., a heavy nucleus into two, nuclei of nearly comparable, masses with liberation of, energy is called nuclear, fission., Example:, 235, 1, 92 U +0, , n →141, 56 Ba, , 1, + 92, 36 Kr + 30 n, , +Q, , Nuclear Fusion, When two or more, than two light nuclei, fuse together to form, heavy nucleus with the, liberation of energy, the, process is called nuclear, fusion., Example:, 2, 2, 4, 1 H +1 H →2, , 2. The lighter nuclei have, to be brought very close, to each other against, electrostatic repulsion., , 3. The products of nuclear fission 3. The products of nuclear, reaction are radioactive., fusion are not radioactive., 22. , Energy released = Dm × 931 MeV, , ∆m = 4m (11H) − m (24 He), Energy released, Q = [4m (11H) − m (24 He)] × 931MeV, = [4 × 1.007825 – 4.002603] × 931 MeV = 26.72 MeV., 23. , I n a given nuclear reaction, the sum of the masses, of the target nucleus (21H) and the bombarding particle, , = 1.636 × 103, , 4, , 2. A suitable bullet or, projectile like neutron is, needed., , He, + 24 MeV, , ( ), , (21H) may be greater than the product nucleus 3He and, 2, the outgoing neutron 01n. So from the law of conservation of, mass-energy some energy (3.27 MeV) is released due to mass, defect in the nuclear reaction. This energy is called Q-value, of the nuclear reaction., 24. Applying principle of conservation of energy,, 2, , p2 pp, E – B = Kn + Kp = n +, …(i), 2m 2m, From law of conservation of momentum,, pn + pp = E/c, when E = B,, from equation (i), pn = pp = 0, \ Process cannot take place., For process to take place, let E be very slightly bigger than B so, that E = B + l, (l << B.), 2, p2 pp, λ= n +, 2m 2m, 1 2, λ=, [p + ( p p − E /c )2 ], 2m p, , pp =, ,  E2, , E, E, ±, −,  2 − mλ , 2, 2c, 4c,  2c, , , For pp (momentum of proton) to be real, the determinant must, be positive.,  E2, , E2, B2, −, − mλ  ≥ 0 or λ =, , 2  2, 2, , 4c, 2c, 4mc, 4mc 2, E2, , Therefore, for the given process to occur the value of energy E, must be greater than binding energy B by a factor l which is, equal to, , , , B2, 4mc 2, , .