Page 1 :
Electric Charges and Fields, , Chapter 1:, ELECTRIC CHARGES AND FIELDS, Electrostatics is a branch of physics which deals with the study of electric, charge at rest, Or, It is a branch of physics which deals with the study of force, electric field, and potential due to electric charge at rest, What is an electric charge?, Electric charge is a basic property of a body due to which the body, attracts or repels another body., Charge is a scalar quantity.S.I. unit of charge is coulomb (C), Note: Electric charge is best understood by what it does and not by what it is, Types of charges: There are two types, 1) Positive charge, 2) Negative charge, By convention:, The charge on proton is taken as positive charge., The charge on electron is taken as negative charge., Note: Old convention, 1. Charge on glass rod is called positive charge, Charge on plastic rod is called, negative charge, 2. The charges were named as positive and negative by an American scientist, Benzamin Franckline., Neutral body or uncharged body: The body is said to be neutral if it has no, charge. Ex: Atom, Charged body or electrified body:The body is said to be charged if it has net, charge Ex: Ion, Polarity of charge:, The property which differentiate the two types of charges is called, polarity of charge., Note:, 1. When two bodies are rubbed together, then electrons are transferred from, one body to another body. The body which looses an electron becomes, positively charged body and the body which gains an electrons becomes, negatively charged body, 2. Addition of electrons gives negatively charged body and removal of electrons, gives positively charged body., , 1

Page 2 :
Electric Charges and Fields, , 3. When the substance listed in column (1) are rubbed with the substances, listed in column (2). Then the substances in column (1) acquire the positive, charge and the substance in column(2) acquires negative charge., Column (1) (+ve charge), Column (2) (ve charge), Glass rod, Silk cloth, Cat skin or fur, Ebonite rod, Woollen cloth, Amber rod, Woollen cloth, Plastic, Woollen cloth, rubber, 4. Thales of Miletus was the first scientist who discovered the fact that an, amber rubbed with silk or wool attracts the light objects. It was around 600, B.C., 5. Mass of a body is always is positive, whereas charge can be either positive, or negative., Electroscope: It is a device used to detect the charge on a body., Gold leaf electroscope:, It is one type of electroscope used to detect charge on a body., , Construction:, It is one type of electroscope used to detect the charge on a body. It, consists of a vertical metal rod kept on a box.A metal knob is present at the, upper end and gold leaves are attached at bottom end of a metal rod.When a, charged body touches the metal knob, the charge flows to the gold leaves and, gold leaves diverge (repelled).The degree of divergence of leaves depends on, charge on a body., Conductor:The substance which allows the charges to pass through it easily is, called conductor, Ex:All metals (Cu, Al, Ag, Fe etc…), thehumanbody, animal body and earth., Insulator: The substance which doesnot allow the charges to pass through it is, called insulator., Ex:Wood, plastic, Diamond, Glass, , 2

Page 3 :
Electric Charges and Fields, , Note (1): When a conductor is charged then charges are distributed over the, entire surface of the conductor, Ex:, , Negatively charged conductor, , Positively charged conductor, , Note(2): If some charge is put on an insulator, it stay at the same place, Ex:, , Negatively charged Insulator, , Positively charged Insulator, , That is the charge doesn’t get distributed over the surface of insulator., Electrification:The process of charging a body is called electrification., Earthing or Grounding:, The process of sharing the charges with the earth is called earthing or, grounding., Ex 1):When a negatively charged body is connected to earth,, then the electrons flow from body to earth till the body, becomes neutral., , Ex 2):When a positively charged body is connected to earth,, then the electron flow from earth to body till the body becomes, neutral., , Ex 3):When a neutral body is connected to earth, then there is, no flow of charge from body to earth., , Earthing is necessary for house, why?, The electricity from the mains is supplied to our houses using a 3 core, wiring called live wire, neutral wire and earth wire., The live and neutral wires carry the current from the power station. One, end of the earth wire is connected to a thick metal plate which is buried in the, earth and the other end of earth wire is connected to metallic bodies of, electrical appliances (refrigerator, T.V, etc)., When live wire touches the metallic body then charges flow to the earth, through earth wire.Therefore, there is no damages to the electrical appliances., 3

Page 4 :
Electric Charges and Fields, , Note:, 1. Usually the live wire is red in colour neutral wire is black in colour and the, earth wire is green in colour., Methods of charging a body, There are three methods to charge a body, a) Charging by friction, b) Charging by conduction, c) Charging by induction, Charging by friction:, When a glass rod is rubbed with silk cloth then glass rod loses the, electron and silk cloth gains electron therefore glass rod becomes positively, charged body and the silkcloth becomesnegatively charged body. This process, is called charging by friction, Note:Normally insulator can be charged by friction method. In this method, opposite charges are developed., Charging by conduction:, A, , B, , A, , B, , A, , B, , (b), , (a), , (c), Let A and B are the two conductors A is negatively charged and B is, neutral when A and B are brought in contact, free electrons flow from A to B, therefore conductor B gets negatively charged.This process is called charging, by conduction., Note:Charging by conduction is suitable for conductors. In this method same, charges are developed., Charging by Induction:, When a charged body is brought near the neutral body then opposite, charges are developed on a near surface of a neutral body. This process is, called charging by Induction, Describe how two spheres can oppositely charged by induction method, , (e), , The two metal spheres can be oppositely charged by following step:, Step 1:Bring two metal spheres A and B in contact mounted on insulating, stand as shown in fig (a)., 4

Page 5 :
Electric Charges and Fields, , Step 2:Bring a positively charged glass rod near the sphere A. Then the free, electrons in A and B are attracted towards glass rod. As a result excess, negative charges and positive charges are developed on A and B as shown in fig, (b)., Step 3: Separate the spheres A and B by a small distance while the glass rod is, held near ‘A’ as shown in fig (c)., Step 4:Remove the glassrod, the negative charges on A and positive charges on, ‘B’ are uniformly distributed as shown in fig (d)., By induction method the two metal spheres acquired equal and opposite, charges, Note: Charging by induction is suitable for conductors. In this method, opposite charges are developed., Note:, Describe how canyou charge a single metal sphere positively without, touching it (i.e. by induction), , (a), , (b), , (c), , (d), , The metallic sphere can be positively charged by following steps, Step 1:Consider a neutral metal sphere kept on insulating stand as shown in, fig (a)., Step 2:Bring a negatively charged plastic rod near the sphere. Then free, electrons move away from the rod due to repulsion. As a result excess, positively and negatively charges are developed (induced) on the sphere as, shown in fig (b), Step 3:negatively charged part of a sphere is connected to earth, withoutremoving plasticrod, then electrons flow into earth as shown in fig (c)., Step 4: Remove the plasticrod and earthing, now positive charges are, distributed over the surface of sphere as shown in fig (d)., i.e. Metallic sphere is positively charged by induction method, Note:, 1. Similar steps are involved on charging a metal sphere negatively by bringing, a positively charged glass rod., 2. Why charged body attracts light objects?, When a charged body is brought near the light objects like piece of, paper, the charged body induces opposite charges on near surface of a light, objects. As a result charged body attracts light objects., , 5

Page 6 :
Electric Charges and Fields, , What are Point charges?, Charges whose sizes are very small compared to the distance between them are, called point charges., Basic unit of charge or elementary charge or fundamental charge, The charge on an electron or proton is called basic unit of charge or, elementary charge, It is denoted by the letter ‘e’, The value of elementary charge is e=1.602192  10-19C, Note:, 1) Charge on electron= e = 1.602  10-19C., 2) Charge on proton = +e = +1.602 × 1019C, Magnitude of charge on electron and proton is equal, 3) Charge on neutron = 0, 4) The least possible amount of charge that can exist independently in the, nature is called elementary charge., Basic properties of electric charge:, 1. The electric charge is conserved., 2. The electric charge is quantized., 3. The charge is additive., 4. Like charges repel each other and unlike charges attract each other., 5. Charge is scalar, its SI unit is coulomb., Explain Additivity of charge:, Charges can be added algebraically, i.e., if a system contains positive, charges q1 ,  q 2 ,  q 3 and negative charges q 4 ,  q 5 ,  q 6 ., Then, total charges of a system or net charge = q1  q 2  q3  q 4  q 5  q 6 ., Ex: If a system contains the charges +4C, +2C, 3C and 1C, Then, net charge = 4C+2C3C1C=+2C, Explain Conservation of charge:, Conservation of charge states that “The total charge of an isolated, system remains always constant”, i.e. total charge of the isolated system can, neither be created nor be destroyed but there is a transfer of electrons from one, body to another body.Therefore charge is conserved., Ex:In unstable nucleus neutron is converted into proton and electron., i.e, neutron = proton + electron, A/C to law of conservation of charge,, Charge on neutron = charge on proton + charge on electron, 0 = +e – e, 0=0, Explain Quantization of charge:, The charge on a body is always an integral multiple of charge on electron.,  Quantization of charge means charge on a body can be increased or, decreased in steps of ‘e’, 6

Page 7 :
Electric Charges and Fields, ,  Charge on a body is given by (Expression for quantization of charge), q=n e, Where, n= number of electrons added or removed from the body, Where,q= charge on a body, e=elementary charge, Note:, 1. Quantization of charge was experimentally demonstrated by R.A Millikan, through his oil-drop experiment., 2. Quantization of charge was first suggested by the experimental laws of, electrolysis discovered by Faraday., 3. The force of attraction or repulsion between two charges at restis called, electrostatic force., State and explain coulomb’s law:, It states that “the force between two point charges is directly proportional, to the product of magnitudes of two chargesand inversely proportional to, square of the distance between them. The force is acting along the line joining, two charges.”, r, , q1, Let,, , q2, , q1 and q 2 = two point charges, r = distance between them,, F = force between q1 and q2, F  q1q 2, , and, , F, , 1, r2, , q1q 2, r2, qq, F = K 12 2, r, F, , Where, K = proportionality constant, , 1, 40, 1 q1q 2, F, 40 r 2, , but, K =, , This is the expression for electrostatic force or columb’s law, Note 1:  0 is called permittivity of free space, S.I unit is C2 N-1 m-2,  0 = 8.854  10-12C2 N-1 m-2, , 1, 40, 1, 1, , 40 4  3.14  8.854 1012, , Note2:To find the value of, , 7

Page 8 :
Electric Charges and Fields, , 1, = 0.00899  1012, 40, 1, = 8.99  109, 40, 1, = 9  109Nm2/c2, 40, Note3: Coulomb used a Torsion balance for measuring the force between two, charged metallic spheres., Note4:Torsion balance is a sensitive device to measure a force., Note5:Cavandis also used Torsion balance to measure the very feeble, gravitational force., Define one columb using coulomb’s law:, According to coulomb’s law, 1 q1q 2, F, if q1=q2=1C and r=1m, 4 0 r, 1 1 1, F, Then, 4 0 12, 1, F, 4 0, F=9×109 N, Definition:One columb is the charge that when placed at a distance of 1m from, another identical charge kept in vacuum experiences a force of repulsion of, 9×109N., Note:, Define one coulomb of charge in terms of current:, One coulomb is that charge flowing through a wire in one second if the, current is one ampere., Columb’s law in vector form:, r, 1 q1q 2, F21 , rˆ21, 4 0 r212, Where,, r, F21  Force on q 2 by q1, r, r21 = position vector., , q1, , r, F12, , r, r r, r21  r2  r1, , r, r1, , r̂21 = unit vector which gives direction of force., Note:1) The force on q2 and q1 = force on q1 by q2, r, r, F21  F12, Thus,Coulomb’s law obeys Newton’s III law., , 8, , q2, r, r2, , r, F21

Page 10 :
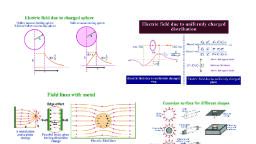
Electric Charges and Fields, , Electric field or electric field intensity or strength:, Electric field at a point is the force per unit positive charge., Force, i.e. Electric field=, unit positive charge, F, E, q0, S.I. unit is newton/coulomb(N/C)or volt / meter (v/m),, Electric field is a vector quantity., Source charge: The charge which produces the electric field is called source, charge., Test charge: The charge that detects the effect of source charge is called test, charge., Note: UPC=Unit positive charge. In SI, UPC = 1 coulomb., Mention the expression for electric field due to a point charge:, q, , q0, P, r, Let, q=source charge, q0=test charge (upc), P=any point, According to coulomb’s law, qq, 1, F,  20,  0 r, F, 1, q, ,  2, q 0  0 r, F,  E  Elecric field, But, q0, 1, q, E,  2, , 4 0 r, This is the expression for electric field at a point p due to a charge., Note:, r, 1. Electric field in vector form: E , , 2., , 3., , +q, , 1, q,  2 rˆ, 4 0 r, , +, , r, E, The electric field due to positive charge is directed radially outward., , , , -q, r, E, , The electric field due to negative charge is directed radially inward., , 10

Page 11 :
Electric Charges and Fields, , Principle of superposition of electric field:, It’s state that “The net electric field at a point is the vector sum of all the, electric fields at that point due to number of charges.”, Application of principle of superposition to find Electric field due to, system of charges:, Consider a system of ‘n’ charges, arranged as shown., Electric field at a point P by q1 charge is, r, q, 1, E1P ,  21 rˆ1P, 4 0 r1P, Electric field at a point P by q2 charge is, r, q, 1, E 2P ,  22 rˆ2P, 4 0 r2P, Similarly, r, q, 1, E 3P ,  23 rˆ3P, 4 0 r3P, r, q, 1, E nP ,  2n rˆnp, 4 0 rnP, According to principle of superposition net electric field at P, r, r, r, r, r, EP  E1P  E2P  E3P  .........  E nP, r, q, q, q, 1, 1, 1, EP ,  21 rˆ1P ,  22 rˆ2P  .......... ,  2n rˆnP, 4 0 r1P, 4 0 r2P, 4 0 rnP, r, q2, qn , 1  q1, EP ,  2 rˆ1P  2 rˆ2P  ..........  2 rˆnP , 40  r1P, r2P, rnP , n, r, qi, 1, EP , rˆiP, , 40 i 1 riP2, Physical significance of electric field:, Electric field is a vector quantity. Electric field was first introduced by, Faraday. Electric field transport the energy. It is a characteristic of system of, charges and it does not depend on test charge. It deals with theelectromagnetic, phenomena., Electricfield lines or Electric lines of force:, It is a curved path drawn such that tangent at any point on it gives the, direction of net electric field at that point., Or, It is an imaginary path along which unit positive charge moves., The concepts of electric field lines was developed by Faraday., , 11

Page 12 :
Electric Charges and Fields, , Note:, 1. Electric field lines due to a single positive charge are, directed radially outward., 2. Electric field lines due to a single negative charge are, directed radially onward., , 3. The electric field lines around two opposite charges are as, shown in figure., , 4. The electric field lines around two same charges are as, shown., Properties of electric, 1. The electric field, charge., 2. The electric field, 3. The electric field, 4. The electric field, , field lines:, lines start from the positive charge and ends at negative, lines donot intersect each other., lines donot form a closed loop., lines are normal to the surface of charged conductor., , Note: If electric field lines intersect, the field at the point of intersection will not, have a unique direction. That’s why two electric field lines never intersect., Electric flux:, The total number of electric field lines passing through the surface area, held perpendicular to the direction of field lines is called electric flux., S.I unit is NC-1 m2., Electric flux is a scalar quantity., Electric flux through an area element:, , Consider a surface ‘S’., Let, S = small area element of surface ‘S’, E = Electric field,  = Angle between ‘E’ and normal to S, 12

Page 13 :
Electric Charges and Fields, ,  = Electric flux through S ., The projection of area ‘ S ’ normal to E is given by S cos, The electric flux through the area element S is given by,  = E S cos,  ,   E  S, Therefore, electric flux through a surface is defined as the dot product of, electric field and area element., , Note 1) Electric flux through small area S is given by,   ES cos ,  ,   E  S, Note 2) Total electric flux through entire surface is given,  ,  ,    E  S, or    E  S, Note 3) We have  = E S cos, , E , S cos`, i.e. Electric field is the electric flux per unit normal area., , If  = 00,, cos00 = 1, then E , S, 0, 0, Note 4) If   0 , cos0  1, ,   EScos 00,   ES, i.e. flux is maximum, Note 5)If   900 , cos900  0, Then,   ES  0 =0, i.e. flux is minimum., Electric dipole:A set of two equal and opposite point charges separated by a, small distance is called electric dipole., +q and q = point charges, q, +q, 2a = distance between +q and q, = dipole length, 2a, Note: Net charge of an electric dipole is zero, , 13

Page 14 :
Electric Charges and Fields, , , Electric dipole moment P :, It is the product of magnitude of one of the charges and the distance between, two charges of dipole., Dipolemoment = charge × distance, P  q  2a, S.I unit is coulomb × metre (Cm), Dipole moment is a vector quantity, , , , Note (1) Dipole moment in vector form, , p  q  2a P̂, Where P̂ = unit vector which gives direction of dipole moment., Note (2) The direction of dipole moment is directed from negative charge to, positive charge along the dipole axis, , Note (3), , Obtain an expression for the electric field at a point along the axis of, dipole, , Consider a point M on the axis of electric dipole., Let O = mid point of dipole, +q and q = two point charges,, q = magnitude of point charge, 2a, r = distance between O rand M, r = dipole length,, P = dipole moment acting from q to +q, P̂ = unit vector of P, but P = q × 2a ------------> (1), Electric field at M due to +q charge is, , 1, q, E q , , P̂, away from +q, ------------- (2), 40 r  a 2, Electric field at M due to q charge is, 14

Page 15 :
Electric Charges and Fields, , r, 1, q, towards q, Eq  , , Pˆ, 40  r  a 2, , , (ve sign indicates that E q is opposite to P ), , According to the principle of superposition the total electric field at M is,  , , E  E q  E q, , 1, q, 1, q, E, , P̂ , , P̂, 2, 40 r  a , 40 r  a 2, , q  1, 1 , E, , ,  P̂, 2, 40  r  a  r  a 2 , 2, 2, , , r, r  a   r  a , , q  4ar  ˆ, 1, 1, E, P, , , 2, 2, 2, 2, 40  r 2  a 2 2 , r  a  r  a , r  a  r  a , , , , , , , , If,, , , , r>>a, , =, , then r 2  a 2   r 2   r 4, , q  4ar , E , P̂, 40  r 4 , 2, , =, , 2, , r 2  a 2  2ar  r 2  a 2  2ar, r  a 2 r  a 2, 4ar, , r, , 2, ,  a2, , , , 2, , q  4a ,   P̂, 40  r 3 , , , E, , 1  2  2a  q ,  P̂, 40  r 3, , 1  2P , E, P̂, 40  r 3 , This is the expression for electric field at a point on the axis of dipole., Obtain an expression for the electric field at a point on the equatorial, plane of electric dipole., , Consider a point M on the perpendicular bisector of the axis of dipole., Let O = Midpoint of dipoles, +q and q = two point charges, q = magnitude of charge,, 2a = dipole length, 15

Page 16 :
Electric Charges and Fields, , P = dipole moment acting from q to +q,, P̂ = unit vector, Magnitude of dipole moment is, P = q × 2a ------ (1), From figure,, AM2 = r2 + a2, and BM2 = r2 + a2, 2, 2, 2,  AM = BM = r + a2, AM = BM = r 2  a 2 2, Electric field at M due to +q charge is, 1, , ur, 1, q, Eq , , pˆ, 40 AM 2, ur, 1, q, Eq ,  2, Pˆ, 40  r  a 2 , , away from +q, , Electric field at M due to q charge is, , ur, 1, q, Eq , , pˆ, 40 BM 2, ur, 1, q, towards q, Eq ,  2, Pˆ, 4 0  r  a 2 , ur, ur, Hence E  q  E  q, (magnitudes), ur, ur, Resolving E  q and E  q in to two rectangular components each. Here,, perpendicular components are equal and opposite. So they cancels each other., The components parallel to dipole axis are in same direction. So they add up, Total electric field at M, , ur, ur, ur, E    E  q cos   E  q cos  , , , , [ve sign indicates that E is opposite to P ], , ur, ur, ur, E    E  q  E  q  cos , ,  1, , q, 1, q,  ,  2 2 Pˆ ,  2 2 Pˆ  cos , 40 r  a,  40 r  a, , , , , , , , , , , , , ur, 2q,  Pˆ, E  , cos, , 2, 2,  40  r  a , , But from figure,, AO, cos  , , AM, , a, , r, , 2, , a, , 1, 2 2, , , , , ur, 2q, a, , E   , , 2, 2,  40 r  a, r2  a2, , , , ,  , , 16, , , , , ˆ, P, 1 , 2 , , ,  P  q  2a 

Page 17 :
Electric Charges and Fields, , , ur, 1 , P, E, , 40,  r2  a2, , , , , , , If r>>a then r 2  a 2, , , ˆ, P, 3 , 2 , , , ,  ; r , 3, , 2, , 2, , 3, , 2, ,  r3, , 1 Pˆ, P, 40  r 3 , This is the expression for electric field at a point on the equatorial plane., E  , , Note (1)Electric field at a point on the dipole axis., ur, 1  2P  ˆ, E dipoleaxies ,  P, 40  r 3 , It is acting along dipole moment, Note (2)Electric field at a point on the equatorial plane, ur, 1  Pˆ, E equatorial  ,  P, 40  r 3 , ve sign indicates that net electric field is opposite to dipole moment, Note (3): From note (1) and (2). It is clear that, Edipole axis = 2 Equatorial, (magnitude wise), Note (4) : Force acting on positive charge is along the electric field direction., The force acting on negative charge is opposite to the field direction., Obtain the expression for the torque acting on an electric dipole placed in, a uniform electric field:, , Consider an electric dipole placed in a uniform electric field ‘E’., Let +q and q = two charges of dipole, AB = 2a = dipole length, r, r,  = angle between E and dipole moment P ., The fore acting on +q is, r, F+q=qE, along E, The force acting on –q is, r, F q  qE, opposite to E, i.e. F q and F q are two equal and opposite force acting on the dipole. As a, result, torque is acting on the dipole, but,, torque = force × perpendicular distance between two forces.,   qE  BC ----- (1), From right angled triangle BCA, 17

Page 18 :
Electric Charges and Fields, , BC BC, , AB 2a, , BC = 2a sin, equation (1) becomes,   q  2a  E  sin , , sin =, ,   P E sin , , Q q  2a  P , , This is the expression for torque acting on the dipole, = P E sin, r r r,   P  E  Vector form, i.e. Torque is the cross product of dipole moment and electric field,, Torque is a vector., S.I unit of torque is Nm (newtonmetre), , Note-1:We have, , Note-2: If dipole is along the electric field, Then  = 00 Or  = 1800, , Then sin = sin00 = sin1800 = 0,  = PE × sin, = PE × 0, = 0, i.e no torque is acted on dipole (Torque is minimum), Note-3:, If dipole is perpendicular to Electric field. Then, =900., Then sin = sin 900 = 1,  = P E sin ,  = PE, Torque is maximum when the dipole is placed, perpendicular to the direction of field., Linear charge density ():, It is defined as the charge per unit length., charge, i.e, Linear charge density =, length, q, , L, S.I unit is coulomb/metre (c/m), , 18

Page 19 :
Electric Charges and Fields, , Surface charge density ():, It is defined as the charge per unit area, charge, i.e. surface charge density =, area, q, , S, S.I unit is C/m2, Volume charge density ():, It is defined as the charge per unit volume, charge, i.e. volume charge density =, Volume, q, , V, S.I unit is C/m3, Mention the expression for electric field due to continuous charge, distribution, Electric field due to  q charge present in small volume element V is, 1, q,  2  (1), E =, 4 0 r, q, But  ,  = volume charge density, V, q  V, - equation (1) become, 1, V, E ,  2, 4 0, r, Electric field due to entire volume V is, E   E, all V, , E, , 1, 40, , V, 2, all V r, , , , This is the expression for electric field due to continuous charge distribution., State Gauss law:, It states that “Total electric flux flow through the closed surface is equal, to, , q, ., 0, That is, Total electric flux , , Where,, , q, 0, , q=total charge closed by the surface, 0= permittivity of free space., , 19

Page 20 :
Electric Charges and Fields, , Deduce Gauss law:, Consider a sphere of radius ‘r’, divide the sphere into small area element as, shown in figure., Let,, , q = charge enclosed by a sphere,, r = radius of sphere., s = small area element, , Electric field at the surface is, , E, , 1 q, 40 r 2, , Small electric flux flows through S is, ,   EScos  ,, , but  = 0°, cos0° = 1, ,    ES, ,  , , 1 q, S, 40 r 2, ,  Total electric flux through entire sphere., ,    , , , , 1, q,  2 S, 4 0 r, , 1, q,  2  S, 40 r, , But, ,  S  4r, , , , , , 2, ,  area of sphere, , 1, q,  2  4r 2, 40 r, , , q, 0, , This is called Gauss law., , 20

Page 21 :
Electric Charges and Fields, , Significance of Gauss law:, 1. Gauss law is true for any closed surface, no matter what its shape or size., 2. According to Gauss law,  , , q, here q is the sum of all the charges enclosed, 0, , by the surface., 3. The surface that we choose for the application of gauss law is called, Gaussian surface., 4. Gauss law is based on inverse square dependence on distance contained in, coulombs law., Applications of Gauss law: Using Gauss law, 1. Electric field due to infinite long straight uniformly charged wire can be, found., 2. Electric field due to uniformly charged infinite sheet can be found., 3. Electric field due to a charged thin spherical shell can be found., Derive an expression for electric field due to infinitely long straight, uniformly charged wire using Gauss law:, Normal to S, 1, , =900, , E, 1, , E, no, =0, 3, r, 3, L, nor, m to S E, Normal, P, E, r, mal, al, no, no, no, to, to, Gaussian, surface, r, r, r, S, m, 2, m, m, S, al, E, 0, al, al, =90, to, no, to E, to, 2, r, , , Normal to S, , m, S, S, S, al, Consider an infinitely long straight charged wire., Let  = Linear charge density of wire, E=Electric field at atopoint ‘P’, , r = Distance between wire and P., S, Draw a cylindrical Gaussian surface of radius ‘r’ passing through point ‘P’ a, shown in figure., The electric field is radially outward. i.e. perpendicular to wire., Electric flux through 1st circular end of a cylinder (Gaussian surface) is, 21

Page 22 :
Electric Charges and Fields, , 1 =ES cos, But =900 cos900=0, 1=0, Similarly electric flux through 2nd circular end of cylinder (G.S.) is, 2= 0, Electric flux through curved surface of cylinder (Gaussian surface) is, 3=ES cos, =00, cos00=1, 3 = ES, But, S = 2rL = Total surface area of cylinder, Where, L=length of cylinder., 3=E2rL, Total electric flux is, =1+2+3, =0+0+ E2rL, =E2rL -------------- (1), Let, q= charge enclosed by cylinder (Gaussian surface), But, , Charge, Length, q, , L, , , q=L, According to Gauss law, , q, 0, L, --------------- (2), , 0, , , , From equation (1) and (2), , E  2rL , , E, , L, 0, , , 20 r, , This is the expression for electric field due to a charged long wire., , r, , Note: 1) In vector form, E , , , rˆ ,, 20 r, , r, r̂ = unit vector which gives directions of E and it is radially directed., Note: 2) Electric field due to a wire is radially outward if charge is +ve (or  is, +ve). Electric field due to a wire is radially inward if charge is negative (or  is, negative):, 22

Page 23 :
Electric Charges and Fields, , Derive an expression for electric field due to a uniformly charged infinite, plane sheet:, , P, E, , E, , G.S., norm, al to, Plane sheet, S, Consider a uniformly charged infinite plane sheet., Let, = surface charge density of plane sheet, E=Electric field at a point P due to plane sheet, it is directed outward., Draw a cylindrical Gaussian surface, perpendicular to plane sheet, passing through a point ‘P’ as shown in figure., Let, A=cross sectional area of cylinder., Electric flux through 1st circular end of cylinder (Gaussian surface) is, 1= ES cos, But, S=A, =00, cos00=1, , 1=EA, Similarly, electric flux through 2nd circular end of cylinder is, 2=EA, Electric flux through curved surface of cylinder is, 3= ES cos, =900, cos900=0, , 3= ES  0, 3=0, Total electric flux through cylinder (Gaussian surface) is, =1+2+3, =EA+EA+0, =2EA -------------- (1), Charge enclosed by cylinder = q, But, , Charge, Area, q, , , A, , , q= A, , According to Gauss law, , q, 0, A, ------------- (2), , 0, , , 23

Page 24 :
Electric Charges and Fields, , From equations (1) and (2), , 2EA , , E, , A, 0, , , 20, , This is the expression for electric field due to plane sheet., Note:, , r, , 1. In vector form E , , , nˆ . Where n̂  unit vector., 20, , 2. E is directed outward if  is +ve (i.e. q is +ve) and E is directed inward if  is, negative (i.e. q is negative)., 3. E is independent of distance from plane sheet., Derive an expression for electric field due to a charged thin spherical, shell using Gauss law:, Case 1: Electric field outside the shell:, , Consider a charged thin spherical shell., Let, R= radius of spherical shell,, E= electric field at a point ‘P’,, Area of spherical shell = 4R2, , , q=charge on spherical shell, =surface charge density, , charge, area, q, , 4R 2, , , , q=4R2----------- (1), Consider a point P out side the shell. Imagine that a spherical Gaussian, surface around the shell passing through point ‘P’ with the centre ‘O’ as shown, in figure.,  r=radius of Gaussian surface, Let S=small area element around point ‘P’,  The electric flux through S is, 24

Page 25 :
Electric Charges and Fields, , =ES cos, But =0, cos0=1, =ES, Total electric flux through entire Gaussian surface is, ,    , ,    ES, ,   E S (Electric field E is same at all point on Gaussian surface), But, ,  S  r, , 2, , = area of Gaussian surface., ,   E  4r 2 -------------- (2), According to Gauss law, , , , q, 0, , [ from equation (1), q=4R2], , 4R 2, ----------- (3), , 0, From equations (1) and (2),, , E  4r 2 , , E, , 4R 2, 0, , R 2, 0 r 2, , This is the expression for electric field at a point ‘P’, Case 2:Electric field inside the shell:, Consider a point P inside the spherical shell. Consider a Gaussian, surface passing through point ‘P’ as shown in figure., Electric flux through the Gaussian surface is, ,   E  4r 2 (Refer equation 2), According to Gauss law,  , , q, 0, , E  4r 2 , , q, 0, , Charge enclosed by Gaussian surface. i.e. q=0., (No charge is present inside the shell), E=0, i.e. Electric field due to a uniformly charged thin spherical shell is zero at all, point inside the shell., , 25

Page 26 :
Electric Charges and Fields, ,  R, 0 r 2, q, , 4R 2, q,  R2, 2, E  4R 2, 0 r, q, E, 40 r 2, 1 q, E, 40 r 2, E, , Note:, But, , 2, , This is the expression for electric field at a point out side the charged, spherical shell., One mark questions, 1. What is an electric charge?, 2. What are point charges?, 3. Define polarity of charge., 4. What is gold leaf electro scope?, 5. What is meant by earthing?, 6. What is significance of earthing?, 7. Define elementary charge., 8. What is meant by additivity of charge?, 9. The net charge of a system of point charges -4, +3, -1 & +4 (S.I.units) =?, 10. What is meant by conservation of charge?, 11. What is quantisation of charge?, 12. Mention the S.I. unit of charge. (March-2014), 13. State coulomb’s law (March-2017), 14. Define one coulomb of charge. (March-2015), 15. State the principal of super position of electro statics., 16. Which principle is employed in finding the force between multiple charges?, 17. Define electric field., 18. Is electric field a scalar/vector?, 19. Mention the S.I. unit of electric field., 20. What is the direction of electric field due to a point positive charge, 21. What is the direction of electric field due to a point negative charge?, 22. What is a source charge?, 23. What is a test charge?, 24. How do you pictorially map the electric field around a configuration of, charges?, 25. What is an electric field line?, 26. What is electric flux?, 27. Mention the S.I.unit of electric flux., 28. What is an electric dipole?, 29. What is the net charge of an electric dipole? Define dipole moment., 26

Page 27 :
Electric Charges and Fields, , 30. Is dipole moment a vector / scalar?, 31. What is the direction of dipole moment?, 32. What is the net force on an electric dipole placed in a uniform electric field?, 33. When is the torque acting on an electric dipole placed in a uniform electric, , field maximum?, 34. When is the torque acting on an electric dipole placed in a uniform electric, field minimum?, 35. State Gauss’s law., 36. What is a Gaussian surface?, 37. What happens to the force between two point charges if the distance, between them is doubled?, 38. If two charges kept in ‘air’ at a certain separation, are now kept at the same, separation in ‘water’ of dielectric constant 80, then what happens to the, force between them?, 39. On a macroscopic scale is charge discrete or continuous?, Two mark questions, 1. Explain construction of gold leaf electroscope., 2. Earthing is necessary for house, Why?, 3. Write the expression for quantisation of charge and explain the terms in it., 4. State and explain Coulomb’s law of electrostatics. (March-2014, July-2015,, March-2017), 5. Write Coulomb’s law in vector notation and explain the terms. (March-2015), 6. Write the pictorial representations of the force of repulsion and attraction,, between two point charges., 7. Explain the principle of superposition to calculate the force between, multiple charges., 8. Mention the expression for the electric field due to a point charge placed in, vacuum., 9. Write the expression for the electric field due to a system of charges and, explain it., 10. Draw electric field lines in case of a positive point charge., 11. Sketch electric field lines in case of a negative point charge., 12. Sketch the electric field lines in case of an electric dipole., 13. Sketch the electric field lines in case of two equal positive point charges., 14. Mention any two properties of electric field lines. (July-2015, March-2015,, March-2017), 15. Write the expression for the torque acting on an electric dipole placed in a, uniform electric field and explain the terms in it., 16. Define linear density of charge and mention its SI unit., 17. Define surface density of charge and mention its SI unit., 18. Define volume density of charge and mention its SI unit., 19. What is the effect of a non-uniform electric field on an electric dipole?, Three mark questions, 1. Mention three properties of electric charge. (July-2014), 2. Draw a diagram to show the resultant force on a charge in a system of three, charges., 3. Why is the electric field inside a uniformly charged spherical shell, zero?, Explain., 27

Page 28 :
Electric Charges and Fields, , 4. Obtain the expression for the torque acting on an electric dipole placed in a, uniform electric field., Five mark questions, 1. Obtain an expression for the electric field at a point along the axis of an, electric dipole.(Mar-16), 2. Obtain an expression for the electric field at a point on the equatorial plane, of an electric dipole.(March-2015), 3. State Gauss’s law. Obtain an expression for the electric field due to an, infinitely long straight uniformly charged conductor. (July-2015), 4. State Gauss’s law.Obtain an expression for the electric field due to a, uniformly charged infinite plane sheet., 5. State Gauss’s law.Obtain an expression for the electric field at an outside, point due to a uniformly charged thin spherical shell. (March-2014, July2014)., , 28