Page 3 :
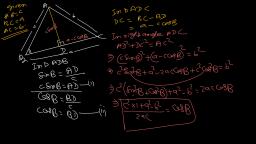
3.3.5 The Cosine Rule : In ABC,, (i) @=b?+c?—2be cosA (ii) b® =c?+a?-2cacosB (iii) c? =a? +b? —2ab cos C, Proof : Take A as the origin, X - axis along AB and the line perpendicular to AB through A as the, Y - axis, The co-ordinates of A, B and C are (0,0). (c, 0) and (b cos A, b sin A) respectively., To prove that a? = b? + c? - 2be cos A, L.H.S. = a? = BC?, = (c—bcos A)?+(0—bsin A) (by distance formula), c?+b? cos?A-—2 becosA+b’ sin? A, c?+ b? cos? A + b? sin? A—2be cos A, = ¢c+b’-2be cosA, = RAS., a =b +c? —2be cosA - Bee, Similarly, we can prove that (0,0), b?=c?+a*— 2cacos B, c? =a? + b?- 2ab cos C Fig 3.5, , C(bcosA,bsinA), , , , Scanned with CamScanner

Page 4 :
3.3.6 The projection Rule: In AABC,, (i) a=bcosC+ccos B, (ii) b=c cos A+acosC, (iii) c=acosB+bcosA, Proof: Here we give proof of onc of these three statements, by considering all possible cases., To prove that a = b cos C +c cos B, Let altitude drawn from A mects BC in D. A, BD is called the peojection of AB on BC., DC is called the projection of AC on BC. e b, Projection of AB on BC =c cos B, And projection of AC on BC = DC = b cos C, , Case (i) B and C are acute angles. B D a Cc, Projection of AB on BC = BD = cc cos B, And projection of AC on BC= DC =b cos C Fig 3.6, , From figure we have,, a =BC=BD+DC, =ccosB+bcosC, =bcosC+ccosB, “a =bcosC+ccosB, Case (ii) B is obtuse angle., *. Projection AB on BC = BD=c cos( 1 - B)=-c cosB, And projection of AC on BC = DC = b cos C, From figure we have,, a =BC=DC-BD, = bcos C -(—c cos B), =bcosC+ccosB, -.a =bcosC+ccosB, Case (iii) B is right angle. In this case D coincides with B., R.HLS. = b cos C+ cos B, = BC+0, = a=LHS., a=bcosC+ccosB, , , , Similarly we can prove the cases where C is obtuse angle and C right angle., Therefore in all possible cases, a= b cos C +¢ cos B, Similarly we can prove other statements,, , Scanned with CamScanner

Page 5 :
not?, , Let's have a theorem., , Theorem 3 : Homogcnous cquation of degree two in x and, , y, ae +2hxy + by? = 0 represents a pair of lines passing, , through the origin if h?- ab > 0., , Proof : Consider the homogencous cquation of degree two, , in x andy, a +2hxy + by? =0 + (1), , Consider two cases b = 0 and b # 0). These two cases are, , exhaustive., , Case 1: If b =0 then equation (1) becomes ax? +2hxy = 0, x(ax +2hy ) =0, which is the combined cquation of, , lines, , , , , , Y ax +2hy=0, , , , , , , , Scanned with CamScanner