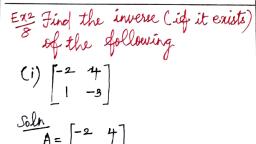Page 1 : www.kalvikadal.in https://mate rial. kalvikadal.in, , Kalvich Safoi's 12" Mathe TN Gui, , Chapter 1, Applications of Matrices and Determinants, , EXERCISE L1, 1, Find the adjoint of the following:, , 3 4 ; 231 2 9 4, (i) > dj}3 4 1 (iii) -]-2 1 2, 372 : 1 22, Solution, : -3, @) Ls 4=| 4, 6 2, Cofactor of A a adjA = a4, 4 -3 -6 -3, Zipdgull, ii) A=/3 4 1, 3), 2, : 8-7 -(6-3) 21-12 1 3 9, Cofactor of A=|—(6-7) (4-3) ~(14-9)]=]1 1 -5, (3-4) -~(2-3) (8-9) =) gl) =i, 1 Wl 8-1, adj(A) =} —, 9 -5 -1, 2 2» |, Gii) Let A =3 61), 1 2.2, , We know that adj(kA) = k”'adjA, , ne 21, “adja = (3) “a 2 1 2, —2 2, 2, 2.1 6, Cofactorof |-2 1 2]/=|-6 3 6, —2 2 -6 6, 6 6 3] {6 6 3 2-21, adj(A) = a|-6 3 6 =5|6 3 -6|=5|2 1-2],, 3 -6 6 3 6 6 F222, 1 Applications of Matrices and Determinants, , Please Send Your Materials & Question Papers to
[email protected] (or) Whatsapp - 9385336929
Page 2 : www.kalvikadal.in https://material.kalvikadal.in =, , ry, , | +, 2. Find the inverse (if it exists) of the following :, |, , , , 231, | @) i 3 di) {1 5 1 (iii) | 3, | 115 372, Solution Let 4 = mart, Li -3, || = 6-4=240, } [-3 -4, : djA =, a |-1 3, Pate) oe, 2|-1 -2, (5 11, (ii) Let 4=]1 5 1, [1 1 5, |A] = 5225-1) -G-1)+(1-5) = 120-4-4 = 112, [24 -4 -4 244 4, Cofactor of A =|-4 24 -4| => adjA=|-4 24 4, ‘|-4 -4 24 4 -4 24, 6 [OBE 6 --1 41, Aa aay A 2 eee eel, rh wit 28, -l -1 6 -1 -l 6, 2314 23,1, (iti) Lettd=/3.4 1] > |4l=|3 4 1/=2, 3 (Te 2 3 72, 1 =3 9 1 3 9, Cofactor of A =|-(6-7) 4-3 -(-14-9)/=]1 1 <5, (3-4) -(@-3) . (8-9) ely od) —I, 1 -E <I Led, adj(A)=|-3 1-1 puted 3. 4 “<y, omens V9 5 4, , cosa 0 sina, 3. If F(@)=| 0 1 0 |, show that [F(@)J = F(-a),, -sina 0 cosa, , Solution, cosa 0 sina, Given that F(a@)=| 0 1° 0, -sine 0 cosa, Applications of Matrices and Determinants 2, , Please Send Your Materials & Question Papers to
[email protected] (or) Whatsapp - 9385336929, hee . Si Sar Br ‘ :
Page 4 : _ www.kalvikadal.in SEE eee https://material.kalvikadal.in =, , \, i!, , | Solution, To prove 47, AL!, It is enough to prove 4A”, AA?, Hence proved., 6. If A= ., -5, Solution, | adjA =, Hl, Aadiay =| 8, er a, 3 4, djA)A =, wa], , From the above two results,, | A(adjA) = (adjA)A, , 3 2 =] 283, 7. If A= I, E s] [; Ft., , Solution, , a, , 8 +, => 3, , wy, = As, =/, , -g 1 41-84 }, -1l4, 4:7)1 4 3, 81), _g 4{f4 7 4, , g1 0 0] {1 9 0, =+ho g1 of={0 1 Of=7, 81/9 9 81] [0 0 1, , 4), 3 | verify that A(adjA) = (adjd)A=|4\/., , J he, , qa, , 3 4, 5 8, , f, I:, , 0, , =|Ar., , verify that (4B) = BA",, , |A| = 15-14=1#0 |B|=-2+15=1340, , eal, , 5 1, , “2B, , 2 3, , [3, , we 2 [7, 7 5\5 2] las -11, | | |AB] = -77+90=13, h- a 1f-ll 5, ABY = ., (48) ae ‘|: -l), pia = 11" “ll: -2] _1f10-21 449, 13[-5 -1][-7 3} 13]-2547 10-3, , |, |, , i, | Applications of Matrices and Determinants, |, , 4, , | _ |. Please Send Your Materials & Question Papers to
[email protected] (or) Whatsapp - 9385336929
Page 5 : www.kalvikadal.in https://material.kalvikadal.in, , _ Af 5]: (2), 13|-18 7, From (1) and(2) (4B)' = Bt",, 2-4 2, 8. If adj(4)=|-3 12 -7], find A., 2 0 2, Solution adja] = 2[24-0]-(4)[-6-14]+2[0+24] = 16, 24 20 4 7, , adj(adjA) =|-(-8-0) (444) ~(0-8), (28-24) ~(-14+6) (24-12), , , , 24 20 247 [24 8 4 6 2, =|8 8 8|=|20 8 8|=4!5 2, 4 8 12 248 12 6 2, 1, A=t adjA, ladia ), , , , i6, 0 20, 9. If adj(4)=| 6 2 -6|, find 47., 3°06, 0 2 0, Solution » adil = 2 -6|=2(36-18) =36, 3 0 6, 1, At=t (adjA), (adja), 5 [O29 020, tp] 6 2 6 = 41|6 a” 6, 3 0 6 “30 6, , Solution, , Applications of Matrices and Determinants, , ¥ i
[email protected] (or) Whatsapp - 9385336929