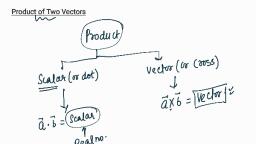
Page 1 :
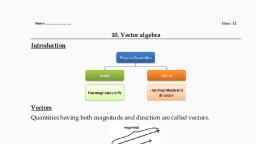
Vectors VELIOR ALGEBRA ~, , , , **The point A from where the vector starts is called its initial point, and, the point B where it ends is called its terminal point. The distance, , between initial and terminal points-af a vector is called the magnitude (or, length) of the vector, denoted a 58) or |a|. The arrow indicates the, direction of th ofvector.)

Page 2 :
Some Basic Concepts, , / Directed line, , Let ‘I’ be any straight line in plane or three dimensional space. This line, can be given two directions by means of arrowheads. A line with one of, these directions prescribed is called a directed line. Une’, , , , , , , , Ne sia, wh, yo” a 7 2, D A B”, , / Position Vector, Consider a point P in space, having coordinates (x, y, z) with, respect to the origin O (0, 0, 0). Then, the vector having O and P as its, initial and terminal points, respectively, is called the position vector of the, point P with respect to O., nw, , i a, , —, OY, ¢ or} c yeder pe

Page 3 :
Consider the position vector of a point P(x, y, Z) as in-F2668. The angles, a, B, Y made by the vector with the positive directions of x, y and z-axes, , respectively, are called its direction angles. “, —______, , The cosine values of these angles, i.e., cosa, cosB and cos y are called, direction cosines of the vector , and usually denoted by I, mand n,, , , , 4, , Thus, the coordinates of the point P may also be expressed asi, mron|, The numbers Ir, mr and nr, proportional to the direction cosines are called, as direction ratios of vector , and denoted as a, b and cyrespectively., , ¥y, A, @ Note | One may note thf P +m t+r=) utfe +h°+c’ #1, ip general., Qa =

Page 4 :
“Types of Vectors, , 4}. Zero Vector, A vector whose initial and terminal points coincide, is called a zero vector, , (or null vector), and denoted as . Zero vector can not be assigned a, definite direction as it has zero magnitude OF, alternatively otherwise, it, may be regarded as having any direction., , —— apt, on, , la, , #% Unit Vector, , A vector whose magnitude is unity (i.e., 1 unit) is called a unit vector. The, unit vector in the direction of a given vector is denoted by a°7—_, , veer = Mageitue = @e

Page 5 :
~Coinitial Vectors, , Two or more vectors having the same initial point are called coinitial, , vectors. wee, ual ve A, , war, , Co u, A, gout, , af *, , “Collinear Vectors, Two or more vectors are said to be collinear if they are parallel to the, , , , same line, irrespective of their magnitudes and directions. A, ——— oe, bo, ——) t, , 0 ‘ A (pl ee, , , , —, 0 B, , vEqual Vector: ae, Two vectors(4)# bY... are said to be equal, if they have the same ~, , magnitude and direction regardless of the positions of their initial points,, , and written as ..%.=.8...... aT Te, ook (fel ePl