Page 1 :
MATHEMATICS, II PUC, VECTOR ALGEBRA, QUESTIONS & ANSWER, I, , One Mark Question, , 1) Find the unit vector in the direction of 2i + 3j + k., r, Let a = 2i + 3j + k, r, a = 2 2 + 32 + 12 =, r, rˆ a 2i + 3 j + k, \a = r =, a, 14, , 4 + 9 + 1 = 14, , r, 2, 3, 1, \aˆ =, i+, j+, k, 14, 14, 14, , r, r, r r, r r, 2) Let a = i + 2j & b = 2i + j. If a = b . Are the vectors a & b equal?, r, a = a 2 + 22 = 5,, r r, \a=b, , r, b = 22 + a 2 = 5, , But vectors are not equal since the corresponding components are distinct i.e. directions, are different., 3) Find the values of x & y so that vectors 2i+3j and xi+4j are equal., , r, r, a = 2i + 3 j, b = xi + yj, r r, Given a = b \2i + 3 j = xi + yi, \ x = 2, y = 3, , 4) Find the scalar or dot product of vectors i + 2j - 3k & 2i - j + k., (i + 2j - 3k ) . (2i - j + k ) = 1(2 ) + 2(- 1) - 3(1) = 2 - 2 - 3 = -3, , 1
Page 2 :
i- j, is a unit vector., 2, r i- j, 1, 1, a=, =, ij, 2, 2, 2, , 5) Show that, , 2, , 2, , r, 1 1, æ 1 ö æ 1 ö, a= ç, + = 1, ÷ +ç÷ =, 2 2, 2ø, è 2ø è, r, r, \ a =1, \ a is a unit vector., , II, , Two Marks Questions:, , 1) Find the vector parallel to the vector i - 2j and has magnitude 10 units., r, Let a = i - 2 j, r, 2, a = 12 + (- 2), r, \a = 5, r, rˆ a i - 2 j, \a = r =, a, 5, r, r, Let b be the vectors parallel to a having magnitude 10 units, r, \ b = 10, Q If vectors are parallel then unit, r r r, vector along & parallel vectors are, Now b = b aˆ, same, i-2j, =10 ., 5, r 10i 20 j, \Reqd vector b =, 5, 5, , r, 2) Find the direction ratios and direction cosines of the vector a = i + j - 2k ., r, a = i + j - 2k, r, 2, a = 12 + 12 + (- 2 ), r, \a = 6, r, rˆ a i + j - 2k, a= r =, a, 6, r 1, 1, 2, \aˆ =, i+, jk, 6, 6, 6, , 2
Page 3 :
r, Here direction ratios are components of a i.e.(1, 1, - 2 ), r, æ 1 1 -2, direction cosines are components of â i.e. çç, ,, ,, è 6 6 6, , ö, ÷÷, ø, , 3) Show the vectors 2i-3j+4k and -4i+6j-8k are collinear., , r, a = 2i - 3 j + 4k, r, r, b = -4i + 6 j - 8k = - 2(2i - 3 j + 4k ) = -2a, \One vector can be expressed interms of another, r r, \a & b are collinear., r r r r r, r, 4) Find x , if for a unit vector a, (x - a ) . (x + a ) = 12, r, Given a = 1, (xr - ar ) . (xr + ar ) = 12, r2 r2, x - a = 12, r2, x - 12 = 12, r2, x = 13, r, \ x = 13, r, r, r r, r, r, r r, 5) Find a - b , if two vectors a and b are such that a = 2, b = 3 and a .b = 4, r, r, r r, Given a = 2, b = 3 and a .b = 4, r r2 r2, r r r2, w.k .t. a - b = a - 2 a . b + b, , ( ), , = 2 2 - 2(4 ) + 32 = 4 - 8 + 9, r r2, a -b = 5, r r, \ a -b = 5, , 3
Page 4 :
r, r, r, r r r, 6) For any two vectors a and b prove that a · b £ a · b, r r, a .b, w.k .t. cos q = r r, a b, r r, a. b, for all values of q , - 1 £ cosq £ 1, r r = cosq, a b, \ cosq £ 1, , r r, a. b, \ r r £1, a b, r r, r r, \ a. b £ a b, , r, r, r, r r r, 7) For any two vectors a and b prove that a + b £ a + b (Triangle in equality ), r r2 r, r r r2, a + b = a 2 + 2 a. b + b, r, r r r2, rr r r, £ a 2 + 2 a. b + b, Qa.b £ a . b, r, r r r2, r r r r, £ a 2+ 2 a b + b, From previous properties a . b £ a b, r r 2, £ a+b, r r r r, \ a +b £ a + b, , ( ), , {, , }, , ( )(, )(, ), , ), , r r r r, 8) Evaluate 3a - 5b . 2a + 7b, r r, r r, r r r r, r r, r r, 3a - 5b . 2a + 7b = 6 a . a + 21 a . b - 10 b . a - 35 b . b, r, r, r r, r r, = 6a 2 + 21 a . b - 10 a . b - 35b 2, r, r, r r, = 6a 2 + 11a . b - 35b 2, r, r2, r r, = 6 a + 11a . b - 35b 2, , (, , ( ) ( ) ( ), ( ) ( ), , r, r, r r, r r, 9) If a = i - 7j + 7k & b = 3i - 2j + 2k find a ´ b and a ´ b, i, j k, r r, a´b = 1 - 7 7, 3 -2 2, = i{- 7(2) - (- 2)(7 )}- j{2 - 21} + k {- 2 + 21}, = i (- 14 + 14) - j{- 19}+ k (19), r r, \a ´ b = 19 j + 19k, , 4
Page 5 :
r, 10) Find l & m if (2i + 6j + 27k )´ (i + lj + mk ) = o, r, Given (2i + 6j + 27k )´ (i + lj + mk ) = o, i j k, r, \ 2 6 27 = o, 1 l m, , r, i(6 m - 27l ) - j (2 m - 27 ) + k (2l - 6) = o, Equating cofficient s, 6m - 27l = 0,, 2 m - 27 = 0, 2l - 6 = 0, 27, \m =, and l = 3, 2, r r, r r, r r, 11) Show that ( a - b ) ´ ( a + b ) = 2( a ´ b ), r r, r r, Consider LHS ( a - b ) ´ ( a + b ), r r r r r r r r, = a ´ a + a ´b - b ´ a - b ´b, r r r, r r r, = o + (a ´ b ) + ( a ´ b ) - o, r r, r r, r r, \ ( a - b ) ´ ( a + b ) = 2( a ´ b ), 12) Find the scalar triple product of vectors i + 2j + 3k, - i - j + k and i + j + k, 1 2 3, Scalar triple product = - 1 - 1 1, 1 1 1, = 1 (- 1 - 1) - 2 (- 1 - 1) + 3(- 1 + 1), =-2+4+0 = 2, 13) Find l if the vectors i + j + 2k, l i - j + k & 3i - 2j - k are coplanar., Given that vectors are coplanar, 1, \ l, 3, , 1, 2, -1 1 = 0, - 2 -1, , = 1(1 + 2) - 1(- l - 3) + 2(- 2l + 3) = 0, = 3 + l + 3 - 4l + 6 = 0, = -3l + 12 = 0, \l = 4, , 5
Page 6 :
III, , Three Marks Questions:, r, r r, r, 1) Consider t he points P and Q with position v ectors OP = 3a - 2b and OQ = a + b ., Find the position vector of a point R which divides line joining, the points P and Q in the ratio 2 : 1 internally and externally respectively., , Solution, , r, r, r r, given OP = 3a - 2b , OQ = a + b, , m : n = 2 :1, , Internally,, mOQ + nOP, m+n, r, r r, r, 2 a + b + 1 3a - 2b, =, 2 +1, r, r, 2a + 3a + 2b - 2b, =, 2 +1, r, 5a, OR =, 3, OR =, , (, , ) (, , ), , mOQ - nOP, m-n, r, r r, r, 2 a + b - 1 3a - 2b, =, 2 -1, r, r, 2a - 3a + 2b + 2b, =, 1, r r, OR = 4b - a, , externally OR =, , (, , ) (, , ), , 3) Find the vector joining the points P(2, 3, 0) and Q(- 1, - 2, 4) and also direction cosines of PQ, , 6
Page 8 :
5) Find the angle between the vectors i - 2j + 3k & 3i - 2j + k., r, r, Let a = i - 2j + 3k, b = 3i - 2j + k, r r, a . b = (i - 2j + 3k ) . (3i - 2j + k ) = 3 + 4 + 3 = 10, r, 2, a = 12 + (- 2 ) + 32 = 14, r, b = 32 + 22 + 12, = 14, r r, r r, a.b, 10, 10, Let q be angle between a & b then cosq = r r =, =, 14 14 14, a b, cosq =, , 5, 7, , q = cos-1, , 7, 5, , 1, (2i + 3 j + 6k ), 1 (3i - 6 j + 2k ) and 1 (6i + 2 j + 3k ), 7, 7, 7, are mutually perpendicu lar., r 1, Let a = (2i + 3 j + 6k ), 7, r 1, b = (3i - 6 j + 2k ), 7, r 1, c = (6i + 2 j + 3k ), 7, r r 1, 1, consider a . b = (2i + 3 j + 6k ) . (3i - 6 j + 2k ), 7, 7, 1, = {(2i + 3 j + 6k ) . (3i - 6 j + 2k )}, 49, 1, 1, = {6 - 18 + 12} =, {0}, 49, 49, r, r r, r, \a . b = 0, \ a is perpendicu lar to b, r r, r r, /// ly We can show that b . c = 0 & c . a = 0, rr r, \ a, b, c are mutually perpendicular vectors., 6) Show that the vectors, , 8
Page 9 :
r, r, r r r r, 7) If a = 5i - j - 3k , b = i + 3 j - 5k then show that the vectors a + b & a - b are perpendicu lar., r r, a + b = 5i - j - 3k + i + 3 j - 5k = 6i + 2 j - 8k, r r, a - b = 5i - j - 3k - (i + 3 j - 5k ) = 4i - 4 j + 2k, r r, r r, consider a + b . a - b = (6i + 2 j - 8k ). (4i - 4 j + 2k ) = 24 - 8 - 16 = 0, r r, r r, r r, r r, \ a+b . a-b =0, \ a + b is perpendicu lar to a - b, , (, , ) (, ) ( ), , (, , ), , r, r, r, r, r, 8) If a = 2i + 2 j + 3k , b = -i + 2 j + k and c = 3i + j and such that a + lb is, r, perpendicu lar to c then find l ., r, r, a + lb = 2i + 2 j + 3k + l (- i + 2 j + k ), r, r, \ a + lb = (2 - l )i + (2 + 2l ) j + (3 + l )k, r, r, r, Given a + lb is ^ r c., r r, r, a + lb . c = 0, {(2 - l )i + (2 + 2l ) j + (3 + l )k } . {3i + j} = 0, 6 - 3l + 2 + 2l = 0 Þ -l + 8 = 0, \l = 8, , (, , ), , r r r, r r r r, r r rr r r, 9) If a , b , c are unit vectors such that a + b + c = o then find a . b + b . c + c . a, r, r, r, a = 1, b = 1, c = 1, r r r r rr, a . a + b + c = a. o, r r r r r, a 2 + a .b + a . c = 0, r r rr, r, a . b + a .c = - a 2, r r r r, r, /// ly b . c + c . a = -b 2, r r r r, r, c . a + a . b = -c 2, rr rr rr, r r r, Adding 2 a.b + b .c + c .a = - a 2 - b 2 - c 2 = -12 - 12 - 12, r r r r r r, 2 a . b + b . c + c . a = -3, rr rr rr, Q a.b + b .c + c .a = - 3 2, , (, , (, , ), , (, , ), , ), , 9
Page 10 :
r r, r r, 10) Find a vector and unit vector perpendicu lar to each of the vector a + b and a - b, r, r, where a = 3i + 2j + 2k & b = i + 2j - 2k, r r, a + b = 3i + 2j + 2k + i + 2j - 2k, r r, \ a + b = 4i + 4 j, r r, a - b = 3i + 2j + 2k - i - 2j + 2k, r r, \ a - b = 2i + 4k, , (, , ) (, , ), , (, , ) (, , r, r r, r r, r r r r r, Let c be the vector perpendicu lar to a + b and a - b then c = a + b ´ a - b, + - +, i j k, r, c = 4 4 0 = i (16 - 0 ) - j (16 - 0 ) + k (0 - 8), 2 0 4, r, \ c = 16i - 16 j - 8k, r, 2, c = 16 2 + 16 2 + (- 8) = 256 + 256 + 64 = 576 = 24, r, r r, r r, Let ĉ be the unit vector perpendicu lar to a + b and a - b, r, r c, then ĉ = r, c, , (, , ), , r 16i -16j - 8k 2i 2 j k, ĉ =, = 3 3 3, 24, , 10, , )
Page 11 :
r, 11) If a unit vector a makes angles p 3 with i, p 4 with j and and acute angle, r, q with k then find q and hence components of a., r, Let a , b , g be the angles made by a with i, j, k then, a = p 3 , b = p 4, g = q, r, Let a = a1i + a2 j + a3k, r, Given a = 1, then cosa =, , a1, a1, , cos p 3 =, , a1, 1, , \a1 = 1 2, a, cos b = r2, a, cos p 4 =, \a2 = 1, , a2, 1, 2, , a, cos g = r3, a, cosq = a3, a3 = cosq, r 1, 1, \a = i +, j + cosq k, 2, 2, 2, , 2, , r, æ1ö æ 1 ö, 2, a = ç ÷ +ç, ÷ + (cosq ), è2ø è 2 ø, 1 1, + + cos 2 q, 4 2, 3, \1 = + cos 2 q, 4, 2, cos q = 1 4, cosq = ± 1 2, 1=, , q = 600 or 1200, r 1, 1, 1, \a = i +, j+ k, 2, 2, 2, , or, , r 1, 1, 1, a = i+, j- k, 2, 2, 2, , 11
Page 12 :
12) Find the area of triangle with vertices A(1, 1, 2), B(2, 3, 5), C (1, 5, 5), A º (1, 1, 2), , OA = i + j + 2k, , B º (2, 3, 5), , OB = 2i + 3 j + 5k, , C º (1, 5, 5), , OC = i + 5 j + 5k, , AB = OB - OA, = 2i + 3 j + 5k - i - j - 2k, AB = i + 2 j + 3k, AC = OC - OA, = i + 5 j + 5k - i - j - 2k, AC = 4 j + 3k, i j k, AB ´ AC = 1 2 3, 0 4 3, = i(6 - 12 ) - j (3 - 0) + k (4 - 0) = -6i - 3 j + 4k, AB ´ AC =, , (- 6 )2 + (- 3)2 + 4 2, , Area of triangle ABC =, , = 36 + 9 + 16 = 51, , 1, 1, AB ´ AC =, 51 sq units, 2, 2, , 12
Page 13 :
13) Find the area of parallelog ram whose adjecent sides are 2i - 4j + 5k and, i - 2j - 3k. Also find unit vector parallel to its diagonal., r, r, a = 2i - 4j + 5k, b = i - 2j - 3k, i, j, r r, a´b = 2 -4, , k, , 5 = i{12 + 10} - j{- 6 - 5}+ k {- 4 + 4 } = 22i + 11 j, , 1 -2 -3, r r, a´b =, , (22)2 + (11)2 + 0 =, , 242 + 121 + 0 = 363, r r, Area of parallelog ram ABCD = a ´ b = 363 sq.units, r r, Diagonal AC = a + b, = 2i - 4j + 5k + i - 2j - 3k, AC = 3i - 6 j + 2k, AC = 32 + (- 6 ) + 2 2 = 9 + 36 + 4 = 49 = 7, 2, , ^, , Unit vector along AC,, , AC =, , AC, AC, , =, , 3i - 6 j + 2k, 7, , Unit vector parallel to AC = Unit vector along AC =, , 3i - 6 j + 2k, 7, , r, r, 14) Show that the points A, B, C with position v ectors a = 3i - 4j - 4k, b = 2i - j + k, r, & c = i - 3j - 5k respectively form the vertices of a right angled triangle., Given A º (3, - 4, - 4) B º (2, - 1,1), , C º (1, - 3, - 5), , Given OA = 3i - 4 j - 4k, , 13
Page 14 :
OB = 2i - j + k, OC = i - 3 j - 5k, AB = OB - OA, = 2i - j + k - 3i + 4 j + 4k, \ AB = -i + 3 j + 5k, BC = OC - OB, = i - 3 j - 5k - 2i + j - k, \BC = -i - 2 j - 6k, CA = OA - OC, = 3i - 4 j - 4k - i + 3 j + 5k = 2i - j + k, AB + BC + CA = -i + 3 j + 5k - i - 2 j - 6k + 2i - j + k, r, \ AB + BC + CA = O, \Dle law is satisfied, r r r, \ a , b , c form a Dle, AB =, , (- 1)2 + 32 + 5 2, , BC =, , (- 1)2 + (2)2 + 6 2, , = 35, = 41, , 2, , AB = 35, 2, , BC = 41, , CA = 2 2 + (- 1) + (- 1) = 6, 2, , 2, , We can see that AB + AC, 2, , \ AB + AC, , 2, , 2, , CA = 6, , 2, , 2, , = BC, , = 35 + 6 = 41 = BC, 2, , \Pythagrous theorem is satified., r r r, i.e. a, b, c form a right angled triangle, , 14, , 2
Page 15 :
[, ] [ ], ) {( ), }, ){, }, ){, }, ) ( ), ( ) (, ), ) ( ) ( ) [ ], , r r r r r r, rrr, 14 ) Prove that a + b , b + c , c + a = 2 a b c, r r, r r, r r, LHS = a + b . b + c ´ (c + a ), r r r r r r r r r r, = a + b . b´c + b´a +c´c + c´a, r r r r r r r r, = a + b . b´c- a´b+ c´a, r r r, r r r, r r r, r r r, r r r, r r r, = a . b ´ c - a . a ´ b + a .(c ´ a ) + b b ´ c - b a ´ b + b .(c ´ a ), r r r, r r r, = a . b ´ c - 0 + 0 + 0 - 0 + b .(c ´ a ), r r r, r r r, r r r, r r r, = a. b ´ c + a b ´ c = 2a. b ´ c = 2 a , b , c, , (, (, (, , (, (, (, , ), , 14) Show that the vectors 4i - j + k, 3i - 2j - k and i + j + 2k are coplanar, r, Let a = 4i - j + k, r, b = 3i - 2j - k, r, c = i + j + 2k, 4 -1 1, r r r, consider a. b ´ c = 3 - 2 - 1, , (, , ), , 1, , 1, , 2, , = 4{- 4 + 1} + 1{ 6 + 1 }+ 1{3 + 2}, = -12 + 7 + 5, r, r, r, \a. b ´ c = 0, \vectors are coplanar, , (, , ), , Scalar Triple Product of vectors, , (, , ) (, , ), , r r r, r r r, r r r, If a, b, c are non zero vectors then a. b ´ c or a ´ b .c, is called scalar triple product of vectors., r r r, r r r, r r r, The scalar triple product of a, b, c is denoted by a b c or a, b, c, , [, , a1, r r r, Then a. b ´ c = b1, c1, , (, , ), , a2, b2, c2, , ] [, , a3, b3, c3, , since scalar triple product is a determinen t , all determinen t, properties are satisfied., Properties, 15, , ]
Page 16 :
( ), ( ), [ ][ ] [, ( ), [ ], ( ) (, [ ] [ ], , r r r, 1) a. b ´ c is a scalar., r r r r r r r r r, 2) a. b ´ c = b.(c ´ a ) = c . a ´ b, rrr r r r, rrr, abc = b c a = c ab, r r r, r r r, 3) a. a ´ b = 0 ,, a. b ´ b = 0, rr r, r r r, aa b = 0, a b b =0, r r r, r r r, 4 ) a. b ´ c = - a . c ´ b, rrr, rr r, a b c = - a c b etc., 5) Dot and cross can be interchanged, r r r, r r r, a. b ´ c = a ´ b . c, r r r r r r, b ´ c . a = b . (c . a ) etc., , (, , (, , ), , ) (, , (, [, ), , (, ], , ), , ), , ], , ), , Coplanar vector:, The vectors are said to be coplanar if they lie on same plane, or parallel planes., , ( ), , r r r, The condition for the vectors to be coplanar is a. b ´ c = 0, , Problems:, , 1) Find the scalar triple product of vectors i + 2j + 3k, - i - j + k and i + j + k, 1 2 3, Scalar triple product = - 1 - 1 1, 1, , 1, , 1, , = 1 (- 1 - 1) - 2 (- 1 - 1) + 3(- 1 + 1), =- 2+ 4+0 = 2, 16
Page 17 :
[, , ] [ ], , r r r r r r, rrr, 2) Prove that a + b, b + c, c + a = 2 a b c, , ( ) {( ), }, ( ){, }, ( ){, }, ( ) ( ), ( ) ( ), ( ), ( ) ( ) ( ) [ ], , r r r r, r r, LHS = a + b . b + c ´ (c + a ), r r r r r r r r r r, = a + b . b´ c + b´a + c ´ c + c ´a, r r r r r r r r, = a + b . b´ c - a ´ b + c´a, r r r r r r r r r rr r rr r r r r, = a. b ´ c - a. a ´ b + a.(c ´ a ) + b b ´ c - b a ´ b + b.(c ´ a ), r r r, r r r, = a. b ´ c - 0 + 0 + 0 - 0 + b.(c ´ a ), r r r rr r, r r r, r r r, = a. b ´ c + a b ´ c = 2a. b ´ c = 2 a, b , c, , 3 ) Show that the vectors 4i - j + k, 3i - 2j - k, and i + j + 2k are coplanar, r, Let, a = 4i - j + k, r, b = 3i - 2j - k, r, c = i + j + 2k, 4, r, r, r, consider a . b ´ c = 3, , (, , ), , -1, -2, , 1, -1, , 1, , 2, , 1, , (, , ), , = 4{- 4 + 1} + 1{ 6 + 1 }+ 1{3 + 2}, = - 12 + 7 + 5, , r r r, \ a. b ´ c = 0, \ vectors are coplanar, , 4 ) Find l if the vectors i + j + 2k, l i - j + k & 3i - 2j - k are coplanar., 17
Page 18 :
Given that vectors are coplanar, 1, \ l, , 1, , 2, , -1, , 1 =0, , 3 - 2 -1, = 1(1 + 2 ) - 1(- l - 3) + 2(- 2l + 3) = 0, = 3 + l + 3 - 4l + 6 = 0, = -3l + 12 = 0, \l = 4, , 18
 Learn better on this topic
Learn better on this topic



















































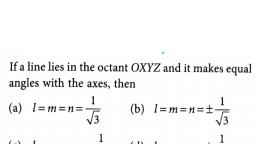













 Learn better on this topic
Learn better on this topic









