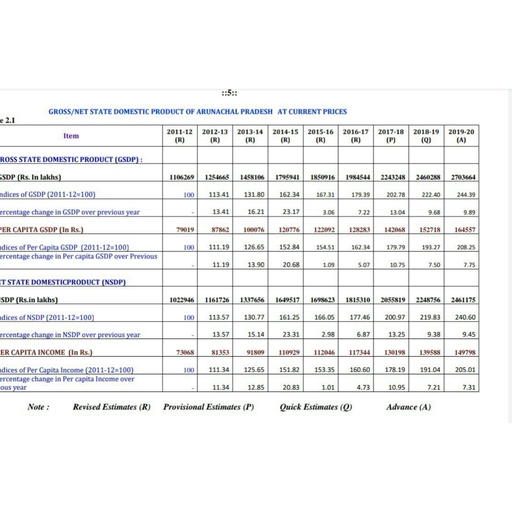
Page 1 :
The returns to factor or the law of variable, proportions, discussed in the preceding chapter,, signified the short run production function with one, variable factor, when other factors were supposed, to be constant. In the present chapter, we shall, consider the production function involving two factor, inputs, say labour and capital, which are both the, variable factors. Analysis of such a production, function is based upon the fundamental concept of, isoquants or equal product curves., , 14.1 ISOQUANT, , The term ‘isoquant’ is made up of two words, ‘iso’ and ‘quant’. ‘Iso’ means ‘equal’ and ‘quant’, means ‘quantity’. The isoquant thus, is a curve which, represents such combinations of two variable factor, inputs that yield equal output. In other words,, Isoquant can be defined as the locus of all such, combinations of the two variable factor inputs (say, labour and capital) that are capable of producing, the same level of output. The isoquants or equal, product curves are analogus to the indifference, curves employed in the theory of consumer, behaviour, They differ from consumer indifference, curves in two respects. Firstly, the indifference curve, represents combinations of two commodities that, provide equal satisfaction to the consumer, whereas, isoquant or equal product curve represents such, combinations of two factor inputs that yield the same, level of output of a commodity. Secondly, indifference, curve is connected with same satisfaction or utility, which is non-measurable. The equal product curve,, on the other hand, is connected with the product, quantity which is exactly measurable and remains, exactly equal in case of all the factor combinations,, Still isoquants have so close similarity with consumer, indifference curves that these are often termed also, , as production indifference curves., , Theory of Production—, Two Variable Factor Inputs, , , , Assumptions : The device of isoquants or equal, product curve rests on the following assumptions :, , (i) Production of the commodity X involves, only two factor inputs—labour (L) and capital (K)., (ii) The units of each factor input are, homogeneous., (iii) The two inputs are substitutable., (iv) The production techniques remain fixed., (v) The two factor inputs are perfectly divisible., , The equal product combinations of the variable, factor inputs, labour and capital, are shown in the, hypothetical Table 14.1 given below :, , Table 14.1, Equal Product Combinations of, Labour and Capital, , , , , , , , Combinations] Units of Units of Level of, Labour (L) | Capital (K) | Output of X, A 1 24 100, B 2 16 100, c 3 10 100, D 4 6 100, E 5 100, , , , , , , , , , , , In Table 14.1, combinations A,B,C,D and E of, two factor inputs, labour (L) and capital (K) yield the, same level of output (100 units) of X-commodity. In, combination A, | unit of labour and 24 units of capital, produce 100 units of commodity X. In combination, B, units of labour are increased to 2 and at the same, time units of capital are reduced to 16 and production, still remains 100 units of X, Similarly in combination, C, 3 units of labour and 10 units of capital, in, combination D, 4 units of labour and 6 units of capital, and in combination E,5 units of labour and 4 units, of capital, all turn out 100 units of X commodity. If, all these combinations yielding equal output are, , 254

Page 2 :
<a, , we, , , , THEORY OF PRODUCTION, , denoted through a curve, such a curve is called as, gn isoquant or equal product curve, which is shown, , through Fig.14.1., Y, , , , , , , , Labour, Fig.14.1, , In Fig 14.1, labour is measured along the, horizontal scale and capital along the vertical scale., Given the combinations A,B,C,D and E, according to, Table 14.1, the points A,B,C,D and E are shown in, Fig.14.1. By joining these points, the isoquant Q(100), has been drawn. It signifies that all these, combinations of labour and capital yield an equal, output 100 units of X commodity. In the different, factor combinations, while the input of labour is, increased that of capital is reduced so that output, remains unchanged. Consequently, the isoquant, slopes downwards from left to right., , 14.2 MAP OF ISOQUANTS, , If the producer wants to secure a level of output, more than 100 units of X commodity, the same, quantities of labour and capital can not assure that, higher level of output. The producer will have to, raise the input of labour or capital or both to do so., It means such combinations cannot lie on the same, isoquant but upon some higher isoquant. Similarly,, the factor combinations consisting of reduced, quantities of labour or capital or both than before, would be associated with a lower level of output of, X than 100 units. Such combinations will lie upon a, lower isoquant. Thus there can be a series of, isoquants or equal product curves representing, different levels of output. Such a series of isoquants, can be called as a map of isoquants. Thus the map, of isoquants represents a series of isoquants, indicating different levels of output from the different, factor combinations. Higher the isoquant, higher is, the level of output and vice-versa., , 255, , The map of isoquants or equal product curves, is shown through Fig. 14.2., , vy:, , Capital, is, , AR, , , , , , Q (200), Q (150), , H Q (100), Sea x, Labour, , Fig. 14.2, , In Fig 14.2, the isoquants Q (100), Q (150) and, Q(200) are shown. They represent the map of, isoquants. The line OR is passed through this map., The combination F, employing OL units of labour and, OK units of capital, can produce 100 units of X, commodity and it lies upon the lowest isoquant, Q (100). The combination G employs more units of, labour OL, and more units of capital OK). It can, produce 150 units of X and it lies upon the higher, isoquant Q (150). The combination H includes still, more units of labour OL, and more units of capital, OK. It can produce still larger quantity 200 units of, X commodity and it lies upon the highest isoquant, , Q (200)., , 14.3 MARGINAL RATE OF TECHNICAL, SUBSTITUTION, , Since all the factor combinations lying upon a, given isoquant yield the same level of output, it, means the gain in output due to increase in the input, of labour is fully offset by the loss of output due to, the reduction in the input capital. In other words,, the producer substitutes some quantity of labour, input for some quantity of the other input capital., The rate at which one factor input is substituted for, the other, keeping the level of output unchanged,, is termed as the marginal rate of technical, substitution (MRTS). The marginal rate of technical, subtilution of labour for capital (MRTS ,,) can be, , defined also as a ratio of change in capital to a change, in labour input., , , , MRTS | = Changein CapitalInput _ 5K, Change in Labour Input ~ 8L

Page 3 :
256, , It may be amplified through the Table 14.2 given, below :, , Table 14.2, Marginal Rate of Technical Substitution, of Labour for Capital, , , , , , , , , , Combinations] Units of Units of | MRTS,x, Labour (L)} Capital (Kk), A 1 24 =, B 2 16 8:1, Cc 3 10 6:1, D 4 6 4:1, E 5 4 2:1, , , , , , , , , , , , In combination A, producer employs 24 units of, capital and 1 unit of labour. In combination B, the, same level of output is maintained by employing 2, units of labour and 16 units of capital, Producer, increases the input of labour by one unit but, at the, same time, reduces the input of capital by 8 units. In, other words, he substitutes one unit of labour in, place of 8 units of capital, so that MRTS,, is, — SK/6L = 8/1 or 8 : 1. In the case of combination iC, producer employs 3 units of labour along with 10, units of capital and still secures the same level of, output. Thus in this case, he substitutes one more, unit of labour in place of 6 units of capital. The, MRTSyx, in this case is -8K/5L = 6/1 or 6: 1. The, MRTS,x can be measured with the help of the, Fig. 14.3., , Y/, , Capital, , , , , , cf: {scale x, Labour, Fig. 14.3, , In Fig. 14,3. Given the isoquant Q, in combination, A, producer employs OL units of labour and OK units, of capital. In combination B, he increases the input, of labour by LL, or 1 unit of labour and , at the same, time, gives up KK, units of capital., , -KK, _-8K, , ih vO, , MRTSy atA = =Tan o, , MICRO-ECONOMIC THEORY, , As the producer increases the input of labour, again by | unit or L,Lp, the input of capital is reduced, by KiK,, , -K,Ky Tank, LiL, 6L, , MRTS of labour for capital measures the stope, of the isoquant. Since MRTS;x is negative, it means, the isoquant slopes downwards from left to right, , Since all the combinations of factors on a given, isoquant yield the same level of output, it therefore, follows that, , Loss in output due to Gain in output due to, reduction in the input = increase in the input _, , , , , MRTS,x at B=, , of capital of labour, —5K x MPPx = 5L * MPP,, OK MER:, Zou) MPPx, = 36K = MPR., MENS ae MPP,, , ‘Thus the MRTS;x can also be defined as the, ratio of MPP, to MPP,., , Diminishing Marginal Rate of Technical, Substitution, , As the producer increases the input of labour, relative to that of capital, there is a fall in the marginal, physical product of labour and a rise in the marginal, physical product of capital on account of the principle, , MPP,, : ce MPP, ”, , fall in MPP, and a rise in MPP,, leads to decrease in, the MRTS,x with an increase in the input of labour., According to Table 14.2. as the input of labour is, increased, the rate of substitution of labour for capital, goes on diminishing, Initially, in the combination 1B:, the MRTS; x is 8: 1; and finally in the combination, E, it decreases to just 2 : 1. According to Fig. 14.3,, , the diminishing marginal rate of technical substitution, of labour for capital is explicit., , of diminishing returns. Since MRTS; x =, , , , KK,, MRTS,x atA= ——1, LK LL, Tana, , and MRTS;x at B= S!K2 _ tang, UL,

Page 4 :
THEORY OF PRODUCTION, , , , , , Since KK, < KK, and LL, = LL) = one unit of, Jabour, therefore Tan 8 < Tan a . It implies that, MRTS)x at B is less than MRTS,, at A. Hence with, an increase in the input of labour, the isoquant is a, convex curve to the origin. If the MRTS;, were, constant, the isoquant would have been a negatively, sloping straight line. In case the MRTS;, were, increasing, the isoquant would have been a negatively, sloping concave curve to the origin. The last two, possibilities do not exist in actual life. Hence the, isoquant can only be a negatively sloping convex, curve to the origin., , 14.4 PROPERTIES OF ISOQUANTS OR, EQUAL PRODUCT CURVES, , The isoquants or equal product curves have the, properties similar to those of indifference curves of, a consumer, The main properties of isoquants are as, under., , (® The isoquants slope negatively or slope, downwards from left to right : An isoquant slopes, negatively or slopes downwards from left to right., The producer increases the input of one factor and, at the same time reduces the input of other factor, (see Fig 14.1). It is only in such a unique situation, that output of commodity can remain unchanged. In, any other alternative shape of isoquant, all, combinations lying upon a given isoquant can not, yield equal quantity of the product., , (i) The isoquants are convex to the origin :, Since with an increase in the input of one factor, (labour), its manginal rate of technical substitution, for the other factor (capital) diminishes (see Fig. 14.3),, it means slope of isoquant decreases as the input, of labour is increased and the isoquant can only be, a negatively sloping convex curve to the origin., , (iii) Higher the isoquant, higher is the level of, output and vice-versa : Like consumer’s indifference, map, there is a map of isoquants. Higher the isoquant,, higher is the level of output and vice-versa. (See, Fiz.14.2)., , (iv) Two isoquants cannot cut each other : Two, isoquants can neither touch each other nor can they, intersect each other. In order to prove it, let us, Suppose that two isoquants Q, and Q, cut each other, at R, as shown in Fig. 14.4., , The combinations R and S lie on the same, isoquant Q,, ; R= 5 (i), , , , 257, V4, g, sos, OO, o R, T, ‘Qz (200), Ss, Q, (100), 0 Labour, Fig. 14.4, , The combinations R and T lie on the same, isoquant Q), 2 Ree, From (i) and (ii), Sime, But this is impossible because combination T, lies on the higher isoquant Q, yielding a higher, output of 200 units, whereas combination S lies on, a lower isoquant Q, yielding an output of 100 units., , , Our supposition is wrong., , (ii), , Hence two isoquants cannot cut each other., , (v) Shape of isoquants in case of perfect, substitutes and perfect complementary factors :, Normally an isoquant is a negatively sloping convex, curve to the origin. But there are two exceptional, cases, when factors are perfect substitutes and, perfect complements. The two factor inputs are, supposed to be perfect substitutes, when each one, of them can be used equally well for the other. The, MRTS between such factors remains constant., Practically, the two factors can be regarded as single, homogeneous factor. Since in case of perfect, substitutes, MRTS remains throughout unchanged,, the isoquant related to them will be a negatively, sloping straight line. The perfect substitutability is, a rare phenomenon in actual life., , The factors are said to be perfect complements,, when these are employed in a fixed proportion., , Suppose 2 units of labour and 3 units of capital are, , combined to produce 50 units of X commodity and, 4 units of labour and 6 units of capital are combined, to produce 100 units of X. Since the two factors are, being used in a fixed proportion at varying levels of, output, these will be regarded as perfect

Page 5 :
MICRO-ECONOMIC THEORY, , secured from alternative production processes. In, case of each one of the production process, there is, different proportion in which the two factors are, combined. There is a fixed factor proportion in each, production process. But these fixed factor, proportions are not equal in all the Production, processes. The linear programming isoquant or, kinked isoquant can be drawn as shown through, Fig, 14.7., , Hy, , , , , Capital, , Q, (100), , Q, (100), Q (100), , , , o Labour X, Fig. 14.7, , In Fig. 14.7, the production processes A, B and, C have fixed factor proportions of labour and capital., Their respective fixed capital-labour ratios are, measured by the slopes of the process rays OA, OB, and OC. Q, Q, and Q, are the fixed proportion rightangled isoquants. Each represents the same level of, output of 100 units of X. By joining the points A, B,, and C, the isoquant can be drawn. It is like the, smoothed isoquant but the essential difference is that, A, B and C alone are the technically feasible factor, combinations yielding an output of 100 units of X., The points in between A, B and C are not relevant., Such a linear programming isoquant has kinks in it, at the points A, B and C. That is why, it is also, termed as a kinked isoquant., , as ee ee i AT, , 14.6 ISO-COST LINE, , The iso-cost line indicates the different, combinations of two factors (labour and capital), which a firm can actually buy, given the total outlay, and prices of the two factors. In other words, the, iso-cost line shows such factor combinations which, involve equal cost or outlay. It is also called as the, tt factor-price line or factor-outlay line. Suppose price, , of labour is Rs. 8 per labour-hour and that of capital, is Rs. 10 per machine-hour, If the total outlay or, amount available for spending is Rs. 800, the, producer can buy 100 units of labour + 0 unit of, , eee oe Ne, , a, , , , THEORY OF PRODUCTION, , capital, ifthe whole amount is spent on labour alone., He can buy 9 unit of labour + 80 units of capital, if, the whole amount is spent on capital alone. In, between these two extreme combinations, there can, be several other combinations which the firm can, actually buy, such as 25 units of labour + 60 units, of capital, 50 units of labour + 40 units of capital ete., The iso-cost line is the locus of all the factor, combinations which the producers can employ, given, the total outlay and prices of the two factors. The, iso-cost line is shown though Fig. 14.8., , B, , OMEEsnison Ge 80 100°, Labour, , Fig. 14.8, , In Fig. 14.8, AB is the iso-cost line. All, combinations of labour and capital, given the total, ‘outlay of Rs 800 and prices of labour and capital as, Rs 8 and Rs 10 per unit respectively, that the producer, can procure, lie upon the line AB. The slope of the, isocost line is ratio of the price of labour (P;) to, the price of capital (Px)., , It can be derived as follows :, , ; OA, Slope of Iso-cost line AB = OB, TotalOutlay __ Total Outlay, , IS Price of Capital Pe, TotalOutlay __ Total Outlay, OB* Price of Labour PL, , Slope of Iso-cost Line, OA _ TotalOutlay _ Total Outlay, , BUST op oT Pe a, MotalOutlay. Eis Eu., = Px TotalOutlay Px, , If P,= w (wage rate) and Px=r (rate of interest),