Page 1 :
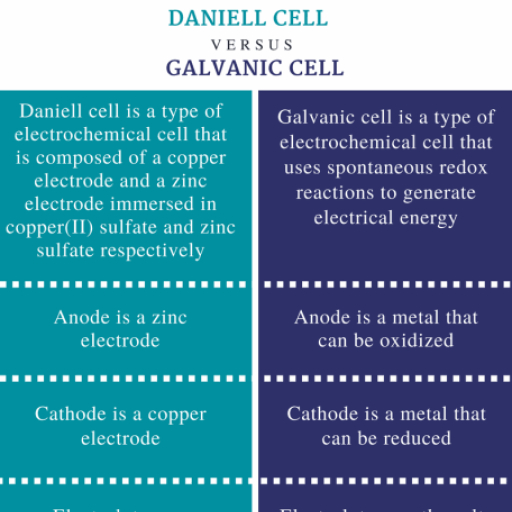
ELECTROCHEMISTRY, , ELECTROCHEMISTRY, , 1., , ELECTROCHEMISTRY, Electrochemistry is the study of production of electricity, from the energy released during a spontaneous chemical, reaction and the use of electrical energy to bring about, non-spontaneous chemical transformations., , 2., , 5., , 5.1, , Galvanic Cells, Converts chemical energy into electrical energy, , 3.2, , ELECTRODE POTENTIAL, It may be defined as the tendency of an element, when it is, placed in contact with its own ions to either lose or gain, electrons and in turn become positively or negatively charged., , Electrochemical Cells are of two types:, 3.1, , Preferential Discharge of ions, Where there are more than one cation or anion the process, of discharge becomes competitive in nature. Discharge, of any ion requires energy and in case of several ions, being present the discharge of that ion will take place first, which requires the energy., , 6., , TYPES, , ELECTROLYTIC CELL, These electrodes are dipped in and electrolytic solution, containing cations and anions. On supplying current the, ions move towards electrodes of opposite polarity and, simultaneous reduction and oxidation takes place., , ELECTROCHEMICAL CELLS, A spontaneous chemical process is the one which can, take place on its own and in such a process the Gibb’s, energy of the system decreases. It is this energy that, gets converted to electrical energy.The reverse process, is also possible in which we can make non-spontaneous, processes occur by supplying external energy in the form, of electrical energy. These inter conversions are carried, out in equipments called Electrochemical Cells., , 3., , the external circuit. Anode is assigned negative polarity, and cathode is assigned positive polarity. In Daniell Cell,, Zn acts as the anode and Cu acts as the cathode., , The electrode potential will be named as oxidation or, reduction potential depending upon whether oxidation or, reduction has taken place., , Electrolytic Cells, Converts electrical energy into chemical energy., , 4., , oxidation, ZZZZZ, X M n  aq  ne , M s YZZZZ, reduction Z, , GALVANIC CELL, , reduction, ZZZZZ, X, M n  aq  ne  YZZZZ, ZM s, oxidation, , Cell energy is extracted from a spontaneous chemical, process or reaction and it is converted to electric current., For example, Daniell Cell is a Galvanic Cell in which Zinc, and Copper are used for the redox reaction to take place., Zn (s) + Cu2+ (aq), , 6.1, , (a) Both oxidation and reduction potentials are equal in, magnitude but opposite in sign., , Zn2+ (aq) + Cu(s), , Oxidation Half : Zn (s), , (b) It is not a thermodynamic property, so values of E are, not additive., , Zn2+ (aq) + 2e–, , Reduction Half : Cu2+(aq) + 2e–, , Characteristics, , Cu(s), 2+, , Zn is the reducing agent and Cu is the oxidising, agent.The half cells are also known as Electrodes. The, oxidation half is known as Anode and the reduction half is, called Cathode. Electrons flow from anode to cathode in, , 7., , STANDARD ELECTRODE POTENTIAL (EO), It may be defined as the electrode potential of an electrode, determined relative to standard hydrogen electrode under, standard conditions. The standard conditions taken are :

Page 2 :
ELECTROCHEMISTRY, (i) 1M concentration of each ion in the solution., , Zn(s) | Zn2+ (1 M) || Cu2+ (1 M) | Cu EMF = +1.1V, , (ii) A temperature of 298 K., , (f) If an inert electrode like platinum is involved in the, construction of the cell, it may be written along with the, working electrode in bracket say for example, when a zinc, anode is connected to a hydrogen electrode., , (iii) 1 bar pressure for each gas., , 8. ELECTROCHEMICAL SERIES, The half cell potential values are standard values and are, represented as the standard reduction potential values, as shown in the table at the end which is also called, Electrochemical Series., , 9., , CELL POTENTIAL OR EMF OF A CELL, The difference between the electrode potentials of two, half cells is called cell potential. It is known as electromotive, force (EMF) of the cell if no current is drawn from the cell., , Zn s | Zn 2 C1 || H  C2 | H 2 | Pt s, , 11. SALT BRIDGE, Salt bridge is used to maintain the charge balance and to, complete the circuit by facilitating the flow of ions through it., It contains a gel in which an inert electrolyte like Na2SO4 or, KNO3 etc are mixed. Negative ions flow to the anode and, positive ions flow to the cathode through the salt bridge and, charge balance is maintained and cell keeps on functioning., , Ecell = Ecathode + Eanode, For this equation we take oxidation potential of anode and, reduction potential of cathode., Since anode is put on left and cathode on right, it follows, therefore,, = ER + EL, For a Daniel cell, therefore, E ocell, , E oCu 2 / Cu  EoZn / Zn 2, , 0.34  0.76, , 1.10 V, , 10. CELL DIAGRAM OR REPRESENTATION, OF A CELL, The following conventions or notations are applied for writing, the cell diagram in accordance with IUPAC recommendations., The Daniel cell is represented as follows :, 2+, , 2+, , Zn(s) | Zn (C1) || Cu (C2) | Cu (s), (a) Anode half cell is written on the left hand side while, cathode half cell on right hand side., (b) A single vertical line separates the metal from aqueous, solution of its own ions., Zn s | Zn, , 2, , Anodic chamber, , aq ;, , Cu, , 2, , 12. SPONTANEITY OF A REACTION, 'G = – nFECELL, For a spontaneous cell reaction ΔG should be negative, and cell potential should be positive., If we take standard value of cell potential in the above, equation we will obtain standard value of ΔG as well., ΔGo = – nFE0CELL, , aq | Cu s, , Cathodic chamber, , 13. TYPES OF ELECTRODES, (c) A double vertical line represents salt bridge, 13.1 Metal-Metal Ion electrodes, (d) The molar concentration (C) is placed in brackets after, the formula of the corresponding ion., (e) The value of e.m.f. of the cell is written on the extreme, right of the cell. For example,, , A metal rod/plate is dipped in an electrolyte solution, containing metal ions. There is a potential difference, between these two phases and this electrode can act as a, cathode or anode both.

Page 3 :
ELECTROCHEMISTRY, , Anode: M, , Mn+ + ne–, , Cathode: Mn+ + ne–, , M, , 13.2 Gas Electrodes, Electrode gases like H2, Cl2 etc are used with their respective, ions. For example, H2 gas is used with a dilute solution of HCl, (H+ ions). The metal should be inert so that it does not react, with the acid., , Cathode :, 2Hg(l) + 2Cl–(aq), , Hg2Cl2(s) + 2e–, Anode :, 2Hg(l) + 2Cl–(aq), , Anode: H2, , Hg2Cl2(s) + 2e–, , This electrode is also used as another standard to measure, other potentials. Its standard form is also called Standard, Calomel Electrode (SCE)., , 2H+ + 2e–, , 13.5 Redox Electrode, , Cathode: 2H+ + 2e–, , H2, , The hydrogen electrode is also used as the standard to, measure other electrode potentials. Its own potential is, set to 0 V as a reference. When it is used as a reference, the concentration of dil HCl is taken as 1 M and the, electrode is called “Standard Hydrogen Electrode (SHE)”., 13.3 Metal-Insoluble salt electrode, We use salts of some metals which are sparingly soluble, with the metal itself as electrodes. For example, if we use, AgCl with Ag there is a potential gap between these two, phases which can be identified in the following reaction:, AgCl(s) + e–, , Ag(s) + Cl–, , This electrode is made by dipping a silver rod in a solution, containing AgCl(s) and Cl– ions., 13.4 Calomel Electrode, Mercury is used with two other phases, one is a calomel, paste (Hg2Cl2) and electrolyte containing Cl– ions., , In these electrodes two different oxidation states of the, same metal are used in the same half cell. For example,, Fe2+ and Fe3+ are dissolved in the same container and an, inert electrode of platinum is used for the electron transfer., Following reactions can take place:, Fe3+ + e–, Anode: Fe2+, Cathode: Fe3+ + e–, , Fe2+, , 14. NERNST EQUATION, It relates electrode potential with the concentration of ions., Thus, the reduction potential increases with the increase, in the concentration of ions. For a general electrochemical, reaction of the type., , , ne, aA  bB o, cC  dD, , Nernst equation can be given as, , E cell, , E, , o, cell, , C, RT, , ln, nF, A, , c, a, , D, B, , d, b

Page 4 :
ELECTROCHEMISTRY, , E cell, , E, , o, cell, , c, , C, 2303, , RT log, nF, A, , a, , d, , D, B, , b, , Substituting the values of R and F we get, , concentrations and the solutions are connected through, salt bridge, such cells are known as concentration cells., For example, H2 | H+(c1) || H+ (c2) | H2, Cu | Cu+2 (c1) || Cu2+(c2) | Cu, , E cell, , E ocell , , C, 0.0591, log, n, A, , c, , D, , a, , B, , d, b, , ,at 298 K, , 15. APPLICATIONS OF NERNST EQUATION, , These are of two types :, 16.1 Electrode concentration cells, H2 (P1) | H+ (C) || H+ (C) | H2(P2), , 15.1 Equilibrium Constant from Nernst Equation, For a Daniel cell, at equilibrium, , E cell, , or, , E, , o, cell, , 0, , E ocell , , ª Zn 2  º, 2.303 RT, log ¬ 2  ¼, 2F, ¬ªCu º¼, , ª Zn 2  º, 2.303RT, log ¬ 2  ¼, 2F, ¬ªCu º¼, , Ecell = 0 –, , where p 2  p1 for spontaneous reaction, 16.2 Electrolyte concentration cell, The EMF of concentration cell at 298 K is given by, Zn | Zn2+ (c1) || Zn2+ (c2) | Zn, E cell, , ª¬ Zn 2  ¼º, But at equilibrium, ª 2  º, ¬ Cu ¼, , Kc, , P, 0.059, log 2, n, P1, , c, 0.0591, log 2 ,, n1, c1, , where c2 > c1 for spontaneous reaction, , 17. CASES OF ELECTROLYSIS, E ocell, , 2.303 RT, log K c, 2F, , 17.1 Electrolysis of molten sodium chloride, 2NaCl (l ) U 2Na+ (l ) + 2Cl– (l ), , E ocell, , 2.303 u 8.314 u 298, log K c, 2 u 96500, , 0.0591, log K c, 2, , o, In general, E cell, , or,, , 0.0591, log K c, n, , o, n E cell, log KC =, 0.0591, , 16. CONCENTRATION CELLS, If two electrodes of the same metal are dipped separately, into two solutions of the same electrolyte having different, , The reactions occurring at the two electrodes may be, shown as follows :, At cathode :, 2Na+ + 2e– o 2Na, , E0 = – 2.71 V, , At anode :, 2Cl– o Cl2 + 2e–, , E0 = – 1.36V, , Overall reaction :, 2Na+ (l ) + 2 Cl– (l ), or 2NaCl (l ), , 2Na (l ) + Cl2 (g), , 2Na (l ) + Cl2 (g), At cathode At anode

Page 5 :
ELECTROCHEMISTRY, , 17.2 Electrolysis of an aqueous solution of sodium chloride, Na+(aq) + Cl– (aq), , NaCl (aq), , These are used in small equipments like watches, hearing aids., , (almost completely ionized), , Anode : Zn – Hg Amalgam, , H2O (l ) U H+(aq) + OH–(aq), , Cathode : Paste of HgO and carbon, Electrolyte : Paste of KOH and ZnO, , (only slightly ionized), , Anode : Zn (Hg) + 2OH–, , At cathode :, E0 = – 2.71V, , 2Na+ + 2e–, , 2Na, , 2H2O + 2e–, , H2 + 2OH– E0 = – 0.83V, , Thus H2 gas is evolved at cathode value Na+ ions remain, in solution., At anode :, , 2Cl–, , ZnO (s) + H2O + 2e–, Hg (l) + 2OH–, , Cathode : HgO (s) + H2O + 2e–, , Overall Reaction : Zn (Hg) + HgO (s), , ZnO (s) + Hg (l), , The cell potential is approximately 1.35V and remains, constant during its life., 18.4 Secondary Batteries, , O2 + 4H+ + 4e– E0 = – 1.23V, , 2H2O, , 18.3 Mercury cells, , Cl2 + 2e–, , E0 = – 1.36V, , Thus, Cl2 gas is evolved at the anode by over voltage, concept while OH– ions remain in the solution., , 18. BATTERIES, , Secondary cells are those which can be recharged again, and again for multiple uses. e.g. lead storage battery and, Ni – Cd battery., 18.5 Lead Storage Battery, Anode : Lead (Pb), Cathode : Grid of lead packed with lead oxide (PbO2), , When Galvanic cells are connected in series to obtain a, higher voltage the arrangement is called Battery., 18.1 Primary Batteries, , Electrolyte : 38% solution of H2SO4, Discharging Reactions, , Primary cells are those which can be used so long the, active materials are present. Once they get consumed the, cell will stop functioning and cannot be re-used. Example, Dry Cell or Leclanche cell and Mercury cell., , Anode: Pb(s) + SO42–(aq), , Cathode: PbO2(s) + 4H+(aq) + SO42–(aq) + 2e–, PbSO4(s) + 2H2O(l), , 18.2 Dry cell, , Overall Reaction : Pb(s) + PbO2(s) + 2H2SO4(aq), , Anode : Zn container, Cathode : Carbon (graphite) rod surrounded by powdered, MnO2 and carbon., Electrolyte : NH4Cl and ZnCl2, Reaction :, Anode : Zn, , PbSO4(s) + 2e–, , Zn2+ + 2e–, , Cathode : MnO2 + NH 4 , e–, , 2PbSO4(s) + 2H2O(l), To recharge the cell, it is connected with a cell of higher, potential and this cell behaves as an electrolytic cell, and the reactions are reversed. Pb(s) and PbO 2(s) are, regenerated at the respective electrodes.These cells, deliver an almost consistent voltage., Recharging Reaction : 2PbSO4(s) + 2H2O(l), , PbO2(s) + 2H2SO4(aq), , MnO (OH) + NH3, , The standard potential of this cell is 1.5 V and it falls as, the cell gets discharged continuously and once used it, cannot be recharged., , Pb(s) +, , 19. FUEL CELLS, A fuel cell differs from an ordinary battery in the sense, that the reactants are not contained inside the cell but are

Page 6 :
ELECTROCHEMISTRY, externally supplied from an external reservoir. Fuel cell is, used in space vehicles and in this cell the two gases are, supplied from external storages. In this cell carbon rods, are used as electrodes with KOH as the electrolyte., 4OH– (aq), , Cathode : O2 (g) + 2H2O (l) + 4e–, Anode : 2H2 (g) + 4OH– (aq), , and iron is protected. This method of protecting one metal, by the other is also called Cathodic Protection., , 4H2O (l) + 4e–, , overall Reaction : 2H2(g) + O2 (g), , 2H2O (l), , 21. CONDUCTANCE (G), It is the reciprocal of resistance and may be defined as the, ease with which the electric current flows through a, conductor., 1, G, R, SI unit is Siemen (S)., 1 S = 1 ohm–1 (mho), , 22. CONDUCTIVITY (N, N), 20. CORROSION, It involves a redox reaction and formation of an, electrochemical cell on the surface of iron or any other metal., At one location oxidation of iron takes place (anode) and, at another location reduction of oxygen to form water takes, place (cathode). First Fe gets oxidised to Fe2+ and then in, the presence of oxygen it forms Fe3+ which then reacts, with water to form rust which is represented by Fe2O3.xH2O., Anode : 2Fe (s) o 2 Fe2+ + 4e– Eº = + 0.44 V, Cathode : O2 (g) + 4H + 4e o 2H2O (l) Eº = 1.23 V, +, , –, , It is the reciprocal of resistivity (U)., 1 1 A, A, Gu, N, u, U R A, A, Now if A = 1 cm and A = 1 cm2, then N = G.., Hence, conductivity of an electrolytic solution may be, defined as the conductance of a solution of 1 cm length, with area of cross-section equal to 1 cm2., , 23. FACTORS AFFECTING ELECTROLYTIC, CONDUCTANCE, , Overall R × N :, 2Fe (s) + O2 (q) + 4H+ o 2Fe2+ + + 2H2O Eºcell = 1.67 M, , 23.1 Electrolyte, An electrolyte is a substance that dissociates in solution to, produce ions and hence conducts electricity in dissolved, or molten state., Examples : HCl, NaOH, KCl (Strong electrolytes)., CH3–COOH, NH4OH (Weak electrolytes)., , Rusting of iron can be avoided by painting it or by coating, it with some other metals like Zinc. The latter process is, known as Galvanisation. As the tendency of Zn to get, oxidised is more than iron it gets oxidised in preference, , The conductance of electricity by ions present in the, solutions is called electrolytic or ionic conductance. The, following factors govern the flow of electricity through a, solution of electrolyte.

Page 7 :
ELECTROCHEMISTRY, , (i), , (ii), , (iii), , (iv), , Nature of electrolyte or interionic attractions : Lesser, the solute-solute interactions, greater will be the freedom, of movement of ions and higher will be the conductance., Solvation of Ions : Larger the magnitude of solute-solvent, interactions, greater is the extent of solvation and lower, will be the electrical conductance., The nature of solvent and its viscosity : Larger the solventsolvent interactions, larger will be viscosity and more will, be the resistance offered by the solvent to flow of ions, and hence lesser will be the electrical conductance., Temperature : As the temperature of electrolytic solution, rises solute-solute, solute-solvent and solvent-solvent, interactions decreases, this results in the increase of, electrolytic conductance., , 24. MEASUREMENT OF CONDUCTANCE, 1 A, u The value of Ncould be known,, R A, if we measure l, A and R. The value of the resistance of, the solution R between two parallel electrodes is, determined by using ‘Wheatstones’ bridge method, (Fig.), , As we know, N, , 25. MOLAR CONDUCTIVITY (/m), It may be defined as the conducting power of all the ions, produced by dissolving one mole of an electrolyte placed, between two large electrodes at one centimeter apart., Mathematically,, /m, , N u V, / m, , N u1000, C, , where, V is the volume of solution in cm3 containing 1, mole of electrolyte and C is the molar concentration., , Units :, , /m, , N u 1000, C, , S cm 1, mol cm 3, , = ohm–1 cm2 mol–1 or S cm2 mol–1, , 26. EQUIVALENT CONDUCTIVITY (/eq), It is conducting power of one equivalent of electrolyte, placed between two large electrodes at one centimeter apart., Mathematically :, / eq, , Nu v, , / eq, , N u1000, N, , Where, v is the volume of solution in cm3 containing, 1 equivalent of electrolyte and N is normality., Units :, / eq, , N u1000, N, , S cm1, equivalent cm 3, , It consists of two fixed resistance R3 and R4, a variable, resistance R1 and the conductivity cell having the unknown, resistance R2. The bridge is balanced when no current, passes through the detector. Under these conditions,, R1, R2, , R3, R4, , or, , R2, , R 1R 4, R3, , Ohm1 cm 2 equivalent 1, S cm 2 equivalent 1, or, , 27. VARIATION OF CONDUCTIVITY AND MOLAR, CONDUCTIVITY WITH DILUTION, Conductivity decreases with decrease in concentration,, this is because the number of ions per unit volume that, carry the current in the solution decreases on dilution., Molar conductivity / m, , N u V increases with decrease, , in concentration. This is because the total volume V of, solution containing one mole of electrolyte also increases.

Page 8 :
ELECTROCHEMISTRY, It has been found that the decrease in Non dilution of a, solution is more than compensated by increases in its, volume., Graphic representation of the variation of / m vs c, , Here, O o and Oo are the limiting molar conductivities of, cations and anions respectively., , 30. APPLICATIONS OF KOHLRAUSCH’S LAW, 30.1 (i) Calculation of molar conductivities of weak, electrolyte at infinite dilution, For example, molar conductivity of acetic acid at infinite, dilution can be obtained from the knowledge of molar, conductivities at infinite dilution of strong electrolyte like, HCl, CH3COONa and NaCl as illustrated below., , o, ªOo,  OoNa º  ¬ª OHo   O Cl ¼º  ¬ªOoNa  OCl,  º, ¼, ¬ CH3  COO, ¼, , o, i.e. / m CH3  COOH, , 28. LIMITING MOLAR CONDUCTIVITY (/m), The value of molar conductivity when the concentration, approaches zero is known as limiting molar conductivity or, molar conductivity at infinite dilution. It is possible to, o, determine the molar conductivity at infinite dilution / m in, case of strong electrolyte by extrapolation of curve of, / m vs c. On contrary, the value of molar conductivity of, weak electrolyte at infinite dilution cannot be determined, by extapolation of the curve as the curve becomes almost, parallel to y-axis when concentration approaches to zero., The mathematical relationship between / m and / om for, strong electrolyte was developed by Debye, Huckel and, Onsagar. In simplified form the equation can be given as, , where /, , 30.2 (ii) Determination of Degree of Dissociation, of Weak Electrolytes, , f, m, , is the molar conductivity at infinite dilution, , and b is a constant which depends on the nature of the, solvent and temperature., , 29. KOHLRAUSCH’S LAW, It states that the limiting molar conductivity of an electrolyte, can be represented as the sum of the individual contributions, of the anion and cation of the electrolyte. In general, if an, electrolyte on dissociation gives v+ cations and v– anions, then its limiting molar conductivity is given by, / fm, , v O o  v  Oo, , / cm, / mo, , Degree of dissociation D, , 30.3 (iii) Determination of Dissociation Constant, (K) of Weak Electrolytes:, , also, , K, , cD 2, 1 D, , D, , / cm, / fm, , / fm  b c1/ 2, , /m, , / mo CH3  COONa  / om HCl  / om NaCl, , ?, , K, , c / cm / / fm, , 2, , 1  / cm / / fm, , C / cm, , 2, , / fm / fm  / cm, , 31. USE OF 'G IN RELATING EMF VALUES OF, HALF CELL REACTIONS, When we have two half cell reactions such that on adding, them we obtain another half cell reaction then their emfs, cannot be added directly. But in any case thermodynamic, functions like 'G can be added and emf values can be related, through them. Consider the following three half cell reactions:, Fe2+ + 2e– o Fe, , E1

Page 9 :
ELECTROCHEMISTRY, Fe3+ + 3e– o Fe, , E2, , Fe3+ + e– o Fe2+ E3, We can easily observe that the third reaction can be, obtained by subtracting the first reaction from the second., But the same relation does not apply on the emf values., That is, E3 z E2 – E1. But the 'G values can be related, according to the reactions. That is,, , 5., , D, , / cm, / fm, , D = Degree of dissociation, , where,, , / cm = Molar conductivity at a given, concentration, 6., , For a weak binary electrolyte AB, , 'G3 = 'G2 – 'G1, K, , – n3FE3 = – n2FE2 + n1FE1, – E3 = – 3E2 + 2E1, , c / cm, , cD 2, 1 D, , 2, , / fm / fm  / cm, , where, K = Dissociation constant, , ŸE3 = 3E2 – 2E1, , Eocell, , E ocathode  E oanode, = Eo Right + Eo left, , NOTE, , 7., , Nernst equation for a general electrochemical reaction, , , We should always remember that emf values are additive, only when two half cell reactions are added to give a, complete balanced cell reaction. In any other case we, will be using 'G values to obtain relations between emf, values., , ne, aA + bB , o cC + dD, , E cell, , E cell, , 32. FORMULAE, 1., , R, , §A·, U ¨ ¸ Uu Cell constant, ©A¹, , where,, , E cell, , 8., , U= Resistivity, 2., , N, , 1, u cell constant, R, , 3., , /m, , log Kc =, , 9., , f, m, , where, / = Molar conductivity at infinite dilution x and y, are the number of cations and anions produced by one, formula unit of the electrolyte on complete dissociation., , A B, 0.059, , log, c, d, n, C D, , c, , E, , D, , a, , B, , d, , b, , b, , at 298 K, , n, E ocell, 0.0591, ,  nFE ocell (Creterion of spontaneity), , 'r G o, , 2.303RT log K c, , where, 'rGo = Standard Gibbs energy of the reaction., 10., , Q=I×t, where, , Q = Quantity of charge in coulombs, I = Current in amperes, t = Time in seconds, , M = Molarity of the solution., / mf (Ax By) = x / fm (Ay+) + y / fm (Bx–), , o, cell, , b, , 'r G o, , where, / m = Molar conductivity, , 4., , C, 2.303RT, log, , nF, A, , B, , where, Kc = Equilibrium constant., , where, N = Conductivity or specific conductance, N u 1000, M, , E, , o, cell, , a, , D, , d, , C, RT, , In, nF, A, , a, , R = Resistance, A = Area of cross-section of the electrodes., , E, , c, , o, cell, , 11., , m=Z×I×t, where, , m = mass of the substance liberated at the, electrodes, Z = Electrochemical equivalent., , where E = Equivalent weight = E/96500