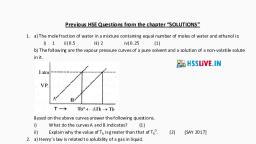
Page 1 :
Unit -2, THEORY OF DILUTE SOLUTIONS, 1) What
is
solution?
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, , [1]
, ,
, ,
, ,
, ,
, , [1]
, , A:
It
is
a
homogenous
mixture
of
two
or
more
compounds.
, 2) What
is
dilute
solution?
, ,
, ,
, ,
, ,
, , A:
It
is
a
solution
in
which
solute
concentration
is
very
less.
, 3) Give
an
example
for
solid-‐solid
solution
,
,
,
,
,
, [1]
, A:
Copper
dissolved
in
gold.
, 4) Give
an
example
for
gas-‐gas
solution
,
,
,
,
,
,
, [1]
, A:
Mixture
of
oxygen
and
nitrogen
gases.
, 5) Give
an
example
for
gas-‐solid
solution
,
,
,
,
,
,
, [1]
, A:
Solution
of
hydrogen
in
palladium.
, 6) Give
an
example
for
liquid-‐solid
solution
,
,
,
,
,
, [1]
, A:
Amalgam
of
mercury
with
sodium.
, 7) Give
an
example
for
liquid-‐liquid
solution
,
,
,
,
,
, [1]
, A:
Ethanol
dissolved
in
water.
, 8) Give
an
example
for
solid-‐gas
solution
,
,
,
,
,
,
, [1]
, A:
Camphor
in
nitrogen
gas.
, 9) Define
mole
fraction
and
give
the
equation
to
calculate
it.
,
,
,
, [2]
, A:Mole
fraction
is
the
ratio
of
number
of
moles
of
one
component
to
the
total
number
of
moles
, of
all
the
components
in
the
solution.
, , XA =, , XB =, , n, , A
, n + nB, A, nB, n + nB, A, ,
, , 10)Define
molarity
and
give
the
equation
to
calculate
it.
,
,
,
,
, A:
Number
of
moles
of
the
solute
present
per
liter
solution
is
known
as
molarity.
, n,
, M= B, V,
, , [2]
, , 11)Define
molality
and
give
the
equation
to
calculate
it.
,
,
,
, A:
Number
of
moles
of
the
solute
present
perkgsolvent
is
known
as
molality.
, n, M= B, WA, , [2]
Page 2 :
12)Define
the
term
solubility
of
a
substance.
,
,
,
,
,
, [1]
, A:
Solubility
of
a
substance
is
its
maximum
amount
that
can
be
dissolved
in
a
specified
, amount
of
solvent
at
a
specified
temperature
, 13)State
Henry’s
law.
,
,
,
,
,
,
,
,
,
, [2]
, A:
Henry’s
Law:
At
constant
temperature
solubility
of
a
gas
in
a
liquid
is
directly
proportional
, to
the
partial
pressure
of
gas
present
above
the
solution.
, OR
,
, At
constant
temperature
the
partial
pressure
of
the
gas
in
vapor
phase
(p)
is
proportional
, to
the
mole
fraction
of
the
gas
(x)
in
the
solution.
, , Mathematically p ∝ x ;, , p = KH x., , Where KH is Henry’s law constant. KH depends on the nature of the gas., ,
,
,
,
,
,
,
, , Partial
pressure
of
a
gas
, ,
, 14)Write
the
plot
which
shows
relation
between
partial
pressure
of
a
gas
v/s
its
mole
, fraction.
,
,
,
,
,
,
,
,
,
,
, [2]
, A:
, , Mole
fraction.
, 15)Mention
the
factors
affecting
solubility
of
a
gas
in
liquid.
,
,
,
, [2]
, A:
1.
Temperature
2.
Pressure
, 16)Explain
how
temperatures
effect
the
solubility
of
a
gas
in
liquid.
,
,
, [2]
, A:
Solubility
of
gases
in
liquid
decreases
with
rise
in
temperature.
According
to
Le
Chatelier’s
, Principle,as
dissolution
is
an
exothermic
process,
the
solubility
should
decrease
with
increase
, of
temperature.
, 17)Explain
how
pressure
effects
the
solubility
of
a
gas
in
liquid.
,
,
, [1]
, A:
The
solubility
of
gases
increases
with
increases
of
pressure.
, 18)Mention
the
applications
of
Henry’s
law.
,
,
,
,
,
, [3]
, A:
(a)
To
increase
the
solubility
of
CO2
insoft
drink
and
soda
water,
the
bottle
is
sealed
under
, high
pressure.
Page 3 :
(b)
To
avoid
bends,
as
well,
the
toxic
effects
of
high
concentration
of
nitrogen
in
the
blood,
the
, tanks
used
by
scuba
divers
are
filled
with
air
dilute
with
helium.
, (c)
At
high
altitudes
the
partial
pressure
of
oxygen
is
less
than
that
at
the
ground
level.
This
, leads
to
low
concentrations
of
oxygen
in
the
blood
and
tissues
of
people
living
at
high
, altitudes
or
climbers.
,
, 19)State
Raoult’slaw
of
liquid-‐liquid
dilute
solutions.
,
,
,
,
, [2]
, A:
The
partial
vapour
pressure
of
each
component
of
the
solution
is
directly
proportional
to
, its
mole
fraction
present
in
solution.
, Thus,
for
component
1
, P1
⍺
x1
, And
, p1
=
p10x1
, 20)What
are
ideal
solutions?
,
,
,
,
,
,
,
,
, [1]
, A:
The
solution
which
obey
Raoul’s
law
over
the
entire
range
of
concentration
are
known
as
, ideal
solution
, 21)Mention
the
characters
of
ideal
solutions.
,
,
,
,
,
, [3]
, A:
, Ideal
,
, I.
It
obeys
Raoults
law
is
obeyed
at
all
temperature
,
, and
concentration
,
, P
=
PA
+
PB
,
, II. ∆
V
mix
=
O
i.e.,
there
is
no
change
in
volume
on
,
, mixing
,
, III. ∆Hmix
=
O
i.e.,
there
is
no
enthalpy
change
when
,
, ideal
solution
formed
,
, IV. It
doesn’t
form
azeotropic
mixture
,
, V. Force
of
attraction
between
A―A,
B―B is similar,
, as A―B
,
,
,
, 22)What
are
non-‐ideal
solutions?
,
,
,
,
,
,
,
, [1]
, A:
When
a
solution
does
not
obey
Raoult’s
law
over
the
entire
range
of
concentration,
then
it
, is
called
non-‐ideal
solution.
, 23)Mention
the
types
of
non-‐ideal
solutions.
,
,
,
,
,
, [1]
, A:
There
are
two
types
, (a)
Non-‐ideal
solution
with
positive
deviation
from
Raoult’s
law
, (b)
Non-‐ideal
solution
with
negative
deviation
from
Raoult’s
law
,
, 24)Give
an
example
for
non-‐ideal
solution
with
positive
deviation
from
Raoult’s
law.
[1]
, A:
Mixtures
of
ethanol
and
acetone
Page 4 :
25)Give
an
example
for
non-‐ideal
solution
with
negative
deviation
from
Raoult’s
law.
[1]
,
, A:
An
example
of
this
type
is
a
mixture
of
phenol
and
aniline.
,
, 26)What
are
azeotropes?
Give
example.
,
,
,
,
,
,
, [2]
, A:
Azeotropes
are
binary
mixtures
having
the
same
composition
in
liquid
and
vapour
phase
, and
boil
at
a
constant
temperature.
, For
example:
ethanol-‐water
mixture
,
, 27)State
Raoult’s
law
of
relative
lowering
of
vapour
pressure.
,
,
,
, [1]
, A:
Relative
lowering
of
vapour
pressure
is
equal
to
the
mole
fraction
of
the
solute.
,
, 28)Define
colligative
property.
,
,
,
,
,
,
,
, [1]
, A:
The
properties
depend
on
the
number
of
solute
particles
irrespective
of
their
nature
, relative
to
the
total
number
of
particles
present
in
the
solution.
Such
properties
are
called
, colligative
properties
,
, 29)Mention
four
colligative
properties
of
dilute
solutions.
,
,
,
, [2]
, A:
Relative
lowering
of
vapour
pressure
, I., II., III., , Elevation
in
Boiling
point
, Depression
in
Freezing
point
, Osmotic
pressure
, , 30)Define
the
term
relative
lowering
of
vapour
pressure.
,
,
,
, [2]
, A:
It
is
the
ratio
of
lowering
of
vapour
pressure
to
the
vapour
pressure
of
the
pure
solvent
, , Po − P, = Relative lowering of V.P
, Po, 31)What
is
elevation
in
boiling
point?
,
,
,
,
,
,
, A:
Elevation
in
boiling
point
is
the
difference
between
the
boiling
point
of
the
solution
, , [1]
, , containing
non-‐volatile
solute
and
the
boiling
point
of
the
pure
solvent
, ∆Tb
=
T
–
To
, 32)Give
the
relation
between
elevation
in
boiling
point
and
molecular
mass
of
solute.
[2]
, A:
, , ΔTb = Kb, , w 2 × 1000,
, w1 × M 2, , Where w2 is mass of solute, w1 is the mass of the solvent; M2 is molar mass of the solute
Page 5 :
33)Give
the
S.I.unit
of
ebullioscopic
constant
or
boiling
point
elevation
constant
or
molal
, elevation
constant.
,
,
,
,
,
,
,
,
,
, [1]
, A:
The
unit
of
Kb
is
K
kg
mol-‐1
,
, 34)What
is
depression
infreezing
point?
,
,
,
,
,
,
, [1]
,
, A:
It
is
the
decrease
in
the
freezing
point
of
solution
when
non-‐volatile
solute
is
added
into
, solvent.
, 35)Give
the
relation
between
depression
infreezing
point
and
molecular
mass
of
solute.[2]
, A:
, , w2, M2, ΔTf = Kf, w1, 1000, , ∴ M2 =, , K f × 1000 × w 2, where M2 is molar mass of the solute., ΔTf × w1, , Note: Values of Kf and Kb of the solvent depends on their molecular mass and ΔHfusion and ΔHvap, of the solvent respectively.,
, 36)Give
the
S.I.unit
of
cryoscopic
constant.
,
,
,
,
,
, A:
The
unit
of
Kf
is
K
kg
mol-‐1
,
, 37)Draw
the
plot
showing
elevation
in
boiling
point
in
a
solution.
, A:
,
, ,
,
,
, ,
, ,
,
, , Vapour
pressure
, ,
, ,
, ,
, ,
, ,
, ,
, , Solvent
,
, , ―∆Tb
―
, Tb0
, , Temperature/K
,
,
,
, , Solution
, , Tb
, ,
, ,
, , [1]
, ,
, ,
, , [2]
Page 6 :
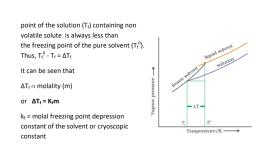
38)Draw
the
plot
showing
depression
in
freezing
point
in
a
solution.
, ,
, ,
, , [2]
, ,
, Vapour
pressure
, ,
,
,
,
,
, ,
, ,
, ,
,
, , Frozen
solvent
, ,
, Liquid
solvent
, , ―∆Tf―
, Tf
, ,
, , Solution
, , Tfo
, , Temperature/K
, , 39)Define
osmosis.
,
,
,
,
,
,
,
,
,
, A:
The
process
of
movement
of
solvent
particles
from
lower
concentration
to
higher
, , [1]
, , concentration
through
semi-‐permeable
membrane
to
attain
equilibrium
is
called
osmosis.
,
,
,
,
,
,
, 40)What
is
osmotic
pressure
and
give
its
relation
with
concentration
of
solution.
, [2]
, A:
The
amount
of
external
pressure
required
to
stop
the
osmosis.
, =
CRT
, Where:
=
osmotic
pressure,
R
=
gas
constant,
T
=
temperature,
C
=
concentration
of
solution.
,
, 41)
What
are
isotonic
solutions?
,
,
,
,
,
,
,
, [1]
, A:
Two
different
solutions
having
sameosmotic
pressure
are
called
isotonic
solutions
, 42)What
are
hypertonic
solutions?
,
,
,
, A:
The
solution
having
more
osmotic
pressure
than
other
, ,
, ,
, ,
, ,
, , [1]
, , 43)What
are
hypotonic
solutions?
,
,
,
, A:
The
solution
having
less
osmotic
pressure
than
other
, ,
, ,
, ,
, ,
, , [1]
Page 7 :
44)Explain
the
application
of
reverse
osmosis
in
desalination
of
water.
,
, [2]
, A:
When
pressure
more
than
osmotic
pressure
is
applied,
pure
water
is
squeezed
out
of
the
, sea
water
through
the
membrane.
A
variety
of
polymer
membranes
are
available
for
this
, purpose.
, The
pressure
required
for
the
reverse
osmosis
is
quite
high.
A
workable
porous
membrane
is
, a
film
of
cellulose
acetate
placed
over
a
suitable
support.
Cellulose
acetate
is
permeable
to
, water
but
impermeable
to
impurities
and
ions
present
in
sea
water.
, 45)What
is
reverse
osmosis?
,
,
,
,
,
,
,
,
, [1]
, A:
Movement
of
solvent
particles
from
higher
, concentration
to
lower
concentration
through
a
semi
, permeable
membrane,
when
pressure
is
applied
, greater
than
osmotic
pressure
,
,
,
, 46)What
is
abnormal
molar
mass?
,
,
,
,
,
,
,
, [1]
, A:
A
molar
mass
that
is
either
lower
or
higher
than
the
expected
or
normal
value
is
called
as
, abnormal
molar
mass.
, 47)
Define
Vant
hoff
factor
, , Van’t Hoff factor ‘i’ to account for the extent of association or dissociation of a solute in a solvent, is, i=, , Normal molar mass, Abnormal molar mass, , or, i=, , observed colligative property, calculated colligative property, , or, i=, , total number of moles of particles after association or dissociation, Number of moles of particles before association or dissociation, , 48)What
is
the
value
of
i
for
NaCl.
, A:
2
,
, 49)What
is
the
value
of
i
for
K2SO4.
, A:
3
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, , [1]
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, , [1]
Page 8 :
50)What
is
the
value
of
i
for
sugar.
,
,
,
,
,
,
,
, A:
1
, 51)What
is
the
value
of
i
for
glucose.
,
,
,
,
,
,
,
, A:
1
, 52)On
what
factor
the
colligative
property
depends
on.
,
,
,
,
, A:
It
depends
on
number
of
moles
of
solute
particles
but
not
on
the
nature
of
the
solute.
, 53)Write
the
mathematical
equation
of
Raoults
law
in
case
of
non-‐volatile
solute.
, , [1]
, [1]
, [1]
, [1]
, , A:
If
one
of
the
components
(solute)
is
non-‐volatile
then
the
equation
of
Raoults
law
is.
, PB=
O
, P
=
PA
+
PB
, P
=
PA
+
O
, P
=
PA
O, P
=
PA .
XA
,
, 54)Write
the
differentiate
between
non-‐ideal
solutions
with
positive
deviation
and
, negative
deviation
from
Raoult’s
law
,
,
,
,
,
,
,
,
,
,
,
,
,
, , Positive
deviation
,
, (a)In
this
solution
solvent
–
, solute
interaction
is
weaker
, than
solvent
–
solvent,
, solute-‐solute
interactions
, (b)
P
>
PA
+
PB
, (c)
∆
V
>
O
, (d)
∆H
=
positive
, (e)
It
forms
azeotrope
with
, minimum
boiling
point
, ,
, 55)Define
lowering
of
vapour
pressure?
, , Negative
deviation
,
, (a)
In
this
solution
solvent
, –
solute
interaction
is
, stronger
than
solvent
–
, solvent,
solute-‐solute
, interactions
, (b)
P
<
PA
+
PB
, (c)
∆
V
<
O
, (d)
∆H
=
negative
, (e)It
forms
azeotrope
with
, maximum
boiling
point
,
,
,
,
,
, ,
, ,
, , [2]
, , [1]
, , A:
It
is
defined
as
the
difference
between
the
vapor
pressure
of
the
solvent
in
pure
state
and
the
, vapour
pressure
of
the
solution
, ∆P
=
Po
–
P
, 56)State
Roult’s
law
of
relative
lowering
of
vapour
pressure
, ,
, ,
, ,
, , [1]
, , A:
It
states
that
the
relative
lowering
of
vapour
pressure
is
equal
to
the
mole
fraction
of
the
, solute
Page 9 :
57)Why
sea
water
freezes
below
00C?
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, , [1]
, ,
, A:
Sea
water
freezes
below
00C
due
to
the
presence
of
the
non-‐volatile
solute
dissolved
in
the
, water.
,
, 58)Derive
the
equation
to
calculate
molecular
mass
of
unknown
solute
using
Raoult’s
law
, of
relative
lowering
of
V.P
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, , [3]
, , A:
According
to
Raoult’s
law
relative
lowering
of
vapour
pressure
is
equal
to
the
mole
fraction
, of
the
solute.
, , Po − P, = X B
, Po, nB, Po − P,
, =, n + nB, Po, A, nB<<<nA
for
dilute
solution
, So
we
can
neglect
nB
in
denominator
, , Po − P n B,
, =, n, Po, A, WB, o, P − P MB,
, =, WA, Po, MA, , Po − P WB MA,
, =, W MB, Po, A, WB .M A ⎛ Po ⎞, MB =, ⎜, ⎟
, WA ⎝ Po − P ⎠
Page 10 :
Numerical
problems
, 1. A
solution
containing
2.56
g
sulphur
in
100
g
CS2
gave
a
freezing
point
lowering
of
0.383
K.
, Calculate
the
molar
mass
of
sulphur
molecules.
Given
Kf
of
CS2
=
3.83
K
kg
mol 1.
, Ans.
ΔTf
=
0.383
K,
Kf
=
3.83
K
kg
mol 1
, −, , −, , ΔTf
=
Kf
×
m
, , W2, M, ;
ΔTf
=
Kf
×
2
, W1, 1000, , M2
(molar
mass
of
sulphur
molecules)
=
, , 2.56 ×1000 × 3.83,
=
256
g
mol 1
, 100 × 0.383, −, , 2. 100
g
of
water
has
3g
of
urea
dissolved
in
it.
Calculate
the
freezing
point
of
the
solution.
Kf
for
, water
=
1.86
K
kg
mol 1,
molar
mass
of
urea
=
60
g
mol 1,
freezing
point
of
water
=
273.15
K
, (0°C)
, −, , −, , Ans.
ΔTf
=
Kf
×
m
, , W2, M, ;
ΔTf
=
1.86
×
2
, W1, 1000, ,
, ,
, , ΔTf
=
Tf0 − Tf
, ,
, , ΔTf
=
1.86
×, , ∴
Tf
=
273.15
−
0.93
=
272.22
, , 3 × 1000,
=
0.93
, 60 × 100, , or
, , −0.93°C
, , 3. Human
blood
has
osmotic
pressure
of
7.2
atm
at
body
temperature
of
37°C.
Calculate
the
, molar
concentration
of
solute
particles
in
blood.
Given
R
=
0.0821
L
atm
K 1.
, −, , Ans.
π
=
CRT
, , ;
, , C
=
, , π,
, RT, , C
(molar
concentration)
=
, ,
, , T
=
273
+
37
=
310
K
, , 7.2,
=
0.2828
M
, 0.0821× 310, , 4. Vapour
pressure
of
benzene
is
200
mm
of
Hg.
2g
of
a
non-‐volatile
solute
in
78
g
benzene
has
, vapour
pressure
of
195
mm
of
Hg.
Calculate
the
molar
mass
of
the
solute.
Molar
mass
of
, benzene
=
78
g
mol 1.
, −, , Ans.
, ,
, , P° − P n 2, =
;
, P°, n1, , W2, P° − P M 2,
, =, W1, P°, M1, , Molar
mass
of
solute
(M2)
=
, , 2, M, 200 − 195,
=
2 ;
, 78, 200, 78, , 200 × 2,
=
80
g
mol 1
, 5, −
Page 11 :
5. 500
g
of
water
containing
27
g
of
a
non-‐volatile
solute
will
boil
at
100.156°C.
Calculate
the
, molar
mass
of
the
solute.
Given
boiling
point
of
water
=
100°C,
Kb
=
0.52
K
kg
mol 1.
, −, , W2, M, Ans.
ΔTb
=
Kb
×
m
;
ΔTb
=
Kb
×
2
, W1, 1000, ,
, , Molar
mass
of
solute
(M2)
=
,
,
, , 0.52 × 27 ×1000,
=
180
g
mol 1.
, 500 × 0.156, −