Page 2 :
SK, , Mixtures:- A combination of two or more elements or, compouds in any proportion is called mixture, MIXTURE, , Homogenous Mixture, The composition is same, throughout the sample, , Heterogenous Mixture, The composition is not same, throughout the sample, , Example, , Example, , Sugar in water, Seawater, Air, , Oil in water, Sand and water
Page 3 :
SK, , Solutions, Solvent, , Solute, The component, other than, solvent, , the component, which is, present in, largest quantity, , 3
Page 4 :
SK, , Some Definitions, A, solution, is, a, homogeneous mixture of 2, or more substances called, components., A solution containing two, component is called binary, solution., In solution ,the component, which is present in the largest, quantity is called solvent., The components other than, solvent are called solutes, 4
Page 5 :
SK, , Depending, upon the, nature of, solute and, solvent, SOLUTE-, , lesser, amount, SOLVENT, , –, , largest, quantity, Solute +, Solvent =, Solution, , Solute, , Solvent, , Example, , Gas, , Gas, , Mixture of gases, Air, , Liquid, , Gas, , Water vapour in air,Mist, , Solid, , Gas, , Vapours of iodine in, air,Camphor in N2, , Gas, , Liquid, , CO2 dissolved in, water(aerated soft drink), , Liquid, , Liquid, , Mixture of miscible liquids, (alcohol in water), , Solid, , Liquid, , Salt in water,Sugar in water, , Gas, , Solid, , Solution of H2 in, Pd(occlusion), , Liquid, , Solid, , Hg in Zn,Hg in Au, , Solid, , Solid, , Homogenous mixture of, two or more metals (alloys), ,Cu in Au ,Zn in Cu (Brass)
Page 6 :
SK, , Expressing Concentration, Mass percentage, Volume percentage, Mass by volume percentage, Parts per million, Mole Fraction (χ), Molarity (M), Molality (m), Normality(N), 6
Page 7 :
SK, , Mass percentage, Mass percentage (w/w): The mass percentage of a, component in a solution is the mass of the component per, 100gm of the solution, , Mass % of a component, = Mass of the component in the solution ×100, Total mass of the solution, If WB is the mass of the solute and WA is the mass of the, solvent, Mass % of A =, WA, x100, WA+ W, Mass % of B =, , WB, , B, , x 100, , WA+W B
Page 8 :
SK, , Volume percentage, The volume percentage of a component in, a solution is defined as the volume of the, component per 100 parts by volume of the, solution:, Volume % of a component =, Volume of the component ×100, Total volume of solution
Page 9 :
SK, , Mass by volume percentage, It is the mass of the solute, dissolved in 100 ml of the solution, Mass/volume percentage=, Mass of the component in solution X100, Total volume of the solution
Page 10 :
SK, , Parts per million(PPM), When a solute is present in minute, , amount ,the concentration is expressed, in parts per million (ppm)., It is defined as the mass of the solute, , present per million parts by mass of, the solution., PPM= Mass of the component ×106, Total mass of the solution
Page 12 :
SK, , Molarity(M), It is number of moles of solute dissolved per, litre of the solution.It is represented by ‘M’, Morarity = Number of moles of solute, Volume of the solution in litre, Or Molarity = Number of moles of solute x1000, Volume of solution in mL, Unit mol/L or molL-1, or M, , Note:-, , or Molarity=Wx1000, M x V(mL), , The molarity of a solution changes with temperature, due to change in volume of the solution
Page 13 :
SK, , Molality, , It is the number of solute dissolved, per kg(1000gm) of solvent, Molality = Number of moles of solute, Weight of solvent in kg, Molality=Number of moles of solutex1000, Weight of solvent in gm, Or Molality=W1x1000 W2-weight of solvent, M1x W2, , Note:-, , Unit mol/Kg or molkg-1, or m, , Molality of solution does not change with, temperature .This is because mass of the solvent does not, change with change in temperature.Therefore molality is, considered better for expressing the concentration of, solution.
Page 14 :
SK, , Normality(N), Equivalent mass of acid = Molecular mass, Basicity, Basicity is the number of H+ ions given to the solution, , Equivalent mass of base = Molecular mass, Acidity, Acidity is the number of OH- given to solution, Normality is defined as the number of gram equivalent of, solute dissolved per litre of the solution .It is denoted by ‘N’, Normality(N) = Number of gram equivalent of solute, Volume of solution in litre, Or Normality= Mass of solute x 1000, , Eq. mass of solute x Volume of solution in ml, , or Normality = Wx1000, E x V (mL)
Page 19 :
Solubility of solid in Liquids, , The maximum amount of solute dissolved in, a given amount of solvent to form a saturated, solution at a particular temperature is called, solubility, , The solubility of a solid in liquids depends upon, 1.Effect of temperature :- In a saturated solution there, is an equillibrium .Therefore according to Le-chatlier, principle,if the dissolution process is endothermic,the, solubility increases with increase in temperature.If the, dissolution process is endothermic ,the solubility, decreases with rise in temperature., 2.Effect of pressure:-Pressure has no significant, effect on solubility of solids in liquids.This is because, solids & liquids are nearly incompressible and remain, unaffected by change in pressure
Page 20 :
Solubility of Gases in Liquids, The solubility of a gas in a liquid depends upon the, following factors., (i)Nature of the gas (ii) Temperature (iii) Pressure, (i) Nature of the Gas :- Generally easily liquifiable, gases are more soluble.Thus gases like CO2,HCl,NH3, etc are more soluble in water than gases like H2,O2 etc., (ii) Temperature:- With increase in temperature the, solubility of gases generally decreases., Due to this factor aquatic species are more, comfortable in cold water than warm water, (iii) Pressure:- The effect of pressure on the solubility, of gas is given by Henry’s law., It states that the solubility of gas in a liquid is directly, proportional to the pressure of the gas., 20
Page 21 :
Most commonly used form of Henry’s law states that the, molefraction of the gas in a solution (XB) is proportional, to the partial pressure of the gas in vapour phase, Partial pressure of the gas = KH .molefraction of the gas or, P = KH . X B, Where ‘ K H ‘ is Henry’s law constant, , Higher the value of KH at a given, pressure, lower is the solubility, of gas in liquid., molefraction of solute, , The value of KH increases with increase of temperature, , 21
Page 22 :
Applications of Henry’s Law, * To, , increase the solubility of CO2 in soft, drinks and sodawater,the bottle is sealed, at higher pressure, *A medical condition known as Anoxia, in people living at high altitudes or, climbers, A condition known as Bends, (Decompression sickness) in, Scuba divers, *, , o, 22
Page 23 :
Vapour pressure of a liquid, The pressure exerted by the vapour above the liquid, surface which is in equilibrium with the liquid at a given, temperature.The vapour pressure of a liquid depends on, two factors., (i)Nature of the liquid:- Each liquid has a characteristic, vapour pressure.It depends upon the magnitude of intermolecular, forces.Weaker the intermolecular forces,greater is the vapour pressure., , (ii)Temperature:- The vapour pressure of a liquid increases with, increasein temperature.At higher temperature,molecules will have, larger kinetic energy,therefore larger number of molecules will, escape into vapour state., When a small amount of a non volatile solute is added to solvent,the, vapour pressure of the solution is, found to be less than that of pure, solvent
Page 24 :
Raoult’s law for binary solution of volatile liquid, When two volatile liquids of A and B are mixed to form a, solution,the vapour phase consists of vapours of each, components.The partial pressure of each component, depends on molefraction of the corresponding component., , If PA and PB are the partial vapour pressure of the liquids A, and B in a solution and A and B are the molefraction.
Page 25 :
PA α A or PA = P°A.B PB α B or PB = P°B.B, Where P°A and P°B are the vapour pressure of pure, componets A and B respectively, , Raoult’s, , law, , states, , that, , at, , a, , given, , temperature ,for a solution of volatile liquids, the, partial vapour pressure of each component is, directly proportional to its molefraction, , 25
Page 28 :
Ideal Solutions, The solutions which obey Raoult’s law over the, entire range of concentration are known as, ideal solutions., The ideal solutions should have the following, characteristics, (i)It should obey Raoult’s law ie, PA = P0A .XA and, PB= P0B.XB, (ii)Heat change on mixing is zero ( ΔHmix = 0 ), since, there is no change in magnitude of the attractive forces in two, components the heat change on mixing is zero, , (iii)Volume change on mixing is zero ΔVmix = 0, In ideal solution ,the volume of the solution is, the sum of the volumes of components before, mixing., (iv)Substances forming an ideal solution have, similar structure
Page 30 :
Non-ideal solutions, The solution which do not obey Raoult’s law are called non-ideal, solutions.In non-ideal solutions,there is a change in volume and, heat when the two components are mixed., (i) PA # P0A .XA and PB# P0B.XB, (ii) Δ Hmixing # 0, (iii) ΔVmixing # 0, , The non-ideal solutions are further classified into two types, (i)Solution showing ‘+’deviation, (ii)Solution showing – ve deviation
Page 31 :
(i)Solution showing ‘+’deviation, Consider a binary solution of two components A and B.If the, A-B interaction are weaker than A-A and B-B interactions,the escaping, tendency of A and B molecules from the solutions becomes more.As a, result the partial vapour pressure of each component is higher than, that expected from Raoult’s law.Therefore the total vapour pressure of, the solution is greater than the vapour pressure as expected according, to Raoult’s law., PA > P0A .XA and PB > P0B.XB, >, The total vapour, pressure of the solution Ps > PA+ PB, Here Δ Hmixing= + ve , ΔVmixing = + ve, Eg:(i) Ethyl alcohol & cyclohexane (ii) Acetone & Benzene, (iii) Acetone & Cabondisulphide(iv)Ethyl alcohol & water, (v) Acetone & Ethyl alcohol, 31
Page 33 :
Azeotrope (constant boiling mixtures), The solution which boils at constant temperature and distilled over, completely at that temperature without any change in composition, are called azeotropes.These are of two types, (i)Minimum boiling azeotropes :- The solution which show positive, deviations from Raoult’s law are called minimum boiling, azeotropes,because they have a composition having minimum, boiling point.They have boiling points lower than either of the, components, Eg :- H2O (4.4%) & C2H5OH (95.6%), Boiling point of azeotrope is 78.10C, B.P 1000C, 78.60C, (ii)Maximum boiling azeotrope :- The solution which show, negative deviations from Raoult’s law are called maximum boiling, azeotropes,because they have a composition having maximum, boiling point.They have boiling points higher than either of the, Components, ., Eg (i) H2O (80%) & HCl (20%), Boiling point of azeotrope is 108.60C, B.P 1000C, 20.20C
Page 34 :
COLLIGATIVE PROPERTIES (Democratic properties), The properties of a solution which depends only on the number of, moles of solute particles but not the nature of the solute are called, colligative properties., The four important colligative properties are, (i)Relative lowering of vapour pressure (ii) Elevation of boiling point, (iii) Depression of freezing point, (iv) Osmotic pressure, (i)Relative lowering of vapour pressure, The presence of a nonvolatile solute means, that fewer solvent, particles are at the, solution’s surface, so, less solvent evaporates., 34
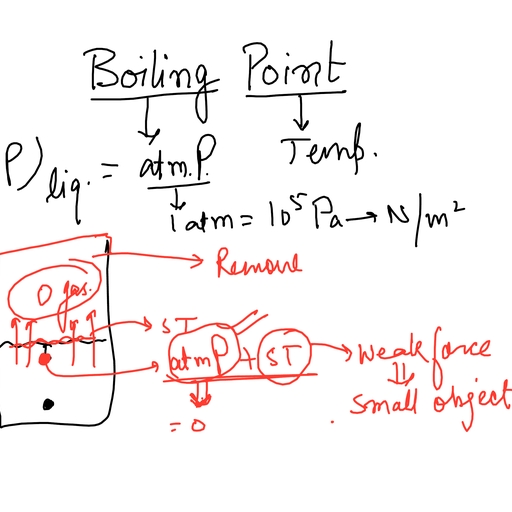
Page 37 :
(ii)Elevation of Boiling point, The boiling point of a liquid is defined as the temperature at which, the vapour pressure of a liquid becomes equal to the atmospheric, pressure.The vapour pressure of a solution is lower than that of, solvent, the solution has to be heated to a high temperature so as to, equalize its vapour pressure with the atmospheric pressure.Thus the, boiling point of the solution will be higher than that of the pure, solvent.The difference between the boiling points of the solution (T b ), and the solvent (T0b) is called the elevation of boiling point. Thus, , ΔTb= Tb -T0b, , Elevation boiling point is directly proportional, to molal concentration of the solute in a solution., ΔTb α m, ,ΔTb = Kb m where ‘Kb’ is called molal elevation constant, or boiling point elevation constant or molal ebullioscopic constant. 37
Page 38 :
From the above equation it is clear that , the elevation, of boiling point depends upon the number of moles of, solute but does not depend upon the nature of the, solute. So it is a colligative property., When molality ,m=1 , ΔTb = Kb, Hence molal elevation constant is defined as the, elevation in boiling point produced for 1 molal solution, (when one mole of non-volatile solute is dissolved per, kilogram(1000g) of solvent).Its unit is K kg mol-1 or K, molal-1, Calculation of molarmass of non-volatile solute, ΔTb = Kb m, , But Molality,m = WB.1000, , MB . W A, ΔTb = Kb WB .1000, MB .WA, , MB =, , Kb xWB x1000, ΔTb xWA, 38
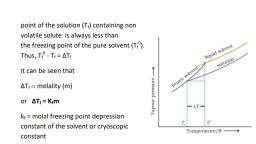
Page 39 :
(ii)DEPRESSION OF FREEZING POINT, The freezing point of a substance is the temperature at which the, solid and liquid phase of the substance have same vapour, pressure.When a non-volatile solute is dissolved in a solvent,its, vapour pressure decreases.Since vapour pressure of the solution is, decreased ,it will become equal to that of the solid solvent at a lower, temperature.It is evident from the figure., , ΔTf = T0f -Tf, Tf0 -freezing point of pure solvent, Tf -freezing point of solution, Depression of freezing point is directly, proportional to molal concentration of, the solute in a solution., ΔT α m, f, , ,ΔT = K m where ‘K ’ is called molal depression constant, f, , f, , f, , or freezing point depression constant or molal cryoscopic constant., 39
Page 40 :
From the above equation it is clear that , the depression, of freezing point depends upon the number of moles of, solute but does not depend upon the nature of the, solute. So it is a colligative property., When molality ,m=1 , ΔT = K, f, , f, , Hence molal depression constant is defined as the, depression of freezing point produced for 1 molal, solution., (when one mole of non-volatile solute is dissolved per, kilogram(1000g) of solvent).Its unit is K kg mol-1 or K, molal-1, Calculation of molarmass of non-volatile solute, ΔTf = Kf m, , But Molality,m = WB.1000, , MB . W A, ΔTf = Kf WB .1000, MB .WA, , MB =, , Kf xWB x1000, ΔTf xWA, , 40