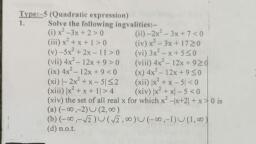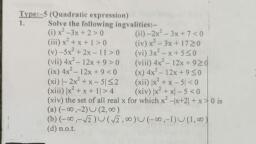Page 1 :
Score, , High, , , , , , Institute, Uth QE. (ALG) Sheet-1, Type-1 4, 1. If the roots of Q. equestion x? - 4x —logsa = 0 are 4. For the equ 3x7 + px + 3 = 0, p> 0 if onc root of, Real then find minimum value of ‘a’? equ is square of the other then ‘p’ is equal to, 1, © 2... . Te the roots of Q..equestion 2x2 - 4x=logiop 30... . ; 5 (0) 1_(e)3 (d)N.O.T.,, are Real then p-maximum is, (2) 100 (b) 10 () 0@)N.O-T. 5. “If the roots of 7 — ax + b= 0 are two consecutive, 7 7 dd integers then a® — 4b is equal to, , 3, fone root of the Q, equestion ix? —2(i + 1) +(2-i) = Ois 8 8, , (2-1) then the other root of equestion is (@)4 @)-4 14 @) N.OT., i (b)2+1 i (d)N.O.T., @i @ 4 @NOF 6. If the roots of x” ~ br + c= 0 are two consecutive, , 4. S.T. the roots of Q.equ a(b—c)x? + b(c—a)x + integers then b’ — 4c is equal to, c(a—b) = 0 are rational where a,b,ceQ ()4 @)-4 © 14 @) N.O.T., , 5. The roots of Q. equ (b+ c— 2a)? + (c +a—2b)i Ts Ifseca & cosec@ are roots of the equx’—px+q=0, Pep ae iiteeshc ones : i then (a) p°= 9(¢ + 2) )p=4a+2, (a) Real (b) Lrrational (c) rational (d) Imaginary @g'=Pet?) (NOT, , 1 8. If sina ee eeawet. ote gxtr=0, 6. If—— is a root of the equx’ + px+qg=0 then (a) p’—q? + 2pr=0 (b)p' +q° + 2pr=0, 5+iv3 “arse @p-¢-2pr=0 NOT., (where p,q€R) then find the value of p&q., Type-4, , * Note:- If a,b,c are odd integer then roots of q. equax’+ Ll. If theQ. equx’—x+3a=Oand 27 -x+a=0, , bx +c=0 can not be rational. have a common root then find the value of ‘a’?, Type-2 2. The value of ‘k’ for which the equ x-ke-21=, , 1 If pr = 2(q +s) then S.T. at least one of equ” — 0 & 2 —3kx+ 35 =0 will have a common root is, px +q=0O and x*—1x+s=0 has real roots where (a) +4 (b+) £1 ©) £3 @O0 (NOT., p.qrseR., , 3. If +3x+5=0& ar +bxtc=O0havea, , 2: P.T. the roots of equ bx” + (b-c)x + (b—c-a)= common root and a,b,cEN then minimum value, O are real & distinct. If the equ ax” + 2bx +b = of a+b +cis equal to, has imaginary root where a,b,ceR. (a)3 (b)6 ()9 @NO.T., , Type-3 4, Ifx taxt+1=0&x't+ar+1=Ohavea, , 1. If the roots of equ px’ + gx tr = 0 are in the ratio common root then, 3:2 then (a) 6p’ = 25gr (b) 67’ = 25pq (a) ac(—-0,-2) (b) ae{-2}, , (c) 6q° = 25pr (d) N.0.T. (c)ac(2,-0) (d)N.O.T., , 2. If one root of the q. equ (/— m)x? + Ix + 1= 0 be 5. Let f(x) = 22 + 5x + 1, if we write f(x) as f(x) =, double the other and ‘/’ is real then find [a(x t 1) (x— 2) + b(x— 2) (x- 1) +e(x—- 1) (+, maximum value of ‘m’. 1)] for real number a, b & c then, , ~ (a) there are infinite nos. of choices for a, b&c, , 3. If one root of the Q. equ ax’ + bx +c =0 is equal (b) only one choice for ‘a’ but infinite nos. of, , a1 choices forb &c, to the n™ power of the other then P.T. (ac")™ + (c) exactly one choice for each a, b &c., (ate) as bo (d) more then one but finite no. of coices for a,b &c., a"c)" =, 6. If the Q. equ. 2x” + 5x + 1, can be written as, , ©

Page 2 :
[a(x + 1) (@— 2) + b(x- 2) (1) te(x- 1), , (x+ 1)] =o for real number a, b & c then, , (a) there are infinite nos. of choices for a, b&c, , (b) only one choice for ‘a’ but infinite nos. of, , choices for b &c, , (c) exactly one choice for each a, b &c., , (d) more then one but finite no. of coices for a,b 4, &e., , If @ & Pare the roots of the Q. equa’ + bx+c=0 :, , * “observe the lists given below’ °° * ‘, List I List II, 1 1, , (A) a=B (1) (ac?)3 + (a?c)} +b=0, (B) @=28 (1) 28 = 9ae, (C) a=3B (3) 8 = 6ac, (D)a=B? (4) 38? = 16ae, , (5)) B= 4acl, , L LS, (6)) (ac*)3+ (a’c)} =, The correct match of List I from List Il is, A B Cc D, , @5 2 4 6, (b)5 2 1 4, (5 2 4 1, (@)N.OT., , , , Page 2

Page 3 :
F Score , Medical | 1IT-JEE 1 X11 XI, , Q.E. (ALG), , , , , ; “, find the equation whose roots be 5 & (-3/2)?, , find the equation whose AM of roots is 8 and, - there G.M. is 52. os SM ah oe SRS, , Find the equation whose sum of roots be 5 and, product of roots be (-3/2)?, , Ifa & Bare the roots of x7 + 5x+4=0 then, , equation whose roots are ——— G42 afi 2, is, (a) 97 4+3x+2=0 (6) 9x7 +3x-2=0, ()9?-3x+2=0 (NOT., , If@ & Bare the roots of equation x —x+1=0, then a+ 6°” is equal to, (@)2 (&)-1(0)1 W@NOT., , Ifa & Bare the roots of equation x —2x+4=0, then the value ofa” + 6" will be, , (a) 2°*" cos(nt/3) —(b) i2"*' sin(n/3), (©) 2 cos(n /3) (@) NOT., Ifa= cos +isin 5 then the Q. equation, , whose roots area=ata?+a'& B=a+a°+, ais (ax +x4+2=0 (b)x¢-x+2=0, ()x?+x-2=0 (d) N.O.T., , Let a & be the roots of equation px” + qx+ r=, , 1, O.If p,q and rare in A.P. and eB 4 then, , ae wl, , , , value of |a@— | is (a), , (©) i (d) N.O.T., , Let p & q be real no. such that p# 0, p’#q and p”, , #~q. Ifa & Bare non zero complex no., satisfyinga + B= p &a’+ f° =q then the Q., equation having a / Band B/ a as its roots is, (a) (p’+q) x7 -{p*-2q)x + (p’ +9) = 0, , () (pq) x7 {p'-2q)x + (p° +q) = 0, , (6) (+9) 7 4p"+2q)x + (p’ +q) = 0, , High, , 10., , 11., , 12., , 13., , 14,, , [TT=JEE | Xt 1 XI, , Sheet-2, , (@) N.O.T., Ifar & Pare the roots of the equation attbxetec, , - 6 (-a, b:#0) the the equation whose roois are" *, , , , , , 1g is (a) ac - bx +1=0, aat+b aB+b, , (b) ae? +hx+1=0 (c)acx*-bx-1=0, (a) N.O.T., , If @, Bare the roots of the equation A (x? — x) +x, +5=0&IfA, & A, are two values of A obtained, , a Fhe 4 Byte, from 3 n3 +t is equal to, pas a, , (a) 4192 (b) 4144 vn @N.O.T., , Ifa & Bare the roots of equar’ + bx t+c=0 &, l-a@ 1-B, , px +qx+r=0 has roots and——— then r, a, , , , may be equal to (a) a + 2b (db)atbte, (0) abe (@) N.O.T., , Leta & Bare the roots of equax’ + bx+c=0&, A=B? -4ac. fa+ B,a?+ B &a'+ B are in, GP. then (a)A #0 (b) bA=0, (c)cA=0 (d) be#0, , nm. P Q, InAPQR, ane afta and tan, are the, , roots of ax’ + bx + c= 0 (a0) then, (a)b=ate (b)c=atb, (c)b =e (dja=b+e, , Type-6 (symmetric function of@ & f), , 1,, , Ifa & Pare the roots of x —ax+b?=0 thena?+, , B’ is equal to (a) a + 287 (b) a? — 287, ()@-26 (@ NOT., , Ifa & Bare the roots of x — 2x +4 =0 then the, value ofr + Bis (a) 32 (b) 128 (c) 56 (d)not., , Ifa & Bare the roots of 2 +3x—4 = 0 then the, , 3, O)-7 ‘, , value of L + i is (a) 3, a Bp 4

Page 4 :
os (@) N.O.T., , 4, If@ & Bare the roots of x7 + 2br +c = 0 then the, , B= cis equal to yea PY (b) eer., , (a-By, 2, , (©) (d) N.O.T., , 5. Tea Baten pty ~Aihenstd, , B, value 28 +o +a “+ BS?, , 6. Ifa + B=-2 &a’+ B =— 56 then Q.equ whose, roots area & Bis (a) x7 +2x-8=0, (be) x7 +2x+8=0 (()7-2x-8=0 (@)N.O.T., , Ti ER Feces es, a, , a 7 +2b, wot, , , , 1, + — is equal to @ 2, &, , © a’ -2b, , , , (d)N.O.T., , Type—7 (symmetric function ofa , 8 & y), 1. Find the cubic equ whose roots are 2,(-3) & 5?, , 2. If @, ,@,,@,,@, are the roots of the equ x‘ +(2V3) x7 + (2-+¥3) = 0 then the value of (1-@,), (-@, \(-@ )(1-@, ) is (@) 1 (6) 4 (©) 5 (d)not, , 3. Ifa ,8& y are the roots of the equx’ + 4x+2=, 0 thena?+ f’+ 7’ is equal to, (a)2 (b)6 (c)-6 (d)N.O.T., , 4, Ifa ,B& y are the roots of the equ’ — 6x° +, 11x+6=0 then a + YBa is equal to, (a) 168 (b)96 (c) 786 (4) N.O.T., , 5s Heng ommiherents ct eet eet, = 0 then value fle, , , , 7 y, 5 @)-1 ©0 @NOT., , x, , IL., , 12., , , , Ifa pay are the roots of the equ’ ~ 20+ 4, \, = 40 then value ofa! "+ Py’ + y'aris, (a)-3 ()-5 (c)-7 (d)N.OT., , Ifa p&y are the roots of the equ 2x’ ~ Ji’ +, 6c + 1= 0 then value ofa? + "+ y’ is equal to, , fe ox (4) NOT., , 4, Ifa, 8 & 7 are the roots of the equ’ + 2x7— 3x, —1=O then value ofa? + 8? + y”7is equal to, (12 &)13. (14 (NOT., , Ifar, B& y are the roots of the equ’ - 3x°+ x, +5=0theny=) a? +afy is satisfies the equ, , (ay +y+2=0 (b)y-y'-y-2=0, ()y +ty-y-3=0 (d)N.O.T., , If xy, x2.) & x4 are roots of the equ x*-’sin2 #, +x'cos2? B-xcos B-sin B= 0 then tan’!x, + tan”, ‘x + tan™lx; + tan’ x, is equal to, , () B w>-s ()-B @NOT., , If the sum of two roots of ° + px’- qx +r=Ois, zero, then pq is (a)-r (b) r (c) 2d (d) N.O.T., , The condition that x’— px’ + gx—r=0 may have, two of its roots equal in magnitude but Opposite, in sign is (a) r= pq (b) r=p"9 (c) r= 4q'p (d), N.O.T., , , , Page xy

Page 5 :
FscoreHigh, , , , , , = 0 has at least one positive root., , , , , , __QE. (ALG) Sheet-3, Type-8 ,, i: Find the Q. equ whose roots are 3 times the roots, of 3ax’ +3bx+c=0 5. If both the roots of the Q. equ? - 2x +P +k =, 5 =O are less than 5, then ‘k’ lics in the interval, + 2... .. Find.the cubi ic equation whose roots cre 4 times. - - (a) £4, 5) (b) 46,9), the roots of x? + 2x?—4x+1=0 (c) (-~,4) (d) N.O.T., 3. Find the equation whose roots is negative to the Type-10, roots of x*— 8x +7=0 1. All the values of m for which both roots of the, equ? -2me+m-1 = 0 are greater than (- 2), 4. Find the equation whose roots is Reciprocal to bat less then (4) lies in the interval, the roots of x?- 8x +7=0 (a)m>3 (b)-l<m<3, ()l<m<4 (d)N.O.T., 5. Find the equation whose roots is twice to the, roots of x*- 8x +7=0 2. If ax (#0) isa root of quar +hx+c=0&, 8(#0) isa root of equ- av +bx+c=0 then, 2n . 4a 6n a, 6. Ifsin sin & sin are the rots of equ? sit. there is a root y of equ gi teErERO, + bx’ + cx+d=0 then find the equ whose roots which is lie bhwar & B., are ease =” cosec— ie ,cOSeC oe 2, é 7 3. Ifa, b,c be real, ifax’ + bx + c= 0 has two real, c, as =+, 7. Ifa, B,yare roots of ° + 4x +1=0 then the roots & B, where a <—16& f > 1, then L +7, 2 2, 2, equ whose roots are a aR ‘i a 2 is equal to, Bry yta arp la, (a) +4x-1=0 (b) xP -4x+1=0 (<0 (b)>0 (c) <0 © (d) NOT, ()x?-4r-1=0 (@) NOT., 8. If @ & @’ are the two imaginary cube roots of, unity then the equ whose roots are ao’& aw, is (a)? t+axrta=0 (b)xe+ar- a=0, (@x-art@=0 (NOT., Type-9, 1. Find the value of ‘a’ for which both the roots of Type=11 2 oe, ako am exceed a 1. Ifx is real , then = — ~*~" takes values in the, x°+2x4+4, 2. Find the value of ‘m’ for which one root of the Interval, equ x*— mx + 1=Ois less then 1 and other is 1, greater then 1. (a) [33] (>) 3, 3) (c) (3,-3) (d)N.O.T., 3. If roots of x°— (a— 3) x + a= 0 are such that at . fe, least one of root is greater than 2 then 2. If x is real, then values of. a 5 lies in the, (aya €[7, 9] (b)a €[7,0] 14 i x +, (c)a €[9,0] @NO.T. interval ofS. ;] (b) (34, . 13 3 13-3, 4." Find the value of ‘a’ for which x°-(a—3)x+a >