Page 1 :
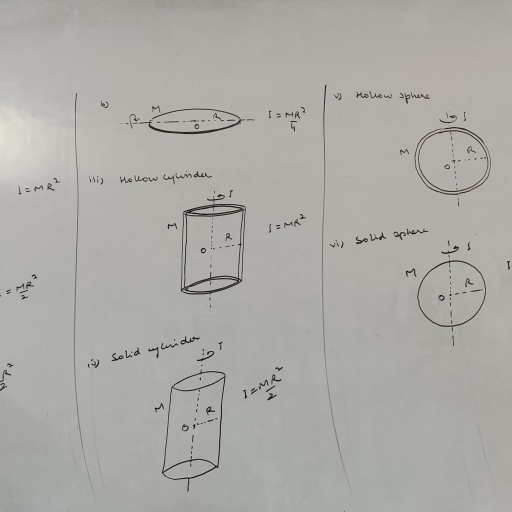
7/52, , ‘PUVA Analogy between line, , 10 Phadecp 4 /Futidaitental Physics svar, , ar motion and rotational motion’, , , , Linear Motion (Fixed Direction), , Rotational Motion (Fixed Axis) ~~ >, , , , 1. Distance/displacement (s), , ds, 2. Lin locity, v= —, inear velocity, a, , 5 . du _d?s, 3. Linear acceleration, a = a = 7, 4. Mass (7m), 5. Linear momentum, p=mv, 6. Force, F=ma, 7. Also, force, F = dp, dt 4, , lf 2, i =>mvu* =-—, 8. Translational K.E 2 om, , 9. Work done, W=F's, 10. Power, P=Fv, , 11. Linear momentum of a system is conserved, when no external force acts on the system., , 12. Work-Kinetic Energy Theorem : W= AK, 13. Equations of Translational motion, , 1, (@v=utat (i) s=utt Sar, , (iii) v?— u? = 2a s, where the symbols have, , their usual meaning., 14. Distance travelled in nth second,, , Spy = 445 nD), , , , 10. Power, P=T@ ui, 11. Angular momentum of a system is conserved ~, , (Principle of conservation of linear momentum), 12. Work-Kinetic Energy Theorem : W= AK, , 13. Equations of Rotational motion, , 14. Angle traced in nth second,, , , , 1. Angle or angular displacement (8), , 2. Angular velocity, O= a, , , , ion gn 20 70" ¥, 3. Angular acceleration, = hi aie :, , 4. Moment of inertia (/) mw OLg, , 5. Angular momentum, L=lo, , 6. Torque, tT=/0, v ie T= ae oy, 7A #0, tora at, 1 P, 8. Rotational K.E = zie =r, 9. Work done, W=7 90 J, , when no external torque acts on the system., (Principle of conservation of angular momentum), , 1, () @) = 0, + at (ii) 0=0, tsar, , , , (iii) ws - a? = 2a 0, where the symbols have, their usual meaning., , Grin = +ZQn-y, , , , , , CENTRE OF MASS, , a, , Formulae used., 1. Position. vector of centre of mass of n Particle, , =n, , « >., system is rol, , , , 2. For two particle system, position vector of centre, , of mass is, , , , To, , 4. If centre of mass lies at the origin,, , 3. The co-ordinates of centre of mass will be, , , , , , xe Mt mtd, mtm, * m, +m, |i, , , , and z= 4% 2p, m +m,, , se y=z=r=0, , , , , , my x) + my x2 =0, xp 4, m, , Scanned with CamScanner, , al

Page 2 :
SYSTEMS OF PARTICLES AND|ROTATIONAL.MOTION, , sito loemy yp ies bas noon, , y =o Citd93, Bh Z i} Mito lane!, , , , ~ Similarly,, , , , ‘and, | \, , | Clearly, the‘algebraic sum of the moments of masses, , , , wWeah ish, a, my, , of various particles about its centre of mass is zero.", , | 5, For a continuous mass distribution,, , 1, . = [Pdn, M, , cm, , 6. Velocity of c.m. of a system of two particles is, , > >, > Mm, Vy + My Vo, cm, , m a my, , “Units used. All masses are in kg, all distances are, , in metre and all velocities in ms!, , , , ‘Example fl Find the centre of mass of a, uniform triangular lamina., NCGERT Solved Example, Solution. In Fig. 7.58, ABC is a uniform, , triangular lamina. It may be subdivided into thin, strips, each parallel to the base BC as shown., , , , FIGURE 7.58, , , , , , , , , , By symmetry, each strip has its centre of mass, at its geometrical centre. If these points are joined,, we get the median AK. Similarly, we can argue that, centre of mass lies on median BL and also on median, CM. It means the centre of mass of uniform triangular, lamina lies at the point of intersection of the three, medians, i.g., on the centroid G of the triangle., , lexamplé Find the centre of mass of, three particles at the vertices of an equilateral, triangle. The masses of the particles are 100 g,, 150 g and 200 g respectively. Each side of the, equilateral triangle is 0.5 m long., , jNCERT}Solved Example, , 7/53, , Solution. Refer to Fig. 7.59,, , FIGURE 7.59, B (0.25, 0.258), , , , , , , , , (0,0) N A, (0.25, 0) (0.5, 0), , , , , , , , In AOBN, cos 60° = ON, _.ON, OB 05, ON = 0-5 cos 60° = 0-25 m, BN _ BN, in 60° = ——=—, ato" OB, 05, , BN = 0-5 sin 60° = 0-5 = =025¥3, .. The co-ordinates of O (0, 0), A (0:5, 0) and B, , (0-25, 0-25 3 ). The masses of 100 g, 150 g and 200 g, are located at the vertices O, A, B of the equilateral, triangle OAB. The co-ordinates of the centre of mass, are, , y bam +My 2 +m, m, +m, +m,, , _100x0-+150% 05+ 200% 0-25, a (100 + 150+ 200), _ 75450 _ 125 _ 5 yy, ~~ 450 450 18, = Nt Ma¥2 + 3%3, , m +m, +m,, 1000 +150%0+ 200%0-25 V3, - 100+150+ 200, , 0, , —=—=m, 450 9 3¥3, Note that the centre of mass C is not the, geometric centre of triangle OAB. This is because, the three vertices of the triangle are not uniformly, loaded., , and Y, , , , eR] Find the position of centre, , ape of the T-shaped plate from O, in Fig., , Scanned with CamScanner

Page 3 :
7154, , , , , , FIGURE 7.60, , fem h, , k—————, 9, , , , , , , , 2, =e, , , , 2., , e-2 Gang, , 6m, , , , , , , , , , 3], , Solution. Suppose 6 is mass per unit area of, , the plate., :. Mass of horizontal portion = 8 x 20 = 160, , Mass of vertical portion = 6 x 20 = 120, Centre of mass O, of horizontal portion is such, that OO, = 1m., Centre of mass O, of vertical portion is such, that OO, = 2+3=5m., If yis distance of cm of T-shaped plate from O,, _ 166x1+126x5 _ 766, “J6o+120 286, , then =2-71m, , example] From a uniform circular disc, of radius R, a circular disc of radius R/6 and, having centre at a distance R/2 from the centre of, the disc is removed. Determine the centre of mass, of remaining portion of the disc., , Solution. Suppose mass per unit area of the disc, is m. Therefore, mass of original disc, , M=nR?xm, Mass of portion removed from the disc, , In Fig. 7.61, mass M is concentrated at O and, mass M’ was concentrated at O’,, , , , FIGURE 7.61, , , , , , , , , , Dhailedhs Ratidaiéntal PhYStes’ (XD kenge,, esta:, , yak, where OO’ = 2", , After the circular disc of mass M’ has been, removed, the disc may be considered as a system of, two masses, M at O and - M’ at O’. If xis the distance, of centre of mass (P) of the remaining part of the disc, , from O, then (91179 HER Rib Ag, _Mx0-M'XR/2 _ M’ eR re, M +(-M’) M -M? 2) 97\09 9), 87 Sad, wR m/36_ RR, “TRm—nR2m/36 2 ~=—70 40, , , , Negative sign shows that P is to the left of 0,, , Example A A circular plate of uniform, thickness has a diameter of 56 cm. A circular, portion of diameter 42 cm is removed from one, edge of the plate. Find centre of mass of the, remaining portion of the disc., , Solution. Here, radius of ciruclar plate, , = = em = 28 cm with centre O. And radius of cir, cular portion removed = = = 21cm with centre O,,, Fig. 7.62., , , , FIGURE 7.62, , , , , , , , , , If m is mass per unit area of disc, then, , M=n (28)? mand m= (21)? m, , Mass of shaded portion,, , m, = M- m, = (m (28)?- 0 (217) m, =343 7m, , If m, and my are assumed to be concentrated at, O, and O, respectively, and O is their centre of mass,, then, , moment of m, about O = moment of m, about 0., my x 0,0 =m, x 0,0, , —, Scanned with CamScanner

Page 4 :
SYSTEMS OF PARTICLES AND ROTATIONAL-MOTION 7/55:, 0,0 =1x0,0 K _ mp R? ith, m, cm | nD = 4, mR? hpxh?, masa ea oma, 344mm 1, toe a ms = 7, This is the distance of c.m. of remaining portion ( oes 3 mre P|, of disc from centre of disc. since, Similarly x.y = 9; Zon = 9, , (example [] Determine the coordinates of, the centre of mass of a right circular solid cone of, base radius R and height h., , Solution. Fig. 7.63 shows a uniform solid cone, of base radius R and height h. It is supposed to be, made up of a large number of circular discs of, different radii and masses., , , , Mee FIGURE 7.63, , (h-y), , h ako wy, , , , Consider one such disc of radius BC = x and, mass dm at a height y from the base., AS ABC and ADO are similar,, , R, 4o_Do ,, 4%, AC. BC x, , h-y, R(h- 2, or xf (i), , , , , , Mass of elementary disc, dm = Volume x density, dm=n2.dyxp, R2(h-yP?, ar, «. Co-ordinates of centre of mass of cone are, , «(ii), , Yom = 5g 7, , ih Ae 1 . npr? -y)?, ti Polisi bpror (h-y)* dy, , 2:5, BPR’ fenry+y? 2h? )ay, 0, , Hence co-ordinates of the centre of mass of solid, , h, cone are ( ? 0}, , Example] A man of mass m, is standing, on a platform of mass m, kept on a smooth, horizontal surface. It the man moves a distance d, wnt, the platform, find the displacement of the, platform w.r.t., ground., , Solution. Here, mass of man = my,, mass of platform = m,, , , , FIGURE 7.64, m4,, , | m, , eer TTT, , As the surface on which platform is placed is, smooth, therefore no external force is acting along, the horizontal, i.e.,, , , , , , , , 4 2, Foxy, =0, Therefore, O.., = 0 and Ug, = const., , > nae s, :, ASU, 18 ZerO initially, it would remain zero, , even after the man moves. Refer to Fig. 7.64., Let x; = displacement of man towards right, displacement of platform towards left, my X=) XQ, xy, +x,=d, , y=, , and, , m*2 tx, =d, im,, , , , , , Scanned with CamScanner

Page 5 :
7156, , HagroRQuE, POWER OF TORQUE,, Tl)" WORK DONE BY TORQUE AND, ANGULAR MOMENTUM, , Formula used, , 1. Torque = force x its perpendicular distance from, the axis of rotation, , ,» 320?, 2. Torque, t= rF sin® or T= rXF, 3, Power of torque, P=T@, 4. Work done by torque, W=1 0, 5. Angular momentum = Linear momentum x its, perpendicular distance from the axis of rotation, 6. Angular momentum,, , 4 7a 4 8, L=rpsin® or L=rxp., , 7, When a particle of mass m is moving with a ., , uniform speed v along a circle of radius r ;, L=mur. ‘, , 8. Torque = rate of change’ of angular momentum, tadl/dt, , Units used. Torque is in N-m, work done in joule,, , power in watt, angle in radian, angular velocity in, , . Tadian/sec., Mass in kg, linear velocity v in m/s and, angular momentum L in kg m? s~!., , , , fexamplef] Find the torque of a force, , (5 je 2j+ 3k) about the origin ; which acts on, A A A, , a particle whose position vector is (i — j+k)., Solution. Here,, , > A A A 3D ACA A, F =(5i-2j+3k) and rp =(i-j+k), 3 34° AAA A A ON, T= 7rxF =(i-j+k)x(5i-2j+3k), A A A, i jk, =|1 -1 1, 523, , A A A, = i(-3+2)— j(3-5)+k(-2+5), An A A, =(-i+2j+3k), \Exampref] 4 torque of 10° N-m acting on, a rigid body, turns it through 30° in 0-2 second., , Calculate work done by the torque on the body, and power of torque., , Solution. Here, t = 103 N-m,, , 6 =30° =f radian, t= 0-2 s., , att<, , 1011 Phaidasp 4 Fiinidaiterital Physics CRI), , % asuincee, =10=10 x= FS S—x108, a a, = 5.23 x 107 J |, puqism lng SOMO. rain, iene amie Laie 5 x 103 watt, , Example [ll] A constant torque is acting on, a wheel. If starting from rest, the wheel makes n, rotations in t seconds, show that ‘the angular, , giotviodt, , eather 4nn f, acceleration is given by o = a rad s~2,, , , , , , Solution. Here, ®) =0,0=2 11 radian, ty,, t=t,0=?, , 12, As O=aytt> a, , 1 2, 2nn=0+- at, mn 2, , 4nn, a =— rads?, , t?, (Example [§l Show that angular momen, tum of a satellite of mass M, revolving around, earth of mass M, in an orbit of radius r is, , GM? M,r., , Solution. A satellite revolves around earth under, , gravitational pull which provides the necessary, centripetal force,, , , v2 GM,M, Le, M —=—*&—+, s r r2, v= GM,, , , , e, Angular momentum of satellite L = M,-v-r, , GM, L=M,4 £xr, r, , = {em2M_r, , \Exampre[¥] A small particle of mass m is, , , , projected at an angle @ with x-axis with initial, velocity vg in x-y plane as shown in Fig. 7.65., Calculate the angular momentum of the particle, , vp sin®, ge, , , , Scanned with CamScanner