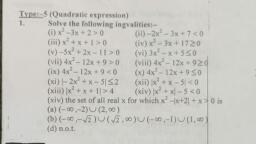Page 1 :
MATHEMATICAL TOOLS, , LOGARITHM, Logarithm of a number (a) to some base (x) is that number (b) which when raised to the base gives that, number., ���� a = b  �� = �, , Two bases are in common use � = 2.71828 (exponential) and 10. Logarithm to base e is called natural, logarithm and is denoted as loge or ln. Logarithm to base 10 is called decimal logarithm and is denoted as, log10, Formulae (applicable to all bases), (1) log ab = log a + log b, (3) log, , �, �, , log10 e = 0.434294, , = log a – log b, , loge10 = 2.30259, , (3) log ab = b log a, , log10 2 = 0.303, , (4) logx a = logya logxy, (5) log 1= 0, Decimal logarithm, log10 1 = 0  100 = 1, log10 10 = 1  101 = 10, log10 100 = 2  102 = 100, log101000 = 3  103 = 1000, , and so on., , Logarithm of a number between 1 and 10 lies between 0 and 1, logarithm of numbers between 10 and 100, lies between 1 and 2 and so on., Logarithm of a number therefore has an integral and a fractional part. The integral part is called, characteristic and is determined by counting number of digits in number (-1) before decimal. The fractional, part is called mantissa and is determined using table., , A-13, Second Floor, Prashant Vihar, Delhi, Contacts: 9999553673

Page 2 :
MATHEMATICAL TOOLS, , 1., , sin =, cos =, , 2., 3., , 4., , 5., , p, , h, b, , h, p, , =, , =, , TRIGONOMETRY, , 1, , cosec θ, 1, , secθ, sinθ, , tan  = b = cos θ =, , 1, , cotθ, , sin2  + cos2  =1, sec2  - tan2  =1, cosec2  - cot2  = 1, sin(A  B) = sin A cos B  cos A sin B, cos (A  B) = cos A cos  B sin A sin B, tan � ±tan �, tan (A  B ) = 1∓tan � sin �, , sin 2 = 2 sin cos, cos 2 = cos2 - sin2 = 2 cos2  - 1 = 1 - 2 sin2., 2tanθ, tan 2 = 1−tan2θ, sin 3 = 3sin - 4sin3, cos 3 = 4cos3 – 3cos, �+�, �−�, sin C + sin D = 2 sin 2 cos 2, 2+�, , sin C - sin D = 2cos, cos C + D = 2 cos, 6., 7., , 2, �+�, 2, , cos C – cos D = 2 sin, sin −� =− ����, cos −� = ����, , sin, , cos, , �+�, 2, , sin (+ ve), cos (– ve), tan ( –ve ), , 2, �−�, 2, , sin, , �−�, 2, , All ( + ve), , sin ( –ve ), cos ( –ve ), tan ( + ve ), 8., , �−�, , sin ( –ve ), cos ( +ve), tan ( –ve ), , sin (90-) = cos , sin (90+) = cos, cos (90+) = - sin , , cos (90+) = - sin , cos (90-) = sin , sin(180-) = sin, , cos (180-) = - cos, sin(180+) = - sin, cos(180+) = - cos, , 9., , , sin , , 00, 0, , cos, , 1, , sin 37 , 0, , 300, , 1, 2, 3, 2, , 3, 0,  cos 53, 5, , 450, , 600, , 1, 2, 1, 2, cos 3 7, , 0, , 900, 1, , 3, 2, 1, 2, 4, ,  s in, 5, , 0, , 53, , 1200, , 1350, , 3, 2, 1, , 2, , 1, , 0, , A-13, Second Floor, Prashant Vihar, Delhi, Contacts: 9999553673, , 2, 1, 2, , 1500, , 1, 2,  3, 2, , 1800, 0, -1

Page 3 :
MATHEMATICAL TOOLS, , ALGEBRA, (a + b) 2 = a 2 + b 2 + 2ab = (a - b) 2 + 4ab, (a - b) 2 = a 2 + b 2 - 2ab = (a + b )2 - 4ab, (a + b) 3 = a 3 + b 3 + 3a 2 b + 3ab 2, (a - b) 3 = a 3 – b 3 + 3ab 2 - 3a 2 b, , n(n  1), 2, n, (, n,  1)(2 n  1), n2 =, 6, 2, n (n  1)2, 3, n =, 4, n =, , BINOMIAL THEOREM / APPROXIMATION, , (1 = �)� = 1 + �� +, , � �−1, 2, , x2 +, , � �−1 �−2, 3, , �3 + …, , If x ≪ 1 higher powers of x are negligibly small and hence can be neglected and, , (1 + �)� = 1 + ��, , QUADRATIC EQUATION, ax 2 + bx + c = 0, Roots / solutions of this equation are:,  ,  , , b , , b2  4ac, 2a, , b , , b2  4ac, 2a, , Here,, D=, If,, D0, D=0, D<0, Also, , b 2  4ac = Discriminant, Roots are real and unequal, Roots are real and equal, Roots are imaginary, �, , +=−�, , �, ,  = �, , and, x 2 - ( + ) x +  = 0, , A-13, Second Floor, Prashant Vihar, Delhi, Contacts: 9999553673

Page 4 :
MATHEMATICAL TOOLS, , COORDINATE GEOMETRY, (1) x and y are cartesian coordinates of position of P., , , , OP = position vector of P  r, , r = OP,  = angle that OP makes with + x axis., �, � are polar coordinates of position of P., , r  x 2  y 2 ���� = ��, , � = � ����, , � = � sin �, , � = � cos �, , r  x2  y 2  z 2, , (2) x, y, z are cartesian coordinates of position of P., �� =Position vector of P., (�, �, �, �) are polar coordinate of P., y = r cos , z = r cos , Direction cosines of ��, �, ��� � = = �, ��, ���� = = �, �, �, , cos  = = �, �, �2 + �2 + �2 = 1, (3) Distance between two points �(x1, y1, z1,) ��� � �2 , �2 , �2, �� = √(�� − �� )� + (�� − �� )� + (�� + �� )�, , A-13, Second Floor, Prashant Vihar, Delhi, Contacts: 9999553673

Page 5 :
MATHEMATICAL TOOLS, , Straight line, , GRAPHS, , Linear equations in x and y represent a straight line. Equation of a straight line is, y = mx + c., c = Intercept on y axis (if x = 0 y = c), m = slope of line = tan.,  = Angle made by the line with + x axis., m determines slant of the line. It also determines rate of change of y with x., (i) m = + ve, c=0, , (ii) m = + ve, c = + ve, , (iii) m = + ve, c = - ve, , (iv) m = tan  = - tan = - ve, c = + ve, , .., , (v) m = - ve, c = - ve, , (vi) m = -ve, c=0, , (vii) m = 0, c = + ve, , (viii) m = 0, c = - ve, , A-13, Second Floor, Prashant Vihar, Delhi, Contacts: 9999553673

Page 6 :
MATHEMATICAL TOOLS, , Circle, Equation of a circle with centre at origin, x2 + y2 = R 2, , Equation of circle with centre at (x1, y1), (� − �1 )2 + (� − �1 )2 = �2, � = ������ �� ������, Parabola, Quadratic equations represent parabolic curves., (i) � = ��2 + �, , (ii) � = ��2, , (iii) � = ��2 + �, , (iv) � = ��2, , (v) � = �� − ��2, , A-13, Second Floor, Prashant Vihar, Delhi, Contacts: 9999553673

Page 7 :
MATHEMATICAL TOOLS, , Hyperbola, Inverse proportioanalities represent hyperbola., 1, , (i) � = �, , 1, , (ii) � = �2, , Ellipse, Ellipse is represented by the equation of the form, �2, , �2, , +, , �2, �2, , = 1 Where,, , a = semi major axis, b = semi minor axis of the ellipse, and O is one of the focii of the ellipse., Eccentricity of ellipse is, , Other Important graphs, , (i) � = ����, (Sinusoidal), , �=, , �2 − �2, �2, , (ii) � = cos �, , (iii) � = tan �, , A-13, Second Floor, Prashant Vihar, Delhi, Contacts: 9999553673

Page 8 :
MATHEMATICAL TOOLS, , CALCULUS, Quantities are of two kinds:, (i) Constants : quantities whose values do not change. Quantities which always take one and same value., eg - G, g, c etc., (ii)Variables : quantities whose values change. Quantities which can take any value from a set of many, values., Variables are of two kinds:, (a) Independent variables - Variables which can be assigned any value from a set of many values, (b) Dependent variables - Variables which take a value from a set of many values depending on value, assigned to independent variables., Example, Cost = Rate x number, Rate is constant, Number is independent Variable, Cost is dependent variable, Function: Relation between variables is called a function. If two variables x and y are so related that for, every value of x there is a value of y (i.e if x is assigned a value, y takes a value) then y is said to be a, function of x. Expressed as:, �=� �, Read as: y is a function of x., In such a function x is independent and y is dependent variable., Different functions are also represented as,, �=� �, � = ℎ(�), Limiting Value, Mathematically, , o, , 0, , O ,  ,  ....etc are undefined. They are called indeterminate forms., o, , To define values of such functions we find their limiting value., Let y  f  x , , x  a , y is defined. Also as x  a y  b then b is said to be the, limiting value of y as x approaches a  or at x  a , At x  a , y is indeterminate, but if, , Thus limiting value of a function is the value to which function approaches., Written as, , Lt, yb, xa, , If function is undefined its limiting value is taken to be its defined value., If function is defined actual value is taken to be its limiting value., Eg., , y, , x2  4, x2, , if x  2, , y, , 0, 0, , Undefined but if x  2, , y, , 0, 0, , defined, , y  4. 4 is then said to be the limting value of y as x approaches 2., Also rationalizing , y  x  2 and if x  2 , y = 4., As x  2, , A-13, Second Floor, Prashant Vihar, Delhi, Contacts: 9999553673

Page 9 :
MATHEMATICAL TOOLS, , Differentiation, , Suppose y  f  x  ., If the value of independent variable x changes by x , dependent variable y also changes correspondingly, by y., , y  y  f  x  x , , Change in y is then ,, , y  f  x  x   f  x , , Rate of change of y with x is, , y f  x  x   f  x , , x, x, Taking limiting value as x  0, f  x  x   f  x , Lt, y Lt, , x., x  0 x x  0, We define, , Lt, y dy, ,  Derivative of y w.r.to x = Differential coefficient of y with respect to x., x  0 x dx, f  x  x   f  x , dy Lt, y Lt, , , x, dx x  0 x x  0, , Alternatively,, , y  f x, , Change in y = y, change in x = x, small change in y = y, small change in x = x, Infinitely small change in y = dy Infinitely small change in x = dx, The ratio, , dy, is defined as the derivative of y w.r.to x or differential coefficient of y w.r.to x., dx, , In can be treated as:, (i)Ratio of infintesimal change in y and x., (ii)Rate of change of y with x., Examples, (i) y, ,  sin x, , Lt sin  x  x   sin x, Lt 2 cos  x  x / 2 sin x / 2, dy, , , x  0, dx x  0, x, x, Lt, sin x / 2, , cos  x   x ,  cosx, x  0, x / 2, , (ii), , y  x2, , Lt, Lt  x  x   x 2, Lt x 2  x 2  2 xx  x 2, dy, , 2 x  x  2 x., , , x  0, x  0, dx x  0, x, x, 2, , A-13, Second Floor, Prashant Vihar, Delhi, Contacts: 9999553673

Page 11 :
MATHEMATICAL TOOLS, , Applications, (i)Rate measurer:, (ii), , dy, = Instantaneous rate of change of y with x., dx, , dy,  Ratio of infinitesimal changes in y and x., dx, , (iii) Slope of curve:, , y  f x, , dy,  slope of the curve represented by y  f  x , dx, , (iv) Maxima and minima:, , y  f x, To find maximum/ minimum value of y and values of x at which y would be maximum or, minimum, , dy, dx, dy, dy, (ii) Set, = 0 [when y = maximum/ minimum,,  0 ] to find an equation in x., dx, dx, (i) Find, , (iii) Solve this equation to find values of x. Let these values be a, b …… At these values of x, , dy,  0 and y will be minimum or miximum., dx, d2y, d  dy  d 2 y, . Put x  a in 2 ., (iv) Find,  , dx, dx  dx  dx 2, d2y,  0 at x = a, y is maximum., If, dx 2, If, , d2y,  0 at x = a, y is minimum., dx 2, , A-13, Second Floor, Prashant Vihar, Delhi, Contacts: 9999553673

Page 12 :
MATHEMATICAL TOOLS, , Indefinite Integration, , Integration is inverse of dfferentiation., If differential coefficient of f(x) with respect to x be F(x), , d, f  x  F  x, dx, , then integral of F(x) with respect to x would be f(x)., ,  F  x  dx  f  x , Identities, , F  x, ,  F  x  dx  f  x , , cos x, sin x, sec2 x, sec x tan x, cos ec x cot x, , sin x, - cos x, tan x, , cos ec 2 x, , - cots, , Also., ,  cos n x dx , , Sec x., - cosecx, , nx,  e dx , , enx, n, , sin x, n, , nn1, n 1, ex, log x., , x  n  1, n, , ex, 1, x, ax, , ax, log e a, , Formula / Methods of integration, , , (ii)   u  v  dx   udx   vdx, (i) dx  x, , , , , , , ,  du, , , , , , (iii) uvdx  u vdx ,  dx vdx  dx ., (iv) If the function to be integrated is not in standard form we can reduce it to standard form using some, mathematical identity and then intgrate., (v) Integration by substitution: Function can also be reduced into standard form using some proper, substitution. When we replace function by some other function of a different variable the variable of, integration is also replaced by same variable., , A-13, Second Floor, Prashant Vihar, Delhi, Contacts: 9999553673

Page 13 :
MATHEMATICAL TOOLS, , Definite integration, , Integration of F(x) as x varies from a to b is called definite integral of F(x) between a and b, If,, ,  F  x  dx  f  x , Then definite integral of f(x) between a and b is,, , , , b, a, , b, , F  x  dx   f  x    f  b   f  a , a, , Applications, (1) Definite integral is the limiting value of a sum., (2) Definite integral of F(x) between a and b is equal to area under the curve y = F(x) and x axis between, x = a and x = b., , A-13, Second Floor, Prashant Vihar, Delhi, Contacts: 9999553673